Курсовая работа: Емкость резкого p-n перехода
ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра микроэлектроники
![]()
Курсовая работа
по курсу ФОМ
Тема
Емкость резкого p-n перехода
г. Пенза, 2005 г.
Содержание
Задание
Обозначение основных величин
Основная часть
1. Расчет собственной концентрации электронов и дырок
2. Расчет контактной разности потенциалов
3. Расчет толщины слоя объемного заряда
4. Расчет барьерной емкости
Список используемой литературы
Задание
1. Вывести выражение для емкости резкого p-n перехода в случае полностью ионизированных примесей
2. Рассчитать величину барьерной емкости резкого p-n перехода при 300 К и напряжении V. Считать что примеси полностью истощены, а собственная проводимость еще очень мала.
3. Построить график зависимости барьерной емкости от температуры.
4. Составить программу вычисления значений барьерной емкости для графика.
| Полупроводник | Ge |
| V ,В | 0 |
|
Nd ,см |
1,0 |
|
Na ,см |
1,0 |
|
S ,мм |
0,15 |
Обозначение основных величин
DE – ширина запрещенной зоны.
[DE] =1,8![]() 10
10![]() Дж=1,13 эВ.
Дж=1,13 эВ.
e![]() – электрическая постоянная.
– электрическая постоянная.
e![]() =8,86
=8,86![]() 10
10![]()
![]() .
.
![]() – подвижность электронов.
– подвижность электронов.
[![]() ]=0,14 м
]=0,14 м![]() /(В
/(В![]() с)
с)
![]() – подвижность дырок.
– подвижность дырок.
[![]() ]=0,05 м
]=0,05 м![]() /(В
/(В![]() с)
с)
m![]() – эффективная масса электрона.
– эффективная масса электрона.
m![]() =0,33
=0,33![]() m
m![]() =0,33
=0,33![]() 9,1
9,1![]() 10
10![]() =3,003
=3,003![]() 10
10![]() кг
кг
m![]() – эффективная масса дырки.
– эффективная масса дырки.
m![]() =0,55
=0,55![]() m
m![]() =0,55
=0,55![]() 9,1
9,1![]() 10
10![]() =5,005
=5,005![]() 10
10![]() кг
кг
m![]() – масса покоя электрона.
– масса покоя электрона.
m![]() =9,1
=9,1![]() 10
10![]() кг.
кг.
![]()
![]() – время релаксации электрона.
– время релаксации электрона.
![]()
![]() =2
=2![]() 10
10![]() с.
с.
![]()
![]() – время релаксации дырки.
– время релаксации дырки.
![]()
![]() =10
=10![]() с.
с.
S – площадь p-n перехода.
[S]= 10![]() мм
мм![]()
n![]() – собственная концентрация
электронов.
– собственная концентрация
электронов.
[n![]() ]=м
]=м![]()
p![]() – собственная концентрация дырок.
– собственная концентрация дырок.
[p![]() ]=м
]=м![]()
![]()
N![]() – эффективное число состояний в зоне
проводимости, приведенное ко дну зоны.
– эффективное число состояний в зоне
проводимости, приведенное ко дну зоны.
[N![]() ]=м
]=м![]()
N![]() – эффективное число состояний в
валентной зоне, приведенное к потолку зоны.
– эффективное число состояний в
валентной зоне, приведенное к потолку зоны.
[N![]() ]=м
]=м![]()
k – константа Больцмана.
k = 1,38![]() 10
10![]()
![]() .
.
Т – температура.
[T]=K.
![]() - число Пи.
- число Пи.
![]() =3,14.
=3,14.
h – константа Планка.
h = 6,63![]() 10
10![]() Дж
Дж![]() с.
с.
V![]() –контактная разность потенциалов.
–контактная разность потенциалов.
[V![]() ]=B.
]=B.
j![]() – потенциальный барьер.
– потенциальный барьер.
[j![]() ]=Дж или эВ.
]=Дж или эВ.
q – заряд электрона.
q=1,6![]() 10
10![]() Кл.
Кл.
n![]() – концентрация донорных атомов в n-области.
– концентрация донорных атомов в n-области.
[n![]() ]=[N
]=[N![]() ]=2,0
]=2,0![]() 10
10![]() м
м![]()
p![]() – концентрация акцепторных атомов в p-области.
– концентрация акцепторных атомов в p-области.
[p![]() ]=[N
]=[N![]() ]=9,0
]=9,0![]() 10
10![]() м
м![]()
e – диэлектрическая проницаемость.
e=15,4
d – толщина слоя объемного заряда.
[d]=м.
N![]() – концентрация акцепторов.
– концентрация акцепторов.
[N![]() ]=1,0
]=1,0![]() 10
10![]() см
см![]()
N![]() – концентрация доноров.
– концентрация доноров.
[N![]() ]=1,0
]=1,0![]() 10
10![]() см
см![]()
V – напряжение.
[V]=0 В.
C![]() – барьерная емкость.
– барьерная емкость.
[C![]() ]=Ф.
]=Ф.
![]() – удельная барьерная емкость.
– удельная барьерная емкость.
[![]() ]= Ф/м
]= Ф/м![]()
m![]() – уровень Ферми.
– уровень Ферми.
[m![]() ]=Дж или эВ.
]=Дж или эВ.
1. Расчет собственной концентрации электронов и дырок
![]() Е Е+dЕ
Е Е+dЕ
![]()
![]()
![]()
![]() Зона проводимости
Зона проводимости
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Е
Е
![]()
![]()
0
![]()
![]()
![]() Е
Е![]()
- m
![]()
![]()
![]() Е
Е![]()
![]() -m¢
-m¢
Е![]()
Валентная зона.
Рис.1.Положение уровня Ферми в невырожденном полупроводнике.
На рис. 1 показана зонная
структура невырожденного полупроводника. За нулевой уровень отсчета энергии
принимают обычно дно зоны проводимости Е![]() . Так как для невырожденного газа
уровень Ферми m должен
располагаться ниже этого уровня, т.е. в запрещенной зоне, то m является величиной отрицательной (-m >>kT). При температуре Т, отличной от абсолютного нуля, в зоне
проводимости находятся электроны, в валентной зоне – дырки. Обозначим их
концентрацию соответственно через n и p. Выделим около дна зоны проводимости
узкий интервал энергий dЕ,
заключенный между Е и Е+dЕ.
Так как электронный газ в полупроводнике является невырожденным, то число электронов
dn, заполняющих интервал энергии dЕ (в расчете на единицу объема
полупроводника), можно определить, воспользовавшись формулой :
. Так как для невырожденного газа
уровень Ферми m должен
располагаться ниже этого уровня, т.е. в запрещенной зоне, то m является величиной отрицательной (-m >>kT). При температуре Т, отличной от абсолютного нуля, в зоне
проводимости находятся электроны, в валентной зоне – дырки. Обозначим их
концентрацию соответственно через n и p. Выделим около дна зоны проводимости
узкий интервал энергий dЕ,
заключенный между Е и Е+dЕ.
Так как электронный газ в полупроводнике является невырожденным, то число электронов
dn, заполняющих интервал энергии dЕ (в расчете на единицу объема
полупроводника), можно определить, воспользовавшись формулой :
N(E)dE=![]() (2m)
(2m)![]() e
e![]() E
E![]() dE
dE
dn=![]() (2m
(2m![]() )
)![]() e
e![]() e
e![]() E
E![]() dE
dE
где m – эффективная масса электронов, располагающихся у дна зоны проводимости.
Обозначим расстояние от дна зоны проводимости до уровня Ферми через -m, а от уровня Ферми до потолка валентной зоны через -m¢. Из рис. 1 видно, что
m+m¢=-E![]() ,
,
m¢=-(Е![]() +m)
+m)
где Е![]() (
(![]() Е) - ширина запрещенной
зоны.
Е) - ширина запрещенной
зоны.
E![]() =Е +bТ
=Е +bТ
Полное число электронов n, находящихся при температуре Т в
зоне проводимости, получим, интегрируя (1.2) по всем энергиям зоны
проводимости, т.е. в пределах от 0 до Е![]() :
:
n=4![]()
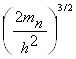
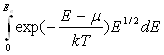
Так как с ростом Е функция exp(-E/kT) спадает очень быстро, то верхний предел можно заменить на бесконечность:
n=4![]()

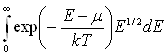
Вычисление этого интеграла приводит к следующему результату:
n=2 exp
exp ![]() (1.5)
(1.5)
Введем обозначение
N![]() =2(2
=2(2![]() m
m![]() kT/h
kT/h![]() )
)![]() (1.6)
(1.6)
Тогда (1.5) примет следующий вид:
n=N![]() exp(
exp(![]() /kT)
(1.7)
/kT)
(1.7)
Множитель N![]() в (1.7) называют эффективным числом состояний в зоне
проводимости, приведенным ко дну зоны. Смысл этого числа состоит в следующем.
Если с дном зоны проводимости, для которой Е=0, совместить N
в (1.7) называют эффективным числом состояний в зоне
проводимости, приведенным ко дну зоны. Смысл этого числа состоит в следующем.
Если с дном зоны проводимости, для которой Е=0, совместить N![]() состояний, то, умножив это число на вероятность
заполнения дна зоны, равную f
состояний, то, умножив это число на вероятность
заполнения дна зоны, равную f![]() (0)=exp(
(0)=exp(![]() /kT),
получим концентрацию электронов в этой зоне.
/kT),
получим концентрацию электронов в этой зоне.
Подобный расчет, проведенный для дырок, возникающих в валентной зоне, приводит к выражению:
p=2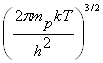 exp
exp![]() =N
=N![]() exp
exp![]() = N
= N![]() exp
exp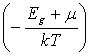 (1.8)
(1.8)
где
N![]() =2
=2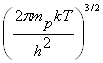 (1.9)
(1.9)
– эффективное число состояний в валентной зоне, приведенное к потолку зоны.
Из формул (1.7) и (1.8) следует, что концентрация свободных носителей заряда в данной зоне определяется расстоянием этой зоны от уровня Ферми: чем больше это расстояние, тем ниже концентрация носителей, так как m и m¢ отрицательны.
В собственных
полупроводниках концентрация электронов в зоне проводимости n![]() равна концентрации дырок в валентной зоне p
равна концентрации дырок в валентной зоне p![]() , так как
, так как
каждый электрон, переходящий в зону проводимости, «оставляет» в валентной зоне после своего ухода дырку. Приравнивая правые части соотношения (1.5) и (1.8), находим
2 exp
exp ![]() =2
=2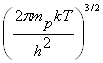 exp
exp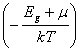
Решая это уравнение относительно m, получаем
m![]() = -
= -![]() +
+![]() kT ln
kT ln![]() (1.10)
(1.10)
Подставив m![]() из (1.10) в (1.5) и (1.7), получим
из (1.10) в (1.5) и (1.7), получим
n![]() =p
=p![]() =2
=2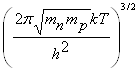 exp
exp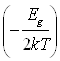 =(N
=(N![]() N
N![]() )
)![]() exp
exp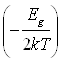 (1.11)
(1.11)
Из формулы (6.12) видно,
что равновесная концентрация носителей заряда в собственном полупроводнике
определяется шириной запрещенной зоны и температурой. Причем зависимость n![]() и p
и p![]() от этих параметров является очень резкой.
от этих параметров является очень резкой.
Рассчитаем собственную концентрацию электронов и дырок при Т=300К.
Eg=(0,782-3,9![]() 10
10![]()
![]() 300)1,6 10-19
=1,064
300)1,6 10-19
=1,064![]() 10-19
Дж
10-19
Дж
N![]() =2(2
=2(2![]() m
m![]() kT/h
kT/h![]() )
)![]() =2
=2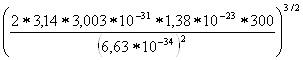 =2
=2![]() = =2
= =2![]() =4,7
=4,7![]() 10
10![]() (см
(см![]() )
)
N![]() =2
=2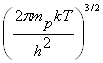 =2
=2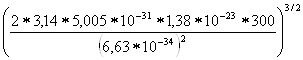 =2
=2![]() =10,2
=10,2![]() 10
10![]() (см
(см![]() )
)
n![]() =p
=p![]() =(N
=(N![]() N
N![]() )
)![]() exp
exp![]() =
=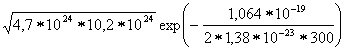 =
=
6,92![]() 10
10![]()
![]() 2
2![]() 10
10![]() =13,8
=13,8![]() 10
10![]() (см
(см![]() )
)
2. Расчет контактной разности потенциалов
Для n-области основными носителями
являются электроны, для p-области
– дырки. Основные носители возникают почти целиком вследствие ионизации
донорных и акцепторных примесей. При не слишком низких температурах эти примеси
ионизированы практически полностью, вследствие чего концентрацию электронов в n-области n![]() можно считать равной концентрации донорных атомов: n
можно считать равной концентрации донорных атомов: n![]() »N
»N![]() , а концентрацию дырок в p-области p
, а концентрацию дырок в p-области p![]() – концентрация акцепторных атомов в p-области: p
– концентрация акцепторных атомов в p-области: p![]() »N
»N![]() .
.
Помимо основных носителей
эти области содержат не основные носители: n-область – дырки (p![]() ), p-область
– электроны (n
), p-область
– электроны (n![]() ). Их концентрацию можно определить,
пользуясь законом действующих масс:
). Их концентрацию можно определить,
пользуясь законом действующих масс:
n![]() p
p![]() = p
= p![]() n
n![]() =n
=n![]() .
.
Как видим, концентрация дырок в p-области на 6 порядков выше концентрации их в n-области, точно так же концентрация электронов в n-области на 6 порядков выше их концентрации в p-области. Такое различие в концентрации однотипных носителей в контактирующих областях полупроводника приводит к возникновению диффузионных потоков электронов из n-области в p-область и дырок из p-области в n-область. При этом электроны, перешедшие из n- в p-область, рекомбинируют вблизи границы раздела этих областей с дырками p-области, точно так же дырки, перешедшие из p- в n-область, рекомбинируют здесьс электронами этой области. В результате этого в приконтактном слое n-области практически не остается свободных электронов и в нем формируется неподвижный объемный положительный заряд ионизированных доноров. В приконтактном слое p-области практически не остается дырок и в нем формируется неподвижный объемный отрицательный заряд ионизированных акцепторов.
Неподвижные объемные
заряды создают в p–n-переходе контактное электрическое
поле с разностью потенциалов V![]() ,
локализованное в области перехода и практически не выходящее за его пределы.
Поэтому вне этого слоя, где поля нет, свободные носители заряда движутся
по-прежнему хаотично и число носителей, ежесекундно наталкивающихся на слой
объемного заряда, зависит только от их концентрации и скорости теплового
движения. Как следует из кинетической теории газов, для частиц, подчиняющихся классической
статистике Максвела–Больцмана, это число nопределяется следующим соотношением:
,
локализованное в области перехода и практически не выходящее за его пределы.
Поэтому вне этого слоя, где поля нет, свободные носители заряда движутся
по-прежнему хаотично и число носителей, ежесекундно наталкивающихся на слой
объемного заряда, зависит только от их концентрации и скорости теплового
движения. Как следует из кинетической теории газов, для частиц, подчиняющихся классической
статистике Максвела–Больцмана, это число nопределяется следующим соотношением:
n=![]() n
n![]() S, (2.1)
S, (2.1)
где n![]() - концентрация частиц;
- концентрация частиц;![]() - средняя скорость теплового
движения; S – площадь, на которую они падают.
- средняя скорость теплового
движения; S – площадь, на которую они падают.
Неосновные носители –
электроны из p-области и дырки из n-области, попадая в слой объемного
заряда, подхватываются контактным полем V![]() и переносятся через p–n-переход.
и переносятся через p–n-переход.
Обозначим поток
электронов, переходящих из p- в n-область, через n![]() , поток дырок, переходящих из n- в p-область, через p
, поток дырок, переходящих из n- в p-область, через p![]() .
.
Согласно (2.1) имеем
n![]() =
=![]() n
n![]()
![]()
![]() S, (2.2)
S, (2.2)
p![]() =
=![]() p
p![]()
![]()
![]() S. (2.3)
S. (2.3)
Иные условия складываются
для основных носителей. При переходе из одной области в другую они должны
преодолевать потенциальный барьер высотой qV![]() , сформировавшийся в p–n-переходе. Для этого они должны обладать кинетической
энергией движения вдоль оси c, не меньшей qV
, сформировавшийся в p–n-переходе. Для этого они должны обладать кинетической
энергией движения вдоль оси c, не меньшей qV![]() . Согласно
(2.1) к p–n-переходу подходят следующие потоки основных носителей:
. Согласно
(2.1) к p–n-переходу подходят следующие потоки основных носителей:
n![]() =
=![]() n
n![]()
![]()
![]() S,
S,
p![]() =
=![]() p
p![]()
![]()
![]() S.
S.
В соответствии с законом
Больцмана преодолеть потенциальный барьер qV![]() сможет только n
сможет только n![]() exp (-qV
exp (-qV![]() /kT) электронов и p
/kT) электронов и p![]() exp (-qV
exp (-qV![]() /kT) дырок. Поэтому потоки основных
носителей, проходящие через p–n-переход, равны
/kT) дырок. Поэтому потоки основных
носителей, проходящие через p–n-переход, равны
n![]() =
=![]() n
n![]()
![]()
![]() exp (-qV
exp (-qV![]() /kT), (2.4)
/kT), (2.4)
p![]() =
=![]() p
p![]()
![]()
![]() exp (-qV
exp (-qV![]() /kT), (2.5)
/kT), (2.5)
На первых порах после
мысленного приведения n- и p-областей в контакт потоки основных
носителей значительно превосходят потоки неосновных носителей: n![]() >>n
>>n![]() , p
, p![]() >>p
>>p![]() . Но по мере роста объемного заряда увеличивается
потенциальный барьер p–n-перехода qV
. Но по мере роста объемного заряда увеличивается
потенциальный барьер p–n-перехода qV![]() и потоки основных носителей
согласно (2.4) и (2.5) резко уменьшаются. В то же время потоки неосновных
носителей, не зависящие от qV
и потоки основных носителей
согласно (2.4) и (2.5) резко уменьшаются. В то же время потоки неосновных
носителей, не зависящие от qV![]() [ см. (2.2) и
(2.3)] остаются неизменными. Поэтому относительно быстро потенциальный барьер
достигает такой высоты j
[ см. (2.2) и
(2.3)] остаются неизменными. Поэтому относительно быстро потенциальный барьер
достигает такой высоты j![]() = qV
= qV![]() , при которой потоки основных
носителей сравниваются с потоками неосновных носителей:
, при которой потоки основных
носителей сравниваются с потоками неосновных носителей:
n![]() =n
=n![]() , (2.6)
, (2.6)
p![]() =p
=p![]() . (2.7)
. (2.7)
Это соответствует установлению в p–n-переходе состояния динамического равновесия.
Подставляя в (2.6) n![]() из (2.4) и n
из (2.4) и n![]() из (2.2), а в (2.7) p
из (2.2), а в (2.7) p![]() из (2.5) и p
из (2.5) и p![]() из (2.3), получаем
из (2.3), получаем
n![]() exp (-qV
exp (-qV![]() /kT)= n
/kT)= n![]() , (2.8)
, (2.8)
p![]() exp (-qV
exp (-qV![]() /kT)= p
/kT)= p![]() . (2.9)
. (2.9)
Отсюда легко определить
равновесный потенциальный барьер p–n-перехода j![]() = qV
= qV![]() . Из (2.8) находим
. Из (2.8) находим
j![]() = qV
= qV![]() = kTln (n
= kTln (n![]() / n
/ n![]() )= kTln (n
)= kTln (n![]() p
p![]() /n
/n![]() ). (2.10)
). (2.10)
Из (2.9) получаем
j![]() = kTln (p
= kTln (p![]() / p
/ p![]() )=kTln (p
)=kTln (p![]() n
n![]() / n
/ n![]() ). (2.11)
). (2.11)
Из (2.10) и (2.11) следует, что
выравнивание встречных потоков электронов и дырок происходит при одной и той же
высоте потенциального барьера j![]() .
Этот барьер тем выше, чем больше различие в концентрации носителей одного знака
в n- и p-областях полупроводника.
.
Этот барьер тем выше, чем больше различие в концентрации носителей одного знака
в n- и p-областях полупроводника.
Рассчитаем контактную разность потенциалов при 300 К.
n![]() =N
=N![]() =1,0
=1,0![]() 10
10![]()
p![]() =N
=N![]() =1,0
=1,0![]() 10
10![]()
j![]() = kTln(p
= kTln(p![]() n
n![]() /n
/n![]() )=1,38
)=1,38![]() 10
10![]()
![]() 300
300![]() ln
ln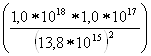 =
=
= 414![]() 10
10![]()
![]() 6,26=2,6
6,26=2,6![]() 10
10![]() (Дж)
(Дж)
V![]() =
=![]() =
=![]() =0,16 (В)
=0,16 (В)
3. Расчет толщины слоя объемного заряда
Для определения вида функции j (x), характеризующей изменение потенциальной энергии электрона при переходе его из n- в p-область (или дырки при переходе ее из p- в n-область), воспользуемся уравнением Пуассона
![]() =
=![]() r (x),
(3.1)
r (x),
(3.1)
в котором r (x) представляет собой объемную плотность зарядов, создающих
поле. Будем полагать, что донорные и акцепторные уровни ионизированы полностью
и слой d![]() покинули практически все
электроны, а слой d
покинули практически все
электроны, а слой d![]() – все дырки. Тогда для
области n (x>0) r
– все дырки. Тогда для
области n (x>0) r![]() (x) » qN
(x) » qN![]() »q n
»q n![]() , для области p (x<0) ) r
, для области p (x<0) ) r![]() (x) » - qN
(x) » - qN![]() » -qp
» -qp![]() . Подставляя это в (3.1), получаем
. Подставляя это в (3.1), получаем
![]() =
=![]() N
N![]() для x>0,
(3.2)
для x>0,
(3.2)
![]() =
=![]() N
N![]() для x<0.
(3.3)
для x<0.
(3.3)
Так как на расстояниях x£d![]() и x ³- d
и x ³- d![]() контактное поле в
полупроводнике отсутствует, то граничными условиями для этих уравнений являются
:
контактное поле в
полупроводнике отсутствует, то граничными условиями для этих уравнений являются
:
j (x) ½![]() =0,
j (x) ½
=0,
j (x) ½![]() =j
=j![]() ; (3.4)
; (3.4)
![]() ½
½![]() =0,
=0, ![]() ½
½![]() =0.
(3.5)
=0.
(3.5)
Решение уравнений (3.2) и (3.3) с граничными условиями (3.4) и (3.5) приводит к следующим результатам:
j=![]() N
N![]() (d
(d![]() - x)
- x)![]() для 0<x< d
для 0<x< d![]() , (3.6)
, (3.6)
j=j![]() -
- ![]() N
N![]() (d
(d![]() + x)
+ x)![]() для - d
для - d![]() <x<0,
(3.7)
<x<0,
(3.7)
d=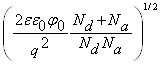 =
=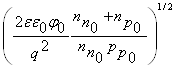 , (3.8)
, (3.8)
d![]() /d
/d![]() =N
=N![]() /N
/N![]() , (3.9)
, (3.9)
Из уравнений (3.6) и
(3.7) видно, что высота потенциального барьера j (x)
является квадратичной функцией координаты x. Толщина слоя объемного заряда согласно (3.8) тем больше,
чем ниже концентрация основных носителей, равная концентрации легирующей
примеси. При этом глубина проникновения контактного поля больше в ту область
полупроводника, которая легирована слабее. При N![]() <<N
<<N![]() , например, практически весь слой локализуется в n-области:
, например, практически весь слой локализуется в n-области:
d » d![]() =
=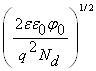 =
=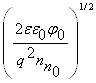 . (3.10)
. (3.10)
Произведенный расчет толщины слоя объемного заряда относится к резкому p–n-переходу, в котором концентрация примесей меняется скачкообразно. Рассчитаем толщину слоя объемного заряда резкого p–n-перехода при 300 К.
d= =
=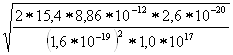 =
=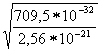 =
=![]() =5,26
=5,26![]() 10
10![]() (см)
(см)
4. Расчет барьерной емкости
Электронно–дырочный переход обладает барьерной, или зарядовой, емкостью, связанной с изменением величины объемного заряда p–n-перехода под влиянием внешнего смещения.
Толщина слоя объемного
заряда d перехода связана с высотой
потенциального барьера j![]() = qV
= qV![]() соотношением (3.8) (или (3.10)
для несимметричного перехода). Поэтому повышение потенциального барьера p–n-перехода при обратном смещении происходит за счет расширения
слоя объемного заряда.
соотношением (3.8) (или (3.10)
для несимметричного перехода). Поэтому повышение потенциального барьера p–n-перехода при обратном смещении происходит за счет расширения
слоя объемного заряда.
При прямом смещении потенциальный барьер p–n-перехода уменьшается за счет суждения слоя объемного заряда.
Для асимметричного p–n-перехода, например, в том и другом случае толщина слоя объемного заряда определяется соотношением, аналогично (3.10):
d = 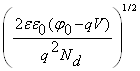 =
=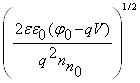 , (4.1)
, (4.1)
Здесь V>0 при прямом и V<0 при обратном смещении.
Установление
стационарного состояния при наличии смещения происходит следующим образом.
Обратное смещение V, приложенное к
полупроводнику, создает в n- и p-областях внешнее поле Е![]() , вызывающее
дрейф основных носителей к омическим контактам, с помощью которых полупроводник
подключается в цепь. Отток основных носителей от p–n-перехода
приводит к обнажению новых слоев ионизированных доноров и акцепторов и
расширению области объемного заряда. Этот процесс продолжается до тех пор, пока
все внешнее смещение V не
окажется приложенным к p–n-переходу.
, вызывающее
дрейф основных носителей к омическим контактам, с помощью которых полупроводник
подключается в цепь. Отток основных носителей от p–n-перехода
приводит к обнажению новых слоев ионизированных доноров и акцепторов и
расширению области объемного заряда. Этот процесс продолжается до тех пор, пока
все внешнее смещение V не
окажется приложенным к p–n-переходу.
Прямое смещение вызывает приток основных носителей к области объемного заряда, в результате которого заряды, созданные внешним источником э.д.с. на омических контактах, переносятся к p–n-переходу и сужают его.
После установления стационарного состояния практически все напряжение V падает на p–n-переходе, так как его сопротивление на много порядков выше сопротивления остальных областей полупроводника.
Таким образом, приложенное к p–n-переходу внешнее напряжение вызывает появление в первый момент времени импульса тока во внешней цепи, приводящего, в конечном счете, к увеличению или уменьшению объемного заряда p–n-перехода. Поэтому переход ведет себя как емкость. Ее называют барьерной, или зарядовой, емкостью, так как она связана с изменением потенциального барьера p–n-перехода. При подаче на переход обратного смещения барьерная емкость заряжается, при подаче прямого смещения – разряжается.
Величину барьерной емкости можно вычислять по формуле плоского конденсатора
С![]() =
=![]() S/d,
(4.2)
S/d,
(4.2)
где S- площадь p–n-перехода; e - диэлектрическая проницаемость
полупроводника; d – толщина слоя
объемного заряда, играющая роль расстояния между обкладками конденсатора.
Отличие от конденсатора состоит в том, что d в выражении (4.3) не является величиной постоянной, а
зависит от внешнего смещения V.
Поэтому и барьерная емкость С![]() также зависит от внешнего смещения
V. Подставляя в (4.2) d из (4.1), получаем
также зависит от внешнего смещения
V. Подставляя в (4.2) d из (4.1), получаем
С![]() =S
=S = S
= S  . (4.3)
. (4.3)
С![]() =S
=S =0,15
=0,15![]()
 =
=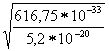 =0,15
=0,15![]()
![]() =0,15
=0,15![]() 3,44
3,44![]() =0,516
=0,516![]() (Ф)
(Ф)
Cписок используемой литературы
1. Епифанов Г.И., Мома Ю.А. Физические основы конструирования и технологии РЭА и ЭВА. - М.: Советское радио, 1979.
2. Пасынков В.В., Сорокин В.С. Материалы электронной техники. – М.: Высшая школа, 1986.
3. Пасынков В.В., Чиркин Л.К. полупроводниковые приборы. – М.: Высшая школа, 1987.
4. Яворский Б.М., Детлаф А.А. Справочник по физике для инженеров и студентов вузов. – М.:Наука,1971.