Контрольная работа: Прогнозирование урожайности различными методами
Содержание
1. Задание
2. Аналитическое выравнивание
3. Метод экспоненциального сглаживания
4. Метод скользящих средних
5. Выравнивание при помощи рядов Фурье
Выводы
1. Задание
По имеющимся исходным данным урожайности озимой пшеницы в Волгоградский области провести расчеты прогнозных значений на последующие шесть лет для выявления закономерных или случайных изменений.
Исходные данные урожайности:
| 1947 | 1948 | 1949 | 1950 | 1951 | 1952 | 1953 | 1954 | 1955 | 1956 | 1957 | 1958 |
| 3,5 | 5,2 | 2,2 | 3,6 | 7,1 | 6,9 | 4,1 | 5,3 | 10,1 | 4,8 | 7,7 | 16,8 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1959 | 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 |
| 9,8 | 14,5 | 13,7 | 19,0 | 5,0 | 12,0 | 11,3 | 17,5 | 13,1 | 17,9 | 9,6 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
2. Аналитическое выравнивание
Выберем в качестве функций регрессии – линейную, параболическую, гиперболическую и показательную:
![]()
![]() .
.
Гиперболическую и показательную можно линеаризовать и применить МНК к этим функциям как к линейным. Для гиперболической функции введем новую переменную:
![]() .
.
Тогда получим:
![]() ,
,
где
![]() .
.
Для показательной функции проведем следующие
преобразования. Прологарифмируем обе части уравнения: ![]() . Сделаем замены:
. Сделаем замены:
![]() ,
, ![]() ,
, ![]() .
.
Получим:
![]() ,
,
откуда найдем: ![]() ,
, ![]() ,
, ![]() .
.
Применим ПО MS Excel 2003 и Stata 7.0. Посчитаем коэффициент корреляции:

Коэффициент корреляции значим.
Построим линейную регрессию
| Регрессионная статистика | ||||||
| Множественный R | 0,717687 | |||||
| R-квадрат | 0,515074 | |||||
| Нормированный R-квадрат | 0,491982 | |||||
| Стандартная ошибка | 3,693991 | |||||
| Наблюдения | 23 | |||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1 | 304,3725 | 304,3725 | 22,30559 | 0,000116 | |
| Остаток | 21 | 286,557 | 13,64557 | |||
| Итого | 22 | 590,9296 | ||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 3,014625 | 1,592152 | 1,893427 | 0,072162 | -0,29644 | 6,325686 |
| Переменная X 1 | 0,548419 | 0,11612 | 4,722879 | 0,000116 | 0,306935 | 0,789903 |
Регрессия для гиперболической функции:
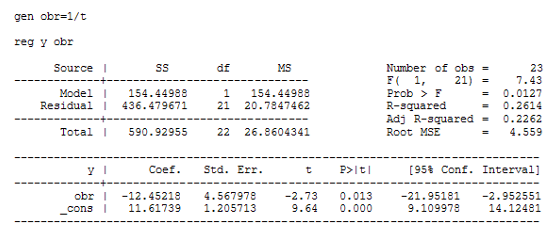
Регрессия для параболической функции:
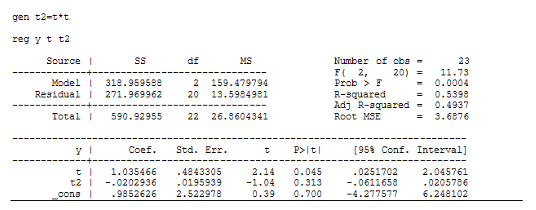
Регрессия для показательной функции:
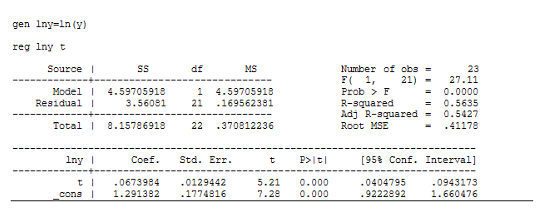
Как видно из этих данных, коэффициент детерминации у
регрессии для гиперболической функции значительно хуже, чем у других моделей. А
константа и коэффициент при переменной ![]() в модели параболической регрессии
не значимы согласно t-критерию Стьюдента.
в модели параболической регрессии
не значимы согласно t-критерию Стьюдента.
Коэффициенты детерминации для моделей линейной и показательной регрессий примерно одиноковы, причем R-квадрат больше у показательной регрессии. Сравним эти 2 модели по другим показателям. Рассчитаем среднюю квадратическую ошибку уравнения тренда и информационные критерии Акейка и Шварца:
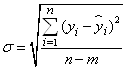 ,
, ![]() ,
, ![]()
Чем меньше значение информационных критериев, тем лучше модель.
Итак, для модели линейной регрессии получим:
AIC=5,131843277
BIC=2,658769213 σ=3,694
Для модели регрессии показательной функции имеем:
AIC= 5,477785725 BIC= 2,831740437 σ=4,028
Все 3 показателя лучше в первом случае.
Применим модель линейной регрессии для аналитического выравнивания исходного ряда. Модель такова:
у=3,01+0,55t;
Значения уровней ряда, полученных по модели, и остатков представлены в следующей таблице:
| Наблюдение | Предсказанное Y | Остатки |
| 1 | 3,563043478 | -0,063043478 |
| 2 | 4,111462451 | 1,088537549 |
| 3 | 4,659881423 | -2,459881423 |
| 4 | 5,208300395 | -1,608300395 |
| 5 | 5,756719368 | 1,343280632 |
| 6 | 6,30513834 | 0,59486166 |
| 7 | 6,853557312 | -2,753557312 |
| 8 | 7,401976285 | -2,101976285 |
| 9 | 7,950395257 | 2,149604743 |
| 10 | 8,498814229 | -3,698814229 |
| 11 | 9,047233202 | -1,347233202 |
| 12 | 9,595652174 | 7,204347826 |
| 13 | 10,14407115 | -0,344071146 |
| 14 | 10,69249012 | 3,807509881 |
| 15 | 11,24090909 | 2,459090909 |
| 16 | 11,78932806 | 7,210671937 |
| 17 | 12,33774704 | -7,337747036 |
| 18 | 12,88616601 | -0,886166008 |
| 19 | 13,43458498 | -2,13458498 |
| 20 | 13,98300395 | 3,516996047 |
| 21 | 14,53142292 | -1,431422925 |
| 22 | 15,0798419 | 2,820158103 |
| 23 | 15,62826087 | -6,02826087 |
Спрогнозируем урожайность озимой пшеницы на последующие 6 лет
| Прогнозные значения | |
| t | y |
| 24 | 16,17667984 |
| 25 | 16,72509881 |
| 26 | 17,27351779 |
| 27 | 17,82193676 |
| 28 | 18,37035573 |
| 29 | 18,9187747 |
Из графика видно, что урожайность с каждым последующим годом будет возрастать и достигнет через шесть лет значения практически в 2 раза большего, чем в 1969 году. Этот результат достигнут в результате существенного роста урожайности зерновых культур.
Проверим наличие автокорреляции в данном динамическом ряду. Для этого составим следующие таблицы:
Расчет коэффициента автокорреляции 1-го порядка
| Год | Фактические уровни y(t) | Уровни, сдвинутые на год y(t-1) | y(t)y(t-1) | y(t)^2 |
| 1 | 3,5 | 9,6 | 33,6 | 12,25 |
| 2 | 5,2 | 3,5 | 18,2 | 27,04 |
| 3 | 2,2 | 5,2 | 11,44 | 4,84 |
| 4 | 3,6 | 2,2 | 7,92 | 12,96 |
| 5 | 7,1 | 3,6 | 25,56 | 50,41 |
| 6 | 6,9 | 7,1 | 48,99 | 47,61 |
| 7 | 4,1 | 6,9 | 28,29 | 16,81 |
| 8 | 5,3 | 4,1 | 21,73 | 28,09 |
| 9 | 10,1 | 5,3 | 53,53 | 102,01 |
| 10 | 4,8 | 10,1 | 48,48 | 23,04 |
| 11 | 7,7 | 4,8 | 36,96 | 59,29 |
| 12 | 16,8 | 7,7 | 129,36 | 282,24 |
| 13 | 9,8 | 16,8 | 164,64 | 96,04 |
| 14 | 14,5 | 9,8 | 142,1 | 210,25 |
| 15 | 13,7 | 14,5 | 198,65 | 187,69 |
| 16 | 19 | 13,7 | 260,3 | 361 |
| 17 | 5 | 19 | 95 | 25 |
| 18 | 12 | 5 | 60 | 144 |
| 19 | 11,3 | 12 | 135,6 | 127,69 |
| 20 | 17,5 | 11,3 | 197,75 | 306,25 |
| 21 | 13,1 | 17,5 | 229,25 | 171,61 |
| 22 | 17,9 | 13,1 | 234,49 | 320,41 |
| 23 | 9,6 | 17,9 | 171,84 | 92,16 |
| Сумма | 220,7 | 220,7 | 2353,68 | 2708,69 |
| Средняя | 9,595652174 | 102,333913 | 117,76913 | |
| Дисперсия | 25,69258979 | Автокорреляция присутствует ( с вероятностью 0,95) | ||
| Коэффициент автокорреляции | 0,399234662 |
Расчет коэффициента автокорреляции 2-го порядка
| Год | Фактические уровни y(t) | Уровни, сдвинутые на 2 года y(t-2) | y(t)y(t-2) | y(t)^2 |
| 1 | 3,5 | 17,9 | 62,65 | 12,25 |
| 2 | 5,2 | 9,6 | 49,92 | 27,04 |
| 3 | 2,2 | 3,5 | 7,7 | 4,84 |
| 4 | 3,6 | 5,2 | 18,72 | 12,96 |
| 5 | 7,1 | 2,2 | 15,62 | 50,41 |
| 6 | 6,9 | 3,6 | 24,84 | 47,61 |
| 7 | 4,1 | 7,1 | 29,11 | 16,81 |
| 8 | 5,3 | 6,9 | 36,57 | 28,09 |
| 9 | 10,1 | 4,1 | 41,41 | 102,01 |
| 10 | 4,8 | 5,3 | 25,44 | 23,04 |
| 11 | 7,7 | 10,1 | 77,77 | 59,29 |
| 12 | 16,8 | 4,8 | 80,64 | 282,24 |
| 13 | 9,8 | 7,7 | 75,46 | 96,04 |
| 14 | 14,5 | 16,8 | 243,6 | 210,25 |
| 15 | 13,7 | 9,8 | 134,26 | 187,69 |
| 16 | 19 | 14,5 | 275,5 | 361 |
| 17 | 5 | 13,7 | 68,5 | 25 |
| 18 | 12 | 19 | 228 | 144 |
| 19 | 11,3 | 5 | 56,5 | 127,69 |
| 20 | 17,5 | 12 | 210 | 306,25 |
| 21 | 13,1 | 11,3 | 148,03 | 171,61 |
| 22 | 17,9 | 17,5 | 313,25 | 320,41 |
| 23 | 9,6 | 13,1 | 125,76 | 92,16 |
| Сумма | 220,7 | 220,7 | 2349,25 | 2708,69 |
| Средняя | 9,595652174 | 102,141304 | 117,76913 | |
| Дисперсия | 25,69258979 | Автокорреляция присутствует ( с вероятностью 0,99) | ||
| Коэффициент автокорреляции | 0,391737999 |
Расчет коэффициента автокорреляции 3-го порядка
| Год | Фактические уровни y(t) | Уровни, сдвинутые на 3 года y(t-3) | y(t)y(t-3) | y(t)^2 |
| 1 | 3,5 | 13,1 | 45,85 | 12,25 |
| 2 | 5,2 | 17,9 | 93,08 | 27,04 |
| 3 | 2,2 | 9,6 | 21,12 | 4,84 |
| 4 | 3,6 | 3,5 | 12,6 | 12,96 |
| 5 | 7,1 | 5,2 | 36,92 | 50,41 |
| 6 | 6,9 | 2,2 | 15,18 | 47,61 |
| 7 | 4,1 | 3,6 | 14,76 | 16,81 |
| 8 | 5,3 | 7,1 | 37,63 | 28,09 |
| 9 | 10,1 | 6,9 | 69,69 | 102,01 |
| 10 | 4,8 | 4,1 | 19,68 | 23,04 |
| 11 | 7,7 | 5,3 | 40,81 | 59,29 |
| 12 | 16,8 | 10,1 | 169,68 | 282,24 |
| 13 | 9,8 | 4,8 | 47,04 | 96,04 |
| 14 | 14,5 | 7,7 | 111,65 | 210,25 |
| 15 | 13,7 | 16,8 | 230,16 | 187,69 |
| 16 | 19 | 9,8 | 186,2 | 361 |
| 17 | 5 | 14,5 | 72,5 | 25 |
| 18 | 12 | 13,7 | 164,4 | 144 |
| 19 | 11,3 | 19 | 214,7 | 127,69 |
| 20 | 17,5 | 5 | 87,5 | 306,25 |
| 21 | 13,1 | 12 | 157,2 | 171,61 |
| 22 | 17,9 | 11,3 | 202,27 | 320,41 |
| 23 | 9,6 | 17,5 | 168 | 92,16 |
| Сумма | 220,7 | 220,7 | 2218,62 | 2708,69 |
| Средняя | 9,595652174 | 96,4617391 | 117,76913 | |
| Дисперсия | 25,69258979 | Автокорреляция отсутствует | ||
| Коэффициент автокорреляции | 0,170679504 |
Как видно из таблиц, обнаружилась автокорреляция только первого и второго порядков. Это говорит о том, что значительное влияние на урожайность озимой пшеницы в данном году оказывает урожайность двух предыдущих лет.
3. Метод экспоненциального сглаживания
Выберем теперь форму зависимости (линейную или параболическую) методом экспоненциального сглаживания.
Рассчитаем начальные условия экспоненциального сглаживания для линейной тенденции:
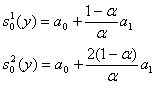 ,
,
где ![]() – параметр сглаживания;
– параметр сглаживания;![]() .
.
Выберем ![]() =0,3
=0,3
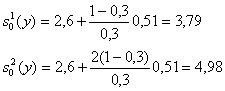
На основе расчета начальных условий определяем оценки коэффициентов и характеристики сглаженных значений.
Формулы расчета оценок коэффициентов:

Формулы расчета характеристик сглаживания динамического ряда:
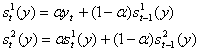
Расчет оценок коэффициентов, характеристик сглаженных
значений, прогнозных значений по линейной форме экспоненциального сглаживания (![]() ) и квадратов
ошибок сведем в таблицу:
) и квадратов
ошибок сведем в таблицу:
| S1 | S2 | a0 | a1 |
|
|
|
| 3,5 | 3,692 | 4,2548 | 3,1292 | -0,3752 | 2,754 | 0,556516 |
| 5,2 | 4,2952 | 4,27096 | 4,31944 | 0,01616 | 4,3356 | 0,74718736 |
| 2,2 | 3,45712 | 3,945424 | 2,968816 | -0,325536 | 2,64328 | 0,196497158 |
| 3,6 | 3,514272 | 3,772963 | 3,255581 | -0,1724608 | 3,08312 | 0,267164934 |
| 7,1 | 4,9485632 | 4,243203 | 5,653923 | 0,47024 | 6,1241632 | 0,95225746 |
| 6,9 | 5,7291379 | 4,837577 | 6,620699 | 0,594373888 | 7,21507264 | 0,099270768 |
| 4,1 | 5,0774828 | 4,933539 | 5,221426 | 0,095962266 | 5,31738842 | 1,482034555 |
| 5,3 | 5,1664897 | 5,026719 | 5,30626 | 0,093180119 | 5,39943995 | 0,009888303 |
| 10,1 | 7,1398938 | 5,871989 | 8,407798 | 0,845269727 | 9,25306811 | 0,717293628 |
| 4,8 | 6,2039363 | 6,004768 | 6,403105 | 0,13277883 | 6,53588335 | 3,013291001 |
| 7,7 | 6,8023618 | 6,323806 | 7,280918 | 0,319037494 | 7,5999555 | 0,010008902 |
| 16,8 | 10,801417 | 8,11485 | 13,48798 | 1,791044614 | 15,2790286 | 2,313354018 |
| 9,8 | 10,40085 | 9,02925 | 11,77245 | 0,914400039 | 12,6868503 | 8,333904844 |
| 14,5 | 12,04051 | 10,23375 | 13,84727 | 1,204503986 | 15,0517701 | 0,304450249 |
| 13,7 | 12,704306 | 11,22197 | 14,18664 | 0,988220769 | 15,174858 | 2,17520614 |
| 19 | 15,222584 | 12,82222 | 17,62295 | 1,600243488 | 19,2231924 | 0,049814834 |
| 5 | 11,13355 | 12,14675 | 10,12035 | -0,67546729 | 9,44488196 | 19,75697565 |
| 12 | 11,48013 | 11,8801 | 11,08016 | -0,26664841 | 10,8135091 | 1,407760654 |
| 11,3 | 11,408078 | 11,69129 | 11,12486 | -0,18880986 | 10,9360534 | 0,132457117 |
| 17,5 | 13,844847 | 12,55271 | 15,13698 | 0,861421592 | 15,9984008 | 2,254800093 |
| 13,1 | 13,546908 | 12,95039 | 14,14342 | 0,397677461 | 14,5411018 | 2,076774272 |
| 17,9 | 15,288145 | 13,88549 | 16,6908 | 0,93510118 | 17,6258978 | 0,075132009 |
| 9,6 | 13,012887 | 13,53645 | 12,48932 | -0,34904247 | 12,1402807 | 6,453026248 |
| 53,38506621 |
Определим начальные условия экспоненциального сглаживания при параболической тенденции:
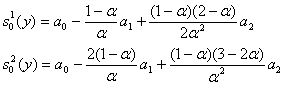
![]()
Выберем ![]()
Соответственно: ![]() = -3,5166014;
= -3,5166014; ![]() =-8,3384654;
=-8,3384654; ![]() =-13,4803294
=-13,4803294
На основе расчета начальных условий определяем оценки коэффициентов и характеристики сглаженных значений. Расчет оценок коэффициентов, характеристик сглаженных значений, прогнозных значений по параболической форме экспоненциального сглаживания и квадратов ошибок сведем в таблицу:
| yi | Характеристики | Оценки коэффициентов | ||||||
| S1 | S2 | S3 | a0 | a1 | a2 | |||
| 3,5 | -2,1132811 | -7,09343 | -12,2029 | 2,737493 | 1,176307311 | -0,00808583 | 3,91383304 | 0,171257789 |
| 5,2 | -0,6506249 | -5,80487 | -10,9233 | 4,539396 | 1,307567679 | 0,002236112 | 5,84696599 | 0,41856499 |
| 2,2 | -0,0804999 | -4,65999 | -9,67067 | 4,067818 | 0,915810984 | -0,02694854 | 4,98399185 | 7,7506106 |
| 3,6 | 0,6556001 | -3,59688 | -8,45591 | 4,301519 | 0,740885761 | -0,03790978 | 5,04312342 | 2,082605212 |
| 7,1 | 1,9444801 | -2,4886 | -7,26245 | 6,036806 | 0,927243389 | -0,02129738 | 6,96427656 | 0,018420853 |
| 6,9 | 2,935584 | -1,40377 | -6,09071 | 6,927341 | 0,900178696 | -0,02172458 | 7,82775603 | 0,860731248 |
| 4,1 | 3,1684672 | -0,48932 | -4,97043 | 6,002929 | 0,477055074 | -0,05145785 | 6,4813078 | 5,670626841 |
| 5,3 | 3,5947738 | 0,327499 | -3,91085 | 5,890979 | 0,300937696 | -0,06069189 | 6,19375797 | 0,798803306 |
| 10,1 | 4,895819 | 1,241163 | -2,88044 | 8,083524 | 0,66559622 | -0,02918445 | 8,74954607 | 1,823725828 |
| 4,8 | 4,8766552 | 1,968261 | -1,9107 | 6,814478 | 0,21148275 | -0,06066067 | 7,02780093 | 4,963096995 |
| 7,7 | 5,4413242 | 2,662874 | -0,99599 | 7,339363 | 0,226893959 | -0,05502572 | 7,56777081 | 0,017484558 |
| 16,8 | 7,7130593 | 3,672911 | -0,06221 | 12,05824 | 1,172083885 | 0,01906433 | 13,2305026 | 12,741312 |
| 9,8 | 8,1304475 | 4,564418 | 0,863117 | 11,5612 | 0,819644091 | -0,00845449 | 12,3808846 | 6,660965133 |
| 14,5 | 9,404358 | 5,532406 | 1,796975 | 13,41283 | 1,040514466 | 0,008532533 | 14,4533811 | 0,00217332 |
| 13,7 | 10,263486 | 6,478622 | 2,733304 | 14,0879 | 0,967225013 | 0,002471645 | 15,0551249 | 1,836363466 |
| 19 | 12,010789 | 7,585056 | 3,703655 | 16,98086 | 1,395610031 | 0,034020784 | 18,3770439 | 0,388074354 |
| 5 | 10,608631 | 8,189771 | 4,600878 | 11,85746 | -0,01686454 | -0,07312702 | 11,8432687 | 46,83032672 |
| 12 | 10,886905 | 8,729198 | 5,426542 | 11,89966 | -0,06882696 | -0,07155927 | 11,8333975 | 0,027756394 |
| 11,3 | 10,969524 | 9,177263 | 6,176686 | 11,55347 | -0,19385244 | -0,07551973 | 11,3624686 | 0,003902328 |
| 17,5 | 12,275619 | 9,796934 | 6,900736 | 14,33679 | 0,397867259 | -0,02609459 | 14,7349986 | 7,645232881 |
| 13,1 | 12,440495 | 10,32565 | 7,585718 | 13,93026 | 0,196638702 | -0,03906748 | 14,1276666 | 1,056098587 |
| 17,9 | 13,532396 | 10,967 | 8,261974 | 15,95817 | 0,567175299 | -0,00872643 | 16,5253867 | 1,88956183 |
| 9,6 | 12,745917 | 11,32278 | 8,874135 | 13,14354 | -0,18901755 | -0,06409432 | 12,956581 | 11,26663598 |
| 114,9243312 |
Определим начальные условия экспоненциального сглаживания при параболической тенденции:
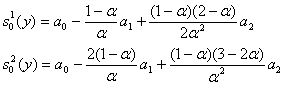
![]()
Выберем ![]()
Соответственно:
![]() = 1,91758335
= 1,91758335
![]() =-1,2595453
=-1,2595453
![]() =-4,60049885
=-4,60049885
На основе расчета начальных условий определяем оценки коэффициентов и характеристики сглаженных значений.
Расчет оценок коэффициентов, характеристик сглаженных
значений, прогнозных значений по параболической форме экспоненциального
сглаживания (![]() ) и квадратов ошибок сведем в
таблицу:
) и квадратов ошибок сведем в
таблицу:
| yi | Характеристики | Оценки коэффициентов |
|
|||||
| S1 | S2 | S3 | a0 | a1 | a2 | |||
| 3,5 | 4,0123083 | 0,322011 | -3,12375 | 7,947147 | 1,813620275 | 0,04491565 | 9,76177562 | 0,742657215 |
| 5,2 | 5,7486158 | 1,949992 | -1,60162 | 9,794246 | 1,862385849 | 0,045368582 | 11,6576611 | 3,450904714 |
| 2,2 | 5,9440311 | 3,148204 | -0,17668 | 8,210805 | 0,696151358 | -0,09717296 | 8,91167811 | 6,308526949 |
| 3,6 | 5,9308218 | 3,982989 | 1,071224 | 6,914721 | -0,07996759 | -0,17704896 | 6,8504266 | 0,903310726 |
| 7,1 | 7,9915752 | 5,185565 | 2,305526 | 10,72356 | 1,132323907 | -0,01359714 | 11,8559729 | 0,891187203 |
| 6,9 | 8,6841027 | 6,235126 | 3,484406 | 10,83134 | 0,76321248 | -0,05542235 | 11,5960834 | 1,679832129 |
| 4,1 | 8,6888719 | 6,97125 | 4,530459 | 9,683325 | 0,049851182 | -0,13282693 | 9,74199756 | 1,085758914 |
| 5,3 | 9,0822103 | 7,604538 | 5,452683 | 9,8857 | -0,00649776 | -0,12382952 | 9,88686868 | 0,012798695 |
| 10,1 | 10,857547 | 8,580441 | 6,39101 | 13,22233 | 1,059105338 | 0,01610373 | 14,2815645 | 0,516149625 |
| 4,8 | 9,910283 | 8,979393 | 7,167525 | 9,960194 | -0,43707812 | -0,16181241 | 9,53620743 | 3,371657732 |
| 7,7 | 12,007198 | 9,887735 | 7,983588 | 14,34198 | 1,112672366 | 0,039547931 | 15,4554323 | 2,086775904 |
| 16,8 | 13,055039 | 10,83793 | 8,83989 | 15,49123 | 1,158089937 | 0,040238477 | 16,650127 | 1,322792148 |
| 9,8 | 14,238527 | 11,85811 | 9,745355 | 16,88662 | 1,274192695 | 0,049163686 | 18,162018 | 1,35028586 |
| 14,5 | 15,666969 | 13,00077 | 10,72198 | 18,72059 | 1,510309073 | 0,07115812 | 20,23343 | 1,521349651 |
| 13,7 | 17,026878 | 14,2086 | 11,76796 | 20,2228 | 1,56621064 | 0,069363232 | 21,791418 | 2,532611258 |
| 19 | 17,978815 | 15,33966 | 12,83947 | 20,75693 | 1,262936101 | 0,025523494 | 22,0201889 | 3,313087501 |
| 5 | 15,34517 | 15,34132 | 13,59003 | 13,60159 | -1,65662782 | -0,32095738 | 11,9964693 | 7,820240766 |
| 12 | 16,531619 | 15,69841 | 14,22254 | 16,72218 | -0,25277423 | -0,11803844 | 16,4763703 | 7,972884921 |
| 11,3 | 16,612133 | 15,97252 | 14,74754 | 16,66636 | -0,28139592 | -0,10751882 | 16,3907461 | 0,167488742 |
| 17,5 | 18,018493 | 16,58632 | 15,29917 | 19,5957 | 0,751423356 | 0,0266386 | 20,347482 | 0,907290518 |
| 13,1 | 16,092945 | 16,4383 | 15,64091 | 14,60483 | -1,23246052 | -0,20989346 | 13,3944003 | 3,219872312 |
| 17,9 | 16,845062 | 16,56033 | 15,91674 | 16,77093 | -0,21852822 | -0,06591395 | 16,5545712 | 4,183779005 |
| 9,6 | 16,321543 | 16,4887 | 16,08832 | 15,58687 | -0,61020409 | -0,10423889 | 14,9820974 | 0,013901034 |
| 55,37514352 |
Определим начальные условия экспоненциального сглаживания при параболической тенденции:
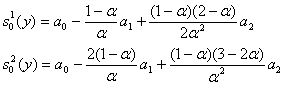
![]()
Выберем ![]()
Соответственно:
![]() = 3,0313761
= 3,0313761
![]() =1,06416203
=1,06416203
![]() =-0,970755225
=-0,970755225
На основе расчета начальных условий определяем оценки коэффициентов и характеристики сглаженных значений.
Расчет оценок коэффициентов, характеристик сглаженных
значений, прогнозных значений по параболической форме экспоненциального
сглаживания (![]() ) и квадратов ошибок сведем в
таблицу:
) и квадратов ошибок сведем в
таблицу:
| yi | Характеристики | Оценки коэффициентов | ||||||
| S1 | S2 | S3 | a0 | a1 | a2 | |||
| 3,5 | 5,3788257 | 2,790027 | 0,533558 | 8,299952 | 2,24282099 | 0,147701582 | 10,5536813 | 2,734661735 |
| 5,2 | 7,1472954 | 4,532935 | 2,133309 | 9,976391 | 2,076938886 | 0,095437634 | 12,0578839 | 5,098039615 |
| 2,2 | 6,8483772 | 5,459112 | 3,46363 | 7,631426 | -0,01682611 | -0,26942947 | 7,65089649 | 1,564742023 |
| 3,6 | 6,4690263 | 5,863078 | 4,423409 | 6,241255 | -0,89293167 | -0,37054215 | 5,41697437 | 0,233313758 |
| 7,1 | 9,0014158 | 7,118413 | 5,50141 | 11,15042 | 1,669114 | 0,118222485 | 12,8265216 | 0,000703397 |
| 6,9 | 9,5208495 | 8,079388 | 6,532601 | 10,85699 | 0,797136961 | -0,04681077 | 11,6552198 | 1,836620752 |
| 4,1 | 9,1925097 | 8,524636 | 7,329415 | 9,333035 | -0,37506983 | -0,23437677 | 8,98543167 | 0,081471237 |
| 5,3 | 9,5155058 | 8,920984 | 7,966043 | 9,749608 | -0,16430499 | -0,1601865 | 9,59813271 | 0,161497319 |
| 10,1 | 11,709303 | 10,03631 | 8,79415 | 13,81313 | 1,78550802 | 0,191480082 | 15,6169656 | 0,380646557 |
| 4,8 | 10,105582 | 10,06402 | 9,302098 | 9,426785 | -1,09285126 | -0,32015981 | 8,38518453 | 0,469477846 |
| 7,7 | 12,823349 | 11,16775 | 10,04836 | 15,01515 | 1,937829195 | 0,238313566 | 16,9813782 | 0,006622415 |
| 16,8 | 13,89401 | 12,25825 | 10,93232 | 15,83958 | 1,572441642 | 0,137696713 | 17,4215037 | 3,692176522 |
| 9,8 | 15,136406 | 13,40952 | 11,9232 | 17,10387 | 1,525483554 | 0,106920913 | 18,6350679 | 2,673447105 |
| 14,5 | 16,681843 | 14,71845 | 13,0413 | 18,93149 | 1,75420453 | 0,127220923 | 20,6937846 | 2,86890619 |
| 13,7 | 18,089106 | 16,06671 | 14,25146 | 20,31865 | 1,67049331 | 0,092065566 | 21,9933807 | 3,216214243 |
| 19 | 18,933464 | 17,21341 | 15,43624 | 20,5964 | 1,057851513 | -0,02538566 | 21,6545716 | 2,115778599 |
| 5 | 15,040078 | 16,34408 | 15,79938 | 11,88738 | -3,74509187 | -0,82164528 | 8,47983483 | 0,518637869 |
| 12 | 16,744047 | 16,50407 | 16,08125 | 16,8012 | -0,12441845 | -0,08125883 | 16,6800788 | 6,863987211 |
| 11,3 | 16,766428 | 16,60901 | 16,29236 | 16,76461 | -0,14275806 | -0,07077229 | 16,6243542 | 0,030851434 |
| 17,5 | 18,579857 | 17,39735 | 16,73435 | 20,28188 | 1,596467573 | 0,230894027 | 21,9049998 | 0,366024715 |
| 13,1 | 15,787914 | 16,75358 | 16,74204 | 13,84506 | -2,16385405 | -0,43430858 | 11,7755167 | 0,030806121 |
| 17,9 | 16,912748 | 16,81724 | 16,77212 | 17,05863 | 0,142041992 | 0,022392189 | 17,2009276 | 1,957403589 |
| 9,6 | 16,187649 | 16,56541 | 16,68944 | 15,55616 | -0,64652505 | -0,11276768 | 14,9159978 | 0,033856812 |
| 36,93588706 |
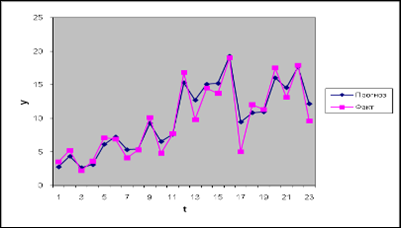
Постоим соответственно графики значений ![]() по исходным данным линейной
и параболической формы сглаживания.
по исходным данным линейной
и параболической формы сглаживания.
Линейная форма:
Параболическая форма:
1) ![]() =0,2
=0,2
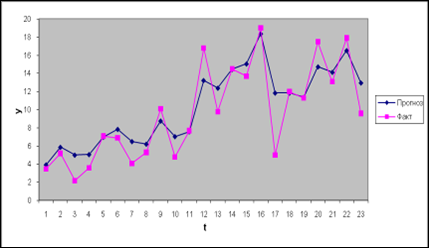
2) ![]() =0,3
=0,3
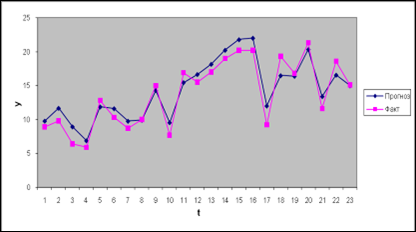
3) ![]() =0,4
=0,4
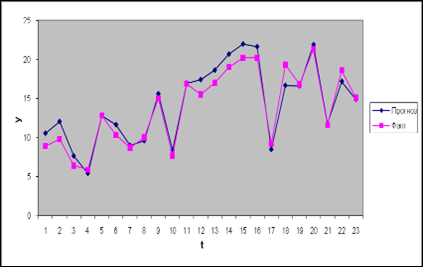
Видно,что параболическая форма зафисимости экспоненциального сглаживания лучше подогнана к исходным данным.Следовательно, параболическая форма более подходит для прогноза. Сделаем прогноз на 6 лет и представим графической формой.
| t | 24 | 25 | 26 | 27 | 28 | 29 |
|
|
14,916 | 14,28855 | 13,67381 | 13,0718 | 12,4825 | 11,90591 |
4. Метод скользящих средних
Выберем в качестве параметров скольжения 3, 5, 9. Причем при параметре, равном 5, используем весовые коэффициенты для расчета скользящей средней. Для определения этих весовых коэффициентов применим треугольник Паскаля. Таким образом, весовыми коэффициенты будут следующие числа: 1, 2, 4, 2, 1.
Для начала проведем расчеты при параметре скольжения 3. Данные приведем в следующей таблице:
| t | y | Скользящая сумма | Скользящая средняя | Прирост | Ускорения |
| 1 | 3,5 | ||||
| 2 | 5,2 | 25,1 | 8,367 | ||
| 3 | 2,2 | 22,1 | 7,367 | -1 | |
| 4 | 3,6 | 25,1 | 8,367 | 1 | 2 |
| 5 | 7,1 | 29 | 9,667 | 1,3 | 0,3 |
| 6 | 6,9 | 31,8 | 10,6 | 0,933 | -0,367 |
| 7 | 4,1 | 29 | 9,667 | -0,933 | -1,867 |
| 8 | 5,3 | 33,7 | 11,233 | 1,567 | 2,500 |
| 9 | 10,1 | 32,7 | 10,9 | -0,333 | -1,900 |
| 10 | 4,8 | 39,6 | 13,2 | 2,300 | 2,633 |
| 11 | 7,7 | 40,1 | 13,367 | 0,167 | -2,133 |
| 12 | 16,8 | 49,4 | 16,467 | 3,100 | 2,933 |
| 13 | 9,8 | 51,5 | 17,167 | 0,700 | -2,400 |
| 14 | 14,5 | 56,2 | 18,733 | 1,567 | 0,867 |
| 15 | 13,7 | 59,4 | 19,8 | 1,067 | -0,500 |
| 16 | 19 | 49,6 | 16,533 | -3,267 | -4,333 |
| 17 | 5 | 48,7 | 16,233 | -0,300 | 2,967 |
| 18 | 12 | 45,3 | 15,1 | -1,133 | -0,833 |
| 19 | 11,3 | 57,4 | 19,133 | 4,033 | 5,167 |
| 20 | 17,5 | 49,7 | 16,567 | -2,567 | -6,600 |
| 21 | 13,1 | 51,5 | 17,167 | 0,600 | 3,167 |
| 22 | 17,9 | 45,3 | 15,1 | -2,067 | -2,667 |
| 23 | 9,6 |
Построим модель регрессии на ряд скользящих средних. Сравним модели линейной регрессии и параболической:
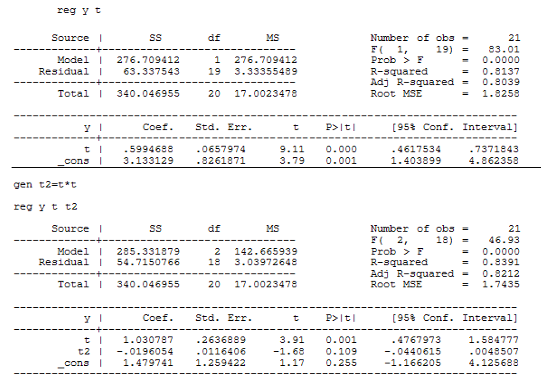
Выберем модель параболической регрессии на основании лучших коэффициента детерминации и скорректированного коэффициента детерминации у этой модели. Получим следующую модель:
y=1.4+1.03t-0.02 ![]()
Спрогнозируем значения скользящих средних на последующие 6 лет:
| t |
|
| 23 | 16,4389 |
| 24 | 16,0816 |
| 25 | 15,6469 |
| 26 | 15,1348 |
| 27 | 14,5454 |
| 28 | 13,8786 |
Рассчитаем значения исходного ряда на будущий период, используя формулу:
![]()
и приведем в следующей таблице:
| Значения скользящих средних, полученные по модели | t | Значения у |
| 1 | 3,5 | |
| 8,51976912 | 2 | 5,2 |
| 9,052236652 | 3 | 2,2 |
| 9,584704185 | 4 | 3,6 |
| 10,11717172 | 5 | 7,1 |
| 10,64963925 | 6 | 6,9 |
| 11,18210678 | 7 | 4,1 |
| 11,71457431 | 8 | 5,3 |
| 12,24704185 | 9 | 10,1 |
| 12,77950938 | 10 | 4,8 |
| 13,31197691 | 11 | 7,7 |
| 13,84444444 | 12 | 16,8 |
| 14,37691198 | 13 | 9,8 |
| 14,90937951 | 14 | 14,5 |
| 15,44184704 | 15 | 13,7 |
| 15,97431457 | 16 | 19 |
| 16,50678211 | 17 | 5 |
| 17,03924964 | 18 | 12 |
| 17,57171717 | 19 | 11,3 |
| 18,1041847 | 20 | 17,5 |
| 18,63665224 | 21 | 13,1 |
| 19,16911977 | 22 | 17,9 |
| 16,3222 | 23 | 9,6 |
| Прогноз на будущее | ||
| 16,9218 | 24 | 21,47 |
| 17,5214 | 25 | 19,70 |
| 18,1209 | 26 | 11,40 |
| 18,7205 | 27 | 23,27 |
| 19,3201 | 28 | 21,50 |
| 29 | 13,20 |
Значения урожайности по годам вместе с прогнозными значениями представим на графике:
Проведем расчеты для параметра 5 с применением треугольника Паскаля.
| t | y | Скользящая сумма | Скользящая средняя | Прирост | Ускорения |
| 1 | 3,5 | ||||
| 2 | 5,2 | ||||
| 3 | 2,2 | 37 | 3,700 | ||
| 4 | 3,6 | 45,1 | 4,510 | 0,81 | |
| 5 | 7,1 | 55,7 | 5,570 | 1,06 | 0,25 |
| 6 | 6,9 | 58,9 | 5,890 | 0,320 | -0,740 |
| 7 | 4,1 | 58 | 5,800 | -0,090 | -0,410 |
| 8 | 5,3 | 61,3 | 6,130 | 0,330 | 0,420 |
| 9 | 10,1 | 72,4 | 7,240 | 1,110 | 0,780 |
| 10 | 4,8 | 76,9 | 7,690 | 0,450 | -0,660 |
| 11 | 7,7 | 93,9 | 9,390 | 1,700 | 1,250 |
| 12 | 16,8 | 121,5 | 12,150 | 2,760 | 1,060 |
| 13 | 9,8 | 123,2 | 12,320 | 0,170 | -2,590 |
| 14 | 14,5 | 140,8 | 14,080 | 1,760 | 1,590 |
| 15 | 13,7 | 136,6 | 13,660 | -0,420 | -2,180 |
| 16 | 19 | 139,9 | 13,990 | 0,330 | 0,750 |
| 17 | 5 | 107 | 10,700 | -3,290 | -3,620 |
| 18 | 12 | 117,1 | 11,710 | 1,010 | 4,300 |
| 19 | 11,3 | 122,3 | 12,230 | 0,520 | -0,490 |
| 20 | 17,5 | 148,7 | 14,870 | 2,640 | 2,120 |
| 21 | 13,1 | 144,1 | 14,410 | -0,460 | -3,100 |
| 22 | 17,9 | ||||
| 23 | 9,6 |
Построим модель регрессии на ряд скользящих средних. Сравним модели линейной регрессии и параболической:
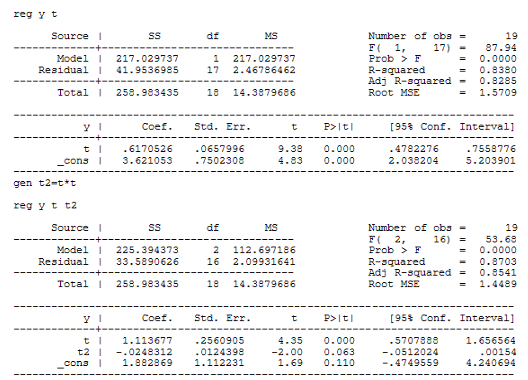
Выберем модель параболической регрессии на основании лучших R-квадрата и скорректированного R-квадрата у этой модели. Получим следующую модель:
y=1.88+1.11t-0.02![]()
Отобразим ее на графике:
Спрогнозируем значения скользящих средних на последующие 6 лет:
| t |
|
| 23 | 17,1962 |
| 24 | 17,8133 |
| 25 | 18,4303 |
| 26 | 19,0474 |
| 27 | 19,6644 |
| 28 | 20,2815 |
Рассчитаем значения исходного ряда на будущий период, используя формулу:
![]()
и приведем в следующей таблице:
| Значения скользящих средних, полученные по модели | t | Значения у |
| 1 | 3,5 | |
| 2 | 5,2 | |
| 8,8125 | 3 | 2,2 |
| 9,3924 | 4 | 3,6 |
| 9,9723 | 5 | 7,1 |
| 10,5522 | 6 | 6,9 |
| 11,1321 | 7 | 4,1 |
| 11,7120 | 8 | 5,3 |
| 12,2919 | 9 | 10,1 |
| 12,8718 | 10 | 4,8 |
| 13,4517 | 11 | 7,7 |
| 14,0316 | 12 | 16,8 |
| 14,6115 | 13 | 9,8 |
| 15,1914 | 14 | 14,5 |
| 15,7713 | 15 | 13,7 |
| 16,3512 | 16 | 19 |
| 16,9311 | 17 | 5 |
| 17,5109 | 18 | 12 |
| 18,0908 | 19 | 11,3 |
| 18,6707 | 20 | 17,5 |
| 19,2506 | 21 | 13,1 |
| 15,9621 | 22 | 17,9 |
| 16,5792 | 23 | 9,6 |
| Прогноз на будущее | ||
| 17,1962 | 24 | 25,12 |
| 17,8133 | 25 | 28,25 |
| 18,4303 | 26 | -22,12 |
| 19,0474 | 27 | 49,53 |
| 28 | 92,10 | |
| 29 | -175,87 |
Из таблицы видно, что при t=29 значение урожайности отрицательное, чего не может быть в принципе. Этот факт объясняется тем, что исходный ряд плохо аппроксимируется нормальным распределением.
Проведем расчеты при параметре скольжения 9. Данные приведем в следующей таблице:
| t | y | Скользящая сумма | Скользящая средняя | Прирост | Ускорения |
| 1 | 3,5 | ||||
| 2 | 5,2 | ||||
| 3 | 2,2 | ||||
| 4 | 3,6 | ||||
| 5 | 7,1 | 48 | 5,333 | ||
| 6 | 6,9 | 49,3 | 5,478 | 0,144 | |
| 7 | 4,1 | 51,8 | 5,756 | 0,278 | 0,133 |
| 8 | 5,3 | 66,4 | 7,378 | 1,622 | 1,344 |
| 9 | 10,1 | 72,6 | 8,067 | 0,689 | -0,933 |
| 10 | 4,8 | 80 | 8,889 | 0,822 | 0,133 |
| 11 | 7,7 | 86,8 | 9,644 | 0,756 | -0,067 |
| 12 | 16,8 | 101,7 | 11,300 | 1,656 | 0,900 |
| 13 | 9,8 | 101,4 | 11,267 | -0,033 | -1,689 |
| 14 | 14,5 | 103,3 | 11,478 | 0,211 | 0,244 |
| 15 | 13,7 | 109,8 | 12,200 | 0,722 | 0,511 |
| 16 | 19 | 119,6 | 13,289 | 1,089 | 0,367 |
| 17 | 5 | 115,9 | 12,878 | -0,411 | -1,500 |
| 18 | 12 | 124 | 13,778 | 0,900 | 1,311 |
| 19 | 11,3 | 119,1 | 13,233 | -0,544 | -1,444 |
| 20 | 17,5 | ||||
| 21 | 13,1 | ||||
| 22 | 17,9 | ||||
| 23 | 9,6 |
Построим модель регрессии на ряд скользящих средних. Сравним модели линейной регрессии и параболической:
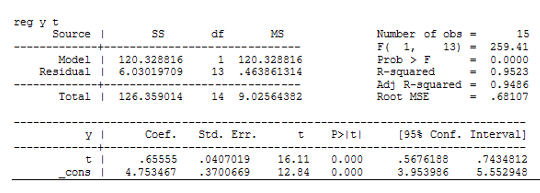
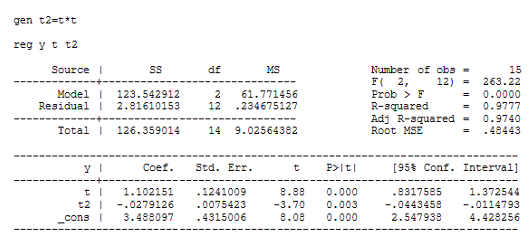
Выберем модель параболической регрессии на основании лучших R-квадрата и скорректированного R-квадрата у этой модели. Получим следующую модель:
y=3.49+1.1t-3.49![]()
Спрогнозируем значения скользящих средних на последующие 6 лет:
| t |
|
| 23 | 17,8644 |
| 24 | 18,5200 |
| 25 | 19,1756 |
| 26 | 19,8311 |
| 27 | 20,4867 |
| 28 | 21,1422 |
Рассчитаем значения исходного ряда на будущий период, используя формулу:
![]()
и приведем в следующей таблице:
| Значения скользящих средних, полученные по модели | t | Значения у |
| 1 | 3,5 | |
| 2 | 5,2 | |
| 3 | 2,2 | |
| 4 | 3,6 | |
| 9,9721 | 5 | 7,1 |
| 10,5981 | 6 | 6,9 |
| 11,2241 | 7 | 4,1 |
| 11,8501 | 8 | 5,3 |
| 12,4761 | 9 | 10,1 |
| 13,1021 | 10 | 4,8 |
| 13,7281 | 11 | 7,7 |
| 14,3541 | 12 | 16,8 |
| 14,9801 | 13 | 9,8 |
| 15,6061 | 14 | 14,5 |
| 16,2321 | 15 | 13,7 |
| 16,8580 | 16 | 19 |
| 17,4840 | 17 | 5 |
| 18,1100 | 18 | 12 |
| 18,7360 | 19 | 11,3 |
| 15,2422 | 20 | 17,5 |
| 15,8978 | 21 | 13,1 |
| 16,5533 | 22 | 17,9 |
| 17,2089 | 23 | 9,6 |
| Прогноз на будущее | ||
| 16,6847 | 24 | 51,99 |
| 16,2773 | 25 | 18,31 |
| 26 | 3,56 | |
| 27 | 9,82 | |
| 28 | 8,38 | |
| 29 | 13,83 |
5. Выравнивание при помощи рядов Фурье
Пусть ряд содержит циклическую составляющую, выраженную некоторой функцией от времени y(t) c известными периодами, нацело делящими n. То есть периоды y(t) задаются числами n/kj, j=1, …, m, где (k1, …,km) – подмножество последовательности целых чисел 1, …, (n-1)/2, если n нечетное. Представим y(t) в виде ряда Фурье – линейной комбинации синусов и косинусов для n нечетного:
![]()
Рассмотрим теперь задачу гармонического анализа ряда, состоящую в оценивании параметров a0, ak, bk:
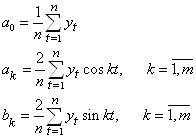
Последовательные значения t определяются 0 с увеличением,
равным ![]() .
.
Расчет показателей, необходимых для выравнивания с помощью ряда Фурье, представлен в следующей таблице:
| Год | t | y | y cos t | y sin t |
|
y cos 2t | y sin 2t |
|
||
| 1 | 0 | 3,5 | 3,5 | 0 | 7,765 | 18,192 | 3,5 | 0 | 8,132 | 21,456 |
| 2 | 0,273 | 5,2 | 5,007 | 1,403 | 6,611 | 1,992 | 4,443 | 2,702 | 6,252 | 1,107 |
| 3 | 0,546 | 2,2 | 1,880 | 1,143 | 5,679 | 12,103 | 1,012 | 1,953 | 4,698 | 6,242 |
| 4 | 0,820 | 3,6 | 2,457 | 2,631 | 5,037 | 2,065 | -0,246 | 3,592 | 3,721 | 0,015 |
| 5 | 1,093 | 7,1 | 3,266 | 6,304 | 4,733 | 5,602 | -4,094 | 5,800 | 3,464 | 13,220 |
| 6 | 1,366 | 6,9 | 1,403846 | 6,756 | 4,790 | 4,452 | -6,329 | 2,749 | 3,938 | 8,775 |
| 7 | 1,639 | 4,1 | -0,280 | 4,090 | 5,203 | 1,217 | -4,062 | -0,558 | 5,016 | 0,839 |
| 8 | 1,912 | 5,3 | -1,775 | 4,994 | 5,942 | 0,412 | -4,111 | -3,345 | 6,474 | 1,379 |
| 9 | 2,185 | 10,1 | -5,824 | 8,251 | 6,952 | 9,910 | -3,382 | -9,517 | 8,049 | 4,207 |
| 10 | 2,459 | 4,8 | -3,723 | 3,029 | 8,158 | 11,276 | 0,977 | -4,700 | 9,500 | 22,090 |
| 11 | 2,732 | 7,7 | -7,06253 | 3,068 | 9,471 | 3,135 | 5,256 | -5,627 | 10,667 | 8,803 |
| 12 | 3,005 | 16,8 | -16,644 | 2,288 | 10,792 | 36,090 | 16,177 | -4,533 | 11,495 | 28,143 |
| 13 | 3,278 | 9,8 | -9,709 | -1,334 | 12,026 | 4,953 | 9,437 | 2,644 | 12,030 | 4,971 |
| 14 | 3,551 | 14,5 | -13,300 | -5,777 | 13,0785 | 2,021 | 9,897 | 10,597 | 12,383 | 4,482 |
| 15 | 3,825 | 13,7 | -10,627 | -8,646 | 13,873 | 0,030 | 2,787 | 13,413 | 12,680 | 1,040 |
| 16 | 4,098 | 19 | -10,9569 | -15,522 | 14,350 | 21,618 | -6,363 | 17,903 | 13,008 | 35,905 |
| 17 | 4,371 | 5 | -1,674 | -4,711 | 14,475 | 89,779 | -3,879 | 3,155 | 13,374 | 70,119 |
| 18 | 4,644 | 12 | -0,819 | -11,972 | 14,238 | 5,009 | -11,888 | 1,634 | 13,698 | 2,884 |
| 19 | 4,917 | 11,3 | 2,299 | -11,064 | 13,657 | 5,553 | -10,364 | -4,502 | 13,836 | 6,430 |
| 20 | 5,190 | 17,5 | 8,051 | -15,538 | 12,774 | 22,336 | -10,092 | -14,297 | 13,620 | 15,056 |
| 21 | 5,464 | 13,1 | 8,941446 | -9,574 | 11,656 | 2,087 | -0,894 | -13,069 | 12,922 | 0,032 |
| 22 | 5,737 | 17,9 | 15,294 | -9,301 | 10,3844 | 56,485 | 8,235 | -15,893 | 11,702 | 38,410 |
| 23 | 6,010 | 9,6 | 9,244 | -2,590 | 9,055 | 0,297 | 8,202 | -4,988 | 10,041 | 0,194 |
| n=23 | ∑ | 220,7 | -21,050 | -52,072 | 220,7 | 316,615 | 4,219 | -14,886 | 220,700 | 295,799 |
| Год | t | y | y cos 3t | y sin 3t |
|
(yi-yi2) |
| 1 | 0 | 3,5 | 3,5 | 0 | 6,496 | 8,976 |
| 2 | 0,273 | 5,2 | 3,549 | 3,800 | 3,47017 | 2,992 |
| 3 | 0,546 | 2,2 | -0,150 | 2,195 | 2,5366 | 0,113 |
| 4 | 0,820 | 3,6 | -2,793 | 2,272 | 3,55156 | 0,002 |
| 5 | 1,093 | 7,1 | -7,034 | -0,967 | 5,39523 | 2,906 |
| 6 | 1,366 | 6,9 | -3,979 | -5,637 | 6,74298 | 0,025 |
| 7 | 1,639 | 4,1 | 0,834 | -4,014 | 6,91425 | 7,920 |
| 8 | 1,912 | 5,3 | 4,528 | -2,754 | 6,26056 | 0,923 |
| 9 | 2,185 | 10,1 | 9,725 | 2,725 | 5,85861 | 17,989 |
| 10 | 2,459 | 4,8 | 2,208 | 4,262 | 6,72393 | 3,702 |
| 11 | 2,732 | 7,7 | -2,579 | 7,255 | 9,06763 | 1,870 |
| 12 | 3,005 | 16,8 | -15,409 | 6,693 | 12,0877 | 22,206 |
| 13 | 3,278 | 9,8 | -8,989 | -3,904 | 14,4381 | 21,512 |
| 14 | 3,551 | 14,5 | -4,856 | -13,663 | 15,0781 | 0,334 |
| 15 | 3,825 | 13,7 | 6,303 | -12,164 | 13,9511 | 0,063 |
| 16 | 4,098 | 19 | 18,295 | -5,126 | 12,0474 | 48,339 |
| 17 | 4,371 | 5 | 4,272 | 2,598 | 10,7918 | 33,545 |
| 18 | 4,644 | 12 | 2,441 | 11,749 | 11,1343 | 0,749 |
| 19 | 4,917 | 11,3 | -6,516 | 9,232 | 12,9175 | 2,616 |
| 20 | 5,190 | 17,5 | -17,337 | 2,383 | 14,9303 | 6,603 |
| 21 | 5,464 | 13,1 | -10,162 | -8,267 | 15,6291 | 6,396 |
| 22 | 5,737 | 17,9 | -1,222 | -17,858 | 14,0876 | 14,534 |
| 23 | 6,010 | 9,6 | 6,553 | -7,016 | 10,5895 | 0,979 |
| n=23 | ∑ | 220,7 | -18,815 | -26,207 | 220,7 | 205,297 |
Рассчитаем параметры:
| a0 | a1 | b1 | a2 | b2 | a3 | b3 |
| 9,596 | -1,830 | -4,528 | 0,367 | -1,294 | -1,636 | -2,279 |
Таким образом, получили модели:
- для гармоники первого порядка ![]() = 9,569-1,83 cos t-4.528 sin t
= 9,569-1,83 cos t-4.528 sin t
- для гармоники второго порядка ![]() = 9,569-1,83 cos t-4.528 sin t +
= 9,569-1,83 cos t-4.528 sin t +
+ 0,367 соs 2t-1.294 sin 2t
- для гармоники третьего порядка ![]() =9,569-1,83 cos t-4.528 sin t +
=9,569-1,83 cos t-4.528 sin t +
+ 0,367 соs 2t-1.294 sin 2t-1.636 cos3t-2.279 sin 3t
Исследуем модель с гармоникой первого порядка
Прогнозные значения
| Год | t |
|
| 24 | 6,283 | 7,765199 |
| 25 | 6,556 | 6,611 |
| 26 | 6,830 | 5,679 |
| 27 | 7,103 | 5,037 |
| 28 | 7,376 | 4,733 |
| 29 | 7,649 | 4,790 |
Изучим модель с гармоникой второго порядка
Прогнозные значения
| Год | t |
|
| 24 | 6,283 | 8,132054 |
| 25 | 6,556 | 6,252 |
| 26 | 6,830 | 4,698 |
| 27 | 7,103 | 3,721 |
| 28 | 7,376 | 3,464 |
| 29 | 7,649 | 3,938 |
Исследуем модель с гармоникой третьего порядка
Прогнозные значения
| Год | t |
|
| 24 | 6,283 | 6,496 |
| 25 | 6,556 | 3,470 |
| 26 | 6,830 | 2,537 |
| 27 | 7,103 | 3,552 |
| 28 | 7,376 | 5,395 |
| 29 | 7,649 | 6,743 |
Выводы
Были рассмотрены четыре метода прогнозирования – аналитическое выравнивание методом наименьших квадратов, метод экспоненциального сглаживания, метод скользящих средних, и выравнивание при помощи рядов Фурье. Выберем наиболее подходящий метод, который дает наиболее правдоподобный прогноз.
Выравнивание с помощью рядов Фурье дает сумму квадратов
ошибок от 200 до 300 (в зависимости от гармоники). Метод экспоненциального
сглаживания дает результат получше: для параболического тренда сумма квадратов
ошибок колеблется от 36 до 115 (при ![]() сумма квадратов ошибок равна 115;
при
сумма квадратов ошибок равна 115;
при ![]() =0,4
сумма квадратов ошибок 36);Для линейной тенденции сумма квадратов ошибок равна
55. Аналитическое выравнивание МНК дает сумму квадратов ошибок, равную 272.
Лучше всего описывает тренд метод скользящих средних с параметром n=3. Он дает
сумму квадратов ошибок, равную 63.
=0,4
сумма квадратов ошибок 36);Для линейной тенденции сумма квадратов ошибок равна
55. Аналитическое выравнивание МНК дает сумму квадратов ошибок, равную 272.
Лучше всего описывает тренд метод скользящих средних с параметром n=3. Он дает
сумму квадратов ошибок, равную 63.