Контрольная работа: Статистическая обработка результатов прямых многоразовых измерений с независимыми равноточными наблюдениями
Розрахунково-графічне завдання
з теми:
«Статистична обробка результатів прямих багаторазових вимірювань з незалежними рівноточними спостереженнями»
Виконала:
Студентка групиАП-48б
Арсентьєва К.Г.
Харків 2010
Исходные данные
Экспериментально получены результаты серии наблюдений напряжения U постоянного размера. Результаты наблюдений считаются независимыми и равноточными (по условиям эксперимента). В общем случае они могут содержать систематическую и случайную составляющие погрешности измерений. Указана доверительная вероятность P=0,95 результата измерения.
Задание
По результатам многократных наблюдений определить наиболее достоверное значение измеряемой физической величины и его доверительные границы.
Таблица 1
| U(1)=170.02 | U(17)=170.20 |
| U(2)=170.41 | U(18)=170.30 |
| U(3)=169.95 | U(19)=169.59 |
| U(4)=170.17 | U(20)=169.95 |
| U(5)=169.95 | U(21)=169.77 |
| U(6)=170.01 | U(22)=169.84 |
| U(7)=170.26 | U(23)=169.95 |
| U(8)=190.23 | U(24)=159.84 |
| U(9)=169.84 | U(25)=170.33 |
| U(10)=169.73 | U(26)=169.73 |
| U(11)=169.74 | U(27)=169.91 |
| U(12)=170.21 | U(28)=170.35 |
| U(13)=169.76 | U(29)=170.20 |
| U(14)=169.67 | U(30)=169.88 |
| U(15)=169.83 | U(31)=169.60 |
| U(16)=170.35 | U(32)=170.50 |
Доверительная вероятность: P= 0, 99
Доверительные границы: ![]()
Разрядность: 5 разрядов*![]()
Количество наблюдений: n = 32
Обработка результатов измерений
Анализируем серию наблюдений на наличие промахов. Если они имеются, то их необходимо исключить из дальнейшей обработки.
При анализе обнаружен один промах U(8)=190.23 и U(24)=159.84 (В). Исключим его из результатов измерений.
Таблица 2
| U(1)=170.02 | U(16)=170.20 |
| U(2)=170.41 | U(17)=170.30 |
| U(3)=169.95 | U(18)=169.59 |
| U(4)=170.17 | U(19)=169.95 |
| U(5)=169.95 | U(20)=169.77 |
| U(6)=170.01 | U(21)=169.84 |
| U(7)=170.26 | U(22)=169.95 |
| U(8)=169.84 | U(23)=170.33 |
| U(9)=169.73 | U(24)=169.73 |
| U(10)=169.74 | U(25)=169.91 |
| U(11)=170.21 | U(26)=170.35 |
| U(12)=169.76 | U(27)=170.20 |
| U(13)=169.67 | U(28)=169.88 |
| U(14)=169.83 | U(29)=169.60 |
| U(15)=170.35 | U(30)=170.50 |
Проверим соответствие экспериментального закона распределения нормальному закону.
Для этого используем составной критерий согласия. Он включает в себя два независимых критерия, их обозначают I и II. Первый из этих критериев (критерий I) обеспечивает проверку соответствия распределения экспериментальных данных нормального закона распределения вблизи центра распределения, а второй критерий (критерий II) – на краях распределения. Если при проверке не удовлетворяется хотя бы один из этих критериев, то гипотеза о нормальности распределения результатов наблюдений отвергается.
Для проверки гипотезы о нормальности распределения исходной серии результатов наблюдений по критерию I вычисляют параметр d, определяемый соотношением:
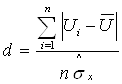 (1),
(1),
где ![]()
![]() (В) – среднее
арифметическое результатов наблюдений Ui ,
(В) – среднее
арифметическое результатов наблюдений Ui , ![]() ;
;
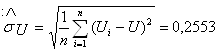 (В) – смещённая оценка СКО результатов наблюдений Ui,
(В) – смещённая оценка СКО результатов наблюдений Ui,
![]() .
.
Для облегчения дальнейших расчетов сведём значения ![]()
![]() и
и
![]() в таблицу:
в таблицу:
Таблица 3
| i |
|
|
|
| 1. | 0.02 | 0.0004 | 0.02 |
| 2. | 0.41 | 0.1681 | 0.41 |
| 3. | -0.05 | 0.0025 | 0.05 |
| 4. | 0.17 | 0.0289 | 0.17 |
| 5. | -0.05 | 0.0025 | 0.05 |
| 6. | 0.01 | 0.0001 | 0.01 |
| 7. | 0.26 | 0.0676 | 0.26 |
| 8. | -0.16 | 0.0256 | 0.16 |
| 9. | -0.27 | 0.0729 | 0.27 |
| 10. | -0.26 | 0.0676 | 0.26 |
| 11. | 0.21 | 0.0441 | 0.21 |
| 12. | -0.24 | 0.0576 | 0.24 |
| 13. | -0.33 | 0.1089 | 0.33 |
| 14. | -0.17 | 0.0289 | 0.17 |
| 15. | 0.35 | 0.1225 | 0.35 |
| 16. | 0.20 | 0.04 | 0.20 |
| 17. | 0.30 | 0.09 | 0.30 |
| 18. | -0.41 | 0.1681 | 0.41 |
| 19. | -0.05 | 0.0025 | 0.05 |
| 20. | -0.23 | 0.0529 | 0.23 |
| 21. | -0.16 | 0.0256 | 0.16 |
| 22. | -0.05 | 0.0025 | 0.05 |
| 23. | 0.33 | 0.1089 | 0.33 |
| 24. | -0.27 | 0.0729 | 0.27 |
| 25. | -0.09 | 0.0081 | 0.09 |
| 26. | 0.35 | 0.1225 | 0.35 |
| 27. | 0.20 | 0.04 | 0.20 |
| 28. | -0.12 | 0.0144 | 0.12 |
| 29. | -0.4 | 0.16 | 0.4 |
| 30. | 0.5 | 0.25 | 0.5 |
|
|
|
|
Рассчитаем параметр d в соответствии с формулой (1):
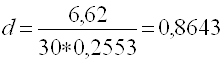
Результаты наблюдений Ui считаются распределёнными по нормальному закону, если выполняется следующее условие
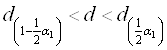 ,
,
где ![]() ,
, ![]() - квантили распределения
параметра d. Их находят по таблице П.1 α-процентных точек распределения
параметра d по заданному объёму выборки n и принятому для критерия I уровню
значимости α1. Выберем α1 и α2
из условия α≤α1+α2, где
α=1-Р=1-0,99=0,01.
- квантили распределения
параметра d. Их находят по таблице П.1 α-процентных точек распределения
параметра d по заданному объёму выборки n и принятому для критерия I уровню
значимости α1. Выберем α1 и α2
из условия α≤α1+α2, где
α=1-Р=1-0,99=0,01.
α1=0,02 и α2=0,01.
Для n=15,р=0,95, α=0,02
![]()
![]()
a)Для n=30,P=0.99 ![]() .
.
|
|
0.8901 |
| 30 | У |
| 31 | 0.8827 |
Проведём интерполяцию:
Y(d )=0.8901+0.8(0.8827-0.8901)=0.8901-0.0059=0.8842
Для n=30,P=0.99
|
|
0.7040 |
| 30 | У |
| 31 | 0.7110 |
Проведём интерполяцию:
Y( )=0,7040+0,8(0,7110-0,7040)=0,7040+0,0056=0,7096
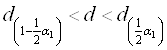
0,7096<0,8643<0,8842
Распределение результатов наблюдений соответствует критерию I.
По критерию II, распределение результатов наблюдений
соответствует нормальному закону распределения, если не более m разностей ![]() превзошли значение
превзошли значение
![]() ,
,
где 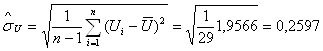 (В) –
несмещенная оценка СКО результатов наблюдений Ui;
(В) –
несмещенная оценка СКО результатов наблюдений Ui;
![]() - верхняя квантиль распределения интегральной функции
нормированного нормального распределения, соответствующая доверительной
вероятности Р2. Значение m и Р2 находим по числу
наблюдений n и уровню значимости α2 для критерия II по таблице
П.2 приложения. m=2, Р2=0,99. Затем вычисляем:
- верхняя квантиль распределения интегральной функции
нормированного нормального распределения, соответствующая доверительной
вероятности Р2. Значение m и Р2 находим по числу
наблюдений n и уровню значимости α2 для критерия II по таблице
П.2 приложения. m=2, Р2=0,99. Затем вычисляем:
![]()
По таблице П.3 приложения интегральной функции нормированного
нормального распределения находят ![]() ,
соответствующее вычисленному значению функции Ф(
,
соответствующее вычисленному значению функции Ф(![]() ):
при Ф(
):
при Ф(![]() )=0,995;
)=0,995;![]() =2,82;
=2,82;
![]() =2,82*0,2597=0,7323 (В).
=2,82*0,2597=0,7323 (В).
Ни одно значение ![]() не
превосходит величину
не
превосходит величину ![]() , следовательно
распределение результатов наблюдений удовлетворяет и критерию II, поэтому
экспериментальный закон распределения соответствует нормальному закону.
, следовательно
распределение результатов наблюдений удовлетворяет и критерию II, поэтому
экспериментальный закон распределения соответствует нормальному закону.
Проведём проверку грубых погрешностей результатов наблюдений (оценки анормальности отдельных результатов наблюдений). Для этого:
а) Составим упорядоченный ряд результатов наблюдений, расположив исходные элементы в порядке возрастания, и выполним их перенумерацию:
Таблица 4
| U(1)=169.59 | U(16)=169.95 |
| U(2)=169.60 | U(17)=169.95 |
| U(3)=169.67 | U(18)=170.01 |
| U(4)=169.73 | U(19)=170.02 |
| U(5)=169.73 | U(20)=170.17 |
| U(6)=169.74 | U(21)=170.20 |
| U(7)=169.76 | U(22)=170.20 |
| U(8)=169.77 | U(23)=170.21 |
| U(9)=169.83 | U(24)=170.26 |
| U(10)=169.84 | U(25)=170.30 |
| U(11)=169.84 | U(26)=170.33 |
| U(12)=169.88 | U(27)=170.35 |
| U(13)=169.91 | U(28)=170.35 |
| U(14)=169.95 | U(29)=170.41 |
| U(15)=169.95 | U(30)=170.50 |
б) Для крайних членов упорядоченного ряда U1 и U15,
которые наиболее удалены от центра распределения (определяемого как среднее
арифметическое Ū этого рядя) и поэтому с наибольшей вероятностью могут
содержать грубые погрешности, находим модули разностей ![]() =
=![]() (В) и
(В) и ![]() =
=![]() (В), и для большего из них
вычисляем параметр:
(В), и для большего из них
вычисляем параметр:
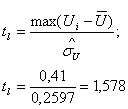
в) Для n=30, ![]()
![]() из таблицы 4 определим
из таблицы 4 определим ![]() =3,071.
=3,071.
Так как ti< tT, поэтому грубых результатов нет.
Вычислим несмещенную оценку СКО результата измерения в соответствии с выражением:
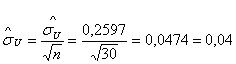 (В).
(В).
Определим доверительные границы ![]() случайной
составляющей погрешности измерений с многократными наблюдениями в зависимости
от числа наблюдений n 30 в выборке, не содержащей анормальных результатов, по
формуле:
случайной
составляющей погрешности измерений с многократными наблюдениями в зависимости
от числа наблюдений n 30 в выборке, не содержащей анормальных результатов, по
формуле: ![]() , где Z– коэффициент по
заданной доверительной вероятности Р=0,99 ; Z =2,58
, где Z– коэффициент по
заданной доверительной вероятности Р=0,99 ; Z =2,58
![]()
![]() (В).
(В).
Определим доверительные границы ![]() суммарной
не исключённой систематической составляющей погрешности результатов измерений с
многократными наблюдениями:
суммарной
не исключённой систематической составляющей погрешности результатов измерений с
многократными наблюдениями:
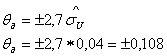 (В).
(В).
Определим доверительные границы ![]() суммарной
(полной) погрешности измерений с многократными наблюдениями.
суммарной
(полной) погрешности измерений с многократными наблюдениями.
Так как 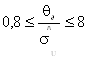 , тогда
, тогда
![]()
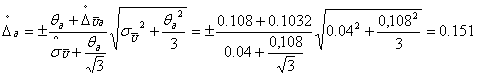 В.
В.
Запишем результат измерений с многократными наблюдениями:
U= (170,000±0,151) В; Р=0,99