Курсовая работа: Расчет и обоснование привода

1. Кинематический и силовой расчет привода

1.1 Выбор электродвигателя

Общий коэффициент полезного действия привода

где h_общ – общий КПД привода

h_м1 – КПД упругой муфты, h_м1 = 0,99;

– КПД конической передачи, h_кон = 0,97

h_цп – КПД зубчатой цилиндрической передачи, h_цп = 0,975;

h_м2 – КПД упругой муфты, h_м2 = 0,99;

h_оп – КПД подшипников качения, h_оп = 0,99

Примечание: значение КПД см. [Журнал лабораторных работ, табл. 2]

Мощность на рабочем органе

Частота вращения рабочего органа

Потребная частота вала электродвигателя

где: u_Т=3 – значение передаточного числа тихоходной ступени цилиндрической передачи;

u_Б=5 – значение передаточного числа быстроходной ступени ступени цилиндрической передачи.

1.2 Определение общего передаточного числа привода и разбивка его по ступеням, из условия получения минимальных габаритов

Общее передаточное число привода

Передаточное число редуктора

т. к. отсутствуют ременная и цепная передачи

Передаточное число тихоходной ступени редуктора

Передаточное число быстроходной ступени редуктора

Принятое передаточное число редуктора

Принимаем стандартные значения U_б=3.55 и U_т=5 [Журнал лабораторных работ, табл. 6]

Относительная погрешность передаточного числа редуктора

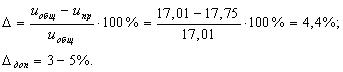
2. Проектирование редуктора

2.1 Тихоходная ступень

Выбор материала и термической обработки

Принимаем:

Колесо – Ст 45 улучшение; HB₄ 240…285;

Шестерня – Ст 40Х улучшение; HB₃ 260…280;

Примечание: марки материалов и рекомендуемые твёрдости см. [Журнал лабораторных работ, табл10]

Допускаемые контактные напряжения при расчете на контактную выносливость

Эквивалентное время работы

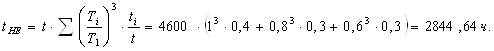
Эквивалентное число циклов нагружения

для колеса

для шестерни

Базовое число циклов нагружения

для колеса

для шестерни

Коэффициенты долговечности:

для колеса ,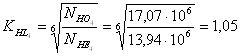

для шестерни  

Базовый предел контактной выносливости

для колеса

для шестерени

Смотри [Журнал лабораторных работ, табл 11]

Допускаемые контактные напряжения

для колеса

для шестерни

S_H=1.1 коэффициент безопасности, см. [Журнал лабораторных работ, табл. 11]

Расчетное допускаемое напряжение

т. к. , то

Допускаемые напряжения изгиба при расчете на изгибную выносливость (усталость)

Эквивалентное время работы

при HB_ср<350

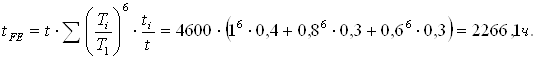
Эквивалентное число циклов нагружения

для колеса

для шестерни

Коэффициенты долговечности:

для колеса ,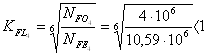

для шестерни  т. к.

Базовый предел изгибной выносливости

для колеса

для шестерни

Примечание: см. [Журнал лабораторных работ, табл. 11]

Допускаемые напряжения изгиба при расчете на усталость

для колеса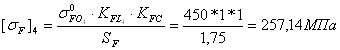

для шестерни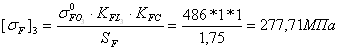

S_F=1.75-коэффициент безопасности, см. [Журнал лабораторных работ, табл. 11]

где K_FC=1 – коэффициент реверсивности.

Допускаемые напряжения для проверки прочности зубьев при перегрузках

Допускаемые контактные напряжения при перегрузках моментом Т_max.

для колеса

для шестерни

Допускаемые напряжения изгиба при перегрузках моментом Т_max.

для колеса

для шестерни

Межосевое расстояние

Межосевое расстояние косозубой тихоходной ступени из условия контактной выносливости

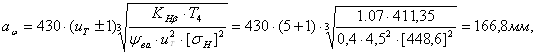
 см. [Балдин, Галевко; стр. 37; табл 2.3]

 см. [Балдин, Галевко; стр. 30; рис 2,11]

Округляем до стандартного значения a_ω=160 мм., См. [Журнал лабораторных работ, табл. 9]

Нормальный модуль

 См. [Журнал лабораторных работ, табл. 9]

Принимаем по ГОСТу m=2,5.

Число зубьев для косозубой передачи тихоходной ступени

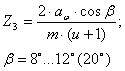
Принимаем:

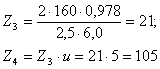
Уточняем угол наклона зубьев:

β=arccosβ=10^° 8^' 30.46^»

Действительное передаточное число

Относительная погрешность

Делительные диаметры шестерни и колес

Диаметр окружности выступов

для шестерни

для колеса

Диаметры окружности впадин

для шестерни

для колеса

Ширина зубчатых колес

для колеса

для шестерни

Определение слабого элемента при расчете на изгибную выносливость.

Эквивалентное число зубьев:

Коэффициент формы зуба:

Приложение: См. [Балдин, Галевко; стр. 43; рис 2.13]

Сравниваем:

Вывод: слабым элементом является зуб колеса, т.е. расчет на изгибную выносливость необходимо вести по колесу, [σ_F]₄=257,14 МПа.

Определение расчетной нагрузки.

Удельная нагрузка на единицу длины зуба:

 см. [Балдин, Галевко; стр. 33; Табл 2.2]

Примечание: см. [Балдин, Галевко; Стр. 30,32; рис 2.11, Табл 2.1]

Определение действующих напряжений изгиба для зуба колеса.

 МПа

y_β=cosβ – коэффициент, учитывающий наклон зуба;

Коэффициент, учитывающий перекрытие зубьев:

Вывод:  следовательно работоспособность по изгибной выносливости обеспечена.

Проверочный расчет зубьев на контактную выносливость.

Определение окружной скорости в зацеплении и степени точности передачи

Принимаем 9 степень точности.

Определение расчетной нагрузки при расчете на контактную выносливость.

 – коэффициент распределения между зубьями.

см. [Балдин, Галевко; стр. 33; Табл 2.2]

 – коэффициент динамической нагрузки.

Примечание: см. [Балдин, Галевко; Стр. 30,32; рис 2.11, Табл 2.1]

Определение действующих контактных напряжений.

Коэффициент, учитывающий геометрию передачи – Z_H= Z_м=275 МПа – коэффициент, учитывающий свойства материала.

Коэффициент, учитывающий суммарную длину контактных линий, где: К_ε=0,95

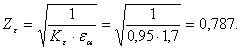
Вывод: σ_H=438,69 МПа ≤ [σ_H]=448,6 МПа, работоспособность зубчатой передачи по контактной выносливости обеспечена.

Проверочный расчет зубьев при перегрузках

Расчет ведется по T_max в момент пуска, T_max/T_ном=2,4 из характеристики двигателя.

Контактные напряжения в момент пуска:

Вывод: σ_Hmax=694,99 МПа ≤ [σ_H]_max3=1624 МПа, контактная прочность рабочей поверхности зуба при перегрузках обеспечена.

Напряжения изгиба в период пуска:

Вывод: σ_Fmax=176,88 МПа ≤ [σ_F]_max3=685 МПа, изгибная прочность зуба при перегрузках обеспечена.

2.2 Расчёт конической быстроходной передачи

Принимаем для конической передачи на быстроходной ступени передачу с круговым зубом при β=30⁰ и проводим проектировочный расчет, определяя делительный диаметр шестерни в среднем сечении при коэффициентах К_d=600; Z_M=275 МПа; К_bL=b/R_L=0.285, θ_н=1.25 коэффициент нагрузки при круговом зубе.

=1.07 см. [Балдин, Галевко; стр. 66; рис 3,7]

Число зубьев шестерни Z₁=19 и Z₂=19*3,55=67

Приложение: см. [Балдин, Галевко; стр. 68; рис 3,8]

Определим модуль в среднем сечении

Принимаем стандартное значение m_nm=2, тогда новые значения составляют

d_m1=m_nm*Z1/cos β₁=2*19/0.867=43,83 мм

d_m2=m_nm*Z2/cos β₁=2*67/0.867=154,56 мм

m_te=m_nm/(cos β₁*(1–0.5*K_bL))=2/(0.886*(1–0.5*0.285))=2.69 мм

диаметры делительных конусов на внешнем торце конической ступени

d_e1=2.69*19=51.11 мм

d_e2=2.69*67=180,23 мм

d_a1=d_e1+2m_te=51.11+2*2.69=56.49 мм

d_a2=d_e2+2m_te=180.23+2*2.69=185.61 мм

Проверим отсутствие пересечения вала III с колесом Z2 при межосевом расстоянии a_w=160 мм. Минимальный диаметр вала III

d=(Т_ш1000/(0,2 [τ_кр])^0.33=(1000*544/(0.2*25))^0.33=47.7

d_a2/2+47.7/2=185.61/2+24=116.80<160 т.е. колесо Z2 не пересекает вал III

Конусное расстояние R_l=0.5m_te*(Z₁²+Z₂²)^0.5=0.5*2*(19²+67²)^0.5=69.64 мм

Ширина колеса b_w=R_l*K_bl=69.64*0.285=19.85 мм→20 мм

Угол делительного конуса шестерни δ₁=arctg (Z1/Z2)=arctg (19/67)=15⁰49`

δ₂=90 – δ₁=74⁰10`

2.3 Проверочный расчёт на изгибную выносливость быстроходной ступени

Определение слабого элемента контактирующих колёс

Имеем Z₁=19, cosβ=0.867, Z₂=67

Эквивалентное число зубьев:

Z_v1=Z₁/(cos³β*cosδ₁)=19/(0.867³*0.97)=30.06

Коэффициент формы зуба Y_f4=3.95 при X=0

Приложение см. [Балдин, Галево; стр. 43; рис 2,13]

При Z₂=67 эквивалентное число зубьев

Z_v2=Z₂/(cos³β*cosδ₂)=67/(0.867³*0,243)=423,07

Коэффициент формы зуба Y_f4=3.79 при Х=0

Сравним [σ_F]₁/Y_F1 и [σ_F]₂/Y_F2; 278/3,95=70,4>259/3.79=68.3

Вывод: слабым элементом является зуб колеса, поэтому расчёт изгибной выносливости ведём по зубу колеса [σ_F]₂=259 МПа

Определение расчётной нагрузки при расчёте на изгибную выносливость

ν_F=0.94+0.08*U_б=0,94+0,08*3.55=1.224 коэффициент нагрузочной способности для конических передач с круговым зубом;

K_Fβ=1.103 при Ψ_bl=0.590

K_FV= 1,11 при HB<350, V=3.83 м/с, и 8 ой степени точности

K_Fα=1.22

Определение действующих напряжений изгиба для зуба колеса.

 МПа

y_β=cosβ – коэффициент, учитывающий наклон зуба;

Коэффициент, учитывающий перекрытие зубьев:

Определение коэффициента торцевого перекрытия.

Вывод: σ_F2=81.39 МПа ≤ [σ_H]=259 МПа, работоспособность зубчатой передачи по изгибной выносливости обеспечена.

Проверочный расчет зубьев при перегрузках.

Расчет ведется по T_max в момент пуска, T_max/T_ном=2,4 из характеристики двигателя.

Контактные напряжения в момент пуска:

Вывод: σ_Hmax=848 МПа ≤ [σ_H]_max3=1260 МПа, контактная прочность рабочей поверхности зуба при перегрузках обеспечена.

Напряжения изгиба в период пуска:

Вывод: σ_Fmax=195.3 МПа ≤ [σ_F]_max3=685 МПа, изгибная прочность зуба при перегрузках обеспечена.

2.4 Расчёт конической передачи на контактную выносливость

Удельное окружное усилие

K_Hβ=1.07 см. [Балдин, Галевко; стр. 66; рис 3.7]

K_HV= 1,04 при HB<350, V=3.83 м/с, и 8 ой степени точности

K_Hα=1.07

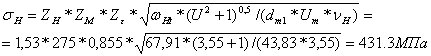
Коэффициент сопряжения формы поверхности зуба

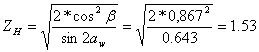
Для α _w=20⁰

Z_H=1.76*cosβ=1,76*0,867=1,52

Z_м=275 МПа, для стальных колёс

Вывод: σ_H=431,3 МПа ≤ [σ_H]=448,6 МПа, работоспособность зубчатой передачи по контактной выносливости обеспечена.

3. Расчёт валов на кручение. Предварительный выбор подшипников

3.1 Условия прочности на кручение

τ_кр=T_кр/W_p<[τ_кр]=0.25*360=90 МПа для стали 45 (III вал)

валы I и II сталь 40Х σ_т=640 МПа не учитывая действие изгибающих моментов, принимаем для валов [τ_кр]=(20…25) МПа,

d_вI≥(Т₁*10³/(0,2*[τ_кр]))^0.33=(24,99*10³/(0,2*20))^0,33=17,89 мм

принимаем с учётом диаметра вала двигателя d=28 мм, и с дообработкой МУВП-25

диаметр входного участка ведущего вала под полумуфту d_в1=25 мм, тогда участок вала под крышку подшипника для упора полумуфты 25+6=32 мм. Под подшипник I вала принимаем диаметр d_в1п=35 мм.

d_вII≥(Т₂*10³/(0,2*[τ_кр])^0.33=(85,61*10³/(0,2*20))^0,33=26,86 мм

Принимаем диаметр промежуточного вала под подшипником d_в2=35 мм

d_вIII≥(Т₃*10³/(0,2*[τ_кр])^0.33=(417,28*10³/(0,2*20))^0,33=45.3 мм

Принимаем диаметр тихоходного вала под подшипником d_в3=50 мм

Усилия в зацеплении на быстроходной ступени

Окружное усилие Pt₁₂=2*T_II*10³/d_m2=2*85.61*1000/154.56=1107 H

Радиальное усилие Pr₁=Pt₁₂/cosβ₁*(tgα*cosδ₁-sin β₁*sin δ₁)=273 H

Осевое усилие Pa₁=Pt₁₂/ cosβ₁*(tgα*cosδ₁+sin β₁*sin δ₁)=622 H

Усилия в зацеплении на тихоходной ступени

Угол наклона линии зацепления α=20⁰

Угол наклона зуба β_3,4=10⁰8`30``, Z3-левый зуб

Окружное усилие Pt₃₄=2*T_II*10³/d₃=2*85.61*1000/53.35=3209 H

Радиальное усилие Pr₃₄=Pt₃₄*tgα/cos β₃=1186 H

Осевое усилие Pa₃₄=Pt₃₄*tgβ₃=573 H

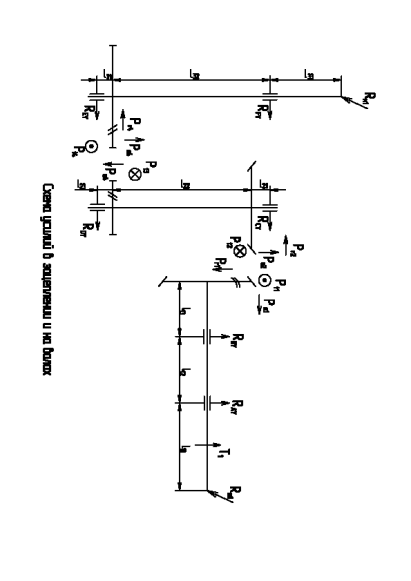
4. Схема сил и усилий в зацеплении

R_m1=2940*0.100=294.0 [H]

R_m2=2*31.25/0.210=297.6 [H]

l₁₁=91 [мм] l₂₁=50 [мм] l₃₁=51 [мм]

l₁₂=48 [мм] l₂₂=95 [мм] l₃₂=137 [мм]

l₁₃=19 [мм] l₂₃=30 [мм] l₃₃=80 [мм]

d₁=43.83 [мм]; d₂=154.86 [мм]; d₃=53,35 [мм]; d₄=277,67 [мм]

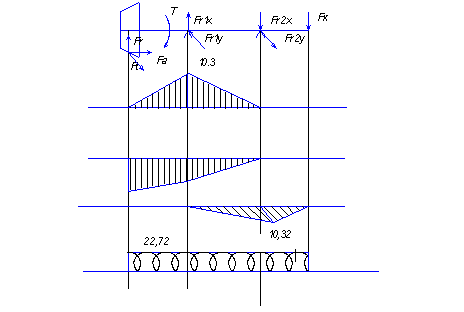
5. Расчёт быстроходного вала

Марка стали тихоходного вала – Сталь 40ХН.

Проверку статической прочности выполняют в целях предупреждения пластических деформаций в период действия кратковременных перегрузок.

В расчете используется коэффициент перегрузки

К_п = Т_max/Т,

где Т_max - максимальный кратковременно действующий вращающий момент (момент перегрузки),

Т – номинальный (расчетный) вращающий момент.

Для выбранного ранее двигателя К_п = 2,2.

По рассчитанным ранее реакциям в опорах и известных силах, действующих на валах строим эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях, и эпюру крутящего момента. Данные эпюры были приведены ранее, при определении реакций в опорах подшипников.

В расчете определяют нормальные s и касательные t напряжения в рассматриваемом сечении вала при действии максимальных нагрузок:

При анализе эпюры изгибающих моментов, приходим к выводу, что нас интересуют 2 сечения, представляющих опасность, оценку их значимости будем производить по величинам нормальных и касательных напряжений, т. к. имеем разные моменты сопротивления.

В расчете определяют нормальные s и касательные t напряжения в рассматриваемом сечении вала при действии максимальных нагрузок:

s = 10³*M_max / W + F_max / A,

t = 10³*M_kmax/W_k,

где M_max = К_п*М_к = 30,08*2,2 = 66,19 Нм.

F_max = К_п*Fa = 2,2*1179 = 2594 Н.

W = p*d³/32 = 4209 мм³,

W_k = 2*W = 8418 мм³.

А = p*d²/4 = 962,1 мм².

s = 10³*66,19/4209 + 2594/962,1 = 8,42 МПа,

s = 8,42 МПа.

М_kmax = К_п*Т = 2,2*23 = 50,6 Нм.

t = 10³*50,6/8418 = 6 МПа.

t = 6 МПа.

Рассчитаем частные коэффициенты запаса прочности по нормальным и касательным напряжениям:

S_тs = s_т/s, s_т = 640 МПа.

S_тt = t_т/t, t_т = 380 МПа.

S_тs = 640/8,42 = 76

S_тt = 380/6 = 63,22

Общий коэффициент запаса прочности по пределу текучести при совместном действии нормальных и касательных напряжений:

S_т = S_тs*S_тt/(S_тs² + S_тt²)^1/2 ³ [S_т] = 1,3…2

S_т = S_тs*S_тt/(S_тs² + S_тt²)^1/2 = 48,6

Получили, что

S_т = 48,6 ³ [S_т] = 1,3…2

5.1 Расчёт тихоходного вала

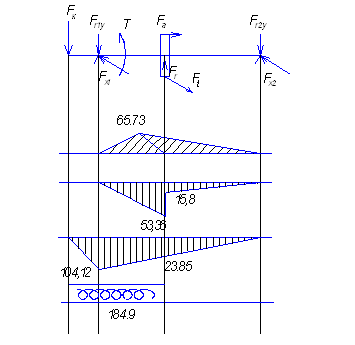
s = 10³*M_max / W + F_max / A,

t = 10³*M_kmax/W_k,

где M1_max = К_п*М = 108,5*2,2 = 238,7 Нм.

F1_max = К_п*Fa = 2,2*484,5 = 1066 Н.

W = p*D³ /32, – сечение круглое для контактной поверхности колеса и вала.

где D1 = 40 мм,

W1 = 6283,2 мм³

W1_k = 2*W = 12566,4 мм³.

А = p*d²/4,

A1 = 1256,6 мм²

s1 = 38,8 МПа.

М_kmax = К_п*Т = 2,2*184,9 = 407 Нм.

t 1= 32,4 МПа.

Переходим к рассмотрению следующего сечения:

где M2_max = К_п*М2 = 229 Нм.

F2_max = К_п*F2a = 1066 Н.

W = p*D³ /32, – сечение круглое для контактной поверхности колеса и вала.

где D2 = 35 мм,

W2 = 4209,25 мм³

W2_k = 2*W = 8418,5 мм³.

А = p*d²/4,

A2 = 962,1 мм²

s1 = 55,5 МПа.

М_kmax = К_п*Т = 2,2*184,9 = 407 Нм.

t 2= 48,3 МПа.

Оценивая нагруженность участков, приходим к выводу, что наиболее нагружен участок вала под первой опорой подшипника.

Рассчитаем частные коэффициенты запаса прочности по нормальным и касательным напряжениям:

S_тs = s_т/s, s_т = 540 МПа.

S_тt = t_т/t, t_т = 290 МПа.

S_тs = 540/55,5 = 9,7

S_тt = 290/48,3 = 6

Общий коэффициент запаса прочности по пределу текучести при совместном действии нормальных и касательных напряжений:

S_т = S_тs*S_тt/(S_тs² + S_тt²)^1/2 ³ [S_т] = 1,3…2

S_т = S_тs*S_тt/(S_тs² + S_тt²)^1/2 = 9,7*6/(9,7² + 36)^1/2 = 5,11

Получили, что

S_т = 5,11 ³ [S_т] = 1,3…2

6. Предварительный расчёт подшипников тихоходного вала

Наиболее нагруженная опора тихоходного вала имеет R_e=2257.8 [Н], Р_а=573 [Н], n=80.56 об/мин

Проверим шарикоподшипник №207

Динамическая грузоподъёмность C_r=34000 [H]

Статическая грузоподъёмность C₀=25600 [H]

V=1 т. к. вращается внутреннее кольцо

Х=0,56, Y=2.53

Вычислим эквивалентную динамическую радиальную нагрузку

Pe=(V*X*F_r+Y*Pa) K_б*K_т=(1*0.56*2257.88+2.53*573)*1.25*1=4634.5 [H]

Кт=1, Коэффициент учитывающий рабочую температуру редуктора, у нас она <100 C⁰

K_б=1.25 Коэффициент безопасности

Требуемая динамическая грузоподъёмность

L_10h=2844.6 [Н] долговечность подшипника

n – частота вращения тихоходного вала

Cтр=<Cr, следовательно подшипник пригоден.

7. Расчёт упругой муфты с торообразной оболочкой

При передаче момента в оболочке возникают касательные напряжения крутильного сдвига, которые достигают большего значения в сечении диаметра D1=204 мм

Тк – момент передаваемый муфтой