Контрольная работа: Виды передаточной характеристики

Контрольная работа по дисциплине "Автоматика и управление"

Вариант 1 - РС-711511.

Вид передаточной характеристики:

Входное воздействие:

Структурная схема звена имеет вид:

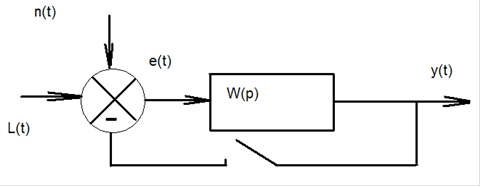
Записать передаточные функции системы в замкнутом и разомкнутом состоянии и определить устойчивость.

Передаточная функция системы в замкнутом виде записывается в виде:

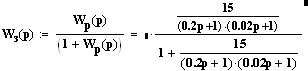
Предполагается, что система автоматики может находиться в двух состояниях - устойчивом и неустойчивом.

Устойчивость системы определяем по критерию Гурвица.

Для этого составляем характеристическое уравнение с учётом передаточной функции системы в разомкнутом состоянии в виде:

И так как левое выражение имеет дробно-рациональный вид, то, приравняв к нулю числитель выражения, стоящий в левой части, перепишем его в виде:

Это выражение равно нулю, если:

 или

Для оценки устойчивости системы радиоавтоматики необходимо вычислить определитель Гурвица. Составим матрицу Гурвица:

Система радиоавтоматики устойчива.

Построить переходную характеристику системы в замкнутом состоянии и определить перерегулирование в системе.

Переходной характеристикой называется реакция системы на воздействие на неё единичного сигнала:

, где  

Разложим эту дробь в сумму обыкновенных дробей:

Домножаем числители каждой дроби на :

Группируем множители:

Получаем систему уравнений:

Решением этой системы уравнений являются следующие значения:

Таким образом,

Домножаем на 1000 элементы второй дроби:

"Делим" числитель второй дроби, чтобы избавиться от суммы ():

Преобразуем множители к виду функционального преобразования Лапласа:

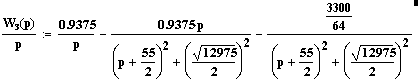
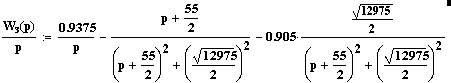
Воспользуемся формулами обратных преобразований Лапласа:

, ,

Получаем следующее выражение для переходной характеристики:

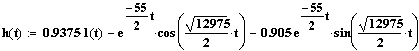
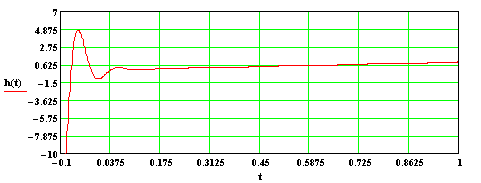
По графику переходной характеристики необходимо определить величину перерегулирования γ.

Установившееся значение выходного сигнала системы вычисляется следующим образом:

,

где  - передаточная характеристика системы в замкнутом состоянии.

Перерегулирование γ равно отношению максимального значения выходного сигнала в переходном процессе к установившемуся значению:

Определить динамическую ошибку при входном воздействии λ (t).

Динамической ошибкой называется ошибка в установившемся режиме работы системы при действии на неё нестационарного сигнала.

Значение динамической ошибки при входном воздействии λ (t) определяется по формуле:

где Ci - коэффициенты ошибки от воздействия λ (t), которые находятся по формулам:

, при p=0,

,

где We - передаточная функция ошибки, которая вычисляется по формуле:

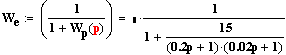
Найдем производную передаточной функции ошибки:

Подставив в производную значение p=0, получаем:

Найдём : ,

Подставив полученные значения коэффициентов и производных в формулу, получим: