Курсовая работа: Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца

Министерство образования и науки республики Казахстан

Северо-Казахстанский государственный университет

им. М. Козыбаева

Факультет информационных технологий

Кафедра математики

Курсовая работа

"Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца"

Петропавловск, 2007


Аннотация

В данной курсовой работе исследованы свойства некоторых семейств конечномерных пространств и доказаны интерполяционные теоремы для этих классов пространств.


Содержание

Введение

1. Основные понятия и некоторые классические теоремы теории интерполяции

2. Общие свойства интерполяционных пространств

3. О норме и спектральном радиусе неотрицательных матриц

4. Некоторые интерполяционные свойства семейств конечномерных пространств

Заключение

Список использованной литературы


Введение

Теория интерполяции функциональных пространств как самостоятельная ветвь функционального анализа сформировалась за последние 40-45 лет. Она играет все возрастающую роль в анализе и его приложениях. Центральной темой теории является проблема интерполяции линейных операторов. Эта проблема тесно связана с задачей построения совокупности "промежуточных" пространств – арены, на которой действуют "промежуточные" операторы. Основополагающий вклад в теорию был сделан Эл.-Л. Лионсом, А.П. Кальдероном и С.Г. Крейном. При этом не следует, конечно, забывать, что исследованием названных авторов предшествовали (и стимулировали их) классические теоремы Рисса и Марцинкевича об интерполяции линейных операторов в пространствах lp.

Теория интерполяция также применяется в других областях анализа (например, в теории уравнений с частными производными, численном анализе, теории аппроксимации). Рассматривают два существенно различных интерполяционных метода: метод вещественной интерполяции и метод комплексной интерполяции. Модельными примерами для этих методов служат доказательства теоремы Марцинкевича и теоремы Рисса-Торина соответственно. Один из самых ранних примеров интерполяции линейных операторов был предложен Шуром. Шур сформулировал свой результат для билинейных форм, или вернее для матриц, соответствующих этим формам. В 1926 году М. Рисс доказал первую версию теоремы Рисса-Торина с ограничением p≤q, которое как он показал, существенно в случае, когда в качестве скаляров берутся вещественные числа. Основным рабочим инструментом Рисса было неравенство Гельдера. Но в 1938 году Торин привел совершенно новое доказательство и смог устранить ограничение p≤q. В то время как Рисс пользовался вещественными скалярами и неравенством Гельдера, Торин использовал комплексные скаляры и принцип максимума.


1. Основные понятия и некоторые классические теоремы теории интерполяции

Пусть (u,μ) – пространство с мерой μ, которую будем всегда предполагать положительной. Две рассматриваемые функции будем считать равными, если они отличаются друг от друга лишь на множестве нулевой μ-меры. При этом обозначим через lp(u,dμ) или просто (lp(dμ), lp(u) или lp) лебегово пространство всех скалярнозначных μ-измерных функций f и u, для которых величина

конечна, здесь 1≤p<∞.

В случае, когда p=∞, пространство lp состоит из всех μ-измеримых ограниченных функций. В этом случае

Пусть T - линейное отображение пространства lp=lp(u,dμ) в пространство lq=lq(v,dν). Это означает, что T(αf+βg)=αT(f)+βT(g).

Если к тому же T- ограниченное отображение, то есть если величина конечна, то пишут T: lp®lq.


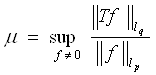
Число μ называется нормой отображения T. Справедливы следующие известные теоремы:

Теорема 1.1 (интерполяционная теорема Рисса-Торина)

Предположим, что   и что T:  с нормой μ0 и T :  с нормой μ1.

Тогда T: →  с нормой μ, удовлетворяющей неравенству  (*), при условии, что 0<θ<1 и ;  .

Неравенство (*) означает, что μ как функция от θ логарифмически выпукла, то есть lnμ – выпуклая функция.

Доказательство теоремы приведено в [1].

Для скалярнозначной μ-измерной функции f, принимающей почти всюду конечные значения, введем функцию распределения m(σ,f) по формуле

Ясно, что m(σ,f) представляет собой вещественнозначную функцию от σ, определенную на положительной вещественной полуоси . Очевидно, что m(σ,f) – невозрастающая и непрерывная справа функция. Кроме того,

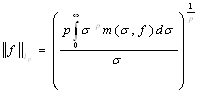 при 1≤p<∞

и .


Используя функцию распределения m(σ,f), введем теперь слабые lp-пространства, обозначаемые через . Пространства , 1≤p<∞, состоит из всех функций f , таких что

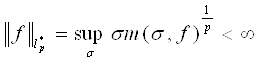
В предельном случае p=∞, положим .

Заметим, что  не является нормой при 1≤p<∞.

Действительно, ясно, что

Применяя неравенство , заключаем, что

Последнее означает, что представляет собой так называемое квазинормированное векторное пространство. (В отличие от нормированных пространств, где выполняются неравенство треугольника , в квазинормированных пространствах имеет место лишь "квази-неравенство треугольника"  для некоторого k≥1.) Однако, при p>1 в пространстве можно ввести норму, при наделении которой оно становится банаховым пространством.

Теорема 1.2 (Интерполяционная теорема Марцинкевича)

Пусть p0≠p1 и

T:  с нормой ,

T:  с нормой .

Положим ; , и допустим, что p≤q.

Тогда T: →, с нормой μ, удовлетворяющей неравенству .

Эта теорема, напоминает теорему Рисса-Торина, но отличается от нее во многих важных отношениях.

Во-первых, здесь скаляры могут быть как вещественными, так и комплексными, в то время как в теореме Рисса-Торина обязательно нужно, чтобы скаляры были комплексными. Во-вторых здесь имеется ограничение p≤q. Наиболее важная особенность состоит в том, что в предпосылках теоремы пространства  и  заменены на более широкие пространства  и .

Таким образом, теорема Марцинкевича может оказаться применимой в тех случаях, где теорема Рисса-Торина уже не работает.

2 . Общие свойства интерполяционных пространств

Пусть A - векторное пространство над полем вещественных или комплексных чисел. Оно называется нормированным векторных пространством, если существует вещественнозначная функция (норма) , определенная на A, удовлетворяющая условием.

1) , причем

2)  (λ-скаляр)

3) .

Пусть A и B – два нормированных векторных пространства. Отображение T из A в B называется ограниченным линейным оператором, если

,  и .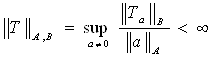

Ясно, что всякий ограниченный линейный оператор непрерывен.

Пусть A0 и A1 – топологических векторных пространства. Говорят, что

A0 и A1 совместимы, если существует отделимое топологическое векторное пространство U, такое, что A0 и A1, являются подпространствами. В этом случае можно образовать сумму A0 + A1, и пересечение A0∩A1. Сумма состоит из всех aU, представимых в виде a=a0+a1, где a0A, и a1A,

Справедлива следующая лемма

Лемма 2.1. Пусть A0 и A1-совместимые нормированные векторные пространства. Тогда

A0∩A1, есть нормированное векторное пространство с нормой

A0 + A1, также представляет собой нормированное векторное пространство с нормой

При этом если A0 и A1 – полные пространства, то A0∩A1 и A0 + A1 также полны.

Дадим некоторые важные определения:

Категория σ состоит из объектов A,B,C…., и морфизмов R,S,T,…. между объектами и морфизмами определено трехместное отношение T: A↷B.

Если T: A↷B и S: B↷C, то существует морфизм ST, называемый произведением (или композицией) морфизмов S и T, такой, что ST: A↷ C.

Операция взятия произведения морфизмов удовлетворяет закону ассоциативности: T(SR)=(TS)R. далее, для всякого объекта A из σ существует морфизм I=IA, такой, что для любого морфизма T: A↷A TI=IT=T

Через σ1 обозначим категорию всех совместимых пар  пространств из σ.

Определение 2.1. Пусть =(A0,A1)-заданная пара из σ1. Пространство A из σ будем называть промежуточным между A0 и A1 (или относительно ), если имеют место непрерывные вложения.

 .

Если, кроме, того T: ↷ влечет T: A ↷ A, то A называется интерполяционным пространством между A0 и A1.

Более общим образом, пусть и - две пары из σ1. Тогда два пространства A и B из σ называются интерполяционными относительно и соответственно и T: ↷ влечет T: A↷ B.

Если выполнено

,


В этом случае, говорят, что A и B равномерные интерполяционные пространства.

Определение 2.2 Интерполяционные пространства A и B называются пространствами типа θ (0≤θ≤1), если

В случае с=1 говорят, что A и B - точные интерполяционные пространства типа θ.

 

3. О норме и спектральном радиусе неотрицательных матриц

Хорошо известно, что проблема нахождения нормы линейного оператора, спектрального радиуса оператора являются трудной проблемой и в конечномерном случае. В то же время, иногда важно не вычисляя нормы оператора знать, как она изменится в случае некоторого преобразования.

В данной работе изучается влияние распределения ненулевых элементов неотрицательной матрицы на норму соответствующего оператора и спектрального радиуса.

Определим пространство  как множество всех наборов вида

a=(a1, a2,…, aN)

с нормой

.


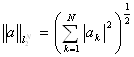Множество Q={(k,l):k,l=1,…,N} назовем решеткой размерности N x N. Любое множество Q0={(ki,lj): , } будет являться подрешеткой размерности r x m.

Спектральный радиус линейного оператора в конечномерном пространстве  определяется следующим образом:

r(A)=,

где lk- собственные значения оператора A.

Пусть m ≤ N, d1,…,dm - положительные числа. Через Dm обозначим множество неотрицательных матриц А, ненулевые элементы которых принимают значения d1,…,dm. Через P(A) обозначим множество индексов соответствующих положительным элементам. Пусть AÎDm. Если D={(ki,lj), i=1,…,q, j=1,…,p} подрешетка, содержащая P(A), то для соответствующего оператора А

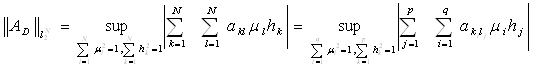
Как видно из этого определения, от перестановки строк и столбцов матрицы норма не меняется.

Пусть даны положительные числа d1,…,dm и натуральное число m < N2.

Будем исследовать следующие вопросы:

Как расположить числа d1,…,dm в решетке Q, чтобы норма линейного оператора AQ соответствующего решетке (матрице) Q была максимальной? 

Пусть в неотрицательной решетке Q m положительных элементов. Как расположить (m+1)-ый элемент, чтобы норма линейного оператора AQ соответствующей полученной решетке была максимальной?

Как расположить числа d1,…,dm в решетке Q, чтобы спектральный радиус был минимальным (максимальным)?

Справедливы следующие теоремы:

Теорема 3.1 Пусть d1,…,dm положительные числа, Dm - класс неотрицательных матриц, ненулевые элементы которых принимают значения d1,…,dm. Если m ≤ N, Q0 -произвольная подрешетка размерности 1 m, то

.

Доказательство. Воспользуемся определением и неравенством Коши-Буняковского, получаем

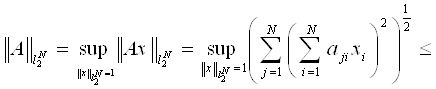
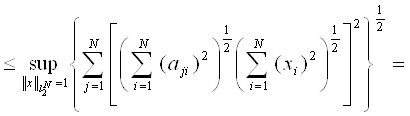
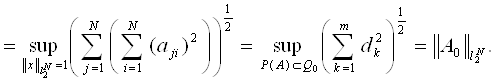
Неравенство в обратную сторону очевидно.

Теорема доказана.

Данное утверждение говорит о том, что если ненулевых элементов меньше либо равно N, то своего максимума норма достигается когда все ненулевые элементы расположены в одной строке или в одном столбце.

Теорема 3.2 Пусть d1=…=dm=d, то есть Dm – множество всех матриц, имеющие m ненулевых элементов, которые равны числу d. Q0 -произвольная решетка, симметричная относительно главной диагонали размерности nn, где n=min{r: r2 ≥ m}. Тогда

,

где [m1/2] - целая часть числа m1/2.

Доказательство. Из свойства спектрального радиуса имеем для AÎDm

.

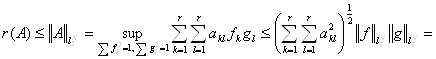
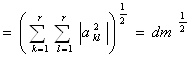Пусть Q1 -подрешетка, также симметричная относительно главной диагонали размерности . Тогда для AÎDm, Q1ÌP(A)ÌQ0 имеет место представление

А=А1+А0, где А1,А0ÎDm, Р(А1)=Q1, P(A0)ÌQ1\Q0.

Учитывая, что матрицы А0 и А1 неотрицательны, получаем

,

поэтому r(A0)≤r(A).

С другой стороны А1 – симметричная матрица и следовательно


.

Таким образом,

.

Теорема доказана.

Теорема 3.3 Пусть множество GÌQ, где Q - решетка размерности nn таково, что, если (k,l)ÎG, то (l,m),(n,k)ÏG для всех n,mÎ{1,2,…,N}.

Тогда, если P(A)ÌG, то r(P(A))=0.

Доказательство. Не трудно проверить, что для матрицы А с ненулевыми элементами из G (т.е. P(A)ÌG) имеет место равенство А2=0, т.е. А – нильпотентная матрица индекса 2 и следовательно у нее единственное собственное значение 0.

Теорема доказана.

Теорема 3.4 Пусть AÎDm. Пусть Q0 -минимальная подрешетка содержащая P(A), (Q0ÉP(A)) такая, что в каждой строке и в каждом столбце находится хотя бы один элемент соответствующий нулевому элементу матрицы A.

Пусть Ad – матрица, полученная из матрицы A добавлением элемента со значением d>0 в одно из свободных мест, тогда

Доказательство.

Так как норма оператора не зависит от перестановки строк и столбцов матрицы, то можно считать, что решетка A0={(i,j), i=1,…,l; j=1,…,m} расположена в левом верхнем углу матрицы A. Пусть курсовые - 700 р.


Назад