Учебное пособие: Численные методы
ЛЕКЦИЯ № 12
ТИПОВЫЕСПОСОБЫ ПРИБЛИЖЕНИЯ ПРИ ПОМОЩИ МНК НЕЛИНЕЙНЫХ ФУНКЦИЙ В ЛИНЕЙНЫЕ
Подавляющее большинство процессов реального мира носит линейный характер, поэтому область, использования линейных моделей весьма ограничена, в то же время для построения нелинейных моделей хорошо разработан математический аппарат. Рассмотрим некоторое преобразование, позволяющее при построении нелинейными функциями воспользоваться методом МНК для линейной функции.
Аппроксимируемая Линейная Замена
функция функция
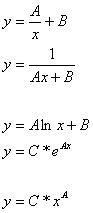
![]()
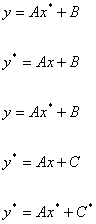
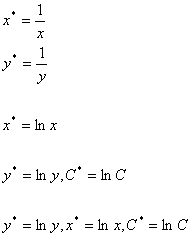
Вообще полиномы выше 6-ой степени при помощи МНК никогда не строят, т.к. появляются серьёзные ошибки округлений и раскачивания. На практике ограничиваются квадратической зависимостью.
МНК для системы линейно- независимых функций.
Пусть задана система
линейно-независимых функций одной переменной ![]() .
Под линейно-независимой функцией понимаем такую систему, в которой ни одна из
функций не может быть представлена в виде линейной комбинации остальных
функций.
.
Под линейно-независимой функцией понимаем такую систему, в которой ни одна из
функций не может быть представлена в виде линейной комбинации остальных
функций.
Задана f(x) таблично на [a;b] по системе узлов xj ,yj=f(xj)
Рассмотрим приближение f(x) при помощи обобщенного многочлена:
![]() (12.1)
(12.1)
Необходимо найти неизвестные коэффициенты из (12.1)
![]() (12.2)
(12.2)
Критерий (12.2) представляет собой квадратичную функцию относительно параметров bi.
Запишем
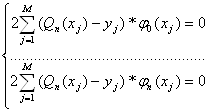 (12.3)
(12.3)
Получим
 (12.4)
(12.4)
Система (12.4) представляет собой СЛАУ относительно параметров bi и может быть решена одним из известных методов.
Рассмотрим
один из частных случаев этой системы, когда функции ![]() являются
ортогональными.
являются
ортогональными.
Введем понятие скалярного произведения функции.
![]() (12.5)
(12.5)
Линейно-независимая
система функций ![]() является
ортогональной если
является
ортогональной если
![]()
Для системы ортогональных функций решение системы (12.4) получается элементарно.
 (12.6)
(12.6)
Коэффициенты (12.6) называются коэффициентами Фурье, а многочлен (12.1) называется обобщенным многочленом Фурье.
Тригонометрические ряды и полиномы Фурье в использовании МНК
Для приближения тригонометрических функций в анализе используют тригонометрические ряды Фурье.
Периодической называется функция, для которой выполняется равенство:
f(x+KP)=f(x)
P-наименьший положительный период.
Пусть g(x) имеет P, тогда f(x)=g(Px/2π) будет иметь период 2π.
Пусть f(x) –функция, имеющая период 2π, тогда она может быть представлена рядом:
![]() (12.7)
(12.7)
 (12.8)
(12.8)
(12.8) тригонометрический ряд Фурье.
![]() (12.9)
(12.9)
Коэффициенты Фурье могут быть получены также методом МНК для системы ортогональных линейно-независимых функций.
Пусть значения таблично-заданной функции известны в точках
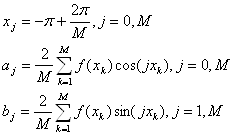
Тригонометрические полиномы используются для тригонометрических процессов.
ЛЕКЦИЯ №13
ЧИСЛЕННЫЕ ДИФФИРИНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
Численное дифференцирование
1.1 Расчет производных аналитически заданной функции
1.2 Нахождение производных таблично заданной функции
Численное интегрирование
2.1 Формулы прямоугольников
2.2 Формулы Ньютона - Котеса
Формулы Симпсона и Ньютона
2.3 Формулы Чебышева и Гаусса
Численное дифференцирование применяется в случаях, когда аналитическое нахождение производных приводит к громоздким вычислениям, (особенно при необходимости иметь одинаковый алгоритм для вычисления производных заданных функций, а также тогда, когда функция задана таблично).
§1.1 Для аналитически заданных функций рассмотрим следующие способы численного дифференцирования:
1.) предел отношения приращений;
2.) при помощи центрированных разностях;
Предел отношения приращений
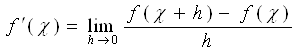
Строим последовательности {hk}так, чтобы hk→0 вычисляем предел последовательности {Dk}, где
Dk= 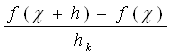 k=1,2..n
k=1,2..n
Вычисления проводят до некоторого n, при котором выполняется условие:
|Dn+1-Dn|≥|Dn-Dn-1|
Шаг выбираем сами (обосновать).
Центрированные разности
Пусть наша функция трижды непрерывно дифференцируема на [a;b]:
f![]() c3[a;b] x-h, h,
x
c3[a;b] x-h, h,
x![]() [a;b]
[a;b]
тогда 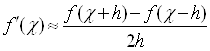
Эта приближенная формула имеет 2-ой порядок точности.
Ошибка: 0(h2). Разложим функцию в ряд Тейлора:
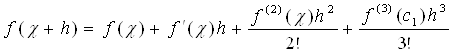
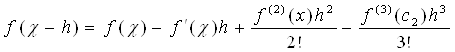
Вычтем из первого равенства второе:
f(x+h)-f(x-h)
ЛЕКЦИЯ №14
В случае, когда нельзя выразить , либо функция задана таблично , нахождение интеграла по формуле Ньютона-Лейбница невозможно.
Используют приближенные формулы, которые называют квадратурными, либо формулами численного интегрирования.
1) Формулы прямоугольника
Пусть y=f(x) непрерывна на [a,b].
Требуется вычислить  .
.
Разобьем отрезок интегрирования на n равных частей, точками xi, i=0,n

xi=a-i*h
![]() шаг разбиения
шаг разбиения
На отрезке [xi-1;xi] возьмем произвольную точку xi . Из определения наш интеграл равен 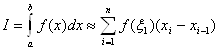 (14.1)
(14.1)
общая форма прямоугольника.
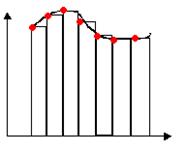 Геометрическая
интерпритация формулы прямоугольника.
Геометрическая
интерпритация формулы прямоугольника.
Площадь ограничена графиком функции y=f(x) на отрезке осью абцис и заменяется площадью прямоугольника с высотой равной f(xi). Отметим частный случай формулы прямоугольника.
1)
Пусть xi это xi. Из формулы 14.1 видно ![]() .
.
Точность 0(h) порядка один. Формула левых прямоугольников
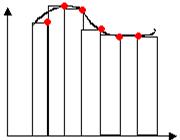 2) xi=xi.
2) xi=xi. ![]() формула
правых прямоугольников 0(h).
формула
правых прямоугольников 0(h).
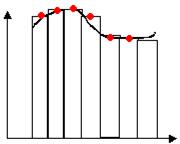
3) xi=1/2 (xi-1+ xi). Получилась формула средних
прямоугольников. ![]() . Точность
порядка два 0(h2).
. Точность
порядка два 0(h2).
2)Формула Ньютона-Котеса
 -общая формула
-общая формула
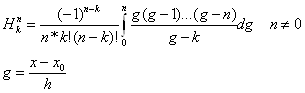
Н-коэффициент Котеса.
xk=a+b*h k=0,n
Пусть n=1 значит ![]()
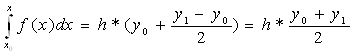
Пусть n=2 значит ![]()
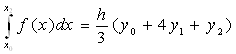
Применение формулы Ньютона-Котеса высоких порядков может быть оправдана при достаточно высокой гладкости подинтегральной функции, поэтому промежуток интегрирования будем дробить на мелкие части, на каждой из которых можно применить формулу Н-К невысокого порядка. Выведем формулу трапеции Симсона-Ньютона.
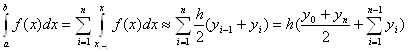
 yi=f(xi), i=0,n. Точность порядка два 0(h2). Эта формула точна для многочленов первой степени.
yi=f(xi), i=0,n. Точность порядка два 0(h2). Эта формула точна для многочленов первой степени.
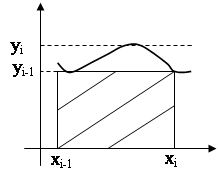
Геометрическая интерпритация
На элементарном отрезке [xi-1;xi] площадь под кривой полагают равной площади трапеции с основаниями yi-1 и yi и высотой h. h= xi-xi-1
Формула Симсона
 Пусть n=2m. Число разбиения отрезков четное. Тогда
Пусть n=2m. Число разбиения отрезков четное. Тогда 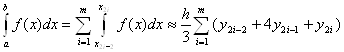 точна для многочлена в
третьей степени.
точна для многочлена в
третьей степени.
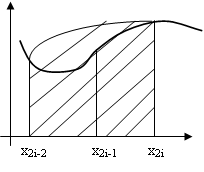
Геометрическая интерпритация
На отрезке [x2i-2;x2i] длиной 2h
Cтроится парабола, проходящая через три точки. Площадь под параболой, заключення между осью абцисс и прямыми x2i-2 и x2i и принимает равный интеграл.
Формула Ньютона – это формула Симсона 3/8.
Пусть n=3m. Количество отрезков разбиения нечетное.
 точна для полиномов третьей степени.
точна для полиномов третьей степени.
2) Формула Чебышева- Гаусса
Квадратуры Гаусса используют, если интегрируемая функция задана
аналитически. Подинтегральную функцию апроксимируют полиномами различных
степеней. Общий вид линейно-квадративной формулы 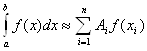 , где Ai-
весовые функции.
, где Ai-
весовые функции.
Формула Гаусса: ![]() точна
для многочленов N=2n-1 степени.
Ai и ti вычислены и
табулированы
точна
для многочленов N=2n-1 степени.
Ai и ti вычислены и
табулированы
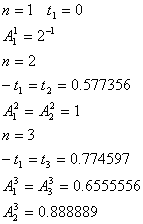
Формула Чебышева:![]() точна
для многочлена степени n.
точна
для многочлена степени n.
Точки ti вычислены и табулированы для n=2,3…7,9. Для n=8 и больше 10 ti не сушествуют.
n=2 -ti=t2=0.577350
n=3 -ti=t3=0.707107 t2=0
n=4 -ti=t4=0.794654 -t2=t3=0.187592
Для вычисления интеграла по формулам 4 и 5 следует сделать замену
переменных ![]()
Тогда наш интеграл равен ![]()
Замечание: правило Рунге используется для оценки погрешности.
Вычисляют интеграл по выбранной квадративной формуледважды, сначала с шагом h, затем h/2. Затем ,если полученное значение >e, то полагают, что наш интеграл равен I=I2n ,иначе шаг h/4.
|In-I2n|<e
ЛЕКЦИЯ № 16
МЕТОД РУНГЕ-КУТТА (четвертого порядка)
Пусть поставлена задача Коши, где функция f(x,y) 4 раза непрерывно дифференцируема. Необходимо найти решение этой задачи на [x0,b], xk=x0+k*h, k=0,n; h=(b-x0)/n.
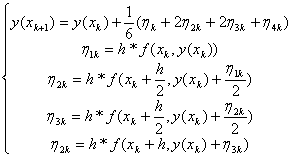 (16.1)
(16.1)
Многошаговые методы. Метод прогноза и коррекции Адамса.
Идея многошаговых методов заключается в том, что при расчете значения искомой функции к некоторой последующей точке xk+1 используют значение функции в нескольких предыдущих точках xk-1 , xk-2….общая точность метода равна количеству испытаний точек. Все m –шаговые методы можно описать формулами:
![]() 16.2
16.2
При b0=0 мы получаем явные методы, при b¹0 – неявные методы.
Обьединение идей явных и неявных методов, позволило получить методы прогноза и коррекции. Их суть в том, что на " шаге может быть получено значение отношения приближенного значения. у(х) от точного, и при необходимости, приближенное значение может быть исправлено, откорректировано на эту ошибку.
у(х0)-определяется из условия задачи Коши
у(х1),у(х2),у(х3)…у(хm-1) находится при помощи явных методов Рунге-Кутта. Многошаговые методы удобно применять на длинных отрезках [x0,b].
Рассмотрим методы погноза и коррекции Адамса 4 порядка.
Пусть поставлена задача Коши 15.3 необходимо найти значение у(х) на [x0,b] в т.xk
[x0,b] xk=x0+k*h k=0,n; h=(b-x0)/n
 16.3
16.3
Локальная точность
Известно, что на " шаге точное значение функции в т.хк у̃(хк) отличается от приближенного значения хк на величину.
![]() 16.4
16.4
![]() 16.5
16.5
![]() где ε заданная точность
где ε заданная точность
Решение задачи Коши для систем дифференциальных уравнений
Наиболее и лучше всего иследована система дифференциальных уравнений
1-го порядка. Система из n уравнений имеет вид:
 16.6
16.6
В векторном виде система 16.6 записывается так:
![]()
Начальные условия системы 16.6 имеют вид:
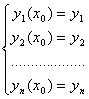 16.7
16.7
В общем виде система 16.6 имеет множество решений, а с начальным условием может иметь единственное решение.
Задачей Коши для системы из n дифференциальных уравнений 1-го порядка называются 16.6 с начальным условием 16.7.
Пример:
Пусть есть некоторый продукт. Известна скорость выпуска этого продукта (производительность). Необходимо составить модель, позволяющую прогнозировать колво продукции и общие затраты предприятия на ее изготовление и хранение. Пусть V-объем.
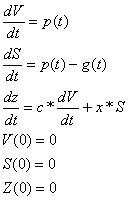
Метод Эйлера. Решение задач Коши для систем дифференциальных уравнений.
Пусть поставлена задача 16.6,16.7.
Необходимо найти значение функций у1…уn на отрезке [x0,b], xk=x0+k*h, k=0,m
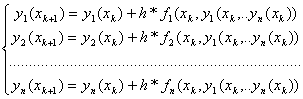 16.8
16.8
В векторном виде :![]()
Локальная точность порядка h2
Общая точность порядка h.
Метод Рунге-Кутта решения задач Коши для систем дифференциальных уравнений.
Пусть поставлена задача Коши 16.6,16.7. Необходимо найти значение функции на отрезке [x0,b] в т.хк…..
С этой целью исползуется рекурентная формула
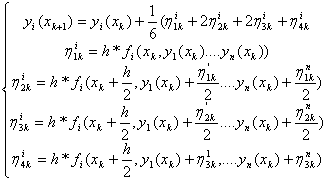 16.9
16.9
Решение дифференциальных уравнений высших порядков.
y(n) = f(x,y,y’,…y(n-1) 16.10
Для уравнения 16.10 можно задать следующее начальное условие:
 16.11
16.11
Решение 16.10 и 16.11 осуществляется путем перехода к эквивалентной задачи Коши для систем дифференциальных уравнений 1-го порядка.
Замена имеет вид:
z1 (x)=y’(x)
z2 (x)=y’’(x)
zn-1 (x)=y(n-1)(x)