Контрольная работа: Сходимость рядов

КОНТРОЛЬНАЯ РАБОТА № 9

ВАРИАНТ 9.3.

Найти область сходимости указанных рядов

9.3.1.

а)

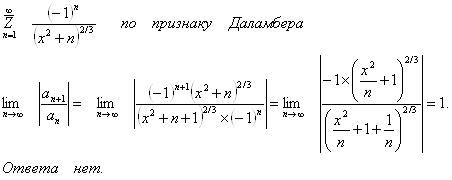
По признаку Лейбница для знакопеременных рядов  ряд сходится условно (соответствующий ряд Дирихле расходиться)

.

б)

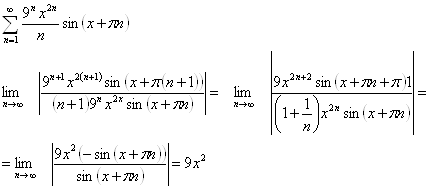
Отсюда следует, что при  ряд сходится, т.е. при . При  ряд расходится.

Рассмотрим случай

Для данного ряда выполняется теорема Лейбница для знакопеременных рядов  Ряд сходится условно, т.к. ряд

При  аналогично получим ряд , ряд сходится условно.

Ответ:

9.3.2.

а)

. По признаку Даламбера ряд сходится, если .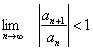

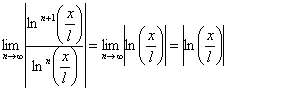
Ряд будет сходится при

Первый случай  или

В промежутке  ряд сходится.

Второй случай

В промежутке 1<x<l ряд сходится. Объединяем интервалы и получим . Рассмотрим концы интервала.

При x=1 получим ряд , т.е. ряд вида — -1+1-1+1-1+…

Данный ряд расходится, т.к. его сумма имеет два различных предела (колеблющийся ряд).

При  получим ряд  т.е. ряд вида 1+1+1+…; ряд расходится, т.к.

б)

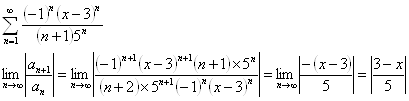
Ряд будет сходиться при .

1)

в интервале  ряд сходится.

2)

в интервале 3<x<8 ряд сходится.

Общий интервал сходимости –2<x<8.

На концах интервала х=-2, имеем ряд:

— расходящийся гармонический ряд.

в п.9.3.1 б) показано, что ряд сходится условно.

Ответ: (-2,8]

9.3.3.

а)

Ряд сходится при условии

1)

Решим неравенство:

корней нет, следовательно:  — всегда.

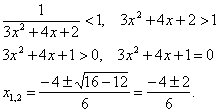
Ветви параболы направлены вверх, получаем два интервала:  Здесь ряд сходится.

Исследуем концы интервалов:

1) . Получаем ряд: 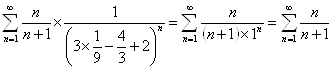. Ряд расходится, т.к. все его члены не меньше расходящегося гармонического ряда .

2)

б)

.

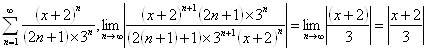Ряд сходится при .

1)  интервал сходимости .

2)  интервал сходимости .

Исследуем границы интервала.

1)

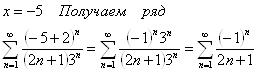
По теореме Лейбница ряд сходится, причем условно, т.к. ряд  — расходится.

2) .

Сравним с рядом  по второму признаку сравнения

расходится, то расходится и ряд .

3.9.4.

а)

Ряд сходится при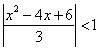

1)  тогда

корней нет, .

Решаем неравенство:

.

Решаем полученное неравенство:

В промежутке (1,3) ряд сходится.

На концах интервала имеем:

1)

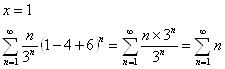
Ряд расходится, т.к. .

2)

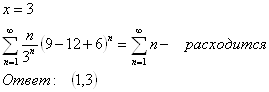
б)

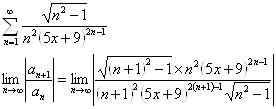
Ряд сходится при услови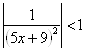и  или

Интервал сходимости .

На концах интервала.

1)

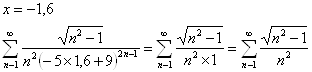
— ряд расходится, т.к. расходится ряд .

2)

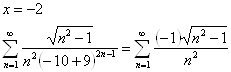
Ряд, как предыдущий, но все члены отрицательны.

9.3.5.

а)

Ряд сходится при условии .

1)

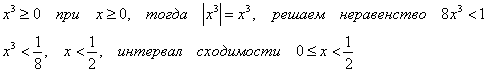
2)

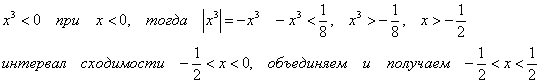
Исследуем концы интервала:

1)

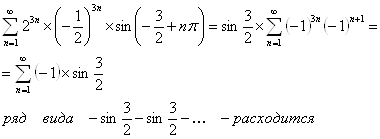
2)

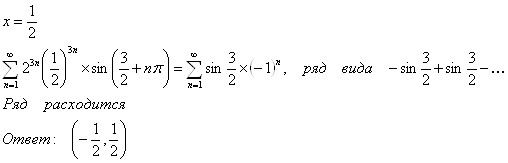
б)

Ряд сходится при условии  откуда

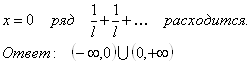
9.3.6.

а)

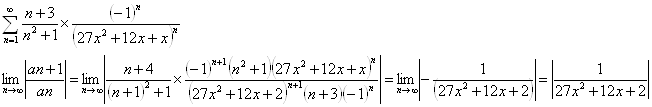
Ряд сходится при

и корней нет, следовательно, имеет условие

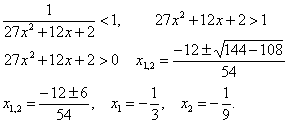
Интервал сходимости .

Исследуем концы интервалов:

1)

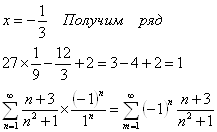
Ряд знакочередующийся, проверим условие Лейбница

 — выполняется

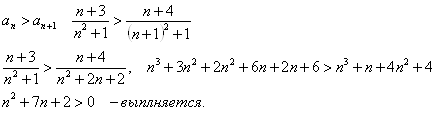
Ряд сходится при

Получим такой же ряд.

б)

Проверяем признак Даламбера:

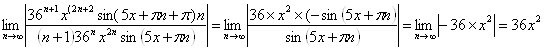
Условие сходимости

На концах интервала имеем:

1)

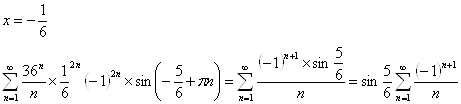
Ряд знакочередующийся, признак Лейбница выполняется.

Ряд сходится условно при .

Получим такой же ряд, но члены имеют обратные знаки.

.

9.3.7.

а)

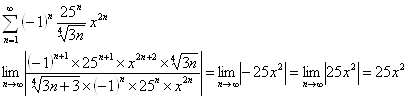
Проверяем концы интервалов

1)

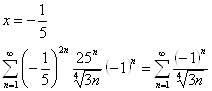
Признак Лейбница выполняется, ряд сходится.

При  получится такой же ряд (т.к. x в четной степени).

б)

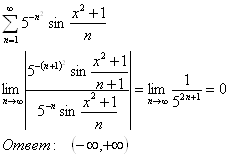
9.3.8.

а)

Условие сходимости .

Найдем дискриминант знаменателя: D=64-72<0. Условие принимает вид

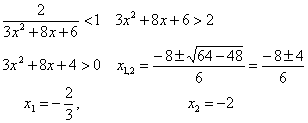
Интервал сходимости .

На концах интервала

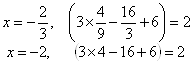
Получаем один и тот же ряд

.

Члены этого ряда не меньше членов ряда , следовательно, ряд расходится.

б)

Условие сходимости

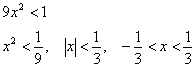
На краях интервалов:

1) . Получается ряд:

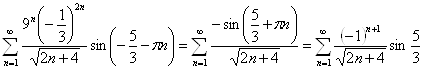
Ряд знакочередующийся, по признаку Лейбница сходится.

2)

9.3.9.

а)

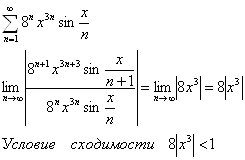
1. Если , т.е.  и необходимо решить неравенство: . Получается интервал .

2.

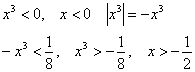
Интервал с учетом .

На концах интервала:

1)

Ряд сходится. Аналогично при .

.

б)

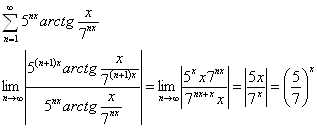
Интервал сходимости определяется неравенством

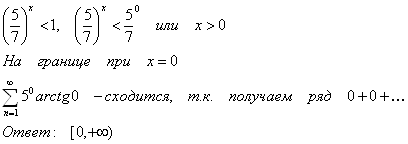
9.3.10.

а)

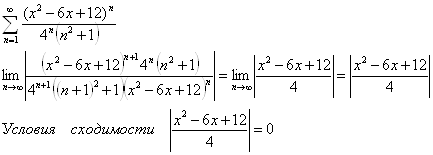
Найдем дискриминант числителя

б)

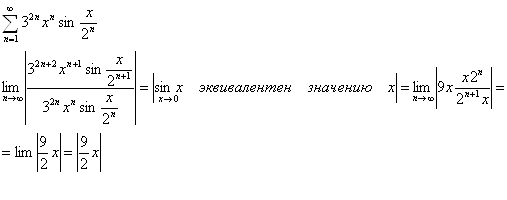
1)

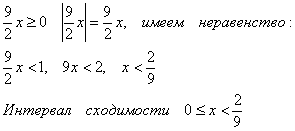
2)

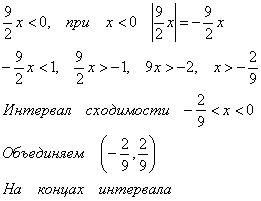
1.

2.