Курсовая работа: Проектирование привода технологического оборудования
КУРСОВАЯ РАБОТА
"Проектирование привода технологического оборудования"
Задание
1. Выполнить необходимые расчеты, выбрать наилучшие параметры схемы.
2. Разработать конструкторскую документацию:
– чертеж общего вида редуктора;
– чертеж разреза редуктора;
– чертеж корпусной детали;
– рабочие чертежи деталей: чертеж тихоходного вала, чертеж зубчатого колеса, чертеж крышки подшипникового колеса
| Тип ременной передачи | Частота вращения ведомого вала | Тип ременной передачи | Тип цепи | Режимы работы |
Ревер- сивность |
Продолжи- тельность включений% |
Срок Службы в годах |
Коэффициент использования привода | |
| 5 | 55 | плоско ременная | ПР | Легкий | Н/Р | 20 | 8 | В течении года | В течении суток |
| 0,7 | 0,6 |
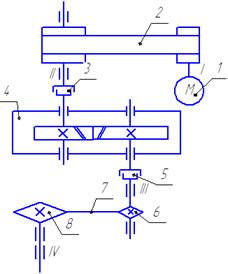
Рисунок 1 – Кинематическая схема привода
Введение
Объектом изучения расчетов и проектирования является привод технологического оборудования состоящий из двигателя, ременной передачи и двухступенчатого цилиндрического редуктора. Зубчатые редукторы подобного типа широко используются в приводе различных машин (транспортеры, металлорежущие станки и т.д.). Рассматриваемый привод служит для передачи крутящего момента на исполнительный орган – транспортер.
Для проектирования редуктора выполнены проектные и проверочные расчеты зубчатых передач. Спроектированы (ременные / цепные) передачи.
На основе эскизного проектирования полученные данные для прочностных расчетов валов и подшипников качения. Расчеты выполненные на основании современных подходов по проектированию зубчатых передач с использованием критерия работоспособности – прочности по контактным напряжениям. На основе методики расчета по ГОСТ ………. Полученные размеры принимаются стандартными по ГОСТ…………….
Конструкторская часть проекта выполнена с применением системы автоматизированного проектирования «Компас» и «Autocad».
Пояснительная записка состоит из 25-ти страниц, рисунков 2, список литературы 15 наименований.
1. Выбор электродвигателя
1.1 Расчет требуемой мощности
Требуемая мощность электродвигателя, кВт
P1 = ![]() ,
,
где Рвых – выходная мощность на IV валу,
Рвых=5кВт;
η0 – общий КПД привода,
η0 = η1*η2 *η3*η4;
здесь ![]() – КПД одной пары
подшипников качения,
– КПД одной пары
подшипников качения, ![]() - КПД
ременной передачи, η3 – КПД цилиндрической передачи, η4 – КПД цепной
передачи примем
- КПД
ременной передачи, η3 – КПД цилиндрической передачи, η4 – КПД цепной
передачи примем ![]() = 0,99,
= 0,99, ![]() = 0.96,
= 0.96, ![]() 0,98, η4=0,97
0,98, η4=0,97
η0 =0,99*0,96*0,98*0,97=0,85
Тогда P1= ![]() =5,9 кВт
=5,9 кВт
По требуемой мощности из табл. П. 1 [1] выбираем асинхронный электродвигатель 132S6 с ближайшей большей стандартной мощностью Pэ = 5,5 кВт, синхронной частотой вращения nс = 1000 мин-1 и скольжением S = 3,3%.
Частота вращения вала электродвигателя
n1= nс (1 – ![]() ) = 1000
) = 1000![]()
![]() мин
мин![]()
Общее передаточное число привода
uo=![]() =
=![]()
Передаточное число зубчатой передачи
u’= ![]() =
=![]() = 2,93
= 2,93
Округлим u’ до ближайшего стандартного значения (табл. 3 [1]). Принимаем u= 3,15
1.2 Частоты вращения валов
Частоты вращения валов (индекс соответствует номеру вала на схеме привода):
n1= 967 об/мин
n2= 483,5 об/мин
n3= 153,5 об/мин
n4= 51,2 об/мин
1.3 Мощность на валах
Мощности, передаваемые валами:
P1 = Р![]() = 5,9 кВт
= 5,9 кВт
P2 = Р![]()
![]() = 5,61 кВт
= 5,61 кВт
P3= Р![]()
![]() =
5,33 кВт
=
5,33 кВт
P4= Р![]()
![]() = 5,33 кВт
= 5,33 кВт
1.4 Крутящие моменты, передаваемые валами
Крутящие моменты, передаваемые валами, определяется по формуле
Ti = 9550![]() .
.
Тогда T1= 58,3 Нм
T2= 110,8 Нм
T3= 331,6 Нм
T4= 955 Нм
Полученные данные заносим в таблицу П2;
Таблица 2
|
№ вала |
Ni об/мин |
Pi кВт |
Ti Нм |
| 1 | 967 | 5.9 | 58 |
| 2 | 483.5 | 5.61 | 111 |
| 3 | 153.5 | 5.33 | 332 |
| 4 | 51.2 | 5.12 | 955 |
2. Расчет цилиндрической прямозубой передачи
2.1 Выбор материалов
Исходные данные:
Тип зуба – Косой. Тип передачи – нереверсивная.
Крутящий момент на шестерне Т2 = 111 Н•м
Частота вращения шестерни n2= 483,5 мин-1
Передаточное число u= 3,15
Режим нагружения – легкий
Коэффициент использования передачи:
в течение года – Kг = 0,7
в течение суток – Kс = 0,6
Cрок службы передачи в годах – L = 8
Продолжительность включения – ПВ = 20%
Для выбора материала определим размеры характерных сечений заготовок по формулам:
Dm=20*![]() =20*
=20*![]() =65.6 мм
=65.6 мм
Sm=1.2*(1+U)*![]() = 1.2*(1+3.15) *
= 1.2*(1+3.15) *![]() =16.33 мм
=16.33 мм
Материалы выбираем по табл. 4 [1]
При выборе материала заготовок должны выполняться следующие условия:
Dm= Dm1; Sm= Sm1.
Шестерня:
Материал – Сталь 45
Термическая обработка – Улучшение
Твердость поверхности зуба – 269–302 HB
Колесо:
Материал – Сталь 45
Термическая обработка – Улучшение
Твердость поверхности зуба – 235–262 HB
Средние значение твердости поверхности зуба и колеса:
HB1=0.5*(HB1min+HB1max)=0.5*(269+302)=285.5
HB2=0.5*(HB2min+HB2max)=0.5*(235+262)=248.5
2.2 Допускаемые контактные напряжения
![]() HPj =
HPj =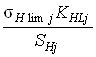
где j=1 для шестерни, j=2 для колеса;
sHlim j - предел контактной выносливости (табл. 5 [1]),
sHlim1 = 2HB1+70=641 МПа
sHlim2 = 2HB2+70=567 МПа
SHj - коэффициент безопасности (табл. 5 [1]),
SH1= 1,1 SH2= 1,1
KHLj - коэффициент долговечности;
KHLj =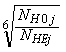
![]() 1,
1,
здесь NH0j – базовое число циклов при действии контактных напряжений (табл. 4 [1]),
NH01= 23,5*10![]() NH02 = 16.8*10
NH02 = 16.8*10![]()
![]()
Коэффициент эквивалентности при действии контактных
напряжений определим по табл. 6 [1] в зависимости от режима нагружения: ![]() h =
0,125
h =
0,125
Суммарное время работы передачи в часах
th = 365L24KгКсПВ = 365*8*24*0,7*0,6*20 = 5887 ч
Суммарное число циклов нагружения
NSj = 60 nj c th, NS2=![]()
где с – число зацеплений колеса за один оборот, с = 1;
nj – частота вращения j-го колеса, n2= 483,5 мин-1
NS1=![]() 1,71
1,71![]()
![]() ;
NS2=
;
NS2=![]() =0,54
=0,54![]()
![]()
Эквивалентное число циклов контактных напряжений, NHE j= ![]() h NΣj;
h NΣj;
NHE1=0,21![]()
![]()
![]() NHE2=0,07
NHE2=0,07![]()
![]()
Коэффициенты долговечности
KHL1= 1,02 KHL2= 1,16
Допускаемые контактные напряжения для шестерни и колеса
sHP1=![]() =594,38 МПа sHP2
=594,38 МПа sHP2![]() = 597,93 МПа
= 597,93 МПа
Для прямозубых передач sHP=sHP2, для косозубых и шевронных передач
sHP=0.45
(sHP1+sHP2)=0,45*(594,38+597,93)=536,54 МПа![]() sHPI
sHPI
sHPI=1.23*sHP1=731.1 МПа
Допускаемые контактные напряжения передачи:
sHP= 536.54 Мпа
2.3 Допускаемые напряжения изгиба
![]() FPj=
FPj=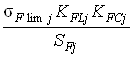 ,
,
где sF lim j - предел выносливости зубьев при изгибе (табл. 7 [1]), sF limi=1.75*HBi
sF lim 1 = 499,6 МПа sF lim 2 = 434,9 Мпа
SFj - коэффициент безопасности при изгибе (табл. 7 [1]), SF1= 1,7, SF2= 1,7;
KFCj - коэффициент, учитывающий влияние двухстороннего приложения нагрузки, (табл. 7 [1]) KFC1= 0,65, KFC2= 0,65
KFLj - коэффициент долговечности при изгибе:
KFL j=
![]() 1.
1.
здесь qj – показатели степени кривой усталости: q1 = 6, q2 = 6 (табл. 6 [1]);
NF0 – базовое число циклов при изгибе; NF0 = 4•106.
NFEj –
эквивалентное число циклов напряжений при изгибе; NFE j= ![]() Fj NΣj.
Fj NΣj.
Коэффициент эквивалентности при действии напряжений изгиба определяется по табл. 6 [1] в зависимости от режима нагружения и способа термообработки:
![]() F1 =0.038,
F1 =0.038, ![]() F2 =0.038,
F2 =0.038,
NFE1 =![]() =6,5
=6,5![]() , NFE2 =
, NFE2 =![]() =2,1
=2,1![]()
KFL1 =![]() , KFL2 =
, KFL2 =![]()
Допускаемые напряжения изгиба:
![]() FP1=
FP1= ![]() 191,03
МПа
191,03
МПа
![]() FP2=
FP2= ![]() 282,67
МПа
282,67
МПа
2.4 Геометрические параметры передачи
Межосевое расстояние определяем из условия контактной прочности:
![]() =
=![]() (u + 1)
(u + 1)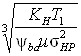 ,
,
где ![]() –
коэффициент вида передачи,
–
коэффициент вида передачи, ![]() =
410
=
410
KН – коэффициент контактной нагрузки, предварительно примем KН =1.2.
Коэффициент ширины зубчатого венца ![]() = 0,4 (ряд на с. 4
[1]).
= 0,4 (ряд на с. 4
[1]).
Расчетное межосевое расстояние ![]() =
121,84 мм
=
121,84 мм
Округлим ![]() до
ближайшего большего стандартного значения (табл. 2 [1])
до
ближайшего большего стандартного значения (табл. 2 [1])
![]() =
125 мм.
=
125 мм.
Модуль выберем из диапазона (для непрямозубых передач стандартизован нормальный модуль mn)
mn = ![]() =(0,01…0,02)
125=(1,25…2,5)
=(0,01…0,02)
125=(1,25…2,5)
Округлим mn до стандартного значения (табл. 1 [1]): mn = 2
Суммарное число зубьев:
Z![]() =
=![]() ,
,
где ![]() =
=![]() для прямозубых передач,
для прямозубых передач, ![]() =
=![]() для косозубых передач и
для косозубых передач и ![]() =
=![]() для шевронных передач.
для шевронных передач.
Z![]() =
=
![]() 122,27
122,27
Значение Z![]() округлим до ближайшего целого числа Z
округлим до ближайшего целого числа Z![]() =123
=123
Уточним для косозубых и шевронных передач делительный угол наклона зуба:
![]() =
arccos
=
arccos 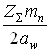 =
=![]()
![]()
Число зубьев шестерни:
Z1=![]() =
=![]() =29,6
=29,6
Округлим до ближайшего значения Z1=30
Число зубьев колеса:
Z2= Z![]() –
Z1=123–30=93
–
Z1=123–30=93
Фактическое передаточное число:
uф = ![]() =
=![]() =3,1
=3,1
Значение uф не должно отличаться от
номинального более чем на 2.5% при u![]() 4.5
и более чем на 4% при u > 4.5.
4.5
и более чем на 4% при u > 4.5.
![]() u = 100
u = 100  =100
=100![]()
Поскольку Z1>17 примем коэффициенты смещения: x1= 0, x2= 0
Ширинa венца колеса:
bw2=![]()
![]() =0,4
=0,4![]() 50
50
Округлим bw2 до ближайшего числа из ряда на с. 10 [1].
Ширину венца шестерни bw1 примем на 3 мм больше чем bw2:
bw1= 50+3=53
Определим диаметры окружностей зубчатых колес, принимая далее для непрямозубых колес m = mn.
Диаметры делительных окружностей прямозубых колес dj = mZj,
то же, для косозубых колес 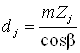 :
:
d1 =![]() =61 мм; d2 =
=61 мм; d2 =![]() =188 мм.
=188 мм.
Диаметры окружностей вершин при x![]() = 0: daj = dj + 2m (1 + xj):
= 0: daj = dj + 2m (1 + xj):
da1 =![]() 65 мм; da2=
65 мм; da2=![]() 192 мм
192 мм
Диаметры окружностей впадин dfj = dj – 2m (1.25 – xj):
df1 =![]() 56 мм; df2 =
56 мм; df2 =![]() 183 мм
183 мм
Вычислим окружную скорость в зацеплении
V =![]() =
=![]() 1,54 м/с
1,54 м/с
Степень точности передачи выбираем по табл. 8 [1] в зависимости от окружной скорости в зацеплении: nст=8
2.5 Проверочные расчеты передачи
2.5.1 Проверка прочности на выносливость по контактным напряжениям
Условие контактной прочности передачи имеет вид ![]()
![]()
![]() .
.
Контактные напряжения равны
![]() =
=![]()
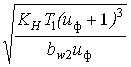 ,
,
где
Z![]() - коэффициент вида
передачи, Z
- коэффициент вида
передачи, Z![]() = 8400
= 8400
KН – коэффициент контактной нагрузки,
KН = KHα KHβ KНV.
Коэффициент неравномерности распределения нагрузки между зубьями
KHα =1+ A (nст – 5) Kw=1+0,15 (8–5)*0,228=1,103
где А = 0.06 для прямозубых и А = 0.15 для косозубых и шевронных передач;
Kw – коэффициент, учитывающий приработку зубьев.
Kw = 0.002НВ2 +
0.036 (V – 9)=![]() 0,228
0,228
Коэффициент неравномерности распределения нагрузки по ширине колеса
KHβ =1+ (K![]() – 1) Kw,
– 1) Kw,
где K![]() – коэффициент распределения нагрузки в начальный период
работы, определяемый по табл. 9 [1] в зависимости от коэффициента ширины венца
по диаметру.
– коэффициент распределения нагрузки в начальный период
работы, определяемый по табл. 9 [1] в зависимости от коэффициента ширины венца
по диаметру.
![]() = 0.5
= 0.5![]() (u + 1)=
(u + 1)=![]() 0,83
0,83
K![]() =
1,07 KHβ
=1+(1,07–1)*0,228=1,02
=
1,07 KHβ
=1+(1,07–1)*0,228=1,02
Динамический коэффициент определим по табл. 10 [1]
KНV= 1,06
Окончательно получим
KH=![]() 1,193
1,193
Расчетные контактные напряжения
![]() =
=![]() 515,657МПа
515,657МПа
Допускается перегрузка по контактным напряжениям не более 5%, рекомендуемая недогрузка до 15%. Расчет перегрузки или недогрузки выполним по формуле
![]()
![]() =100
=100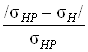 =
=![]() =3,9%
=3,9%
2.5.2 Проверка на прочность по напряжениям изгиба
Условия изгибной прочности передачи имеют вид sFj![]() sFPj.
sFPj.
Напряжение изгиба в зубьях шестерни
![]()
![]() sFP1,
sFP1,
где YFj - коэффициенты формы зуба;
KF - коэффициент нагрузки при изгибе;
Yb - коэффициент, учитывающий влияние угла наклона зуба на его прочность: Yе= коэффициент, учитывающий перекрытие зубьев.
Напряжение изгиба в зубьях колеса

![]() sFP2.
sFP2.
Коэффициенты формы зуба
YFj=3.47 + ![]() ,
,
где ZVj – эквивалентное число зубьев, для непрямозубых передач ZVj = 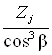 .
.
ZV1 = ![]() =31,48;
ZV1 =
=31,48;
ZV1 = ![]() =97,586
=97,586
YFj=3.47 + ![]() =3,89 YFj=3.47 +
=3,89 YFj=3.47 + ![]() =3,61
=3,61
Коэффициент, учитывающий влияние угла наклона зуба на его прочность:
Yb=![]()
Коэффициент, учитывающий перекрытие зубьев:
![]() ;
;
где ![]() коэффициент
торцевого перекрытия:
коэффициент
торцевого перекрытия:
![]()
Коэффициент нагрузки при изгибе
KF = KFα KFβ KFV=![]()
Коэффициент неравномерности распределения нагрузки между зубьями
KFα =1+0,15 (ncт-5)=1–0,15 (8–5)=1,45
Коэффициент неравномерности распределения нагрузки по ширине колеса
KFβ = 0.18 + 0.82K![]() =
=![]() 1,057
1,057
Динамический коэффициент при НВ2 < 350
KFV = 1+
1.5 (KHV –
1)=![]() 1,09
1,09
Напряжения изгиба
sF1=![]() =117.11 МПа
=117.11 МПа
sF2=![]() =133.76 МПа
=133.76 МПа
Допускается перегрузка по напряжениям изгиба не более 5%, недогрузка не регламентируется.
Условия изгибной прочности передачи выполняются, поскольку sF1![]() sFP1 и sF2
sFP1 и sF2![]() sFP2.
sFP2.
2.6 Силы в цилиндрической косозубой передаче.
Окружная сила
Ft = 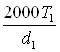 =
=![]() = 3639 Н
= 3639 Н
Распорная
сила Fr = Ft ![]() =
=![]() = 1346 Н
= 1346 Н
Осевая сила Fа = Ft*tg![]() =3639*
=3639*![]() =659 H
=659 H
3. Расчет валов
3.1 Проектный расчет и конструирование быстроходного вала.
Расчет выполняется
на кручение по пониженным допускаемым напряжениям [![]() k]=20 МПа. Ориентировочно
определим диаметр вала в опасном сечении, мм
k]=20 МПа. Ориентировочно
определим диаметр вала в опасном сечении, мм
d=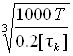 =
=![]()
где Т – крутящий момент в опасном сечении вала, T= 332 Н×м
Полученное значение округлим до ближайшего числа из ряда на с. 5 [2]: d= 45,
Длина ступицы будет равна:
![]()
Диаметр ступицы определим по формуле:
![]()
Тогда расстояние от середины ширины зубчатого колеса до середины ширины подшипника будет:
А=12+5+10+27=54 мм
1. Определение опорных реакций
Плоскость ZOX
Примем что
![]() ; Rвz=
; Rвz=![]()
![]() ; Rаz=
; Rаz=![]()
![]() ; Rвz + Rаz-Fr=1246+100–1346=0
; Rвz + Rаz-Fr=1246+100–1346=0
Плоскость XOY
![]() ; Rвy=
; Rвy=![]()
Ray= Ft – Rвy=3639–1819.5=1819.5Н=1,819 кН
2. Определение радиальных опорных реакций:
Rа =![]() =
= ![]()
RВ =![]() =
= ![]()
4. Расчеты подшипников качения
4. Расчет подшипников качения тихоходного вала. Шарикоподшипники радиальные однорядные легкой серии
Исходные данные
Расчет подшипника выполняем для наиболее нагруженной опоры.
Подшипник №46308
Размеры подшипника: d =40 мм, D = 90 мм, B = 23 мм
Динамическая грузоподъёмность C = 50,8 кН
Статическая грузоподъёмность C0 = 30,1 кН
Радиальная нагрузка на подшипник Fr = 1,346 кН
Осевая нагрузка на подшипник Fa = 0,659 кН
Частота вращения кольца подшипника n = 332 мин-1
Радиальные опорные реакции Ra=1.82 кН; Rв=2,21 кН.
Расчет подшипников на долговечность
1. Эквивалентная динамическая нагрузка
P = Kб KТ (XVFr + YFa),
где X – коэффициент радиальной нагрузки;
Y – коэффициент осевой нагрузки;
Kб - коэффициент безопасности (табл. 9 [2]); Kб=1,5
KТ – температурный коэффициент, KТ=1 при температуре подшипникового узла T <105![]() ;
;
V – коэффициент вращения, V=1 при вращении внутреннего кольца подшипника.
2. Параметры осевого нагружения.
Для шарикоподшипников радиальных однорядных параметр осевого нагружения e определяют по формуле из табл. 2,6 [2]
eа =0.574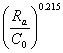 =
=![]() =0,314>0.3
=0,314>0.3
eB =0.574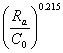 =
=![]() =0,327>0.3
=0,327>0.3
3. Осевые составляющие от радиальных нагрузок.
При нагружении шарикового радиально-упорного подшипника радиальной нагрузкой Ra, Rв возникают осевые составляющие:
![]()
![]()
4. Внешние осевые силы, действующие на подшипники.
Условие
равновесия вала под действием приложенных к нему осевых сил запишем в виде ![]()
Поскольку для данной схемы нагружения выполняется неравенство
![]()
то внешние осевые силы, действующие на подшипники, определяются по формулам
![]() ;
; ![]()
5. Коэффициент нагрузки
Если ![]()
![]() e следует принять X=1, Y=0. При
e следует принять X=1, Y=0. При ![]() >e для этих
подшипников принимают X = 0.45, Y =
>e для этих
подшипников принимают X = 0.45, Y = ![]()
Окончательно получим ![]() >e
>e
X = 0.45 Y = ![]()
Тогда эквивалентная динамическая нагрузка
P = ![]() = 4,9 кН
= 4,9 кН
Долговечность подшипника при максимальной нагрузке, ч:
Lh=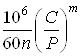 =
= 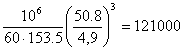
где m=3 показатель степени кривой усталости для шарикоподшипников.
Если задан типовой режим нагружения, то эквивалентная долговечность подшипника
LE = ![]() ,
,
где ![]() h – коэффициент
эквивалентности, определяемый по табл. 12 [2] в зависимости от типового режима
нагружения:
h – коэффициент
эквивалентности, определяемый по табл. 12 [2] в зависимости от типового режима
нагружения:
![]() h=0,18 LE
=
h=0,18 LE
= ![]() ч.
ч.
Для подшипников зубчатых редукторов должно выполняться
условие LE
![]() 10000 ч.
10000 ч.
5. Расчет вала на усталостную прочность
5.1 Моменты и силы в опасном сечении
2. Суммарный изгибающий момент
M=![]() = =
= =![]() Нм
Нм
где MZ- изгибающий момент в горизонтальной плоскости, MZ=67.7 Н×м; MY - изгибающий момент в вертикальной плоскости MY = 98.2 Н×м.
Осевая сила Fa =0.659кН
2. Геометрические характеристики опасного сечения
Значения площади поперечного сечения A, осевого ![]() и полярного
и полярного ![]() моментов
сопротивлений для типовых поперечных сечений определяют по формулам.
моментов
сопротивлений для типовых поперечных сечений определяют по формулам.
Для сплошного круглого вала
A =![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ;
;
Для сечения с одним шпоночным пазом:
A =![]() ,
, ![]() =
=![]() –
– ![]() ,
, ![]() =
=![]() –
– ![]() ,
,
где b – ширина; t1 – глубина шпоночного паза на валу (табл. 8 [2]),
b= 14 мм t1= 5,5 мм
A = ![]() =
=![]() мм
мм![]()
![]() =
=![]() –
– ![]() =
=![]() мм
мм![]()
![]() =
=![]() –
– ![]() =
=![]() =16557 мм
=16557 мм![]()
4. Суммарный коэффициент запаса прочности
Определяем по формуле (2) [2]:
S =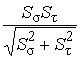
где ![]() и
и ![]() - коэффициенты запаса
прочности по нормальным и касательным напряжениям.
- коэффициенты запаса
прочности по нормальным и касательным напряжениям.
Условие прочности вала имеет вид
S![]() [S]
[S]
где [S] – допускаемый коэффициент запаса прочности.
Рекомендуемое значение [S] =2…2.5.
Значения ![]() и
и ![]() определяют по формулам
определяют по формулам
![]() =
=
![]() =
=
где ![]() и
и ![]() – пределы выносливости
материала при симметричном цикле изгиба и кручения;
– пределы выносливости
материала при симметричном цикле изгиба и кручения; ![]() и
и
![]() - амплитуды напряжений
цикла;
- амплитуды напряжений
цикла; ![]() и
и ![]() - средние напряжения цикла,
- средние напряжения цикла,
![]() и
и ![]() – коэффициенты перехода от
пределов выносливости образца к пределам выносливости детали,
– коэффициенты перехода от
пределов выносливости образца к пределам выносливости детали, ![]() и
и ![]() - коэффициенты
чувствительности к асимметрии цикла.
- коэффициенты
чувствительности к асимметрии цикла.
Значения ![]() и
и ![]() равны:
равны:
![]() = 0.02 (1+0.01
= 0.02 (1+0.01![]() ) =0,02 (1+0,01*890)=0,198
) =0,02 (1+0,01*890)=0,198
![]() = 0.5
= 0.5![]() =0,5*0,198=0,099
=0,5*0,198=0,099
Пределы выносливости материала при симметричном цикле изгиба и кручения определяются по следующим формулам:
для углеродистых
сталей ![]() = 0.43
= 0.43![]() =0,43*890=382,7 МПа
=0,43*890=382,7 МПа
![]() = 0.58
= 0.58![]() =0,58*382,7=222 МПа
=0,58*382,7=222 МПа
При вычислении амплитуд и средних напряжений цикла принимают, что напряжения изгиба меняются по симметричному циклу, а касательные по наиболее неблагоприятному отнулевому циклу. В этом случае
![]() =
= =
=![]() МПа
МПа
![]() =
=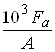 =
=![]() МПа
МПа
![]() =
=![]() =
=![]() =
=![]() МПа
МПа
5. Коэффициенты
![]() = (
= (![]() +KF -1)/KV,
+KF -1)/KV, ![]() = (
= (![]() +KF -1)/KV,
+KF -1)/KV,
Для посадки с
натягом ![]() определяется методом
линейной интерполяции по (табл7,5 [])
определяется методом
линейной интерполяции по (табл7,5 [])
![]() =4,5;
=4,5; ![]()
где ![]() и
и ![]() – эффективные коэффициенты
концентрации напряжений
– эффективные коэффициенты
концентрации напряжений
![]() и
и ![]() - коэффициенты влияния
размера поперечного сечения вала;
- коэффициенты влияния
размера поперечного сечения вала;
KF – коэффициент влияния
шероховатости поверхности, определяется по табл. 5,5 [2] в зависимости от ![]() , примем что поверхность
вала под зубчатое колесо получена чистовым обтачиванием тогда:
, примем что поверхность
вала под зубчатое колесо получена чистовым обтачиванием тогда:
![]() =3,2 мкм KF=1,25
=3,2 мкм KF=1,25
KV – коэффициент влияния упрочнения.
При отсутствии упрочнения поверхности рассчитываемого участка вала принимают KV =1.
В результате расчета получили:
![]() =
=![]() ;
; ![]() =
=![]()
![]() =
=![]() ;
; ![]() =
=![]()
Тогда общий коэффициент запаса прочности будет равен:
S =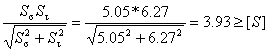
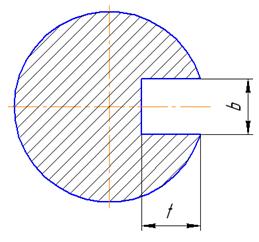
6. Шпоночное соединение
Длину шпонки назначают из стандартного ряда, принимая ее на 5…10 мм меньше длины ступицы. Размеры шпонки в поперечном сечении, а также размеры шпоночных пазов на валу и ступицы определяются диаметром вала по (табл. 1,8 [2])
Исходные данные
Диаметр вала dв=45 мм
Ширина шпонки b=14 мм
Высота шпонки h= 9 мм
Глубина паза на валу t1=5,5 мм
На ступице t=3,8 мм
Крутящий момент T3=332 Нм
1. Расчет призматических шпонок выполняется как проверочный на смятие по формуле
![]()
Где Т3 – крутящий момент на участке вала со шпоночным пазом, Нм
h – высота шпонки; t1 – глубина паза на валу; lр – рабочая длина шпонки;
[![]() ] – допускаемое
напряжения смятия.
] – допускаемое
напряжения смятия.
lр=l – b = 31 мм
где l – длина шпонки; b – ширина шпонки.
Тогда
![]()
Для стальных
ступиц при нереверсивном приводе ![]() =150МПа при реверсивном
=150МПа при реверсивном ![]() =120 МПа
=120 МПа
Заключение
В конструкторской части проекта рассчитана двухступенчатая зубчатая передача с межосевым расстоянием первой (быстроходной) ступени 180 мм, передаточным числом первой ступени 5,6, межосевым расстоянием второй (тихоходной) ступени 225 мм, передаточным числом второй ступени 3,55.
Расчеты передач, валов удовлетворяют условиям прочности, чем подтверждается работоспособность конструкции.
В проектной части выполнены чертежи общего вида редуктора, рабочие чертежи тихоходного вала, колеса и корпусной детали. Для сборочного чертежа составлена спецификация.
Данный проект является учебным. Полученные знания по расчету проектирования будут использованы при изучении спец дисциплин и выполнении выпускной квалификационной работы.
Список литературы
1 Курсовое проектирование деталей машин / Чернавский С.А., Боков К.Н., Чернин И.М., Ицкович Г.М., Козинцов В.П. – 3-е изд., стереотипное. Перепечатка с издания 1987 г. – М.: ООО ТИД «Альянс», 2005. – 416 с.
2 Баранов Г.Л. Расчет деталей машин. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. – 172 с.
3 Березовский. Детали машин.
4 Эйдинов М.С. Конспект лекций по деталям машин
5 Иванов. Детали машин