Курсовая работа: Вивчення поняття відносин залежності

Курсова робота

Вивчення поняття відносин залежності

Зміст

Введення

1. Визначення й приклади

2. Простір залежності

3. Транзитивність

4. Зв'язок транзитивних відносин залежності з операторами замикання

5. Матроїди

Висновок

Список літератури

Введення

Метою курсової роботи є вивчення поняття відносини залежності, розгляд відносини залежності на різних множинах.

Поставлена мета припускає рішення наступних задач:

Вивчити й дати визначення поняттю відношення залежності.

Розглянути деякі приклади відносини залежності.

Сформулювати й довести властивості й теореми як для довільних, так і для транзитивних просторів залежності.

Розглянути теорему про зв'язок транзитивного відношення залежності й алгебраїчного оператора замикання.

Вивчити поняття матроїда, привести приклади матроїдів.

Розглянути жадібний алгоритм і його зв'язок з матроїдами.

На підставі поставлених цілей і задач кваліфікаційна робота розбивається на 5 параграфів.

У першому параграфі наведені основні визначення й розглянуті деякі приклади відносини залежності.

У другому - розглядаються довільні простори залежності, їхньої властивості й деяких теорем.

Третій – присвячений транзитивним і кінцеве мірним просторам залежності. Тут розглянуті властивості транзитивних просторів залежності й доведені теореми, які підтверджують існування базису й інваріантність розмірності в будь-якому кінцеве мірному транзитивному просторі залежності.

У четвертому параграфі формулюються основні визначення дотичного оператора замикання й розглянута теорема про подання транзитивного відношення залежності за допомогою алгебраїчного оператора замикання.

П'ятий параграф присвячений матроїдам, прикладам матроїдів і їхньому застосуванню при вивченні теоретичною основою аналізу «жадібних» алгоритмів.

Основною літературою при написанні кваліфікаційної роботи стали монографії: Кона П. «Універсальна алгебра» [2] і Куроша О. Г. «Курс вищої алгебри» [3].

1. Визначення й приклади

Визначення 1.

Множина Z підмножин множини A назвемо відношенням залежності на A, якщо виконуються наступні аксіоми:

Z₁:  Z ;

Z₂:  Z  Z ;

Z₃:  Z ( Z - звичайно).

Підмножина множини A називається залежною, якщо вона належить Z, і незалежною у противному випадку.

Легко переконатися в незалежності аксіом Z₁ - Z₃..

Модель 1: . Думаємо Z = B (А) для будь-якої множини .

Модель 2: . Нехай Z =  при .

Модель 3: . Нехай Z =  для нескінченної множини .

Визначення 2.

Простором залежності назвемо пари  Z , де Z – відношення залежності на A.

Визначення 3.

Елемент  називається залежним від множини , якщо а Î X або існує така незалежна підмножина Y множини X, що  залежно, тобто  Z  Z ).

З визначення 1 випливає, що якщо елемент  залежить від множини , то він залежить від деякої кінцевої підмножини .

Визначення 4.

Множина всіх елементів, що залежать від X, називається оболонкою множини X і позначається через .

Ясно, що  й включення  тягне включення їхніх оболонок: .

Визначення 5.

Якщо  = A, то X називається множиною, що породжує, множини A.

Визначення 6.

 Незалежна підмножина, що породжує, множини A називається базисом множини A.

Визначення 7.

Множина  залежить від , якщо будь-який елемент із  залежить від , тобто .

Визначення 8.

Відношення залежності Z на A будемо називати транзитивним відношенням залежності, якщо  .

Визначення 9.

 Транзитивним простором залежності назвемо простір залежності, у якому відношення залежності має властивість транзитивності.

Як теоретико-множинний постулат будемо використовувати наступний принцип, еквівалентний відомій аксіомі вибору.

Лема Цорна.

Непуста впорядкована множина, у якому кожне лінійно впорядкована підмножина має верхню грань, має максимальний елемент.

Далі доцільно розглянути деякі приклади відносини залежності:

Приклад 1.

Поняття лінійної залежності у векторному просторі V над полем . Система векторів векторного простору V називається лінійно залежної, якщо існує кінцева лінійно залежна її підсистема, у противному випадку – лінійно незалежної.

Поняття лінійної залежності в кінцеве мірних векторних просторах дається в курсі алгебри. Кінцева система векторів V називається лінійно залежної, якщо існують елементи поля  одночасно не рівні нулю й такі, що лінійна комбінація . Множина лінійних комбінацій множини  векторів векторного простору V з коефіцієнтами з поля P називається лінійною оболонкою цих векторів і позначається . При цьому  - є підпростором у просторі V, породженим . Одержуємо транзитивне відношення залежності.

Приклад 2.

Нехай поле  є розширенням основного поля Р, а  мінімальне підкольце утримуючі елементи  й поле Р. Підкольце  складається із всіх елементів поля, які виражаються через елементи  й елементи поля Р за допомогою додавання, вирахування й множення: це будуть усілякі багаточлени від  з коефіцієнтами з поля Р. Тоді, якщо для всякого елемента  існує єдиний запис у вигляді багаточлена від  як невідомих з коефіцієнтами з поля Р, тобто якщо різні багаточлени від  будуть різними елементами підкольца , те система елементів , буде називатися алгебраїчно незалежної над полем Р, у противному випадку алгебраїчно залежної. Довільна множина елементів поля Р називається залежним, якщо воно містить кінцеву залежну підмножину. У першому випадку кільце  ізоморфно кільцю багаточленів . Відношення алгебраїчної залежності над полем Р є транзитивним відношенням залежності.

Приклад 3.

Нехай на множині A задане рефлексивне й симетричне бінарне відношення  (називане відношенням подібності). Підмножина X множини A будемо вважати залежним, якщо воно містить два різних елементи, що перебувають у відношенні .

Оболонкою множини  служить множина

У цьому випадку можна підсилити аксіому  відносини залежності в такий спосіб:

 Z  Z.

 Тоді оболонкою множини  буде множина всіх елементів, що перебувають відносно подібності хоча б з одним елементом із множини .

Уведене відношення залежності буде транзитивним тоді й тільки тоді, коли відповідне бінарне відношення  буде транзитивне, тобто є відношенням еквівалентності на .

У випадку, коли  - відношення еквівалентності  буде незалежним тоді й тільки тоді, коли  множина  містить не більше одного елемента. Будь-яка максимальна незалежна підмножина буде містити рівно по одному елементі з кожного класу еквівалентності .

Приклад 4.

Розглянемо чотирьох елементну множину .

Назвемо підмножину  множини  залежним тоді й тільки тоді, коли  або .

Z .

Розглянемо підмножину  множини , по уведеному визначенню воно буде незалежно. Розглянемо оболонку множини   й знайдемо оболонку оболонки нашої множини . Таким чином, ми одержали, тобто розглянуте нами відношення залежності не є транзитивним.

Приклад 5.

Розглянемо довільну множину  й . Множина  будемо вважати залежним, якщо  B (А)\ B (В), тобто , але . Таким чином, одержали наступний транзитивний простір залежності:  B (А)\ B (В. Оболонкою  буде множина .

Зокрема можна розглянути 2 випадки:

, тобто всі множини незалежні, тоді  .

 B (А) , тобто всі множини, крім порожнього, будуть залежними, у цьому випадку  .

Приклад 6.

Розглянемо довільну множину  і його непусту кінцеву підмножину . Уведемо на множині А наступне відношення залежності

Z B (А) .

Таким чином, залежними будуть всі надмножини множини .

Якщо , то .

Якщо , то .

Якщо , то .

Одержуємо транзитивний простір залежності.

Приклад 7.

Підпростір простору залежності  Z . Розглянемо , де діє те ж відношення залежності Z. Тоді одержимо індукований простір залежності  Z  B . У цьому випадку залежними будуть тільки ті підмножини множини, які були залежні в просторі  Z . І якщо простір  Z транзитивне, те транзитивним буде й підпростір .

Приклад 8.

Нехай  і Z = . Такий простір залежності  Z не транзитивне, тому що  й . Простір А має два базиси  й, які є і єдиними мінімальними множинами, що породжують в.

Цей приклад показує, що існують не транзитивні простори залежності, у яких мінімальні множини, що породжують, незалежні, тобто є базисами.

Приклад 9.

Задамо на множині N натуральних чисел наступне відношення залежності:

Z .

Одержуємо нескінченну строго зростаючий ланцюжок оболонок в  Z . При  одержуємо

.

Таким чином, маємо .

Зауваження.

Поняття простору залежності можна й зручно визначати через базу залежності. Саме, множина B всіх мінімальних залежних множин простору залежності  Z назвемо його базою. Ясно, що множини з B не порожні, кінцеві й не втримуються друг у другу. Крім того, будь-яка незалежна множина містить деяка множина бази B. Простір  Z має єдину базу й однозначно визначається їй. Тому простору залежності можна задавати базами.

Легко бачити, що вірно наступне твердження:

Непуста множина B підмножин множини  задає на  відношення залежності тоді й тільки тоді, коли множини з B не порожні, кінцеві й не включений друг у друга.

У термінах бази B можна сформулювати умова транзитивності відповідного простору залежності.

2. Простір залежності

Теорема 1.

Нехай  Z - довільний простір залежності. Розглянемо наступні три твердження:

X — базис в A;

X — максимальна незалежна підмножина в A;

 X — мінімальна множина, що породжує, в A.

Тоді  й .

Доказ:

(i)  (ii)     Якщо X – базис, то по визначенню 6 X – незалежна підмножина, що породжує. Доведемо від противного, що воно максимальне. Нехай існують незалежні множини . Візьмемо , тоді  незалежно, тому що будь-яка підмножина незалежної множини незалежно. Тому по визначеннях 3 і 5 , звідки , одержали протиріччя з умовою. Тому X є максимальною незалежною підмножиною в A.

(ii)  (i)     Доведемо від противного, нехай  не базис в , тобто . Тоді  таке, що незалежно й лежить в , одержали протиріччя з максимальністю .

(ii)  (iii) Якщо X — максимальна незалежна множина в A, те всякий елемент в A або належить X, або такий, що залежно, а тому  в тім і іншому випадку, тобто  Оскільки , те X - множина, що породжує. Виходить,  - базис простору .

Доведемо тепер, що воно мінімально. Нехай множина . Доведемо, що воно не є породжує для A. Візьмемо , але . Тоді  незалежно, як підмножина множини X. Тому по визначеннях 3 і 5  і , а це значить, що Y не є множиною, що породжує. Висновок: X – мінімальна множина, що породжує, в A.

(i)  (iii) Справедливо, по доведеним вище твердженнях (i) (ii) і (ii) (iii). :

Визначення - позначення 10.

Для довільної множини  простору залежності  Z позначимо  множину всіх максимальних незалежних підмножин, а через  - множину всіх мінімальних підмножин, що породжують, цієї множини.

З теореми 1 випливає, що  збігається із множиною всіляких базисів простору  й  для кожного .

Наступний приклад показує, що зворотне включення  вірно не завжди.

Приклад 10.

Розглянемо дев'яти елементну множину , що записана у вигляді матриці . Залежними будемо вважати підмножини множини , що містять «прямі лінії»: стовпці, рядки або діагоналі матриці .

Розглянемо множини  й , вони буде максимальними незалежними, тому що не містять прямих і при додаванні будь-якого елемента з , що не лежить у них, стають залежними. Тут максимальні незалежні множини містять різна кількість елементів.

Розглянемо ще одну множину , вона є мінімальним що породжує, тому що якщо виключити з нього хоча б один елемент, то воно вже не буде множиною, що породжує. Легко помітити, що  залежно, тому не є базисом. Даний приклад ілюструє, що (iii) (i) не вірно в загальному випадку, тобто для довільних просторів залежності.

Для будь-якого простору залежності  Z виконуються наступні властивості:

Заміщення. Якщо

Доказ:

Нехай , . Тому що  залежить від , те  залежить від незалежної підмножини  множини , тобто  залежно. Тепер, якби , те  було б підмножиною множини  й тому , що суперечило б нашому припущенню. Тому . Візьмемо . Тоді  незалежно, тому що . Але  залежно. Звідки .

Вкладеність. Об'єднання будь-якої системи вкладених друг у друга незалежних множин є незалежною множиною, тобто  - незалежно, де  також незалежні й

Доказ:

Доведемо від противного. Припустимо, що  залежно, тоді в ньому найдеться кінцева залежна підмножина : . Маємо , одержали протиріччя з незалежністю .

Максимальність. Будь-яка незалежна множина втримується в максимальній незалежній множині.

Доказ:

Нехай  - довільна незалежна множина в.  Утворимо множину  Z : всіх незалежних множин, що містять . Відносно  множина  є впорядкованою множиною, що задовольняє по властивості вкладеності, умові леми Цорна. Тоді по лемі Цорна в  існує максимальний елемент .

Теорема 2.

Будь-який простір залежності має базис.

Доказ:

Візьмемо порожню множину, вона незалежне. По властивості максимальності воно повинне втримуватися в деякій максимальній незалежній множині, що по теоремі 1 є базисом.

3. Транзитивність

Особливий інтерес представляють транзитивні простори залежності. Важливим результатом є доказ інваріантності розмірності будь-якого транзитивного простору залежності.

Доведемо деякі властивості, справедливі для транзитивних просторів залежності  Z .

Властивість 1:  залежить від .

Доказ:

 залежить від , тобто  , і . Розглянемо , тоді  - незалежно й  - залежно, а , одержуємо, що , тому . Маємо .

По визначенню 8 будь-яка підмножина  залежить від  

Властивість 2: Якщо  залежить від , а  залежить від , те  залежить від .

Доказ:

Запишемо умову, використовуючи властивість 1 , а , тоді очевидно, що .

Властивість 3: Якщо X — мінімальна множина, що породжує, в A, те X - базис в A.

Доказ:

Нехай X — мінімальна множина, що породжує, в A. Покажемо, що воно не може бути залежним, тому що в цьому випадку його можна було б замінити власною підмножиною, що усе ще породжує A. Дійсно, у силу транзитивності відносини залежності, будь-яка множина, що породжує множина X, буде так само породжувати й множина A. Отже, X - незалежна множина, що породжує, що по визначенню 6 є базисом.

Властивість 4:  для кожного .

Доказ: Потрібне із властивості 3.

Властивість 5 (про заміну.) :

Якщо X — незалежна множина й Y — множина, що породжує, в A, то існує така  підмножина множини Y,  що  й - базис для A.

Доказ:

Розглянемо систему J таких незалежних підмножин Z множини A, що .

Тому що X незалежно, те такі множини існують; крім того, якщо — деяке лінійно впорядкована множина множин з J, те його об'єднання  знову належить J, оскільки Z задовольняє умові , і якщо Z залежне, те деяка кінцева підмножина множини Z повинне було б бути залежним; ця підмножина втримувалося б у деякій множині  в суперечності з тим фактом, що всі  незалежні.

По лемі Цорна J має максимальний елемент М; у силу максимальності кожний елемент множини Y або належить М, або залежить від М, звідки . Цим доведено, що М — базис в A. Тому що , те М має вигляд , де  задовольняє умовам .■

Визначення 11.

Простір залежності  Z називається кінцеве мірним, якщо будь-яке його незалежна множина кінцева.

Теорема 3.

Нехай  Z - транзитивний простір залежності. Тоді будь-які два базиси в цьому просторі рівно потужні.

Доказ:

Розглянемо спочатку випадок кінцеве мірного простору .

Нехай В, З — будь-які два базиси в А, їхнє існування забезпечується теоремою 2, і , , , де різні елементи позначені різними буквами або постачені різними індексами. Застосуємо індукцію по max (r, s).

Якщо r = 0 або s = 0, то або , і . Тому можна припускати, що r ≥ 1, s ≥ 1, без обмеження спільності будемо вважати, що r > s, так що насправді r > 1.

Припустимо, що базиси будуть рівне потужними для будь-якого t < r

По лемі про заміну множина  можна доповнити до базису D елементами базису З, скажемо

, t ≤ s < r.

Тепер перетинання D c У складається з n + 1 елемента, і D містить, крім того, ще t (< r) елементів, тоді як У містить, крім цього перетинання, ще r - 1 елементів, так що по припущенню індукції , тобто .

Оскільки r > 1, звідси випливає, що t ≥ 1, і тому перетинання D із Із містить не менше ніж n+1 елементів. Використовуючи ще раз припущення індукції, знаходимо, що  й, отже, r = s і базиси В и С рівне потужні.

Далі, нехай В - кінцевий базис в.  Тоді й будь-який інший базис Із простору  буде кінцевим. Дійсно, У виражається через кінцеву множину елементів  у силу транзитивності  буде що породжує й незалежною множиною в , тобто .

Нарешті, якщо базиси В и С нескінченні. Кожний елемент із У залежить від деякої кінцевої підмножини базису З, і навпаки. Потужність множини всіх кінцевих підмножин усякої нескінченної множини дорівнює потужності самої множини. Тому потужності В и С збігаються.

Теорема 4.

Нехай  Z - довільний простір залежності, тоді наступні умови еквівалентні

Z транзитивне;

для будь-якого кінцевого  ;

 кінцевих і Z

 Z;

для будь-якого кінцевого .

Доказ:

(i)  (ii)     Справедливо по теоремі 3 і прикладу 7.

(ii)  (iii)   Візьмемо , так що  - незалежно й . Допустимо, що твердження  Z невірно. Тоді  Z. Розглянемо . Маємо . Але  Z, тому  Z . По (ii) маємо . Але  - протиріччя.

(iii)  (ii) Доведемо від противного. Нехай . Можна вважати, що . Тоді по (iii)  незалежно. Одержали протиріччя з максимальністю

(iii)  (i)    Потрібно довести рівність  для довільного .

Візьмемо  й покажемо, що  Тому що , те  Нехай існує , тоді  незалежно й існує  Z і  Z . Розширюючи  в  можна припустити, що  По (ii) , тобто . Тому по (iii) Z . бачимо, що . Виходить, . Одержуємо протиріччя з тим, що  Отже, , те мережа .

Тепер досить показати, що . Нехай , тоді  залежно, розширюючи в  можна припустити, що , крім того , тоді по (ii) .  незалежно, тому . По (iii) Z . бачимо, що . Виходить, , одержали протиріччя з максимальністю . Отже, , зворотне включення очевидно, тому .

(iv) (ii) У силу теорем 1 і 3 і доведена еквівалентності

(i) (ii).■

Далі будемо розглядати транзитивний простір залежності  Z .

Визначення 12.

Потужність максимальної незалежної підмножини даної множини  називається рангом цієї множини: .

Будемо розглядати кінцеві підмножини .

Мають місце наступні властивості.

Властивість 1^о:  Z .

Доказ: Z .

Властивість 2^о: Z .

Доказ: Z, візьмемо , тоді по властивості 1^о  і . Зворотне твердження потрібне з визначення 13.

Властивості 3^о – 7^о сформульовані для .

Властивість 3^о: .

Доказ: Ясно, що , і тому що число елементів будь-якої підмножини не більше числа елементів самої множини, то дана властивість виконується.

Властивість 4^о: .

Доказ: потрібне з того, що незалежна підмножина в  можна продовжити до максимальної незалежної підмножини в ;

Властивість 5^о: .

Доказ:

Нехай  Тоді  И потім . Маємо  .

Властивість 6^о: .

Доказ: випливає із властивості 4⁰;

Властивість 7^о: .

Доказ:

.

4. Зв'язок транзитивних відносин залежності з операторами замикання

Транзитивне відношення залежності також може бути описане за допомогою алгебраїчного оператора замикання деякого типу. Для початку сформулюємо визначення використовуваних понять.

Визначення 13.

Множина E підмножин множини A називається системою замикань, якщо  E і система E замкнута щодо перетинань, тобто ∩D E для кожної непустої підмножини D E

Визначення 14.

Оператором замикання на множині A називається відображення J множини B (A) у себе, що володіє наступними властивостями:

J. 1. Якщо , то J(X) J(Y);

J. 2. X J(X);

J. 3. JJ(X) = J(X), для всіх X, Y B (A).

Визначення 15.

Оператор замикання J на множині A називається алгебраїчним, якщо для будь-яких  і   тягне  для деякої кінцевої підмножини  множини .

Визначення 16.

Система замикань називається алгебраїчної, якщо тільки відповідний оператор замикання є алгебраїчним

Слід зазначити теорему про взаємозв'язок між системами замикань і операторами замикань.

Теорема 5.

Кожна система замикань E на множині  визначає оператор замикання J на  за правилом J(X) = ∩{Y E | Y X}. Обернено, кожний оператор замикання J на  визначає систему замикань E  J .

Наступна теорема показує зв'язок транзитивного відношення залежності й алгебраїчного оператора замикання.

Теорема 6.

Для будь-якого транзитивного відношення залежності  Z відображення  є алгебраїчним оператором замикання на А із властивістю заміщення.

Обернено, будь-який алгебраїчний оператор замикання на А із властивістю заміщення виходить таким способом з деякого транзитивного відношення залежності Z на А.

Доказ:

Будемо називати підмножину Т множини A замкнутим, якщо .

Покажемо спочатку, що замкнуті підмножини утворять систему замикань. Якщо , де  - сімейство замкнутих множин, то нехай  - така незалежна підмножина множини B, що  залежно; оскільки  для всіх , маємо , звідки , тобто В замкнуто.

Нехай , те по визначенню 3  Z  кінцеве, таке що залежно. У першому випадку , а в другому . І оскільки  замкнуто в силу транзитивності, одержуємо алгебраїчний оператор замикання.

Цим доведено, що замкнуті підмножини утворять алгебраїчну систему замикань.

Виконання властивості заміщення потрібне з відповідної властивості просторів залежності.

Обернено, нехай  - алгебраїчний оператор замикання із властивістю заміщення.

Будемо вважати  залежним, якщо  для деякого , і незалежним у противному випадку.

Тому що оператор алгебраїчний, то звідси випливає, що всяка залежна множина має кінцеву залежну підмножину, і оскільки очевидно, що всяка множина, що містить залежну підмножину, саме залежно, у такий спосіб одержуємо відношення залежності. Умова транзитивності виконується по визначенню, і це показує, що ми маємо транзитивне відношення залежності.

Тепер для будь-яких ,  маємо  тоді й тільки тоді, коли  для деякої кінцевої підмножини  множини . Вибираючи  мінімальним, можемо припускати, що  незалежно. Звідси випливає, що  й, отже, .

Обернено, якщо , те знову  для деякої кінцевої незалежної підмножини  множини . Це означає, що  залежно, тобто  для якогось .

У силу властивості заміщення одержуємо, що  й , тому .

Зауваження. Існують алгебраїчні оператори замикання, що не володіють властивістю заміщення. Для приклада візьмемо нескінченну циклічну напівгрупу .

Нехай і . Тоді , , але .

5. Матроїди

Поняття матроїда тісно пов'язане з поняттям відносини залежності, тому ця тема розглядається в даній кваліфікаційній роботі. Однак з іншої сторони воно є теоретичною основою для вивчення й аналізу «жадібних» алгоритмів.

Визначення 17.

Матроїдом  називається кінцева множина й сімейство його підмножин , таке що виконується три аксіоми:

М₁: ;

М₂: ;

М₃:

Визначення 18.

Елементи множини  називаються незалежними, а інші підмножини   - залежними множинами.

Відповідно до уведеного раніше аксіомами простору залежності бачимо, що матроїди - це в точності кінцеві транзитивне простори залежності.

Розглянемо наступні приклади матроїдів:

Приклад 1.

Сімейство всіх лінійно незалежних підмножин будь-якої кінцевої множини векторів довільного непустого векторного простору є матроїдом.

Дійсно, по визначенню можна вважати, що порожня множина лінійно незалежно. Усяка підмножина лінійно незалежної підмножини векторів лінійно незалежно. Нехай  і - лінійно незалежні множини. Якби всі вектори із множини  виражалися у вигляді лінійної комбінації векторів із множини , то множина  була б лінійно залежним. Тому, серед векторів множини  є принаймні один вектор , що не входить у множину  й не виражається у вигляді лінійної комбінації векторів із множини . Додавання вектора  до множини  утворить лінійно незалежна множина.

Приклад 2.

Вільні матроїди. Якщо  - довільна кінцева множина, то  - матроїд. Такий матроїд називається вільним. У вільному матроїді кожна множина незалежно, А є базисом і .

Приклад 3.

Матроїд трансверсалей. Нехай  - деяка кінцева множина, і  - деяке сімейство підмножин цієї множини. Підмножина  називається часткової трансверсалью сімейства , якщо  містить не більш ніж по одному елементі кожної підмножини із сімейства . Часткові трансверсали над  утворять матроїд на А.

Перейдемо до розгляду жадібного алгоритму. Для початку потрібно сформулювати задачу, що будемо вирішувати з його використанням.

Нехай є кінцева множина , , вагова функція  й сімейство .

Розглянемо наступну задачу: знайти , де . Інакше кажучи, необхідно вибрати в зазначеному сімействі підмножина найбільшої ваги.

Не обмежуючи спільності, можна вважати, що

Розглянемо такий алгоритм, що вихідними даними має множину , сімейство його підмножин  і вагарню функцію , причому множина  впорядкована в порядку убування ваг елементів. Після виконання цього алгоритму ми одержимо підмножину .

Споконвічно шукана множина  порожньо, далі переглядаємо по черзі всі елементи із множини  й перевіряємо залежність множини , якщо  - незалежно, те елемент  додаємо в множину , якщо ж  - залежне, те переходимо до елемента , поки всі елементи із множини  не будуть перевірені.

Алгоритм такого типу називається «жадібним». Зовсім очевидно, що по побудові остаточна множина , тобто незалежно. Також очевидно, що жадібний алгоритм є надзвичайно ефективним: кількість кроків становить, тобто жадібний алгоритм є лінійним. (Не вважаючи витрат на сортування множини  й перевірку незалежності .)

Приклад 4.

Нехай дана матриця 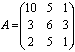. Розглянемо наступні задачі.

Задача 1. Вибрати по одному елементі з кожного стовпця, так щоб їхня сума була максимальна.

Тут вагова функція  ставить у відповідність елементу матриці  його значення. Наприклад, .

Множина  в такий спосіб:

.

Сімейство незалежних підмножин  будуть утворювати такі множини, у яких всі елементи з різних стовпців і порожня множина.

Наш алгоритм буде працювати в такий спосіб:

0 крок: ;

1 крок: перевіряємо для елемента , ;

2 крок: для , ;

3 крок: для , ;

4 крок: для , ;

5 крок: для , ;

6 крок: для , ;

7 крок: для , ;

8 крок: для , ;

9 крок: для , ;

У результаті одержали множину , ., отриманий результат дійсно є рішенням задачі.

Задача 2. Вибрати по одному елементі з кожного рядка, так щоб їхня сума була максимальна.

Тут функція  й множина  такі ж як і в попередній задачі, а сімейство незалежних підмножин  будуть утворювати такі множини, у яких всі елементи з різних рядків і порожня множина.

Використовуючи наш алгоритм одержимо наступне рішення: множина  й , що так само є вірним.

Задача 3. Вибрати по одному елементі з кожного стовпця й з кожного рядка, так щоб їхня сума була максимальною.

У цій задачі функція  й множина  залишаються колишніми, а сімейство незалежних підмножин  будуть утворювати такі множини, у яких всі елементи з різних стовпців і різних рядків і порожня множина.

Неважко бачити, що жадібний алгоритм вибере наступні елементи:

 і, які не є рішенням задачі, оскільки існує краще рішення -  і .

Виникає питання, у яких же випадках жадібний алгоритм дійсно вирішує поставлену задачу? На поставлене питання допоможе відповісти теорема, сформульована й доведена в [4, с.75-76].

Теорема 7.

 Для будь-якої функції  жадібний алгоритм знаходить незалежну множину  з найбільшою вагою, тоді й тільки тоді, коли  є матроїдом.

Дійсно, у нашім прикладі в задачах 1 і 2 - матроїд, а в задачі 3 таким не є, тому що не виконується аксіома М₃. Якщо розглянути  , тоді  одержали протиріччя з незалежністю хоча б одного із множин.

Висновок

У роботі були розглянуті такі питання, як:

Вивчення й визначення поняття відношення залежності.

Розглянуті деякі приклади відносин залежності.

Сформулювали й довели властивості теореми як для довільних, так і для транзитивних просторів залежності. Робота дала відповіді на всі питання, які були поставлені за мету.

Список літератури

1. Ван дер Варден Б.Л. Алгебра. – К., 2004

2. Кон П. Універсальна алгебра. – К., 2004.

3. Курош О. Г. Курс вищої алгебри. – К., 2003.

4. Новиков Ф. А. Дискретна математика для програмістів. – К., 2005

5. Фрид Е. Елементарне введення в абстрактну алгебру. – К., 2000