Реферат: Геометрия зрения, иллюзии. Морис Эшер
Государственное учреждение образования
«Гимназия имени Я. Купалы»
«Геометрия зрения, иллюзии. Морис Эшер.»
Ученика 7 «А» класса
Гимназии имени Я.Купалы
Трояна Артёма Александровича
Научный руководитель – учитель
математики высшей категории
Гимназии имени Я.Купалы
Чак Елена Николаевна
Мозырь-2010
Оглавление
Введение
1. Разновидности иллюзий.
2. Анатомия зрения
3. Иллюзии, связанные с особенностями строения глаза
3.1 Иррадиация
3.2 Слепое пятно
3.3 Астигматизм
4. Геометрия зрения
5. Оптические иллюзии
6. Ма́уриц Корне́лис Э́схер
6.1 Биографические сведения
6.2 Творчество
6.3 Математическая составляющая в работах Эшера
6.3.1 Невозможные фигуры
6.3.2 Визуальные парадоксы
6.3.3 Мозаика
6.3.4 Метаморфозы
6.3.5 Многогранники
6.3.6 Самовоспроизведение
Заключение
Литература
Введение
В гимназии я изучаю такой предмет, как геометрия. Это наука со своим специфическим методом познания мира, так как она изучает форму и взаимное расположение фигур в пространстве, их свойства. Это пространство, которое окружает нас. Все предметы в окружающем нас мире имеют три измерения, хотя не у всех можно указать длину, ширину, высоту Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творения природы и человека. Представители естественных наук, в частности физиков и астрономов всегда волновала надежность визуальных наблюдений.
Мы привыкли доверять собственному зрению, однако оно нередко обманывает нас, показывая то, чего в действительности не существует. В такие моменты мы сталкиваемся со зрительными иллюзиями - ошибками зрительного восприятия. Ученые создали немало обманчивых картинок, наглядно демонстрирующих, сколь ограничены возможности человеческого глаза.
Впервые увидев картины художника-одиночки Мориса Эшера я заинтересовался ими и решил исследовать математическую сторону иллюзий, проанализировать необычные работы художника.
Цель работы: объяснить зрительные иллюзии с точки зрения геометрии, увидеть и обосновать математическое начало в творчестве Мориса Эшера; углубить понимание природы зрения и восприятия в целом, в том числе иллюзорном.
Задачи исследования:
1. изучить теоретический материал по данной теме;
2. изучить и систематизировать картины Мориса Эшера;
3. найти примеры использования оптических иллюзий.
1. Разновидности иллюзий
Иллю́зия (лат. illusio — заблуждение, обман) — искаженное восприятие реально существующего объекта или явления. Иллюзии могут возникать у психически здоровых людей .
Разновидности иллюзий:
Физические — связаны с действующими в мире объективными законами физики (например, оптическая иллюзия: ложка, частично погруженная в стакан с водой, воспринимается как надломленная).
Оптические иллюзии — ошибки в зрительном восприятии, вызванные неточностью или неадекватностью процессов неосознаваемой коррекции зрительного образа.
Звуковые иллюзии.
Физиологические — связаны с особенностями периферических или центральных звеньев анализаторов (органов чувств) человека (например, если несколько раз поднять одновременно обеими руками пару различных по массе предметов, а затем другую пару предметов одинаковой массы, то предмет, оказавшийся в руке, в которой до того был более легкий, покажется более тяжелым, чем предмет, находящийся в другой руке).
Аффективные — возникают под влиянием выраженных колебаний настроения или в связи с остроформирующимся аффектом страха, тревоги.
Вербальные — возникают в результате искаженного восприятия реальных разговоров окружающих людей.
Органические (метаморфопсии) — искаженное зрительное восприятие формы, величины, цвета, пространственного расположения, состояния покоя или движения реально существующего предмета; различают аутометаморфопсии (ощущения изменения величины, формы частей собственного тела) и экзометаморфопсии (нарушения восприятия окружающих предметов); данный вид расстройств восприятия может наблюдаться не только у психически больных, но и у психически здоровых людей с патологией органа зрения.
Иллюзии осознаваемости (воплощенной осознаваемости) — ощущение, что рядом якобы кто-то находится; этот вид иллюзий выделен К. Ясперсом; по мнению автора, данный вид иллюзий является признаком формирования галлюцинаций и бреда.
Парейдолические (функциональные иллюзии) — особый вид иллюзий, при которых из сложных узоров (на ковре, зимнем стекле) возникают и постепенно развиваются сложные фантастические картины.
2. Анатомия зрения
То, о чем мы думаем как о чем-то, что мы видим, дает нам гораздо более достоверные сведения о нас самих, нежели об окружающем мире. И эта идея лежит в основе главнейших психологических и духовных учений мира.
Когда ученые объясняют феномен зрения, они часто начинают, сравнивают глаз с фотоаппаратом. Свет, подобно тому, как это происходит с линзами аппарата, попадает в глаз через небольшое отверстие — зрачок, расположенный в центре радужной оболочки глаза. Зрачок может быть шире или уже: таким образом, регулируется количество попадающего света. Далее свет направляется на заднюю стенку глаза — сетчатку, в результате чего в мозгу возникает определенная картинка (образ, изображение). Точно так же, когда свет попадает на заднюю стенку фотоаппарата, изображение фиксируется на пленку. Однако анатомия зрения не сводится к этому. Чтобы понять процесс сознательного визуального восприятия, необходимо исследовать и то, как человек, чтобы видеть, одновременно использует и глаза, и мозг, а для этого недостаточно простой аналогии с фотоаппаратом. Занимаясь изучением анатомии человеческого зрения, быстро обнаружим, что свет, проникая в глаза, способствует возникновению целого ряда явлений и процессов в нашем сознании, естественно, влияя на нашу жизнь в целом. Более того: хорошо видеть — не значит просто иметь острое зрение. Зрение формирует саму нашу жизнь, определяя не только то, насколько точно и отчетливо мы можем воспринимать свет, различать цвета и видеть те образы, что проходят перед нами, но и то, как мы проживаем собственную жизнь, что мы при этом испытываем и как взаимодействуем с окружающим миром.
Оптические обманы - не случайные спутники нашего зрения: они сопровождают его при строго определенных условиях, с неизменным постоянством закономерного явления и имеют силу для каждого нормального человеческого глаза. То, что человеку свойственно при известных обстоятельствах поддаваться иллюзиям зрения, обманываться относительно источника своих зрительных впечатлений, не следует вовсе рассматривать как всегда нежелательный недостаток, безусловный порок нашей организации, устранение которого было бы для нас во всех отношениях благотворно.

Что касается причин, обусловливающих ту или иную иллюзию зрения, то только для весьма немногих оптических обманов существует твердо установленное, бесспорное объяснение; к ним принадлежат те, которые обусловлены строением глаза: иррадиация, иллюзия Мариотта (слепое пятно), иллюзии, продолжаемые астигматизмом, и т. п.
Одна из самых известных оптико-геометрических иллюзий - иллюзия Мюллера-Лайера. Посмотрев на этот рисунок, большинство наблюдателей скажет, что левый отрезок со стрелочками наружу длиннее правого со стрелочками, направленными внутрь.
3. Иллюзии, связанные с особенностями строения глаза
Закрыть левый глаз и посмотреть правым на фигуру, изображенную слева, держа рисунок на расстоянии 15-20 см. от глаза. При некотором положении рисунка относительно глаза изображение правой фигуры перестает быть видимым.
3.1 Иррадиация
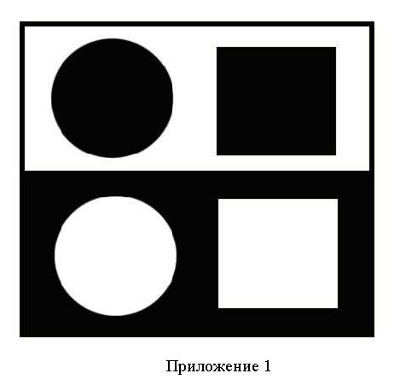
Рассмотрим одну из самых распространенных иллюзий (Приложение 1). При рассматривании издали белые фигуры внизу — круг и квадрат — кажутся крупнее черных, хотя те и другие равны. Чем больше расстояние, тем иллюзия сильнее. Явление это называется иррадиацией.
Иррадиация обусловлена тем, что каждая светлая точка предмета дает на сетчатке нашего глаза не точку, а маленький кружок (вследствие так называемой сферической аберрации); поэтому светлая поверхность окаймляется на сетчатке светлой полоской, увеличивающей занимаемое ею место. Черные же поверхности дают изображения, уменьшенные за счет светлой каймы окружающего фона.
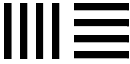
Эффектом иррадиации объясняется и различное впечатление от поверхностей, покрытых поперечными или продольными полосками. Поле с поперечными полосками кажется более низким, чем поле с продольными, так как белый цвет окружающий поля проникает наверху и внизу между полосками и визуально уменьшает высоту поля.
3.2 Слепое пятно
Естественные иллюзии появляются из-за особенностей в строении нашего зрительного аппарата. На поверхности сетчатки, у основания зрительного нерва, есть участок лишенный чувствительных к свету клеток. Лучи, приходящие в эту зону, не воспринимаются нами. Мы можем «терять» элементы окружающей нас картинки, если они совпадают со слепым пятном.
Чтобы подтвердить это явление проведем ряд экспериментов.
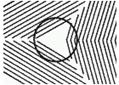
1. Рассматривая левым глазом крестик (Приложение 2) в правой части фигуры, мы на некотором расстоянии не увидим вовсе черного кружочка, хотя будем различать обе окружности. Круг совпал со слепым пятном.
2. Закрыв правый глаз, смотрите левым на верхний крестик (Приложение 2), с расстояния 20 - 25 сантиметров. Вы заметите, что средний большой белый кружок исчезает совершенно, хотя оба меньших кружка по бокам его хорошо видны. Если, не меняя положения рисунка, смотреть на нижний крестик, кружок исчезает только отчасти. Этот опыт носит имя своего создателя – Мариотта.
Исчезновение элементов в этих опытах обусловлено тем, что при указанном положении глаза относительно фигуры изображение кружка попадает на так называемое слепое пятно - место входа зрительного нерва, нечувствительное к световым раздражениям.
Известно, что Мариотт забавлял английского короля Карла II и его придворных тем, что учил их видеть друг друга без головы. Сетчатая оболочка глаза в том месте, где в глаз входит зрительный нерв, не имеет светочувствительных окончаний нервных волокон (палочек и колбочек). Следовательно, изображения предметов, приходящиеся на это место сетчатки, не передаются мозгу.
Вот интересный пример. На самом деле круг идеально ровный. Стоит прищуриться, и мы это видим.
3.3 Астигматизм
Астигматизмом - это неодинаковая выпуклость роговой оболочки глаза в различных направлениях (вертикальном, горизонтальном). Редкий глаз вполне свободен от этого несовершенства. Приблизительно 10% всех людей страдают врожденным астигматизмом.
Рассмотрим ещё одну иллюзию, связанную с астигматизмом. Эта фигура
(Приложение 3) дает другой способ обнаружить астигматизм глаза. Приближая ее к исследуемому глазу (закрыв другой), на некотором, довольно близком, расстоянии, сосредоточив взгляд на белом квадратике вверху, вы приблизительно через полминуты заметите, что нижняя белая полоса исчезнет (вследствие утомления сетчатки).
4. Геометрия зрения
С точки зрения геометрии линейная перспектива - это способ изображения фигур, основанный на применении центрального проектирования. Рассмотрим задачу построения перспективного изображения фигуры, которое называется центральной проекцией (от лат. projectio-бросание вперед).
Пусть выбрана плоскость проекций π, на которой строится изображение, и задан центр проекции - точка О, ей не принадлежащая. Тогда произвольная точка М фигуры будет проецироваться в точку М' пересечения прямой ОМ с плоскостью π. Ясно, что при разных положениях π получатся различные изображения одной и той же фигуры.
В живописи плоскость проекций (полотно картины) обычно находится между центром проекции (глазом художника) и объектом, так что точка М' оказывается между точками О и М. При этом плоскость π перпендикулярна предметной плоскости α, на которой располагаются изображаемые объекты.
Итак, каждому художнику, пишущему в реалистической манере, приходится решать геометрическую задачу на построение центральной проекции объектов на картинную плоскость. Очевидно, что точки основания картины (лежащие на линии пересечения плоскостей α и π ) проецируются в себя.

На рисунке показано, как получается изображение произвольной точки М плоскости α (цифры 1—4 указывают порядок проведения прямых).
Если точка К не лежит в предметной плоскости, то сначала из нее опускают перпендикуляр на α (на рис. это отрезок КМ), затем для его основания (точки М) выполняют построения 1—3. Наконец, проводят прямую КО, пересечение которой с плоскостью π и есть изображение точки К.
Вообще построение центральной проекции фигуры - задача не из простых. Она рассматривается в одном из разделов прикладной математики - начертательной геометрии изучающей пространственные фигуры при помощи построения их изображений на плоскостях проекций. Начертательная геометрия широко применяется в инженерном деле, строительной практике, в архитектуре и живописи.
Рассмотрим несколько примеров зрительных иллюзий, связанных с геометрическими фигурами.
1) Мы часто видим сходящиеся вдали параллельные линии (полотно железной дороги, шоссе и т. п.). Это явление называется перспективой.
Рассмотрим две «убегающие» от нас параллельные линии (трамвайные или железнодорожные). Они кажутся сходящимися в некоторой точке горизонта. При этом сама точка представляется нам бесконечно удаленной и недосягаемой. Зрение словно пытается убедить нас в том, что вопреки законам геометрии параллельные прямые пересекаются.

Эта иллюзия объясняется тем, что объект (шпала), находящийся на различных расстояниях от наблюдателя, виден под разными углами зрения и по мере удаления вдоль параллельных прямых (рельсов) его угловой размер уменьшается, что приводит к видимому уменьшению расстояния между линиями (в данном случае оно определяется величиной шпалы). Очевидно, когда угол зрения достигает некоторой "критической" величины, глаз перестает различать удаляющийся объект как тело, имеющее размеры, и прямые «сливаются» для него в одну точку.
Существует предельное значение угла зрения - наименьшее значение, при котором глаз способен видеть раздельно две точки.
2) Сравним относительные размеры нескольких находящихся в поле зрения предметов.
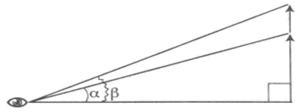
Если предметы удалены от глаз на одно и то же расстояние и расположены достаточно близко друг к другу, их сравнить легко. В этом случае мы редко ошибаемся в своей оценке: более высокий предмет виден под большим углом, поэтому и кажется выше.
Усложним задачу. Расположим предметы на разном расстоянии от глаза, в том числе предметы разного размера. Тогда их видимые размеры кажутся одинаковыми.
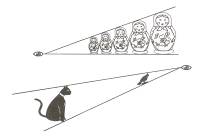
Выстроим, друг за другом по росту несколько матрешек, и посмотрим на них со стороны самой маленькой фигурки, а затем начнём медленно отходить назад, не изменяя при этом направления взгляда, то можно наблюдать, как матрешки будут постепенно «сливаться», загораживая друг друга. Наконец, на некотором расстоянии будет видна только одна из них - та, что расположена ближе остальных. Сместим фигурки в горизонтальных плоскостях, перпендикулярных направлению взгляда, таким образом, чтобы все они были полностью видны - матрешки кажутся одного размера.
Аналогичный опыт можно провести с любыми имеющимися под рукой предметами, расположив их на некотором расстоянии друг от друга, причем наибольшего визуального эффекта можно достичь, если использовать предметы, схожие по форме. В таком случае достаточно сравнить их линейные размеры: высоты, диаметры и т.д. Результат будет таким же.
Еще один наглядный пример, подтверждающий отмеченную закономерность, дает солнечное затмение, во время которого Луна полностью закрывает собой солнечный диск. В этот момент размеры обоих тел кажутся нам одинаковыми, поскольку Луна и Солнце видны с Земли под одним углом зрения.
На основе последнего равенства можно не только сравнить расстояния, а также относительные размеры двух объектов, наблюдаемых под одним углом зрения, но и найти любую из входящих в него величин по трем остальным. Независимо от формы предметов, наблюдаемое явление должно описываться «на языке математики» одним и тем же законом, в котором ключевую роль играют, такие параметры, как линейный размер и расстояние до предмета.
3) Определим высоту столба (вышки, дерева и т.п.).
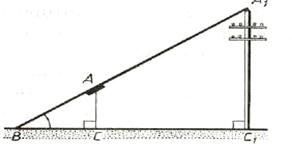
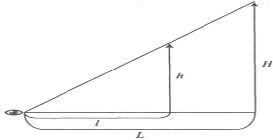
Отойдем от столба на расстояние, на котором больший палец вытянутой вперед руки закроет его полностью, (то есть их видимые размеры станут одинаковыми), подсчитав при этом число сделанных шагов. Для взрослого человека среднее расстояние от глаза до большого пальца вытянутой руки составляет 60 см, длина самого пальца - 7 см, а длина шага - 65 см. По этим данным легко вычислить примерную высоту столба. Аналогично определяется расстояние до недоступного объекта по его известной высоте. Отметим, что описанный способ надежен для оценки сравнительно близких расстояний до нескольких сотен метров; чем меньше предмет и чем дальше он находится, тем выше погрешность измерений.
С позиции геометрии, во всех приведенных примерах мы имеем дело с подобными фигурами или соответствующими отрезками, а именно высотами, различных по форме фигур; более того, в каждом случае мы сталкиваемся с преобразованием гомотетии, центр которой совпадает с глазом наблюдателя. Поэтому можно утверждать, что если два предмета видны под одним углом зрения, то их линейные размеры отличаются во столько же раз, во сколько раз отличаются расстояния до предметов:
![]()
5. Оптические иллюзии
Оптической иллюзией называется несоответствующее действительности представление видимого явления или предмета вследствие особенностей строения нашего зрительного аппарата. Попросту говоря - это неверное представление реальности.
Почему возникают оптические иллюзии? Зрительный аппарат человека - сложно устроенная система со вполне определенным пределом функциональных возможностей. В нее входят: глаза, нервные клетки, по которым сигнал передается от глаза к мозгу, и часть мозга, отвечающая за зрительное восприятие.
В связи с этим выделяются три основные причины иллюзии:
· наши глаза так воспринимают идущий от предмета свет, что в мозг приходит ошибочная информация;
· при нарушении передачи информационных сигналов по нервам происходят сбои, что опять же приводит к ошибочному восприятию;
· мозг не всегда правильно реагирует на сигналы, приходящие от глаз.
По происхождению оптические иллюзии делятся на три вида:
· естественные, или созданные природой (например, мираж);
· искусственные, или придуманные человеком (например, фокус “левитация” или, как говорят в народе, “летающая дама”;
· смешанные, то есть естественные иллюзии, воссозданные человеком (например, известные иллюзионные картинки, модель миража).
Виды иллюзий :
· двойственные;
· зрительное искажение;
· иллюзии цвета и контраста;
· восприятие размера;
· кажущиеся фигуры;
· невозможные фигуры;
· перевёрнутые картины;
· распознавание образа;
· соотношение фигур и фона.
6. Ма́уриц Корне́лис Э́схер
Творчество его нетривиально, фантастично.
6.1 Биографические сведения
Морис Корнелиус Эшер родился 17 июня 1898 года в Леевардене, административном центре голландской провинции Фрисландия. В доме, котором родился Эшер, сейчас находится музей.
В школе учился неважно. Оценки по всем предметам у Мориса были плохими за исключением рисования. Учитель рисования художник Самуэль де Мескита, оказавший на молодого человека огромное влияние (Эшер поддерживал дружеские отношения с Мескитой вплоть до 1944 года, когда Мескита, еврей по происхождению, был вместе с семьёй уничтожен нацистами), заметил талант у мальчика и научил его делать гравюры по дереву. Голландский мальчик - Мориц Корнелис Эшер с детства был немного странным. Бесцветный, замкнутый и заикающийся, он плохо учился и был подвержен двум маниям. Первую можно назвать "тягой к падению" - все вертикальные, устремляющиеся ввысь формы, имели для парня пугающую и одновременно восхитительную притягательность. Вторую манию можно назвать построением "безупречного бутерброда". В 1913 году Эшер в школе религии знакомится с парнем, по имени Бас Кист, который станет его лучшим другом. Оба интересовались технологией печати. В 1916 году Эшер выполняет свою первую графическую работу, гравюру на фиолетовом линолеуме - портрет своего отца Г. А. Эшера. С 19 лет Эшер посещает мастерскую художника Герта Стигемана, имевшего печатный станок. На этом станке были отпечатаны первые гравюры Эшера. Его отец, инженер-гидравлик, хотел, чтобы сын получил солидную профессию, и в 1919 году Эшер поступает в Гаарлемское училище архитектуры и декоративного искусства. В 1922 году, проучившись в училище два года, Эшер переезжает в Италию, где проживет 13 лет.
Каждое лето он путешествует по Южной Италии или Испании. Летние впечатления служат материалом для гравюр, над которыми он работает зимой. С 1941 года Эшер постоянно живет в Голландии. Всемирная известность пришла к нему в 1951 году после публикаций сразу в трех популярных журналах: «The Studio», «Time» и «Life». В 1954 году в Амстердаме состоялась большая выставка Эшера, приуроченная к Международному математическому конгрессу. Математики сразу признали художника «своим»; с этого времени его рисунки – неизменный атрибут физико-математических изданий. Среди его восторженных поклонников были и математики, которые видели в его работах оригинальную визуальную интерпретацию некоторых математических законов. Это более интересно тем, что сам Эшер не имел специального математического образования.
Однажды известный геометр Кокстер пригласил Эшера на свою лекцию, посвященную математическому содержанию его гравюр и литографий. К взаимному разочарованию, Эшер не понял почти ни слова из того, о чем рассказывал Кокстер. Вот что писал об этом сам художник: "Я так ни разу и не смог получить хорошей оценки по математике. Забавно, что я неожиданно оказался связанным с этой наукой. Поверьте, в школе я был очень плохим учеником. И вот теперь математики используют мои рисунки для иллюстрации своих книг. Представьте себе, эти ученые люди принимают меня в свою компанию как потерянного и вновь обретенного брата! Они, кажется, не подозревают, что математически я абсолютно безграмотен".
Слава мало изменила образ жизни художника, который продолжал упорно работать. Умер он 27 марта 1972 года.
6.2 Творчество
Одним из самых выдающихся аспектов творчества Эшера является изображение «метаморфоз», фигурирующих в разных формах во множестве работ. Художник подробно исследует постепенность перехода от одной геометрической фигуры к другой, посредством незначительных изменений в очертаниях. Кроме того, Эшер неоднократно рисовал метаморфозы, происходящие с живыми существами (птицы превращаются у него в рыб и проч.) и даже «одушевлял» в ходе метаморфоз неодушевлённые предметы, превращая их в живых существ.
Для сюжетов «классических» произведений Эшера («Рисующие руки», «Метаморфозы», «День и ночь», «Рептилии», «Встреча», «Дом с лестницей» ) характерно остроумное осмысление логических и пластических парадоксов. В сочетании с виртуозной техникой это производит сильнейшее впечатление. Многие графические и концептуальные находки Эшера вошли в число символов XX века и впоследствии неоднократно воспроизводились или «цитировались» другими художниками.
Морис Эшер одним из первых стал изображать в своих мозаичных картинах фракталы. Только спустя десятилетия учёные стали изучать свойста этих фигур и с помощью ЭВМ создавать то, что Эшер рисовал вручную.
6.3 Математическая составляющая в работах Эшера
Все же творчество Эшера интересно математикам не только потому, что в его работах можно обнаружить отголоски конкретных математических результатов. Скорее они вызывают ассоциации с общими математическими идеями. Платон считал, что абстрактные идеи живут отдельно в "мире чистых сущностей" (таковы идеи пространства и времени). В таком, платоновском понимании мир Эшера и мир математики.
Отец Морица однажды обнаружил рисунок своего сына, на котором был изображен... квадратный круг.
В процессе своей работы он черпал идеи из математических статей, в которых рассказывалось о мозаичном разбиении плоскости, проецировании трехмерных фигур на плоскость и неевклидовой геометрии.
6.3.1 Невозможные фигуры

Он был очарован всевозможными парадоксами и в том числе "невозможными фигурами". Парадоксальные идеи Роджера Пенроуза были использованы во многих работах Эшера. Наиболее интересными для изучения идеями Эшера являются всевозможные разбиения плоскости и логика трехмерного пространства. Эшер создал свою невозможную фигуру это квадрат. И использует его в своих картинах для создания большей загадочности и абсурда.


Невозможная лестница была первым невозможным объектом, который использовал Эшер в своём творчестве. В реальности не существует лестницы, по которой можно одниматься, спускаясь, как в его литографии «Восхождение и спуск» . Прямоугольник внутреннего двора замкнут стенами здания, у которого вместо крыши – бесконечная лестница по которой идут на встречу друг другу люди…
Если двигаться по лестнице по часовой стрелке, то мы будем постоянно подниматься, а если будем двигаться против часовой стрелки, то – спускаться.

Секрет здесь кроется в том, что в реальной модели невозможной лестницы должен быть разрыв в районе правого угла (на рисунке), которого в данном случае не видно, так как точка обзора выбрана намеренно, чтобы скрыть этот разрыв.
«Водопад» — литография голландского художника Эшера. Впервые была напечатана в октябре 1961 года. В этой работе Эшера изображен парадокс — падающая вода водопада управляет колесом, которое направляет воду на вершину водопада. Водопад имеет структуру «невозможного треугольника Пенроуза». Конструкция составлена из трёх перекладин, положенных друг на друга под прямым углом. Водопад на литографии работает как вечный двигатель. Но ведь, как известно из школьного курса физики, вечный двигатель невозможен! Как же Эшеру удалось с такими подробностями изобразить то, чего в природе вообще не может быть?! При попытке соорудить двигатель согласно чертежу "обман" всплывает сразу - в трехмерном пространстве такие конструкции геометрически противоречивы и могут существовать только на бумаге, то есть на плоскости, а иллюзия "объема" создается лишь за счет признаков перспективы (в данном случае - умышленно искаженных).
6.3.2 Визуальные парадоксы

Эшер понимал, что геометрия определяет логику пространства, но и логика пространства определяет геометрию. Одна из наиболее часто используемый особенностей логики пространства - игра света и тени на выпуклых и вогнутых объектах. На литографии "Куб с полосками" выступы на лентах являются визуальным ориентиром того, как расположены полоски в пространстве и как они переплетаются с кубом. И если вы верите своим глазам, то вы никогда не поверите тому, что нарисовано на этой картине. Большинство художников, экспериментирующие с логикой пространства, изменяют эти отношения между объектами, основываясь на своей интуиции, как, например, Пикассо.
6.3.3 Мозаика

Регулярное разбиение плоскости, называемое "мозаикой" - это набор замкнутых фигур, которыми можно замостить плоскость без пересечений фигур и щелей между ними. Обычно в качестве фигуры для составления мозаики используют простые многоугольники, например, квадраты или прямоугольники. Но Эшер интересовался всеми видами мозаик - регулярными и нерегулярными (прим. перев. нерегулярные мозаики образуют неповторяющиеся узоры) - а также ввел собственный вид, который назвал "метаморфозами", где фигуры изменяются и взаимодействуют друг с другом, а иногда изменяют и саму плоскость.
Интересоваться мозаиками Эшер начал в 1936 году во время путешествия по Испании. Он провел много времени в Альгамбре, зарисовывая арабские мозаики, и впоследствии сказал, что это было для него "богатейшим источником вдохновения".
Математики доказали, что для регулярного разбиения плоскости подходят только три правильных многоугольника: треугольник, квадрат и шестиугольник. (Нерегулярных вариантов разбиения плоскости гораздо больше. В частности в мозаиках иногда используются нерегулярные мозаики, в основу которых положен правильный пятиугольник.) Эшер использовал базовые образцы мозаик, применяя к ним трансформации, которые в геометрии называются симметрией, отражение, смещение и др. Также он исказил базовые фигуры, превратив их в животных, птиц, ящериц и проч. Эти искаженные образцы мозаик имели трех-, четырех- и шестинаправленную симметрию, таким образом сохраняя свойство заполнения плоскости без перекрытий и щелей. В гравюре «РЕПТИЛИИ» маленькие крокодилы играючи вырываются из тюрьмы двухмерного пространства стола, проходят кругом, чтобы снова превратиться в двухмерные фигуры. Мозаику рептилий Эшер использовал во многих своих работах.
6.3.4 Метаморфозы

Во всех работах Эшера используется ассиметричная геометрия. Он один из немногих умел на холсте изобразить «метаморфозы. Эшер рисовал метаморфозы, происходящие с живыми существами (птицы превращаются у него в рыб и прочее) и даже «одушевлял» в ходе метаморфоз неодушевлённые предметы, превращая их в живые существа. Не составляет особого труда заметить два основных объекта первого из них: это существа, обитающие в небе и воде - птица и рыба. При движении по рисунку снизу вверх, накапливаются несущественные, едва различимые отличия у сходных объектов – наращивается количественная определенность. Это приводит к новому объекту, совершенно не похожему на исходный.
6.3.5 Многогранники
Правильные геометрические тела - многогранники - имели особое очарование для Эшера. Во его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов. Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Они еще называются телами Платона. Это - тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями. На гравюре "Четыре тела" Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.




Большое количество различных многогранников может быть получено объединением правильных многогранников, а также превращением многогранника в звезду. Для преобразования многогранника в звезду необходимо заменить каждую его грань пирамидой, основанием которой является грань многогранника. Изящный пример звездчатого додекаэдра можно найти в работе «Порядок и хаос". В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором. Заметим также, что анализируя картину можно догадаться о природе источника света для всей композиции - это окно, которое отражается левой верхней части сферы.
Фигуры, полученные объединением правильных многогранников, можно встретить во многих работах Эшера. Наиболее интересной среди них является гравюра "Звезды", на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры. Таким образом нам необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством.
На гравюре "Четыре тела" Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.
6.3.6 Самовоспроизведение

Центральная идея самовоспроизведения, взятая на вооружение Эшером, обращается к загадке человеческого сознания и способности человеческого мозга обрабатывать информацию так, как не сможет обработать ни один компьютер. Литографии «Рисующие руки" и "Рыбы и чешуйки" используют эту идею разными способами. Самовоспроизведение является направленным действием. Руки рисуют друг друга, создавая самих себя. При этом сами руки и процесс их самовоспроизведения неразделимы. В работе "Рыбы и чешуйки" концепция самовоспроизведения представлена более функционально, и в данном случае она может быть названа самоподобием. В этом смысле данная работа описывает не только рыб, а все живые организмы, в том числе и человека. Конечно, мы не состоит из уменьшенных копий самих себя, но каждая клетка нашего тела несет в себе информацию обо всем теле в виде ДНК.
Углубляясь в изучение самовоспроизведения, можно его обнаружить в отражении и пересечении отражений реального мира. Такое пересечение встречается во многих картинах Эшера.
Заключение
90% информации приходит в наш мозг через глаза. Зная особенности зрения, человек может анализировать получаемую картинку, понимать, когда глаза его обманывают, а когда изображение полностью реально. Подобные знания могут существенно облегчить жизнь, избавив от неприятностей, связанных со зрительными обманами. Помогут лучше понимать некоторые природные явления, устройства некоторых предметов. Оптические иллюзии сопровождают нас в течение всей жизни. Поэтому знание основных их видов, причин и возможных последствий необходимо каждому человеку.
Анализ объяснения оптико-геометрических иллюзий показывает, что, во-первых, все параметры зрительного образа взаимосвязаны, благодаря чему и возникает целостное восприятие, воссоздается адекватная картина внешнего окружающего нас мира. Во-вторых, на восприятие влияют сформированные повседневным опытом стереотипы, например, представления о том, что мир трехмерен, начинающие работать, как только в картинку вносятся признаки, указывающие на перспективу.
Таким образом, мое исследование показало, сколь широка и многогранна деятельность человека, столь и различны требования, предъявляемые к форме и содержанию изображений. Одни из них должны производить на глаз человека такое же впечатление, какое производит и сам изображаемый предмет, иначе говоря, изображение должно обладать достаточной наглядностью. В другом случае изображение должно быть, в первую очередь, геометрически равноценно оригиналу, оно должно давать полную геометрическую и размерную характеристику изображаемого предмета.
Существует взаимовлияние в развитии геометрии и живописи; зрительные иллюзии существуют и их можно объяснить с помощью геометрии; оптические иллюзии использовались, и будут использоваться человеком в повседневной жизни.
При работе над темой я узнал много интересного о жизни замечательного голландского ученого художника Эшера. В работе я представил произведения художника разных лет и дал подробные описания использованных в них эффектов разбиения плоскости и трехмерного пространства, которые помогут учителям математики, истории, изобразительного искусства, информатики и физики при подготовке к урокам, внеклассным и факультативным занятиям, просто расширят кругозор. Эшера можно назвать художником одиночкой. Его работы трудно отнести к какому-либо художественному направлению. Эшер не много не дожил до компьютерной революции, но своими работами он доказал, что предвидел компьютерную графику.
Литература
1. Акбаев А.Н., Физика и живая природа. Ижевск: Удмуртский университет 1999.
2. Артамонов И. Д., Иллюзии зрения. М., 1961
3. Вадимов А. А., Тривас М.А.. Иллюзии зрения. М.: Наука, 1971.
4. Грегори Р.Л. Разумные глаза. М.2003г
5. Григорьева Н.Ю. Живая математика. М.2006г
6. Демьянов В.П. Геометрия и Марсельеза. М.1986г
7. Кагиров Р.Р. Ключи к местоположению визуального познания. Самара,2002г
8. Карпунина Н.М. Неожиданная математика. М.2003г
9. Луизов А. В.. Цвет и свет. Л.: Энергоатомиздат, 1989.
10. Перельман Я. И., Занимательная физика. Т.1,2. М.: Наука, 1983.
11. Розин В.М. Перспектива в геометрии и живописи. М. 1998 г
12. Франческа П. О живописной перспективе. Энциклопедия 2000г
13. Четверухин Н.Ф. Начертательная геометрия. М.1963г
14. Энциклопедия для детей. Художники Возрождения. М.2000 г
15. http.//mkesher.chaf.ru
16. http.//www.im-possible.info
17. http.//ru.wikipedia.org/wiki
18. . http.//rspu.edu.ru
19. http.//mkesher.chat.ru
20. http.//www.exposter.ru
21. http://gallery.artsportal.ru
Приложения


Приложение 4
( Иллюзия итальянского ресторана. Найдите 5 ошибок.)
| Методика изучения многогранников в школьном курсе стереометрии | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Вятский государственный ... Чаще всего в геометрии рассматривают связные фигуры, т. е. такие, в которых любые две точки можно соединить линией, целиком принадлежащей этой фигуре. В школьных учебниках после изучения "бесконечно-протяженных" и в силу этого весьма абстрактных геометрических фигур: прямых и плоскостей (вернее сказать, их взаимного расположения ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Художественные стилевые направления в искусстве | |
|
АНТИЧНОЕ ИСКУССТВО (от лат. antiquus - древний) - исторический тип искусства. Античностью называют эпоху Древней Греции и Рима. Этот термин впервые ... Голубой и зеленый цвета, эмоционально выражающие воздух и пространство, даль моря и бесконечность неба, были у греков всегда перед глазами, но в их живописи не использовались ... Плоскость стены зрительно дематериализуется за счет увеличения проемов окон, аркад, колонн, различных декоративных элементов. |
Раздел: Рефераты по культуре и искусству Тип: реферат |
| Исследование возможностей применения различных видов зрительных ... | |
|
Дипломная работа Исследование возможностей применения различных видов зрительных иллюзий в проектировании одежды для полных женщин Содержание ВВЕДЕНИЕ ... Третья причина - особенности мускульных усилий глаз, прикоторых возникает значительное увеличение мышечного усилия при повороте глаз в вертикальной плоскости сравнительно с ... Использование зрительных иллюзий, т. е. способности человеческого глаза воспринимать формы, фигуры, их части несколько иными, чем они на самом деле есть,- необходимое условие ... |
Раздел: Промышленность, производство Тип: дипломная работа |
| Изучение геометрии на уроках математики в 5-6 классах | |
|
Дипломная работа По теме: Изучение геометрии на уроках математики в 5-6 классах Оглавление: Введение Глава 1. Роль изучения геометрии в формировании ... 5. В преподавании основное внимание уделялось геометрии плоских фигур, рассматриваемых в пространстве, и меньше внимания - стереометрии. Неопределяемыми понятиями геометрии являются: точка, прямая и плоскость. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Аллегория в изобразительном искусстве | |
|
Витебский государственный университет им. П.М. Машерова Художественно - графический факультет Кафедра изобразительного искусства Курсовая работа на ... В аттике расположены четыре аллегорические фигуры, судя по атрибутам - Арифметика, Геометрия, Астрономия, Музыка. Просвечивая через тонкую лепку фигур второго плана, черный фон создает иллюзию светотени и воздушного пространства пейзажа. |
Раздел: Рефераты по культуре и искусству Тип: курсовая работа |