Учебное пособие: Характеристика анализа временных рядов
Министерство образования и науки Украины
Севастопольский государственный технический университет
Характеристика анализа временных рядов
Методические указания к выполнению лабораторной работы № 4
по дисциплине: Эконометрия
Севастополь, 2000
Анотация
Анализ временных рядов. Методические указания по выполнению лабораторной работы по дисциплине "Эконометрия" / Сост. Букач Б.А. – Севастополь: Изд-во СевГТУ, 2000. – 22 с.
Целью методического указания является обучение студента анализу временных рядов с помощью статистического пакета "Minitab". Методические указания предназначены для студентов экономических специальностей всех форм обучения.
Методические указания содержат описание способов анализа временных данных в статистическом пакете MINITAB.
Содержание
1 Анализ временных рядов
1.1 Анализ тенденции развития (тренда) временного ряда
1.2 Декомпозиция временного ряда. Анализ сезонных колебаний
2 Порядок выполнения работы
3 Варианты заданий к лабораторной работе
4 Контрольные вопросы
Библиография
1 Анализ временных рядов
На практике экономист весьма часто сталкивается с тем, что исходные данные, которыми он располагает для выявления той или иной закономерности, представлены в виде временных (динамических) рядов. Такие ряды описывают изменение некоторой характеристики во времени. Каждый член (уровень) такого ряда связан с соответствующим моментом времени или временным интервалом. Разумеется, уровни ряда должны быть сопоставимыми по своему содержанию. Показатели временных рядов формируются под совокупным влиянием множества длительно и кратковременно действующих факторов и, в том числе, различного рода случайностей. Изменение условий развития явления приводит к более или менее интенсивной смене самих факторов, к изменению силы и результативности их воздействия и, в конечном счете, к вариации уровня изучаемого явления во времени. Лишь в очень редких случаях в экономике встречаются чисто стационарные ряды, т. е. ряды, в которых не наблюдаются систематические изменения в средних значениях уровней, их дисперсиях, и эти характеристики не зависят от начала отсчета времени. В таких случаях вариацию уровней можно изучать с помощью специального раздела математической статистики — теории стационарных процессов. В основном временные ряды, с которыми имеют дело в экономике, не являются стационарными. Последовательность расположения исследуемых данных во времени в таких рядах имеет существенное значение для анализа, т. е. время здесь выступает как один из определяющих для изучаемого явления факторов.
Можно выделить три основные задачи исследования временных рядов.
Первая из них заключается в описании изменения соответствующего показателя во времени и выявлении тех или иных свойств исследуемого ряда. Для этого прибегают к разнообразным способам: расчету обобщающего показателя изменения уровней во времени — среднего темпа роста; применению различных сглаживающих фильтров, уменьшающих колебания уровней во времени и позволяющих более четко представить тенденции развития; подбору кривых, характеризующих эту тенденцию; выделению сезонных и иных периодических и случайных колебаний; измерению зависимости между членами ряда (автокорреляции). К методам описания какого-либо свойства динамики можно с некоторым основанием отнести и методы проверки наличия или отсутствия долговременных тенденций в ряду.
Второй важной задачей анализа является объяснение механизма изменения уровней ряда. Для ее решения обычно прибегают к регрессионному анализу.
Наконец, третья задача ¾ описание изменения временного ряда и объяснение механизма формирования ряда часто используются для статистического прогнозирования, которое в большинстве случаев сводится к экстраполяции обнаруженных тенденций развития.
Анализ временного ряда и последующее прогнозирование его развития может использоваться для:
– планирования в экономике, производстве, торговле;
– управления и оптимизации, протекающих в обществе социально-экономических процессов;
– частичного управления важными параметрами демографических процессов и экологической ниши общества;
– принятия оптимальных решений в бизнесе.
В данной лабораторной работе анализ временного ряда будет производиться в статистическом пакете «MINITAB».
Minitab позволяет анализировать данные, зависящие от времени (временные ряды), выявлять основные закономерности этих зависимостей и на основе полученных моделей прогнозировать будущие значения для этих рядов.
Minitab включает следующие основные виды анализа временных рядов:
Trend Analysis – анализ линии тренда с использованием четырех типов аппроксимирующих кривых (линейная, квадратическая, экспоненциального роста, логистическая S – кривая).
Decomposition – классическая декомпозиция временных рядов.
Moving Average – вычисление скользящего среднего.
Exp Smoothing – экспоненциальное сглаживание временного ряда.
Lag – смещение рядов на заданное значение.
Autocorrelation – вычисление автокорреляционной функции.
Cross Correlation – вычисление кросскорреляционной функции (взаимная корреляция).
ARIMA – оценивание модели Бокса-Дженкинса (autoregressive integrated moving average model) – интегрированная модель авторегрессии и скользящего среднего).
1.1 Анализ тенденции развития (тренда) временного ряда
Понятие тенденция развития не имеет достаточно четкого определения. Обычно тенденцию стремятся представить в виде более или менее гладкой кривой, которой соответствует некоторая функция времени. Эта кривая, назовем ее трендом, характеризует основную закономерность движения во времени и в известной мере (но не полностью) свободна от случайных воздействий. Тренд описывает некоторую усредненную для достаточно протяженного периода наблюдения тенденцию развития во времени. В большинстве случаев полученная траектория связывается исключительно с ходом времени. Предполагается, что с помощью переменной время можно выразить влияние всех основных факторов. Механизм их влияния в явном виде не учитывается.
Для анализа линии тренда в статистическом пакете «MINITAB» необходимо выполнить следующую операцию: Stat > Time Series > Trend Analysis. На мониторе появится следующее диалоговое окно (Рисунок 1.1):
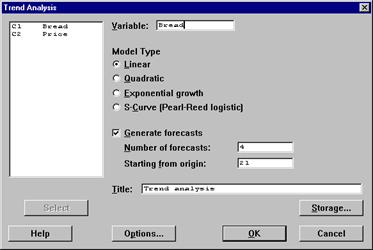
Рисунок 1.1 – Диалоговое окно «Анализ линии тренда»
Диалоговое окно включает в себя следующие параметры:
Variable: вводится идентификатор (название) столбца в таблице с исследуемым временным рядом.
Model Type: определяется тип модели для аппроксимации тренда временного ряда. В используемой программе Minitab рассматриваются следующие четыре типа моделей:
– Linear – линейная;
– Quadratic – квадратическая;
– Exponential growth – экспоненциального роста;
– S-Curve (Pearl-Reed logistic) – логистическая S – кривая.
Generate forecasts: Отмечается при необходимости просчитать прогнозные значения, на графике эти точки отмечаются красным цветом.
Number of forecasts: Вводится число точек для прогноза.
Starting from origin: Вводится положительное число, определяющее с какой точки начинать считать прогнозные значения. Если эта позиция остается не заполненной Minitab начинает считать прогнозные значения, начиная с последней точки исходного временного ряда. Например, если в примере 1 необходимо сделать прогноз валового сбора хлеба на три года вперед, начиная с последнего года, т. е. с 22-го по счету, то в эту позицию вводят число 21 или оставляют незаполненной и программа подсчитает прогноз в точках 22, 23, 24.
Title: Вводится вами заданный заголовок для выводимого графика.
Результат проведенного исследования Minitab выводит в виде графика, на котором показаны исходные данные, аппроксимирующая их линия тренда и рассчитанные прогнозные значения для этого ряда. В качестве оценок точности аппроксимации и вычисленного прогноза Minitab использует следующие три показателя:
MAPE – средняя абсолютная ошибка в процентах (mean absolute percentage error – среднее относительное отклонение);
MAD – среднее абсолютное отклонение (mean absolute deviation);
MSD – s2 – среднеквадратическое отклонение (mean squared deviation). Близко по своей структуре к среднеквадратической ошибке, но не зависит от числа степеней свободы для разных моделей, поэтому может быть использовано для сравнения точности разных моделей.
Вычисляются эти оценки точности следующим образом:
MAPE  , где
, где ![]() ; MAD
; MAD 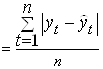 ; MSD
; MSD 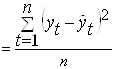 ;
;
Определение типа модели для аппроксимации тренда временного ряда – одна из наиболее сложных задач анализа временных рядов. Оценка коэффициентов уравнения тренда осуществляется по методу наименьших квадратов (МНК).
Наиболее часто в экономике при аппроксимации тренда используются следующие виды функций:
линейная ![]() , параболическая
, параболическая ![]() , степенная
, степенная ![]() ,
,
экспоненциальная ![]() , функция Гомперца
, функция Гомперца ![]() , логистическая
, логистическая
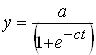 .
.
Пример 1. Рассмотрим динамику валового сбора хлеба и цен на хлеб в России за 1890 –1910 гг., данные представлены в таблице 1.1. Необходимо определить тип модели для аппроксимации имеющихся временных рядов. В качестве критерия оптимальности выбора модели воспользуемся показателем MSD – среднеквадратическим отклонением.
Таблица 1.1
| № | Годы | Валовый сбор хлеба | Цены на хлеб | № | Годы | Валовый сбор хлеба | Цены на хлеб |
| 1. | 1890 | 100 | 100 | 12. | 1901 | 135 | 101 |
| 2. | 1891 | 78 | 131 | 13. | 1902 | 183 | 102 |
| 3. | 1892 | 91 | 148 | 14. | 1903 | 174 | 103 |
| 4. | 1893 | 130 | 114 | 15. | 1904 | 191 | 104 |
| 5. | 1894 | 139 | 89 | 16. | 1905 | 165 | 108 |
| 6. | 1895 | 130 | 84 | 17. | 1906 | 143 | 122 |
| 7. | 1896 | 139 | 85 | 18. | 1907 | 161 | 155 |
| 8. | 1897 | 122 | 83 | 19. | 1908 | 165 | 168 |
| 9. | 1898 | 143 | 108 | 20. | 1909 | 204 | 152 |
| 10. | 1899 | 161 | 109 | 21. | 1910 | 200 | 133 |
| 11. | 1900 | 152 | 102 |
В статистическом пакете Minitab рассматриваются следующие четыре типа моделей: линейная, квадратическая, экспоненциального роста, логистическая S – кривая. Выполним расчеты по каждой из моделей для обоих временных рядов и представим данные расчетов в таблице 2.
Таблица 1.2
| Вид модели | MSD | |
| Валовый сбор хлеба | Цены на хлеб | |
| линейная | 296.219 | 460.058 |
| квадратическая | 272.670 | 258.870 |
| экспоненциального роста | 331.586 | 452.138 |
| логистическая S – кривая | 281.557 | нет данных |
Наиболее точно описывают имеющиеся данные квадратическая модель, так как среднеквадратическое отклонение (MSD) у этой модели наименьшее. Уравнения тренда, описывающие данные временные ряды имеют вид:
– для валового сбора хлеба:
Yt = 84.5263 + 7.88980*t - 0.148474*t2
– для цены на хлеб:
Yt = 130.932 - 7.72938*t + 0.433980*t2
В результате выполнения операции: Stat > Time Series > Trend Analysis и заполнения диалогового окна на экране появятся графики, которые показаны на рисунке 1.2. На графиках видно, что выбранные нами модели тренда достаточно точно описывают имеющиеся временные ряды.
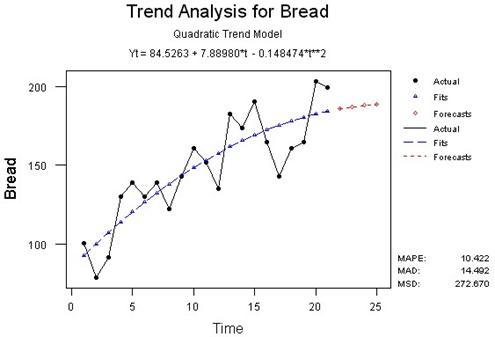
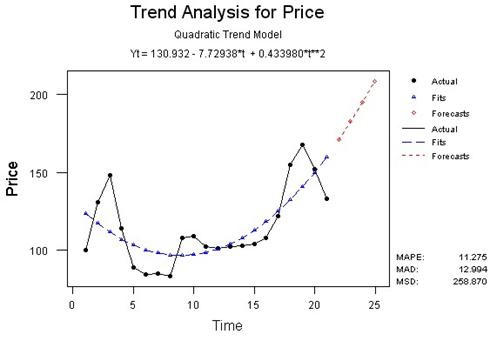
Рисунок 1.2 – Анализ трендов валового сбора хлеба и цены на него
1.2 Декомпозиция временного ряда. Анализ сезонных колебаний
При анализе временного ряда его изменчивость можно разделить на закономерную (детерминированную) и случайную составляющие. Для многих рядов в экономике причины, порождающие их закономерные составляющие не ясны. Тем не менее их совокупное влияние может быть устойчивым в течении достаточно длительных промежутков времени. Это обеспечивает возможность прогноза для подобных временных рядов.
Составная часть временного ряда, остающаяся после выделения из него закономерных (детерминированных) компонент, представляет собой случайную, нерегулярную компоненту. Она является обязательной составной частью любого временного ряда в экономике, так как случайные отклонения неизбежно сопутствуют любому экономическому явлению. Если систематические компоненты временного ряда определены правильно, что как раз и составляет одну из главных целей при разработке моделей временного ряда, то остающаяся после выделения из временного ряда этих компонент так называемая остаточная последовательность (ряд остатков) будет случайной компонентой ряда.
Случайная компонента ряда обладает следующими свойствами:
– случайностью колебаний уровней остаточной последовательности;
– соответствием распределения случайной компоненты нормальному закону распределения;
– равенством математического ожидания случайной компоненты нулю;
– независимостью значений уровней случайной последовательности, то есть отсутствием существенной автокорреляции.
Проверка адекватности моделей временных рядов основана на проверке выполняемости у остаточной последовательности указанных четырех свойств. Если не выполняется хотя бы одно из них, модель признается неадекватной; при выполнении всех четырех свойств модель адекватна. Данная проверка осуществляется с использованием ряда статистических критериев
Закономерную или детерминированную составляющую при анализе экономического временного ряда обычно разбивают на три составляющие: тренд, сезонную компоненту и циклическую компоненту.
Наличие первых двух составляющих временного ряда можно приблизительно определить визуально, построив график временного ряда. На рисунке 1.3 показаны различные виды временных рядов с трендом и сезонной составляющей.
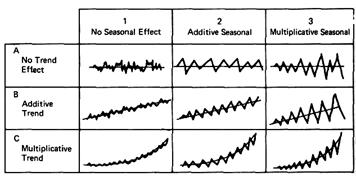
Рисунок 1.3 – Различные виды временных рядов
На рисунке 1.3 введены следующие обозначения:
1 – временной ряд не содержит сезонной составляющей;
2 – временной ряд содержит аддитивную сезонную составляющую;
3 – временной ряд содержит мультипликативную сезонную составляющую;
А – временный ряд не содержит тренда;
В – временной ряд содержит аддитивный тренд;
С – временной ряд содержит мультипликативный тренд (при увеличении данных, увеличивается величина сезонных отклонений).
(Ниже в этом пункте будет рассмотрены понятия аддитивной и мультипликативной переменных временного ряда).
Циклическая компонента временного ряда описывает длительные периоды относительного подъёма и спада. Она состоит из циклов, которые меняются по амплитуде и протяженности. Выделение в экономических временных рядах циклической компоненты связано с тем, что экономическая активность не растет (или спадает) постоянными темпами. Она состоит из периодов относительных подъёмов и спадов. Считается, что причиной циклических изменений в экономических показателях является взаимодействие спроса и предложения. Играют роль и другие факторы: рост и истощение ресурсов, увеличение размеров капитала, используемого в бизнесе, продолжительно действующие неблагоприятные (либо благоприятные) для тех или иных отраслей сельского хозяйства погодные условия, изменения в правительственной финансовой и налоговой политике и т. п. Влияние всех этих факторов приводит к тому, что циклическую компоненту крайне трудно идентифицировать формальными методами, исходя только из данных изучаемого ряда. Поэтому для ее анализа обычно приходиться привлекать дополнительную информацию в виде других временных рядов, которые оказывают влияние на изучаемый ряд, например, учитывать информацию типа налоговых льгот, перенасыщенности рынка и т. п.
В ходе выполнения данной лабораторной работы необходимо будет учитывать влияние лишь двух составляющих: тренда и сезонной компоненты.
К сезонным относятся такие явления, которые обнаруживают в своем развитии определенные закономерности более или менее повторяющиеся из месяца в месяц, из квартала в квартал. Под сезонностью иногда понимают неравномерность производственной деятельности в отраслях промышленности, связанных с переработкой с/х сырья, поступления которого зависит от времени года. Кроме того, сезонность может возникать из-за сезонного характера спроса на товары, производимые промышленностью и т. д. Как бы ни проявлялась сезонность, она наносит большой ущерб народному хозяйству, который заключается в неравномерном использовании оборудования и рабочей силы, неравномерной постановке сырья и загрузке транспорта в отраслях, связанных с сезонным производством. Изучение сезонных колебаний необходимо для более ритмичной работы предприятий.
Статистическое исследование сезонности ставит следующие задачи: численно выразить проявление сезонных колебаний; выявить их силу и характер в условиях отдельных отраслей народного хозяйства; вскрыть факторы, вызывающие сезонные колебания; найти экономические последствия проявления сезонности. Известно несколько способов исследования сезонных колебаний: способ простых средних, способ относительных чисел, способ Персонса, способ расчета сезонных волн, базирующийся на определении тенденции (методом скользящей средней и методом наименьших квадратов).
Индексы сезонности являются показателями, характеризующими результаты сравнения фактических уровней данного месяца или квартала с уровнями, вычисленными при выявлении основной тенденции для того же месяца или квартала.
Расчет сезонного индекса может быть произведен
следующим образом. Предположим, что рассматриваемый временной ряд x1, … xn может быть описан аддитивной моделью. Пусть p – период последовательности
st. Для этого сначала мы должны оценить
тренд ![]() . Затем
для каждого сезона i, 1
. Затем
для каждого сезона i, 1 ![]() i
i ![]() p, необходимо рассмотреть все относящиеся к нему разности: xi –
p, необходимо рассмотреть все относящиеся к нему разности: xi – ![]() . Каждое из этих отклонений xi от
. Каждое из этих отклонений xi от ![]() можно рассматривать как результат влияния
сезонных изменений. Усреднение этих разностей дает нам оценку сезонной компоненты
si. В качестве простейшей оценки можно взять
простое среднее, т.е.:
можно рассматривать как результат влияния
сезонных изменений. Усреднение этих разностей дает нам оценку сезонной компоненты
si. В качестве простейшей оценки можно взять
простое среднее, т.е.:
![]() для i = 1,…, p
для i = 1,…, p
Сезонный индекс для мультипликативной модели вычисляется по другой формуле.
Minitab производит классическую декомпозицию временного ряда, используя мультипликативную или аддитивную модели. С помощью этой процедуры временной ряд разделяется на три составляющие: тренд, сезонные колебания и ошибку.
Для работы с этим видом анализа необходимо набрать: Stat > Time Series > Decomposition. В результате выполнения этой процедуры на мониторе появится следующие диалоговое окно (рисунок 1.4).
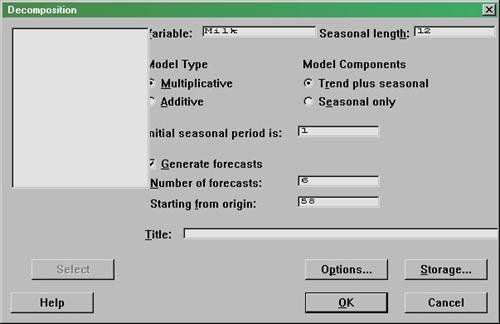
Рисунок 1.4 – Вид диалогового окна "Анализ сезонной декомпозиции"
Диалоговое окно включает в себя следующие параметры:
Variable: выбирается столбец, содержащий исходный временной ряд.
Seasonal Length: Длина сезонного цикла. Вводится целое число большее 2.
Model Type: Выбирается тип модели:
– мультипликативная модель. Используется, если сезонные колебания зависят от уровня данных. В этом случае предполагается, что если данные увеличиваются, то увеличивается и величина сезонных отклонений. Многие временные ряды соответствуют этой модели. Модель имеет следующий вид
yt = Trend * Seasonal * Error
– аддитивная модель имеет следующий вид:
yt = Trend + Seasonal + Error
Model Components: Выбор компонентов присутствующих в модели:
– Trend plus seasonal: Отмечается, если исходные данные содержат тренд и сезонную составляющую.
– Seasonal only: Отмечается, если при анализе тренд не учитывается. Если данные содержат тренд, но это не указано, то оценки сезонных индексов могут быть не верными.
Initial seasonal period: По умолчанию Minitab считает, что исходные данные начинаются с первого периода – 1. Если исследуются месячные данные, и они начинаются с июня, то тогда указывается 6 месяц.
Generate forecasts: Отмечается, если необходимо сделать прогноз. Прогнозные значения отмечаются на графике красным цветом.
Number of forecasts: Вводится число прогнозных значений.
Starting from origin: Используется аналогично диалогу в анализе тренда.
Title: Можно ввести свое название графика.
Minitab при декомпозиции:
- оценивает линию тренда методом наименьших квадратов;
- удаляет тренд, деля на тренд или вычитая его из временного ряда в зависимости от используемой модели (соответственно мультипликативной или аддитивной);
- сглаживает преобразованные данные, используя метод скользящего среднего с параметром сглаживания равным длине сезонного цикла. Если сезонный цикл четный, то используется двухшаговая процедура сглаживания методом скользящего среднего;
- временной ряд без тренда делится или из него вычитается полученный сглаженный ряд, чтобы получить сезонную компоненту. С помощью полученных значений вычисляются сезонные индексы, которые позволяют оценить влияние сезонных колебаний.
Рассмотрим на примере производства молока процедуру декомпозиции временного ряда (данные представлены в таблице 1.2).
Таблица 1.2 – Производство молока в России за 1992–1996 гг. (тыс. тонн в месяц)
|
Месяц \ год |
1992 г. |
1993 г. |
1994 г. |
1995 г. |
1996 г. |
|
январь |
2015 | 1759 | 1510 | 1172 | 1038 |
|
февраль |
2123 | 1773 | 1484 | 1226 | 1104 |
|
март |
2624 | 2361 | 1988 | 1651 | 1439 |
|
апрель |
2891 | 2649 | 2211 | 1859 | 1521 |
|
май |
3335 | 3203 | 2559 | 2392 | 1827 |
|
июнь |
4071 | 3936 | 3209 | 2864 | 2446 |
|
июль |
4040 | 3861 | 3204 | 2714 | 2369 |
|
август |
3392 | 3321 | 2687 | 2420 | 2081 |
|
сентябрь |
2467 | 2438 | 2031 | 1925 | 1577 |
|
октябрь |
2092 | 1760 | 1506 | 1338 | 1081 |
|
ноябрь |
1494 | 1299 | 1050 | 984 | |
|
декабрь |
1562 | 1345 | 1054 | 1020 |
Заполним диалоговое окно, изображенное на рисунке 1.4, следующим образом:
Variable: 1992–96
Seasonal Length: 12
Model Type: мультипликативная модель (для выбора типа модели можно использовать рисунок 1.3. Из графика анализирующего временной ряд на наличие тренда (рисунок 1.5) видно, что величина сезонных колебаний пропорциональна среднему уровню производства. Поэтому для описания сезонных колебаний следует использовать мультипликативную модель).
Model Components: Trend plus seasonal (тренд и сезонная составляющая)
Initial seasonal period: 1 (данные начинаются с января)
Generate forecasts:
Number of forecasts: 6
В результате выполнения этой операции на экране появятся следующие графики и расчеты. В окне Session появятся результаты вычисления сезонных индексов и значения прогнозных показателей на полгода вперед, а также уравнение тренда и его точность:
Time Series Decomposition (Декомпозиция временного ряда)
Data 1992-96 (Название анализируемых данных)
Length 58.0000 (Длина временного ряда)
NMissing 0 (Количество ошибок в данных)
Trend Line Equation (Уравнение тренда)
Yt = 2841.10 - 23.6304*t
Seasonal Indices (Сезонные индексы)
| Period | Index |
| 1 | 0.654509 |
| 2 | 0.678928 |
| 3 | 0.909029 |
| 4 | 1.02617 |
| 5 | 1.27273 |
| 6 | 1.58137 |
| 7 | 1.54385 |
| 8 | 1.35862 |
| 9 | 1.02653 |
| 10 | 0.777468 |
| 11 | 0.570636 |
| 12 | 0.600173 |
Accuracy of Model (Оценка точности полученного уравнения тренда)
MAPE: 4.1
MAD: 85.0
MSD: 10808.6
Forecasts (Прогнозные значения)
| Row | Period | Forecast |
| 1 | 59 | 826.68 |
| 2 | 60 | 855.31 |
| 3 | 61 | 917.31 |
| 4 | 62 | 935.52 |
| 5 | 63 | 1231.15 |
| 6 | 64 | 1365.59 |
При проведении декомпозиции Minitab также генерирует три набора графиков (рисунки 1.5 – 1.7).
На рисунке 1.5 изображены исходные данные, оцененная линия тренда, оцененная линия тренда с сезонными колебаниями (predicted) и прогнозные значения.
На рисунке 1.6 изображены отдельные графики для каждой компоненты: исходные данные, данные без тренда, данные без сезонных колебаний и график ошибки – данные без тренда и без сезонных колебаний.
Эта группа графиков показывает как сезонные колебания влияют на временной ряд. Сюда входят графики:
- сезонных индексов (Seasonal Indices),
- график процента дисперсии обусловленной сезонными колебаниями (Percent Variation, by Seasonal Period),
- график разброса исходных данных за рассматриваемый сезонный период (Original Data, by Seasonal Period),
- график разброса остатков за этот период (Residuals, by Seasonal Period).
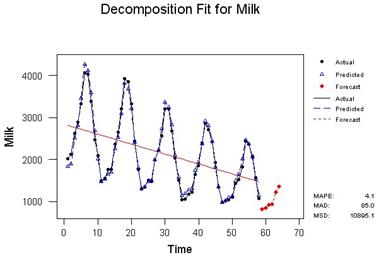
Рисунок 1.5 – График временного ряда
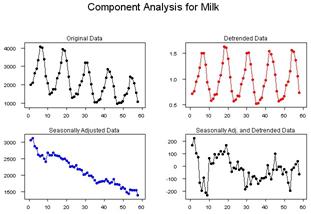
Рисунок 1.6 – Результаты компонентного анализа при декомпозиции временного ряда.
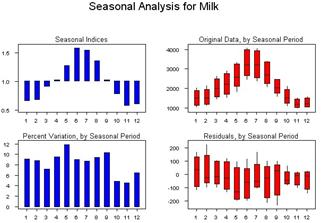
Рисунок 1.7 – Результаты сезонного анализа при декомпозиции временного ряда
В результате проведенного анализа можно сделать следующие выводы:
1. Визуальный анализ графика ряда показывает, что производство молока имеет тенденцию к сокращению. Это может быть обусловлено сокращением поголовья молочного стада и общим снижением производства сельскохозяйственной продукции.
2. Временный ряд подвержен сильным сезонным колебаниям с максимумом производства в летние месяцы (апрель – сентябрь) и минимумом – в зимние (октябрь – март). При этом величина сезонных колебаний пропорциональна среднему уровню производства.
Следовательно, потребителю молочных продуктов необходимо быть готовым к сезонным изменениям уровня цен на продукцию: в летние месяцы — снижение цены, в зимние — возрастание.
2 Порядок выполнения работы
1 В соответствии с вариантом задания создать таблицу исходных данных. 2 Выполнить процедуру анализа временного ряда:
– определить уравнение тренда, который наиболее точно описывает данный временной ряд;
– провести полную декомпозицию временного ряда, определить сезонные индексы;
– сделать прогноз на полгода вперед.
3 Переписать все полученные данные в отчет.
4 Сделать выводы об исследуемом временном ряде.
3 Варианты заданий к лабораторной работе
Вариант № 1 Поквартальные индексы розничной цены на овощи в Великобритании (1951 – 1958 гг.) в фунтах.
|
|
1951 |
1952 |
1953 |
1954 |
1955 |
1956 |
1957 |
1958 |
|
1 квартал |
295,0 | 324,7 | 372,9 | 354,0 | 333,7 | 323,2 | 304,3 | 312,5 |
|
2 квартал |
317,5 | 323,7 | 380,9 | 345,7 | 323,9 | 342,9 | 285,9 | 336,1 |
|
3 квартал |
314,9 | 322,5 | 353,0 | 319,5 | 312,8 | 300,3 | 292,3 | 295,5 |
|
4 квартал |
321,4 | 332,9 | 348,9 | 317,6 | 310,2 | 309,8 | 298,7 | 318,4 |
Вариант № 2 Помесячная продажа пива в Австралии (1991 – 1995 гг.) млн. л.
|
Месяц |
1991 |
1992 |
1993 |
1994 |
1995 |
|
Январь |
164 |
147 |
139 |
151 |
138 |
|
Февраль |
148 |
133 |
143 |
134 |
136 |
|
Март |
152 |
163 |
150 |
164 |
152 |
|
Апрель |
144 |
150 |
154 |
126 |
127 |
|
Май |
155 |
129 |
137 |
131 |
151 |
|
Июнь |
125 |
131 |
129 |
125 |
130 |
|
Июль |
153 |
145 |
128 |
127 |
119 |
|
Август |
146 |
137 |
140 |
143 |
153 |
|
Сентябрь |
138 |
138 |
143 |
143 |
|
|
Октябрь |
190 |
168 |
151 |
160 |
|
|
Ноябрь |
192 |
176 |
177 |
190 |
|
|
Декабрь |
192 |
188 |
184 |
182 |
|
Вариант № 3 Данные ежемесячного объёма реализации товара А (в тыс. грн.). После выполнения процедуры декомпозиции временного ряда, предложите свои варианты, чем может в действительности являться товар А.
|
Месяц |
1995 |
1996 |
1997 |
1998 |
1999 |
|
Январь |
742 |
741 |
896 |
951 |
1030 |
|
Февраль |
697 |
700 |
793 |
861 |
1032 |
|
Март |
776 |
774 |
885 |
938 |
1126 |
|
Апрель |
898 |
932 |
1055 |
1109 |
1285 |
|
Май |
1030 |
1099 |
1204 |
1274 |
1468 |
|
Июнь |
1107 |
1223 |
1326 |
1422 |
1637 |
|
Июль |
1165 |
1290 |
1303 |
1486 |
1611 |
|
Август |
1216 |
1349 |
1436 |
1555 |
1608 |
|
Сентябрь |
1208 |
1341 |
1473 |
1604 |
1528 |
|
Октябрь |
1131 |
1296 |
1453 |
1600 |
1420 |
|
Ноябрь |
971 |
1066 |
1170 |
1403 |
1119 |
|
Декабрь |
783 |
901 |
1023 |
1209 |
1013 |
Вариант № 4 Количество пассажиров, перевезенных авиа компанией "PanAmerican", в месяц (в тыс.)
|
Месяц |
1969 |
1970 |
1971 |
1972 |
|
Январь |
112 |
115 |
145 |
171 |
|
Февраль |
118 |
126 |
150 |
180 |
|
Март |
132 |
141 |
178 |
193 |
|
Апрель |
129 |
135 |
163 |
181 |
|
Май |
121 |
125 |
172 |
183 |
|
Июнь |
135 |
149 |
178 |
218 |
|
Июль |
148 |
170 |
199 |
230 |
|
Август |
148 |
170 |
199 |
242 |
|
Сентябрь |
136 |
158 |
184 |
209 |
|
Октябрь |
119 |
133 |
162 |
191 |
|
Ноябрь |
104 |
114 |
146 |
172 |
|
Декабрь |
118 |
140 |
166 |
194 |
Вариант № 5 Данные ежемесячного реализации товара В. После выполнения процедуры декомпозиции временного ряда, предложите свои варианты, чем может в действительности являться товар В.
|
Месяц |
1991 |
1992 |
1993 |
1994 |
1995 |
|
Январь |
53,5 |
52,1 |
52,3 |
53,3 |
54,8 |
|
Февраль |
53,0 |
51,5 |
51,5 |
53,1 |
54,2 |
|
Март |
53,2 |
51,5 |
51,7 |
53,5 |
54,6 |
|
Апрель |
52,5 |
52,4 |
51,5 |
53,5 |
54,3 |
|
Май |
53,4 |
53,3 |
52,5 |
53,9 |
54,8 |
|
Июнь |
56,5 |
55,5 |
57,1 |
57,1 |
58,1 |
|
Июль |
65,3 |
64,2 |
63,6 |
6,7 |
68,1 |
|
Август |
70,7 |
69,6 |
68,6 |
69,4 |
73,3 |
|
Сентябрь |
66,9 |
69,3 |
68,9 |
70,3 |
75,5 |
|
Октябрь |
58,2 |
58,5 |
60,1 |
62,6 |
66,4 |
|
Ноябрь |
55,3 |
55,3 |
55,6 |
57,9 |
60,5 |
|
Декабрь |
53,4 |
53,6 |
53,9 |
55,8 |
57,7 |
Вариант № 6 Дан ежемесячный объём реализации товаров торгового предприятия (в тыс. грн.). После выполнения процедуры декомпозиции временного ряда, предложите свои варианты, какие виды товаров может реализовывать предприятие.
|
Месяц |
1995 |
1996 |
1997 |
1998 |
1999 |
|
Январь |
322 |
322 |
330 |
348 |
361 |
|
Февраль |
317 |
318 |
326 |
345 |
354 |
|
Март |
319 |
320 |
329 |
349 |
357 |
|
Апрель |
323 |
326 |
337 |
355 |
367 |
|
Май |
327 |
332 |
345 |
362 |
376 |
|
Июнь |
328 |
334 |
350 |
367 |
381 |
|
Июль |
325 |
335 |
351 |
366 |
381 |
|
Август |
326 |
336 |
354 |
370 |
383 |
|
Сентябрь |
330 |
335 |
355 |
371 |
384 |
|
Октябрь |
334 |
338 |
357 |
375 |
387 |
|
Ноябрь |
337 |
342 |
362 |
380 |
392 |
|
Декабрь |
341 |
348 |
366 |
385 |
396 |
4 Контрольные вопросы
1. Какие три основные задачи анализа временных рядов?
2. Где используются в экономике результаты анализа временных рядов?
3. Какие основные математические функции используются при аппроксимации временных рядов в экономике?
4. Какой критерий в данной работе используется для сравнения точности моделей?
5. На какие составляющие разбивается временной ряд при его декомпозиции?
6. Какие факторы в экономике влияют на наличие сезонной и циклической составляющей временного ряда?
7. Какие типы моделей используются при декомпозиции временного ряда?
8. Какими свойствами должна обладать случайная составляющая?
Библиография
1 Г.С. Кильдышев, А.А. Френкель. Анализ временных рядов и прогнозирование. — М.: Статистика. 1973 — 101 с.
2 М. Кендалл, А. Стьюарт. Многомерный статистический анализ и временные ряды. — М.: Наука, 1976. — 736 с.
3 Ю.Н. Тюрин, А.А. Макаров. Статистический анализ данных на компьютере / Под ред. В.Э. Фигурнова — М.: ИНФРА–М, 1998. — 528 с.
4 Makridakis S. Forecasting: methods and applications. / Makridakis S., Wheelwright S, Hyndman R. — New York: John Wiley & Sons, Inc., 1998. — 642 c.
| Внутридневная торговля на рынке Forex | |
|
Внутридневная торговля на рынке FOREX СОДЕРЖАНИЕ Введение . 7 Необходимое оборудование . 7 Часть первая. Анализ . 11 Введение в суть технического ... Малый тренд (обычно длится менее месяца) имеет наименьшее значение из трех и измеряет краткосрочные колебания рынка. срочного тренда Трейдеры, которые специализируются на рынках фьючерсов и играют на коротких (сленг), любят применять 40-дневную среднюю 20-дневная средняя также используется в ... |
Раздел: Рефераты по банковскому делу Тип: дипломная работа |
| Применение программного комплекса Electronics Workbench для разработки ... | |
|
Аннотация В дипломной работе рассматривается анализ радиоэлектронных схем, а также возможность их моделирования современными компьютерными методами, а ... Если мгновенные ток и напряжение АЭ соответствуют участку отрицательной крутизны динамической ВАХ, то колебания первых гармоник ia(t) и ua(t) противофазны, поэтому на частоте ... При выполнении команды открывается диалоговое окно Circuit/Component Properties, закладки которого зависят от типа выбранного компонента. |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Анализ структуры цен на фондовом рынке | |
|
Министерство образования и науки Украины НАЦИОНАЛЬНЫЙ ГОРНЫЙ УНИВЕРСТИТЕТ ИНСТИТУТ ЭКОНОМИКИ Факультет менеджмента Кафедра экономической кибернетики и ... На графике можно увидеть пересечение тренда цены и СС на 53 день, но данный сигнал не может быть подтверждением предыдущего, т.к. пресечение происходит после флета. Активизировать компоненту Рисунок 1, где раньше заданным диапазонам строится график. |
Раздел: Рефераты по банковскому делу Тип: дипломная работа |
| Управление оборотными активами предприятия ОАО "Хлеб" | |
|
Введение Эффективное управление оборотными активами играет большую роль в обеспечении нормальной работы предприятия, повышении уровня рентабельности ... постоянная часть оборотных активов, которая представляет собой неизменную часть их размера, которая не зависит от сезонных и других колебаний операционной деятельности предприятия ... - свести прогнозные варианты плана поступления и расходования денежных средств к одному реальному заданию по формированию денежных потоков предприятия в рамках одного месяца; |
Раздел: Рефераты по финансовым наукам Тип: дипломная работа |
| Математические модели в менеджменте и маркетинге | |
|
КОНСПЕКТ по дисциплине "Математические модели в менеджменте и маркетинге" 1. МЕТОДЫ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ В реальных системах управления ... Метод скользящего среднего, изложенный ниже, можно использовать для выделения тренда из модели, содержащей сезонную компоненту. Временной ряд может состоять из собственно тренда - общей тенденции изменения значений переменной; сезонной вариации - краткосрочных периодических колебаний значений переменной ... |
Раздел: Рефераты по экономико-математическому моделированию Тип: учебное пособие |