Курсовая работа: Эконометрическое моделирование
Министерство образования и науки Украины
Таврический национальный университет им. В.И. Вернадского
Судакский факультет управления и экономики
Кафедра информационного менеджмента
Курсовая работа по курсу
"Эконометрия"
Выполнила:
студент гр. 31- МО
Абибуллаев ВВ.
Проверил:
Ст. преподователь
Заболотский А. С.
Судак, 2011 г
Этап №1. Эконометрическое моделирование
1 шаг. Пояснение экономического содержания показателей.
Наименование показателей:
1. Розничный товарооборот государственной и кооперативной торговли на душу населения
2. Среднемесячная денежная заработная плата рабочих и служащих
3. Средний размер вклада в сберегательном банке
4. Доля жителей в трудоспособном возрасте
5. Продажа алкогольных напитков на душу населения
Доля жителей в трудоспособном возрасте – это естественно-искусственный показатель, который влияет на среднемесячную денежную заработную плату рабочих и служащих.
Среднемесячная денежная заработная плата рабочих и служащих - это искусственный показатель, который складывается под влиянием доли жителей в трудоспособном возрасте и влияет на средний размер вклада в сберегательном банке и продажу алкогольных напитков на душу населения.
Средний размер вклада в сберегательном банке и продажа алкогольных напитков на душу населения, в свою очередь, влияют на розничный товарооборот государственной и кооперативно торговли на душу населения.
2шаг. Причинно-следственный анализ показателей и соподчинение их в иерархию:
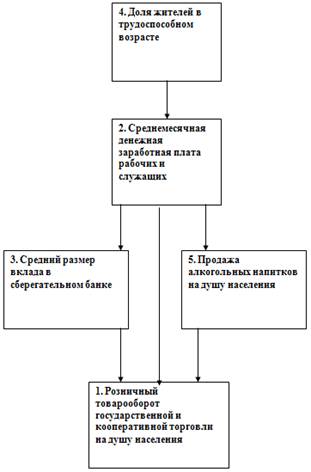
![]()
3 шаг. Статистическая характеристика выборочной совокупности по регионам (средняя, средняя геометрическая, мода, медиана, среднее геометрическое отклонение, коэффициент вариации, асимметрия, эксцесс)
Таблица №1 Перечень показателей
| № | Области | 1 | 2 | 3 | 4 | 5 |
| 1 | Республика Крым | 2861 | 464,4 | 2136 | 58 | 4,9 |
| 2 | Винницкая | 2102 | 407,8 | 2122 | 52,6 | 2,5 |
| 3 | Волынская | 2224 | 426,3 | 2166 | 52,7 | 3,3 |
| 4 | Днепропетровская | 2386 | 508,2 | 2040 | 57,2 | 3,9 |
| 5 | Донецкая | 2671 | 547,7 | 2118 | 56,7 | 4,9 |
| 6 | Житомирская | 2230 | 474,1 | 2219 | 52,9 | 3,1 |
| 7 | Закарпатская | 2457 | 387,5 | 2373 | 56 | 5,5 |
| 8 | Запорожская | 2733 | 500,3 | 2110 | 57,1 | 4,5 |
| 9 | Ивано-Франковская | 2140 | 429,4 | 1954 | 54,4 | 4 |
| 10 | Киевская | 2093 | 493,5 | 2237 | 54,9 | 2,5 |
| 11 | Кировоградская | 2121 | 448 | 2184 | 53,8 | 3,2 |
| 12 | Луганская | 2475 | 516,3 | 2020 | 56,4 | 4,5 |
| 13 | Львовская | 2553 | 443,5 | 2185 | 56,1 | 4,8 |
| 14 | Николаевская | 2608 | 439,9 | 2191 | 56,3 | 3,3 |
| 15 | Одесская | 2576 | 445,2 | 2464 | 57,4 | 4,1 |
| 16 | Полтавская | 2290 | 470,8 | 2257 | 53,6 | 4,2 |
| 17 | Ровенская | 2248 | 444,2 | 1951 | 53,7 | 3 |
| 18 | Сумская | 2154 | 471,1 | 2323 | 53,2 | 3,7 |
| 19 | Тернопольская | 2078 | 417,1 | 2071 | 52,5 | 3,2 |
| 20 | Харьковская | 2590 | 463,7 | 2146 | 56,9 | 4,7 |
| 21 | Херсонская | 2546 | 443,7 | 2048 | 57 | 4,5 |
| 22 | Хмельницкая | 2109 | 435,8 | 2067 | 52,7 | 2,2 |
| 23 | Черкасская | 2398 | 461,7 | 2254 | 53,2 | 3,4 |
| 24 | Черновецкая | 2242 | 392,9 | 18,63 | 54,5 | 3 |
| 25 | Черниговская | 2209 | 419,8 | 2484 | 51,1 | 4,4 |
Таблица №2 Расчет параметров по показателям
| Показатели | 1 | 2 | 3 | 4 | 5 |
| Среднее | 2363,76 | 454,116 | 2085,545 | 54,836 | 3,812 |
| Стандартная ошибка | 45,86314 | 7,712748 | 90,38595 | 0,396017 | 0,174864 |
| Медиана | 2290 | 445,2 | 2146 | 54,5 | 3,9 |
| Мода | #Н/Д | #Н/Д | #Н/Д | 52,7 | 4,5 |
| Стандартное отклонение | 229,3157 | 38,56374 | 451,9297 | 1,980084 | 0,874319 |
| Дисперсия выборки | 52585,69 | 1487,162 | 204240,5 | 3,920733 | 0,764433 |
| Эксцесс | -0,89828 | 0,221876 | 20,07951 | -1,35075 | -0,88971 |
| Асимметричность | 0,481048 | 0,49941 | -4,24965 | -0,03999 | -0,04171 |
| Интервал | 783 | 160,2 | 2465,37 | 6,9 | 3,3 |
| Минимум | 2078 | 387,5 | 18,63 | 51,1 | 2,2 |
| Максимум | 2861 | 547,7 | 2484 | 58 | 5,5 |
| Сумма | 59094 | 11352,9 | 52138,63 | 1370,9 | 95,3 |
| Счет | 25 | 25 | 25 | 25 | 25 |
| Уровень надежности(95,0%) | 94,65685 | 15,91833 | 186,5474 | 0,817338 | 0,360901 |
4 шаг. Геометрическая иллюстрация статистических наблюдений
1-ый показатель
| Карман | Частота | P=m/n | Кумулята |
| 2100 | 2 | 0,08 | 0,08 |
| 2200 | 5 | 0,2 | 0,28 |
| 2300 | 6 | 0,24 | 0,52 |
| 2400 | 2 | 0,08 | 0,6 |
| 2500 | 2 | 0,08 | 0,68 |
| 2600 | 4 | 0,16 | 0,84 |
| 2700 | 2 | 0,08 | 0,92 |
| 2800 | 1 | 0,04 | 0,96 |
| 2900 | 1 | 0,04 | 1 |
| Еще | 0 | 0 |
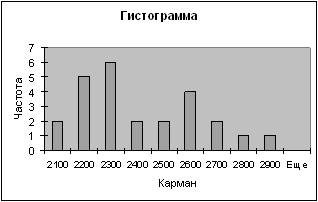
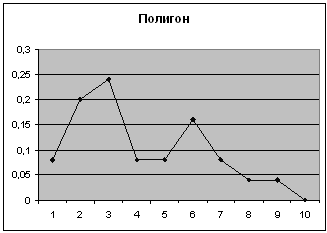
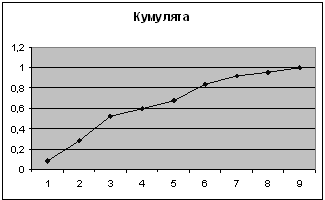
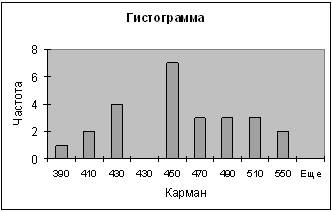
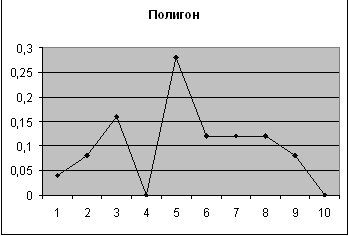
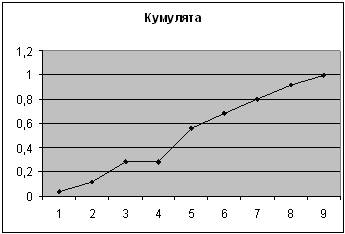
2-ой показатель
| Карман | Частота | P=m/n | Кумулята |
| 390 | 1 | 0,04 | 0,04 |
| 410 | 2 | 0,08 | 0,12 |
| 430 | 4 | 0,16 | 0,28 |
| 430 | 0 | 0 | 0,28 |
| 450 | 7 | 0,28 | 0,56 |
| 470 | 3 | 0,12 | 0,68 |
| 490 | 3 | 0,12 | 0,8 |
| 510 | 3 | 0,12 | 0,92 |
| 550 | 2 | 0,08 | 1 |
| Еще | 0 | 0 |
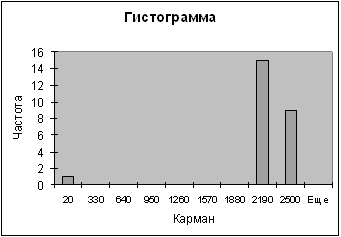
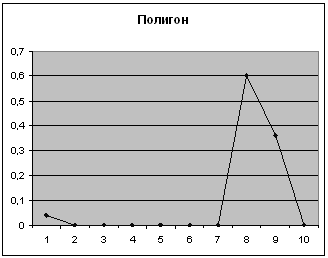
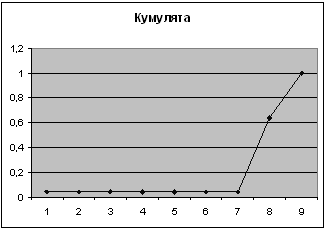
3-ий показатель
| Карман | Частота | P=m/n | Кумулята |
| 20 | 1 | 0,04 | 0,04 |
| 330 | 0 | 0 | 0,04 |
| 640 | 0 | 0 | 0,04 |
| 950 | 0 | 0 | 0,04 |
| 1260 | 0 | 0 | 0,04 |
| 1570 | 0 | 0 | 0,04 |
| 1880 | 0 | 0 | 0,04 |
| 2190 | 15 | 0,6 | 0,64 |
| 2500 | 9 | 0,36 | 1 |
| Еще | 0 | 0 |
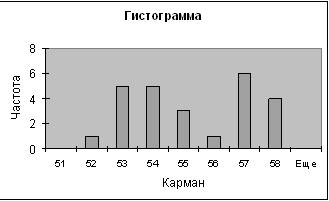
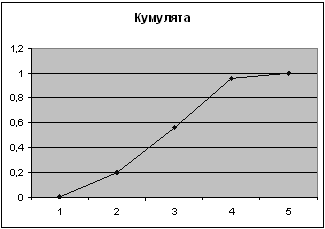
4-ый показатель
| Карман | Частота | P=m/n | Кумулята |
| 51 | 0 | 0 | 0 |
| 52 | 1 | 0,04 | 0,04 |
| 53 | 5 | 0,2 | 0,24 |
| 54 | 5 | 0,2 | 0,44 |
| 55 | 3 | 0,12 | 0,56 |
| 56 | 1 | 0,04 | 0,6 |
| 57 | 6 | 0,24 | 0,84 |
| 58 | 4 | 0,16 | 1 |
| Еще | 0 | 0 |
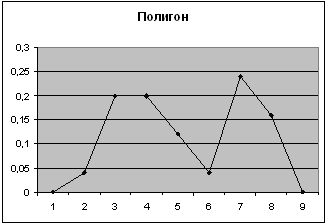
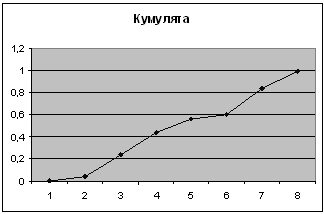
5-ый показатель
| Карман | Частота | P=m/n | Кумулята |
| 2 | 0 | 0 | 0 |
| 3 | 5 | 0,2 | 0,2 |
| 4 | 9 | 0,36 | 0,56 |
| 5 | 10 | 0,4 | 0,96 |
| 6 | 1 | 0,04 | 1 |
| Еще | 0 | 0 |


Этап №2. Однофакторная регрессия
1 шаг. Сравнение 1-го со 2-м:
Моделирование экономических процессов с помощью математических зависимостей заключается в подборе вида функции, которая гипотетически описывает эти процессы.
В нашем случае в качестве такой функции выбираем линейную зависимость между факторами.
Для этого введем следующие показатели:
Y – розничный товарооборот государственной и кооперативной торговли на душу населения
Х – среднемесячная денежная заработная плата рабочих и служащих
Тогда зависимость между ними будет характеризоваться следующим уравнением:
![]()
На основе данных, указанных в таблице 1, рассчитаем параметры модели, оценив ее статистическую надежность и адекватность реальным условиям.
2 шаг. Оценка параметров модели с помощью метода наименьших квадратов
Параметры модели нужно оценить по методу наименьших квадратов, т.к. он обеспечивает минимальную дисперсию опытных данных и в случае линейных зависимостей является наилучшим.
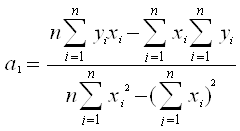
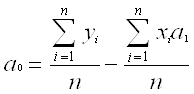
3 шаг. Оценка значимости рассчитанных параметров
Оценка параметров модели по данным формулам при помощи электронных таблиц Excel дает следующий результат:
а0=45,06
а1=0,02
Следовательно, уравнение связи между факторами имеет следующий вид:
У=45,06+0,02Х1
4 шаг. Тестирование модели.
Рассчитаем коэффициент линейной корреляции.
Коэффициент адекватности модели рассчитываем при помощи электронных таблиц Excel, используя надстройку. Анализ данных и получаем следующие значения:
Таблица №3
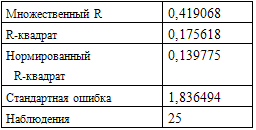
Определение коэффициента детерминации. Он показывает изменение результирующего признака под действием факторного.
Таким образом, действием фактора среднемесячной денежной заработной платы рабочих и служащих можно объяснить лишь 17,5% изменения результирующего признака - розничный товарооборот государственной и кооперативной торговли на душу населения.
Вывод: анализ данной однофакторной модели показал, что она имеет низкую описательную силу. Выявлено наличие слабой связи между показателями среднемесячной денежной заработной платой рабочих и служащих и розничным товарооборотом государственной и кооперативной торговли на душу населения.
5 шаг.
| Наблюдение | Предсказанное Y | Остатки |
| 1 | 55,05728 | 2,942715 |
| 2 | 53,8394 | -1,2394 |
| 3 | 54,23747 | -1,53747 |
| 4 | 55,99975 | 1,200255 |
| 5 | 56,84968 | -0,14968 |
| 6 | 55,266 | -2,366 |
| 7 | 53,4026 | 2,597401 |
| 8 | 55,82976 | 1,270242 |
| 9 | 54,30418 | 0,095823 |
| 10 | 55,68344 | -0,78344 |
| 11 | 54,7044 | -0,9044 |
| 12 | 56,17404 | 0,225964 |
| 13 | 54,60757 | 1,492428 |
| 14 | 54,53011 | 1,769891 |
| 15 | 54,64415 | 2,755849 |
| 16 | 55,195 | -1,595 |
| 17 | 54,62263 | -0,92263 |
| 18 | 55,20145 | -2,00145 |
| 19 | 54,03951 | -1,53951 |
| 20 | 55,04222 | 1,857778 |
| 21 | 54,61188 | 2,388125 |
| 22 | 54,44189 | -1,74189 |
| 23 | 54,99919 | -1,79919 |
| 24 | 53,51879 | 0,981207 |
| 25 | 54,09761 | -2,99761 |
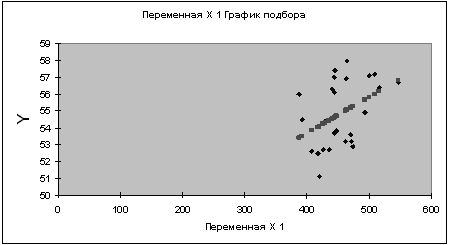
Вывод: в результате анализа однофакторной эконометрической модели, характеризующей взаимосвязь между долей жителей в трудоспособном возрасте и среднемесячной денежной заработной платой рабочих и служащих, можно отметить, что модель имеет высокую описательную силу. Выявлена довольно значительная связь между этими показателями.
Этап №3. Множественная линейная эконометрическая модель
Для сложных систем характерно большое число входных параметров, влияющих на их состояние. Экономические явления представляют собой многофакторные системы, в которых состояние результирующего признака зависит от целой группы таких параметров. Поэтому для изучения процессов в экономике следует применять методы многофакторного анализа. В данном разделе работы проводится пример построения двухфакторной модели, как простейшего случая многофакторных систем.
Y - розничный товарооборот государственной и кооперативной торговли на душу населения
X1 - продажа алкогольных напитков на душу населения
Х2 – среднемесячная денежная заработная плата рабочих и служащих
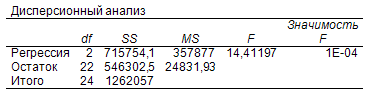
Расчетные данные указаны в таблице:
| Y | X1 | X2 |
| 2861 | 4,9 | 464,4 |
| 2102 | 2,5 | 407,8 |
| 2224 | 3,3 | 426,3 |
| 2386 | 3,9 | 508,2 |
| 2671 | 4,9 | 547,7 |
| 2230 | 3,1 | 474,1 |
| 2457 | 5,5 | 387,5 |
| 2733 | 4,5 | 500,3 |
| 2140 | 4 | 429,4 |
| 2093 | 2,5 | 493,5 |
| 2121 | 3,2 | 448 |
| 2475 | 4,5 | 516,3 |
| 2553 | 4,8 | 443,5 |
| 2608 | 3,3 | 439,9 |
| 2576 | 4,1 | 445,2 |
| 2290 | 4,2 | 470,8 |
| 2248 | 3 | 444,2 |
| 2154 | 3,7 | 471,1 |
| 2078 | 3,2 | 417,1 |
| 2590 | 4,7 | 463,7 |
| 2546 | 4,5 | 443,7 |
| 2109 | 2,2 | 435,8 |
| 2398 | 3,4 | 461,7 |
| 2242 | 3 | 392,9 |
| 2209 | 4,4 | 419,8 |

| Наблюдение | Предсказанное Y | Остатки |
| 1 | 2568,515 | 292,4853 |
| 2 | 2069,892 | 32,10848 |
| 3 | 2235,592 | -11,5916 |
| 4 | 2454,054 | -68,0542 |
| 5 | 2683,852 | -12,8521 |
| 6 | 2266,754 | -36,7543 |
| 7 | 2567,102 | -110,102 |
| 8 | 2548,179 | 184,8205 |
| 9 | 2362,458 | -222,458 |
| 10 | 2188,552 | -95,5519 |
| 11 | 2248,127 | -127,127 |
| 12 | 2570,333 | -95,3331 |
| 13 | 2522,066 | 30,93408 |
| 14 | 2254,422 | 353,5778 |
| 15 | 2401,845 | 174,1545 |
| 16 | 2454,802 | -164,802 |
| 17 | 2207,844 | 40,15589 |
| 18 | 2367,664 | -213,664 |
| 19 | 2205,343 | -127,343 |
| 20 | 2532,524 | 57,47573 |
| 21 | 2469,811 | 76,189 |
| 22 | 2056,129 | 52,87146 |
| 23 | 2302,117 | 95,8829 |
| 24 | 2136,814 | 105,186 |
| 25 | 2419,208 | -210,208 |
Предположим, что между результирующим и факторными признаками существует линейная связь, выраженная уравнением:
У = а0 + a1x1 +a2x2
Для расчета коэффициентов а0; a1; a2 применим метод наименьших квадратов.
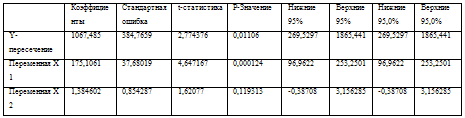
а0= 1067,5
а1= 175,1
а2= 1,38
Следовательно, модель имеет следующий вид:
У=1067,5+175,1Х1+1,38Х2
1 шаг. Проверка на мультиколлинеарность
Наиболее распространенным методом исследования модели на мультиколлинеарность является метод Феррара-Глобера.
Проводим стандартизацию факторов:
X1 |
X2 |
X |
X |
X |
X2- |
X1* |
X2* |
| 464,4 | 69 | 215667,4 | 4761 | 10,284 | 8,68 | 0,05 | 0,12 |
| 407,8 | 46 | 166300,8 | 2116 | -46,316 | -14,32 | -0,25 | -0,21 |
| 426,3 | 51 | 181731,7 | 2601 | -27,816 | -9,32 | -0,15 | -0,13 |
| 508,2 | 84 | 258267,2 | 7056 | 54,084 | 23,68 | 0,29 | 0,34 |
| 547,7 | 90 | 299975,3 | 8100 | 93,584 | 29,68 | 0,50 | 0,43 |
| 474,1 | 55 | 224770,8 | 3025 | 19,984 | -5,32 | 0,11 | -0,08 |
| 387,5 | 42 | 150156,3 | 1764 | -66,616 | -18,32 | -0,35 | -0,26 |
| 500,3 | 76 | 250300,1 | 5776 | 46,184 | 15,68 | 0,24 | 0,22 |
| 429,4 | 43 | 184384,4 | 1849 | -24,716 | -17,32 | -0,13 | -0,25 |
| 493,5 | 56 | 243542,3 | 3136 | 39,384 | -4,32 | 0,21 | -0,06 |
| 448 | 61 | 200704 | 3721 | -6,116 | 0,68 | -0,03 | 0,01 |
| 516,3 | 87 | 266565,7 | 7569 | 62,184 | 26,68 | 0,33 | 0,38 |
| 443,5 | 61 | 196692,3 | 3721 | -10,616 | 0,68 | -0,06 | 0,01 |
| 439,9 | 66 | 193512 | 4356 | -14,216 | 5,68 | -0,08 | 0,08 |
| 445,2 | 66 | 198203 | 4356 | -8,916 | 5,68 | -0,05 | 0,08 |
| 470,8 | 58 | 221652,6 | 3364 | 16,684 | -2,32 | 0,09 | -0,03 |
| 444,2 | 47 | 197313,6 | 2209 | -9,916 | -13,32 | -0,05 | -0,19 |
| 471,1 | 64 | 221935,2 | 4096 | 16,984 | 3,68 | 0,09 | 0,05 |
| 417,1 | 42 | 173972,4 | 1764 | -37,016 | -18,32 | -0,20 | -0,26 |
| 463,7 | 79 | 215017,7 | 6241 | 9,584 | 18,68 | 0,05 | 0,27 |
| 443,7 | 62 | 196869,7 | 3844 | -10,416 | 1,68 | -0,06 | 0,02 |
| 435,8 | 50 | 189921,6 | 2500 | -18,316 | -10,32 | -0,10 | -0,15 |
| 461,7 | 54 | 213166,9 | 2916 | 7,584 | -6,32 | 0,04 | -0,09 |
| 392,9 | 43 | 154370,4 | 1849 | -61,216 | -17,32 | -0,32 | -0,25 |
| 419,8 | 56 | 176232 | 3136 | -34,316 | -4,32 | -0,18 | -0,06 |
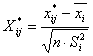 ,
, ![]()
Составляем матрицу В* = X*TX*.
![]() ;
;
Рассчитаем фактическое
значение ![]() для расчетной матрицы:
для расчетной матрицы:
![]()
Находим критическое значение
![]() :
:
![]() ,
, ![]() ,
, ![]() .
.
Сравнивая полученные
значения, ![]() приходим к выводу, что в массиве
факторных переменных мультиколлиниарность не существует.
приходим к выводу, что в массиве
факторных переменных мультиколлиниарность не существует.