Реферат: Основні властивості простору Соболєва

Реферат

Основні властивості простору Соболєва

Зміст

1. Простір Соболєва

1.1 Загальне визначення

1.2 Простір

1.3 Інше визначення узагальненої похідної

1.4 Найпростіша теорема вкладення

1.5 Простір Соболєва  й

2. Застосування просторів Соболєва в математичній фізиці

2.1 Доказ існування й одиничності узагальненого рішення рівняння Лапласа

Висновок

Список літератури

1. Простір Соболєва

1.1 Загальне визначення

Нехай у  задана замкнута обмежена область  Розглянемо лінійний простір речовинних функцій   раз безупинно диференцюємих на  Диференцюємость на замкнутій області  можна розуміти в різних змістах. Ми будемо припускати, що у  функції   раз безупинно диференцюємі, причому кожна частинна похідна функції  має межу при прагненні  до будь-якої граничної крапки області  так що в результаті її продовження на  вона стає безперервної в  Границя  області  передбачається досить гладкої. Крім того, звичайно ми будемо вважати область  одно зв'язковий і задовольняючому такому додатковому обмеженням, які можуть знадобитися в тих або інших міркуваннях.

Скористаємося для стислості наступними позначеннями. Набір індексів  називається мультиіндексом. Число  називається довжиною мультиіндекса. Для позначення часток похідних приймемо

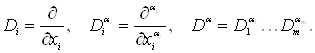
Уведемо в розглянутому вище лінійному просторі норму

(1.1)

Отриманий нормований простір позначається  Його поповнення в нормі (1.1) позначається  й називається простором Соболєва.

У прикладних задачах досить часто зустрічається випадок  Загальноприйнятий наступне позначення:  Простір Соболєва  є гильбертовим простором – поповненням простору  в нормі, породженої скалярним добутком

Нижче ми докладніше зупинимося на окремих випадках  і  тобто розглянемо простору Соболєва на речовинній осі й у тривимірному просторі.

1.2 Простір

Розглянемо на відрізку  простір  який складається із усіляких функцій  безупинно диференцюємих на  зі скалярним добутком

(1.2)

і відповідному цьому скалярному добутку нормою

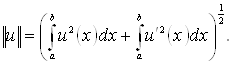(1.3)

 є поповненням  у цій нормі. Елементами  відповідно до теореми про поповнення, є класи, що складаються з послідовностей  фундаментальних в  у середньому, точніше, таких, що

 при

Дві такі послідовності  й  належать одному класу, якщо  є нескінченно малою по нормі  тобто, якщо

 при

З умови фундаментальності в середньому  в  треба, що окремо при

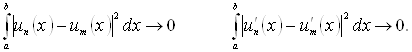
Аналогічно, з умови еквівалентності  й  по нормі  треба, що при

Відповідно до визначення простору  існують функції  й  такі, що при   а  в середньому.

Ми приходимо до наступного найважливішого визначення. Нехай  Тоді у  визначені елемент  із представником  і елемент  із представником   називається узагальненій похідній (у змісті Соболєва) від  При цьому пишуть:

З визначення узагальненій похідній  видно, що вона визначається не локально, в окремих крапках, а глобально – відразу на всім відрізку  Нехай  так що   Перейдемо до межі при  в рівностях

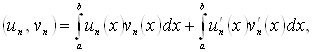(1.4)

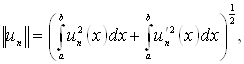(1.5)

і, відповідно до теореми про поповнення й визначення інтеграла Лебега, прийдемо до формул (1.2) і (1.3), де тепер похідні розуміються в узагальненому змісті, а інтеграл – у змісті Лебега. Для конкретних обчислень, зрозуміло, можна й потрібно користуватися формулами (1.4) і (1.5), взявши досить велике  тобто замість ідеальних елементів     скористатися їхніми гладкими наближеннями    

1.3 Інше визначення узагальненої похідної

Нехай  – множина всіх безупинно диференцюємих на відрізку  фінітних функцій  Якщо тепер  безупинно дференцюєма на відрізку  те для довільної функції  справедливо наступна інтегральна тотожність:

(1.6)

перевіряється інтегруванням вроздріб. Цією тотожністю  повністю визначається.

Допустимо, що, крім того, для будь-яких  і деякої безперервної на відрізку  функції

(1.7)

Віднімаючи ці тотожності, одержимо, що для будь-яких

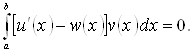
Звідси, внаслідок щільності  в   на відрізку  Виявляється, інтегральна тотожність (1.7) можна прийняти за визначення узагальненої похідної. Насамперед, справедлива наступна лема.

Лема 1. Якщо  то для будь-яких  справедливо тотожність (1.6).

Доказ. Нехай  тоді для всіх  маємо (1.6):

Внаслідок властивості безперервності скалярного добутку в останній рівності можна перейти до межі при  В результаті ми одержимо тотожність (1.6) для будь-якої функції  Лема доведена.

Лема 2. Нехай дані   такі, що для всіх  справедливо тотожність (1.7). Тоді  (узагальнена похідна).

Доказ. Нехай  а  Тоді

при

для будь-якого

Нехай  – клас, представником якого є

Тоді

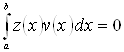
для будь-яких  Звідси  Лема доведена.

1.4 Найпростіша теорема вкладення

Теорема 1.  вкладено в

Доказ. Нехай  безупинно дференцюєма на відрізку  Відповідно до теореми про середній, внаслідок безперервності  найдеться крапка  така, що 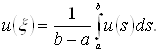 Тому на відрізку  справедливо наступна тотожність:

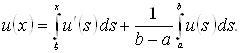
За допомогою нерівності Коші-Буняковського маємо

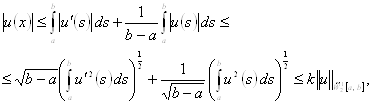
де

Отже, для будь-який безупинно дференцюємої на відрізку  функції  справедлива нерівність

(1.8)

Нехай тепер послідовність  – фундаментальна по нормі  Тоді

при  Отже,  фундаментальна в змісті рівномірної збіжності й, за критерієм Коші рівномірної збіжності, сходиться до  Тим більше  в середньому. Таким чином, у класі з  утримуючої  як представник, утримується безперервна функція  й, виходить, цей клас можна ототожнити з  Ототожнимо елементи  з безперервними функціями. Нехай  Переходячи в нерівності  до межі при  прийдемо до нерівності (1.8).

Отже, вкладення  в  доведено. Доказ теореми закінчений.

1.5 Простір Соболєва  й

Нехай  – однозв'язна область із досить гладкою границею  В замкнутій області  розглянемо лінійний простір усіляких безупинно диференцюємих функцій  зі скалярним добутком

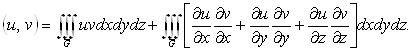
При цьому

(1.9)

Отриманий простір зі скалярним добутком позначається  а його поповнення – це, по визначенню, простір Соболєва

Нехай  – фундаментальна послідовність у  тобто  при  Звідси треба, що в  будуть фундаментальними послідовності

Внаслідок повноти  в  є елементи, які ми позначимо

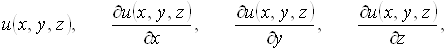
так що при  в середньому

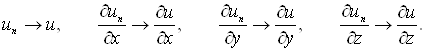
Елементи 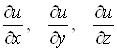 називаються узагальненими частками похідними елемента

Скалярний добуток і норма задаються в  тими ж формулами, що й в  у які тепер похідні узагальнені, а інтегрування розуміється в змісті Лебега. Уведемо в розгляд простір  Цей простір є поповненням у нормі

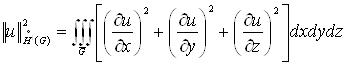(1.10)

лінійного простору функцій, безупинно диференцюємих на  й таких, що   є гильбертовим простором зі скалярним добутком

Лема 3. Якщо  а  те

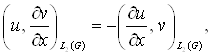
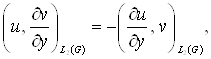
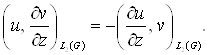
Доказ. Досить довести першу із цих формул. Вона справедлива, якщо  а  Нехай  – фундаментальна в  послідовність, межу якої – елемент  Переходячи в тотожності 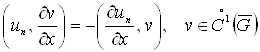 до межі при  одержимо для будь-який  Дійсно, зі збіжності в  треба, що

тобто безперервність скалярного добутку.

Нехай тепер  – фундаментальна послідовність у  Перейдемо до межі в тотожності

й одержимо вихідну тотожність.

Наслідок.  утримується строго усередині

Дійсно, функція  Але  інакше ми мали б

тобто

для кожної  Візьмемо  й одержимо протиріччя.

Теорема 2 (Фридрихс). Існує постійна  така, що для будь-яких

Доказ. По самому визначенню  всякий елемент із  належить  Нехай  і сходиться в  до

Побудуємо куб

утримуючу область Функції  визначимо нулем у  Частинна похідна  існує всюди в  за винятком, бути може, тих крапок, у яких пряма, паралельна осі абсцис, перетинає границю  області  Для будь-якої крапки  маємо

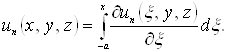
По нерівності Коші-Буняковського

Інтегруючи отриману нерівність по  знаходимо

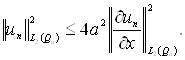
Тому що  поза  те

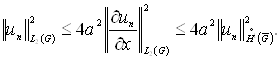
Переходячи до межі при  приходимо до доказуваної нерівності Фридрихса.

Наслідок 1. Простір  вкладений в

Це пропозиція безпосередньо випливає з визначення вкладення банахових просторів і нерівності Фридрихса.

Наслідок 2. У  норми (1.9) і (1.10) еквівалентні.

Дійсно, використовуючи нерівність Фридрихса, маємо

2. Застосування просторів Соболєва в математичній фізиці

2.1 Доказ існування й одиничності узагальненого рішення рівняння Лапласа

Теорема 3 (Рисс). Нехай  – гильбертовий простір. Для будь-якого лінійного обмеженого функціонала  заданого всюди на  існує єдиний елемент  такий, що для всіх  

При цьому

Доказ наведений в [1, стор. 171].

Теорема Рисса ефективно застосовується в теорії можливості розв'язання граничних задач для рівнянь із частками похідними. Будемо говорити, що гильбертовий простір  вкладений у гильбертовий простір  якщо із  треба, що  причому існує постійна  така, що для всіх

(2.1)

Має місце наступний наслідок з теореми Рисса.

Теорема 4. Якщо гильбертовий простір  вкладений у гильбертовий простір  то для кожного елемента  найдеться єдиний елемент  такий, що для всіх  має місце тотожність

Тотожність це визначає оператор  такий, що  при цьому

Доказ. При кожному фіксованому  вираження  при всіляких  визначає лінійний обмежений функціонал на  Лінійність функціонала очевидна. Його обмеженість випливає з оцінки

По теоремі Рисса існує єдиний елемент  такий, що  Тим самим усюди на  заданий лінійний оператор  Далі, з доведеного вище нерівності треба, що

Думаючи тут  одержимо  тобто  й, виходить,  обмежений. Теорема доведена.

Як додаток доведеної теореми й просторів Соболєва доведемо існування й одиничність узагальненого рішення задачі Дирихле для рівняння Пуассона. У замкнутої обмеженої однозв'язної області  з досить гладкою границею  розглянемо наступну граничну задачу:

(2.2)

(2.3)

Припустимо, що права частина  безперервна в  по сукупності змінних. Функція  називається класичним рішенням задачі (2.2) – (2.3), якщо  безперервно як функцію трьох змінних у  має в  безперервні похідні, що входять у ліву частину (2.2), задовольняє в  рівнянню (2.2) і дорівнює нулю на  тобто задовольняє граничній умові (2.3).

Нехай  – класичне рішення задачі (2.2) – (2.3), а  безперервна в  дорівнює нулю на  й безупинно дференцюєма в  тоді для будь-який такий  справедливо наступна інтегральна тотожність:

(2.4)

Для доказу цієї тотожності скористаємося формулою Гаусса-Остроградського:

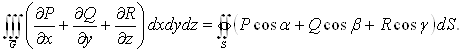
Приймемо

   й одержимо

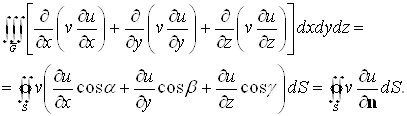
Оскільки

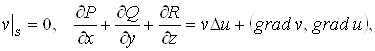
а  те одержуємо (2.4).

Нехай тепер   а інтеграли (2.4) розуміються в змісті Лебега. Функція  називається узагальненим рішенням крайової задачі (2.2) – (2.3), якщо для будь-якої функції  виконується інтегральна тотожність (2.4).

Доведемо, що для будь-якої правої частини  узагальнене рішення крайової задачі (2.2) – (2.3) існує і єдино.

Для цього помітимо, що гильбертовий простір  вкладений у гильбертовий простір  тому що, по визначенню  всяка функція  належить також і  й справедлива оцінка для кожної  (див. п. 1.5):

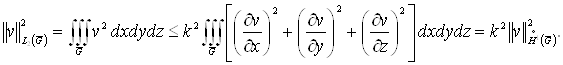
Отже, по теоремі 4 для всякої функції  існує єдина функція  така, що для всіх

а це і є інтегральну тотожність (2.4).

Висновок

Простір Соболєва  й тісно пов'язане з ним поняття узагальненої похідної в сенсі Соболєва були уведені в математичну практику академіком С.Л. Соболєвим і відіграють найважливішу роль у теоретичних і прикладних питаннях математичної фізики й функціонального аналізу. Поповнення простору гладких функцій  деякими ідеальними елементами, які можна з будь-яким ступенем точності обчислити за допомогою елементів із  приводить, з одного боку, внаслідок повноти  до точності й закінчення багатьох математичних тверджень, а з іншого боку, зберігає всі обчислювальні можливості.

Таким чином, ми розглянули простори Соболєва, їхні основні властивості й застосування в математичній фізиці.

Список літератури

1. Треногін В.О. Функціональний аналіз. – К., 2006

2. Соболєв С.Л. Деякі застосування функціонального аналізу в математичній фізиці. – К, 2004

3. Куланін Е.Д., Норін В.П. 3000 конкурсних задач по математиці. – К., 2000

4. Гусєв В.А., Мордкович А.Д. Довідкові матеріали по математиці. – К., 2003

5. Сканаві М.М. Збірник задач по математиці. – К., 2006