Контрольная работа: Вычисление случайных величин
Задача №1.
Двумерная случайная величина (X,Y) имеет равномерное распределение вероятностей в треугольной области ABC:
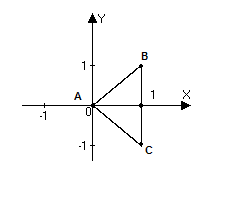
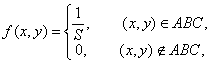
где S – площадь треугольника ABC.
Определить плотности
случайных величин X и Y, математические ожидания M(X) и M(Y), дисперсии D(X) и D(Y), а также коэффициент корреляции 
.
Являются ли случайные величины X и Y независимыми?
Решение.
Разделим область ABC на две равные части вдоль оси OX, тогда из условия
или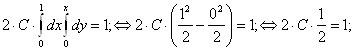 
следует, что 
Тогда плотность двумерной случайной величины (X,Y):
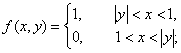
Вычислим плотность составляющей X:
при 
, 
откуда плотность составляющей X –
Вычислим плотность составляющей Y:
при 
, 
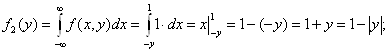
при 
, 
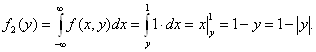
Поэтому плотность составляющей Y –
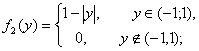
Найдем условную плотность составляющей X:
при 
, 
случайные величины X и Y зависимы.
Найдем математическое ожидание случайной величины X:
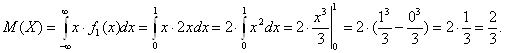
Найдем дисперсию случайной величины X:
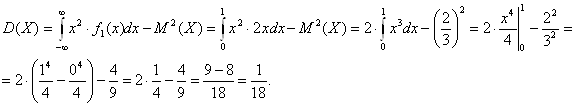
Найдем среднеквадратическое отклонение случайной величины X:
Найдем математическое ожидание случайной величины Y:
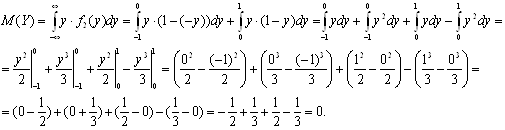
Найдем дисперсию случайной величины Y:
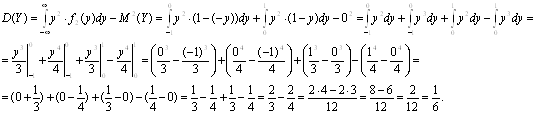
Найдем среднеквадратическое отклонение случайной величины Y:
Найдем математическое ожидание двумерной случайной величины (X,Y):
Тогда ковариация: 
,
а значит и коэффициент
корреляции 
Следовательно, случайные величины X и Y - зависимые, но некоррелированные.
Задача №2
Двумерная случайная величина (X,Y) имеет следующее распределение вероятностей:
| Y | X | |||
| 3 | 6 | 8 | 9 | |
| -0,2 | 0,035 | 0,029 | 0,048 | 0,049 |
| 0,1 | 0,083 | 0,107 | 0,093 | 0,106 |
| 0,3 | 0,095 | 0,118 | 0,129 | 0,108 |
Найти коэффициент корреляции между составляющими X и Y.
Решение.
Таблица распределения вероятностей одномерной случайной величины X:
| X | 3 | 6 | 8 | 9 |
|
|
0,213 | 0,254 | 0,270 | 0,263 |
Проверка: 
+ 
+ 
+ 
= 0,213 + 0,254 + 0,270 + 0,263
= 1.
Таблица распределения вероятностей одномерной случайной величины Y:
| Y | -0,2 | 0,1 | 0,3 |
|
|
0,161 | 0,389 | 0,450 |
Проверка: 
+ 
+ 
= 0,161 + 0,389 + 0,450 = 1.
Вычислим числовые характеристики случайных величин X и Y.
1. Математическое ожидание случайной величины X:
2.
Математическое ожидание случайной величины Y:
3. Дисперсия случайной величины X:
4. Дисперсия случайной величины Y:
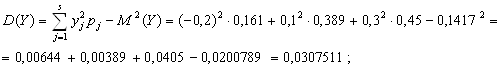
5. Среднеквадратическое отклонение случайной величины X:
6. Среднеквадратическое отклонение случайной величины Y:
Таблица распределения вероятностей случайной величины X-M(X):
| X-M(X) | 3-M(X) | 6-M(X) | 8-M(X) | 9-M(X) |
|
|
0,213 | 0,254 | 0,270 | 0,263 |
Таблица распределения вероятностей случайной величины Y-M(Y):
| Y-M(Y) | -0,2-M(Y) | 0,1-M(Y) | 0,3-M(Y) |
|
|
0,161 | 0,389 | 0,450 |
Таблица распределения вероятностей случайной величины [X-M(X)][Y-M(Y)]:
| [X-M(X)][Y-M(Y)] | 1,260873 | 0,153873 |
| P | 0,035 | 0,083 |
| -0,584127 | 0,235773 | 0,028773 | -0,109227 | -0,447627 |
| 0,095 | 0,029 | 0,107 | 0,118 | 0,048 |
| -0,054627 | 0,207373 | -0,789327 | -0,096327 | 0,365673 |
| 0,093 | 0,129 | 0,049 | 0,106 | 0,108 |
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Найдем ковариацию:
Найдем коэффициент корреляции:
Ответ: -0,028.
Задача №3
|
Рост, см (X) |
Вес, кг (Y) | |||||
| 22,5-25,5 | 25,5-28,5 | 28,5-31,5 | 31,5-34,5 | 34,5-37,5 | ||
| 117,5-122,5 | 1 | 3 | - | - | - | |
| 122,5-127,5 | - | 2 | 6 | 1 | - | |
| 127,5-132,5 | - | 1 | 5 | 5 | - | |
| 132,5-137,5 | - | 1 | 6 | 7 | 2 | |
| 137,5-142,5 | - | - | 1 | 4 | 2 | |
| 142,5-147,5 | - | - | - | 1 | 1 | |
| 147,5-152,5 | - | - | - | - | 1 | |
Результаты обследования 50 учеников:
По данным таблицы требуется:
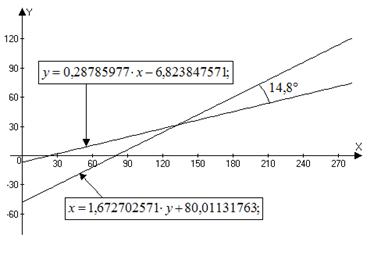
- написать выборочные уравнения прямых регрессии Y на X и X на Y;
- вычертить их графики и определить угол между ними;
- по величине угла между прямыми регрессии сделать заключение о величине связи между X и Y.
Решение.
Принимая рост всех учеников, попавших в данный интервал, равным середине этого интервала, а вес – равным середине соответствующего интервала, получим так называемую корреляционную таблицу:
Для роста X получим:
1. Выборочная средняя –
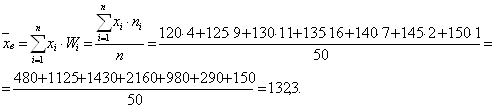
2. Дисперсия выборочная исправленная –
Для веса Y получим:
1. Выборочная средняя -
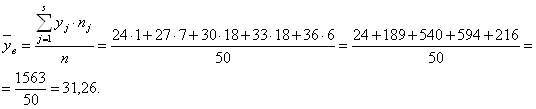
2. Дисперсия выборочная исправленная –
Найдем выборочный коэффициент корреляции:
Найдем значения коэффициентов регрессии:
Уравнение прямой регрессии Y на X имеет вид:
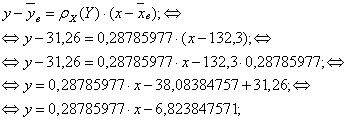
Уравнение прямой регрессии X на Y имеет вид:
- угол между прямыми регрессии.
Следовательно, связь между X и Y не тесная.
| Технология и автоматизация производства РЭА | |
|
2КОМИТЕТ РФ ПО ВЫСШЕМУ ОБРАЗОВАНИЮ 2МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ 2(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ) конспект лекций ... тематическое ожидание E(t 4i 0)=M[x(t 4i 0)] (71), где x(t 4i 0)- случайная вели- M(X) - математическое ожидание величины Х; d 5* 0 - выборочная дисперсия |
Раздел: Рефераты по радиоэлектронике Тип: реферат |
| Основные понятия статистики | |
|
ТЕМА 1.4. Законы распределения случайных величин, наиболее часто используемые в экономических приложениях, и их числовые характеристики 1. Основные ... Условным математическим ожиданием дискретной случайной величины Y при X = x (х - определенное возможное значение Х) называется произведение всех возможных значений Y на их условные ... Условное математическое ожидание M(Y/x)=f(x) является функцией от х и называется функцией регрессии Х на Y. |
Раздел: Рефераты по экономике Тип: учебное пособие |
| О теории вероятностей | |
|
1. Предмет и основные понятия ТВ ТВ - математическая наука изучающая закономерность в массовых однородных случаях, явлениях и процессах. Элементарные ... Пусть имеется непрерывная случайная величина X с функцией плотности вероятности f(x). Другая случайная величина Y связана со случайной величиной X функциональной зависимостью: Математическое ожидание и дисперсию СВ Y - функции случайной величины X(Y=ѭ(x)), имеющей дифференциальную функцию f(x), можно определить по формулам: |
Раздел: Рефераты по математике Тип: шпаргалка |
| Психологический словарь | |
|
Борис Гурьевич Мещеряков, Владимир Петрович Зинченко Большой психологический словарь Оглавление Предисловие Персоналии Список авторов Список ... Пусть m - число возможных альтернатив стимула (и ответов), P - наблюдавшаяся частота правильных ответов, тогда p, т. е. скорректированная частота правильных ответов, вычисляется по ... В записях A = B и B = A или y = kx и x = y/k правая и левая части имеют разный внешний вид, хотя сами записи содержат один и тот же набор символов. |
Раздел: Рефераты по психологии Тип: книга |
| Статистические наблюдения | |
|
ТЕМА 1. ПРЕДМЕТ, МЕТОД И ЗАДАЧИ СТАТИСТИКИ Gegenstand, Methoden und Aufgaben der Statistik Subject matter, methods and tasks of statistics 1.1 ... И среднее квадратическое отклонение, и дисперсия - показатели, широко применяемые в статистике, математической статистике и теории вероятностей. В последнем для расчета ѭ2 берут выровненные (т.е. рассчитанные по уравнению регрессии) значения результативного признака y. Теоретическое корреляционное отношение еще называют ... |
Раздел: Рефераты по экономике Тип: учебное пособие |