Реферат: Линейные метрические, нормированные и унитарные пространства

Линейные метрические, нормированные и унитарные пространства

Введение

При решении многих технических и прикладных задач радиотехники возникают вопросы: как объективно сравнить какой сигнал больше другого или как оценить "близость" двух сигналов.

Оказывается, что методы функционального анализа, создав стройную теорию сигналов, в основе которой лежит концепция сигнала как элемента специально сконструированного пространства, позволяют ответить на эти вопросы.

Введем обозначения. Если R – некоторое множество элементов, то f Î R означает, что f является элементом R;  или f Ï R означает, что f не принадлежит R.

Множество элементов х Î R, обладающих свойством А обозначается символом  например  - множество точек, принадлежащих полукругу х² + y² £ 1, x ³ 0.

Если M и N – два множества, то прямое произведение M х N этих множеств определяется следующим образом

то есть представляет собой множество всех упорядоченных пар (x, y), где x Î M, a y Î N.

1. Линейные метрические пространства

Множество R называется линейным пространством, если

1) в R определена операция "сложения", которая подчиняется всем правилам сложения: если f Î R, g Î R, то f + g Î R; в R имеется нулевой элемент 0 такой, что 0 +f = f для всех f Î R;

2) в R определена операция умножения элемента f Î R на числа a из множества К (a Î К, f Î R Þ a f Î R). Чаще всего К – множество всех действительных или комплексных чисел.

В дальнейшем будем рассматривать только линейные пространства.

Рассмотрим отображение Т, которое каждому элементу f Î R однозначно ставит в соответствие элемент h Î R*, где R* является также линейным пространством. Если R* = R, то Т отображает R в самого себя. Отображение Т называется оператором и отображение R в R* записывается в виде уравнения

T f = h (f Î R, h Î R*).

В частном случае, когда R* - пространство комплексных чисел, Т носит название функционала.

Пусть уравнение

T f = h

имеет единственное решение и каждому элементу h Î R* можно поставить в соответствие единственный элемент f Î R. Оператор, осуществляющий это соответствие, называется обратным по отношению к Т и обозначается Т^-1. Таким образом можно записать

f = T^-1 h.

Пример. Пусть имеется система линейных уравнений

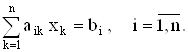
Представим эту систему в матричном виде

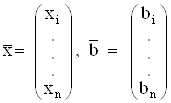
Если ввести пространство матриц – столбцов R, то  где

и  Здесь оператор А – матрица размера n x n

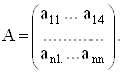
Если матрица А невырождена, то обратная матрица и является обратным оператором:

Определение. Линейное пространство R называется метрическим, если каждой паре элементов х, y Î R ставится в соответствие вещественное число r (x, y) – расстояние между x и y – удовлетворяющее условиям:

1.  r (x, y) ³ 0, если r (x, y) = 0, то x = y;

2.  r (x, y) = r (y, x);

3.  r (x, y) £ r (x, z) + r (z, y) (неравенство треугольника).

Если введением расстояния пространство R превращено в метрическое пространство, то говорят, что в пространстве R введена метрика.

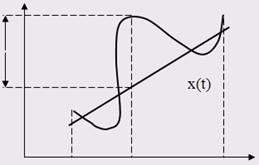
В радиотехнике элементами пространства являются сигналы (токи или напряжения), математическими моделями которых являются функции времени x(t), y(t), ... . Рассмотрим следующее пространство сигналов.

1. С_{[a, b]} - пространство непрерывных на промежутке [a, b] функций с метрикой:

 y(t)

r(x,y)

2. L²_{(a, b)} - пространство интегрируемых в квадрате функций (x(t) Î L²_{(a, b)}, если  с метрикой

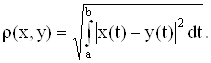
Определение. Элементы линейного пространства R называются линейно независимыми, если из условия

следует, что

a₁ = a₂ = . . . = a_n = 0.

В противном случае элементы f₁, f₂, . . . , f_n считаются линейно зависимыми.

Максимальное число линейно независимых элементов определяет размерность dim R пространства R и образуют базис этого пространства. Если m = dim R, то пространство обозначается R_m.

2.  Линейные нормированные пространства

Определение. Линейное пространство R называется нормированным, если каждому элементу х Î R ставится в соответствие вещественное число  ("длина" элемента х), называемое нормой х, которое удовлетворяет условиям:

1.  , тогда х = 0;

2.   (однородность нормы);

3.   (неравенство треугольника).

Положив для

превращаем нормированное пространство R в метрическое.

Можно и метрическое пространство R превратить в нормированное, если метрика удовлетворяет условиям:

 положив

Рассмотренные ранее пространства сигналов С_[a,b] и L²_(a,b) становятся соответственно нормированными, если

и  

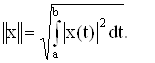
Если положить а = ¥, b = ¥, то квадрат этой нормы в теории сигналов носит название энергии сигнала.

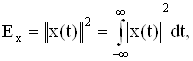
так как такая энергия выделяется на резисторе с сопротивлением в 1 Ом при напряжении x(t) на его зажимах.

Пример. Имеется треугольный импульс длительности t:

Вычислить энергию и норму сигнала.

Решение.

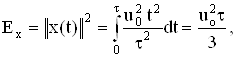
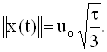
3.  Линейное унитарное пространство

Определение. Линейное нормированное пространство R называется унитарным, если в нем введено скалярное произведение, которое каждой паре элементов x, y Î R ставит в соответствие действительное или комплексное число (x, y), удовлетворяющее условиям

1. (x, y) = (y, x)* ( _* - знак комплексного сопряжения);

2. (a₁ х₁ + a₂ х₂, y) = a₁(x₁, y) + a₂(x₂, y) (a₁, a₂ Î K);

3. (x, x) ³ 0, если (х, х) = 0, то х = 0.

В унитарном пространстве норма вводится следующим образом

Теорема 1. Для " х, y унитарного пространства R справедливо неравенство Шварца

Равенство имеет место лишь для линейно зависимых элементов.

Теорема 2. Для " х, y унитарного пространства R имеет место неравенство

Равенство имеет место, если один из элементов х или y равен нулю или, когда х = l y (l > 0).

Теорема 3. Для " х, y унитарного пространства R выполняется равенство параллелограмма

Равенство имеет место, если один из элементов х или y равен нулю или, когда х = l y (l > 0).

Определение. Два элемента х, y Î R (x ¹ 0, y ¹ 0) называются ортогональными, если (х, y) = 0.

Система элементов e₁, e₂, . . . , e_n, . . . унитарного пространства R называется ортонормированной, если

Пусть система элементов х₁, х₂, . . . , х_n, . . . ортогональна ((x_i, x_j)=0, i ¹ j), тогда ее можно нормировать, положив

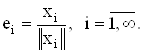
Из ортонормированности системы следует ее линейная независимость. Обратно – любую линейно независимую систему можно ортонормировать. Процесс ортонормированности следующий. Если система элементов y₁, y₂, . . . , y_n, . . . –линейно независимая, то система e₁, e₂, . . . , e_n, . . ., где

становится ортонормированной.

Пусть теперь f – любой элемент унитарного пространства R, a e₁, e₂, ..., e_n,... – ортонормированная система этого пространства. Величина

носит название коэффициента Фурье, а ряд

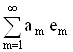
носит название ряда Фурье. Ряд Фурье наилучшим образом аппроксимирует f (приближается к f). Это значит, если рассматривать норму разности элемента f и ряда Фурье

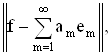
то наименьшее значение норма примет при

Можно показать, что выполняется неравенство

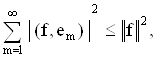
которое называется неравенством Бесселя.

Примеры ортонормированных систем:

1.  Система гармонических функций, записанных в комплексном виде

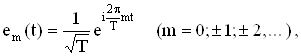
образуют ортонормированную систему в

2.  Функции

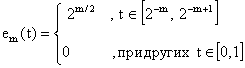
образуют для m = 1, 2, 3, ...ортонормированную систему, состоящую из неотрицательных функций на отрезке [0,1].

3. Ортонормированная система функций Уолша wal(m, x)  заданная на интервале 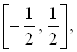 широко используется при дискретной обработке сигналов. Аналитическое описание функций Уолша довольно сложно. Легко понять принцип построения этих функций из графиков

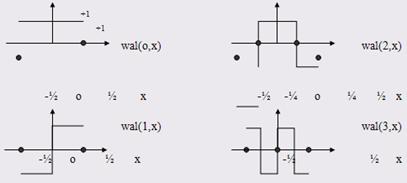
4. Важный класс ортонормированных систем можно получить при помощи ортогонализации функций 1, t, t², ..., tⁿ, ... в унитарном пространстве  со скалярным произведением

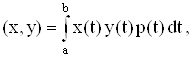
где р(t) – некоторая положительная, непрерывная на интервале [a, b] функция. Для отрезка [-1, 1] и p(t) = 1 получаем полиномы Лежандра; для отрезка [-1, 1] и - полиномы Чебышева первого рода; для полупрямой [0, ¥] и p(t) = е^-t – полином Лягерра; для всей оси (-¥, ¥) и p(t) = е^-t – полином Эрмита и т.д.

Определение. Линейное метрическое пространство R называется полным, если оно содержит все предельные точки. Это значит, если r(х_m+p, x_n) ® 0 при m ® ¥ (x_m Î R), " p = , то $ х_о Î R такое, что lim r(x_m, x_o) = 0.

m ®¥

Определение. Полное метрическое пространство называется пространством Банаха.

Полное унитарное пространство носит название пространства Гильберта.

Примеры.

1. Пространство L_{(a, b)} – абсолютно интегрируемых на интервале (а, b) функций (x(t) Î L_{(a, b)}, если 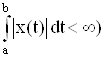 с метрикой

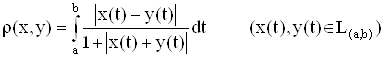
является пространством Банаха.

3.  Пространство L² _{(a, b)}, со скалярным произведением

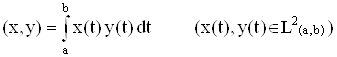
является пространством Гильберта.