Курсовая работа: Исследование электрических цепей при переходных процессах первого и второго рода

Курсовая работа по теме:

"Исследование электрических цепей при переходных процессах первого и второго рода"

Задача 1

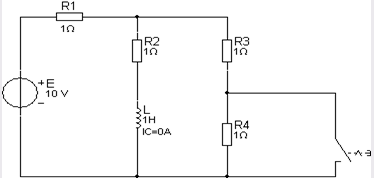
Решение

1) До коммутации:

Найдем :

По закону Ома:

Определим  в момент времени до коммутации:

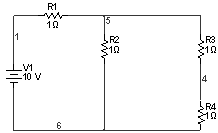
2) Установившийся

По закону Ома:

для этой схемы имеет вид:

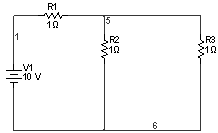
3) Переходный

 -

ур-е переходного процесса в общем виде

Первый закон коммутации:

Составляем характеристическое уравнение и определяем его корни через вычисление постоянной времени T:

Найдем постоянную интегрирование А:

Подставим значение характеристического уравнения  в общее уравнение в момент времени t=0:

Записываем уравнения:

Графики этих функций выглядит:

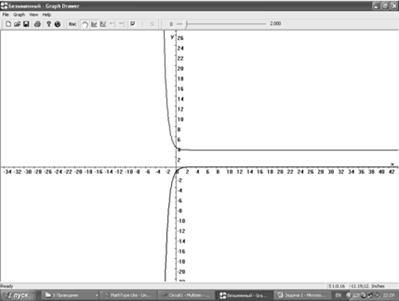
Для проверки результатов соберем в Multisim 10.0 указанную схему:

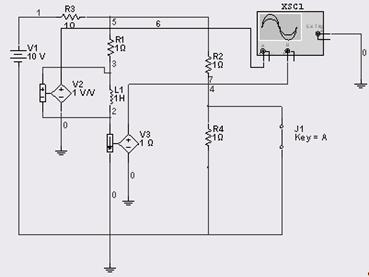
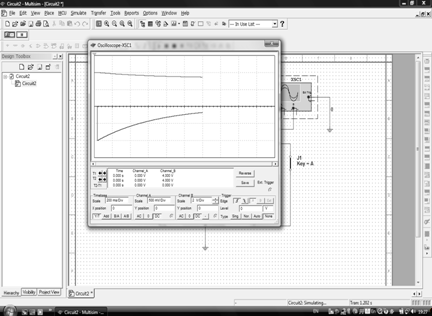
Задача 2

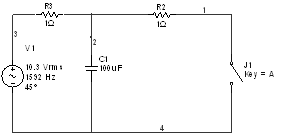
Решение

1) До коммутации:

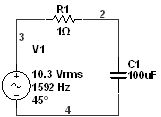
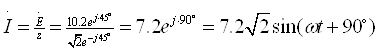
2) Установившийся

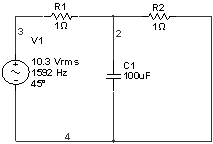
По закону Ома:

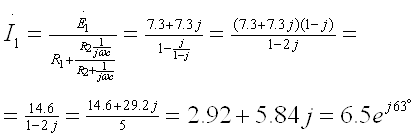
Делитель тока:

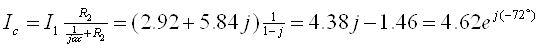
Напряжение на конденсаторе:

Уравнение ПП в общем виде:

Составляем характеристическое уравнение и определяем его корни через вычисление постоянной времени Т:

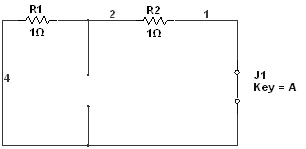
Второй закон коммутации:

Найдем постоянную интегрирования:

10,18=8,19+А

А=2

Записываем уравнения:

График:

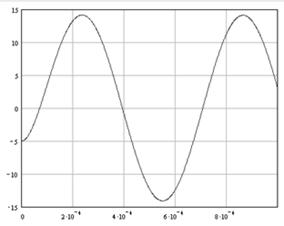
Мультисим:

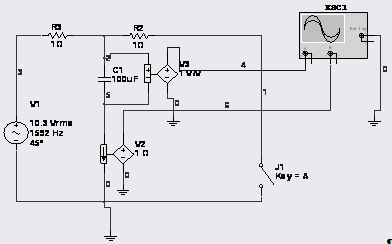
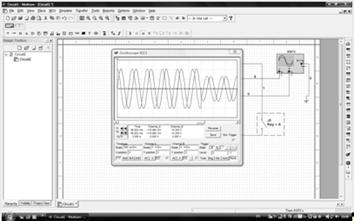
Задача 3

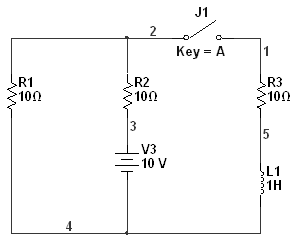
Решение

1) До коммутации:

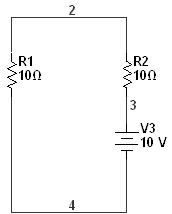
Определим в момент времени до коммутации:

Общее сопротивление этой цепи:

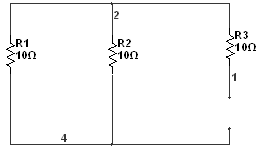
2) Установившийся

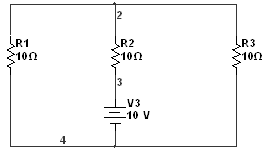
По закону Ома:

3) Переходной процесс

Уравнение ПП в общем виде:

Определяем корни характеристического уравнения через T:

Подставим значение р в общее уравнение в момент времени t=0

Записываем уравнения:

Графики:

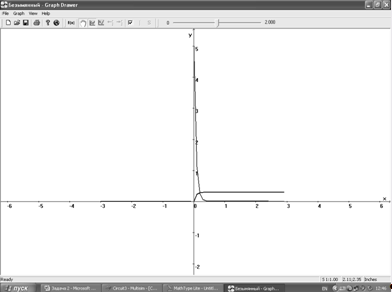
Мультисим:

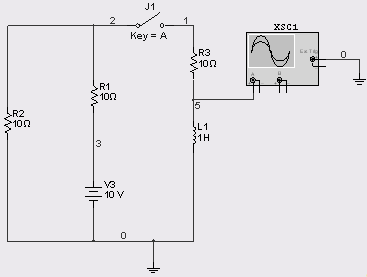
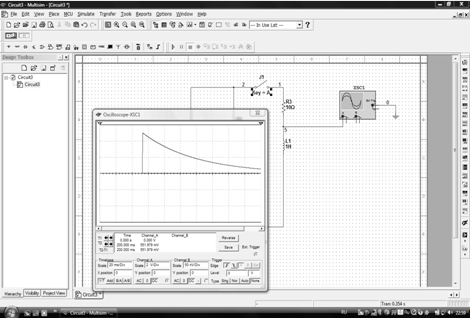
Задача 4

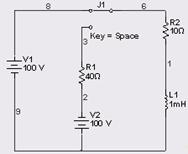
Решение

1) До коммутации:

По закону Ома:

2) Установившийся

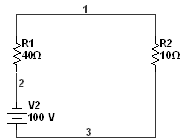
По закону Ома:

3) Переходный процесс

Записываем общее решение уравнения, в виде суммы установившейся и свободной составляющей:

Найдем постоянную интегрирования:

Записываем уравнения:

Графики:

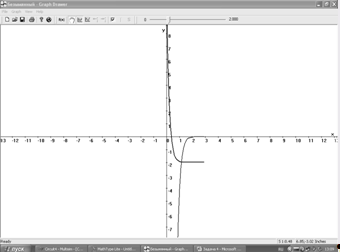
Мультисим:

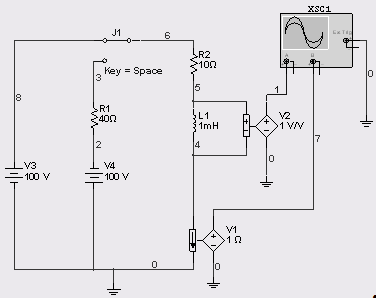
Задача 5

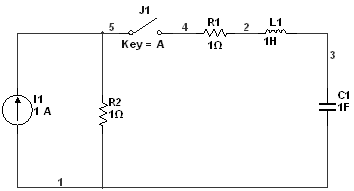
Решение (Классический метод)

1) До коммутации

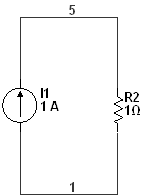
Закон коммутации:

Ключ разомкнут, ток через катушку и конденсатор не течет

2) Установившийся режим

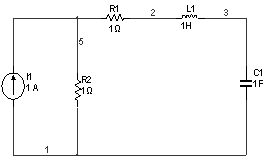
Преобразуем в схему с источником напряжения:

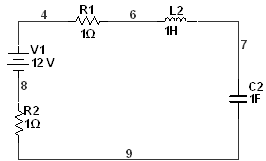
Входное сопротивление относительно ключа:

Составим операторную схему замещения:

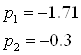
Корни разные, действительные, поэтому ищем свободную составляющую следующим образом:

Составим интегрально-дифференциальное уравнение по второму закону Кирхгофа:

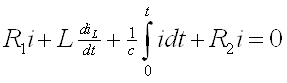
Продифференцировав его, получим диф. уравнение второго порядка:

Решение уравнения:

Аналогично для напряжения:

Находим  и :

0=1+ 

Получим систему уравнений:

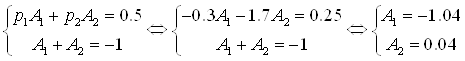
Уравнение ПП в общем виде:

Записываем уравнение:

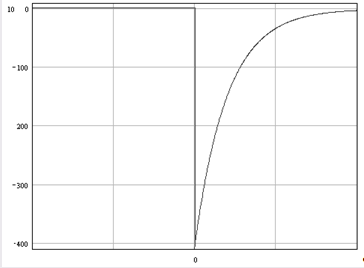
График:

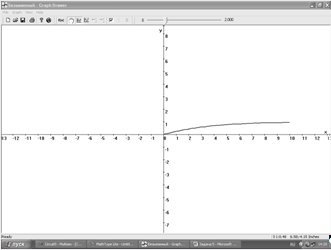
Операторный метод

1) До коммутации

2) После коммутации

Операторная схема замещения:

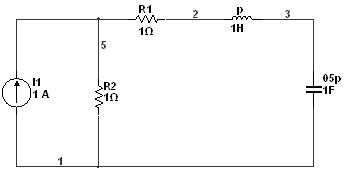
Операторное сопротивление цепи:

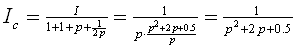
Найдем нули этой функции:

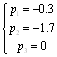
Запишем уравнение:

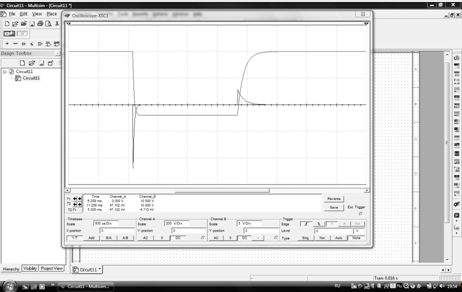
Мультисим:

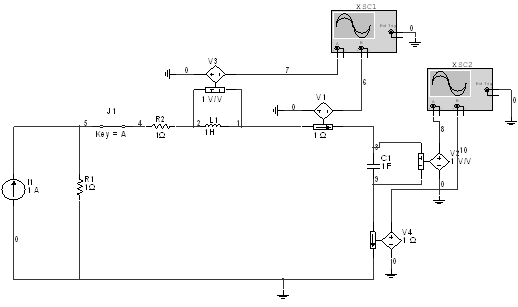
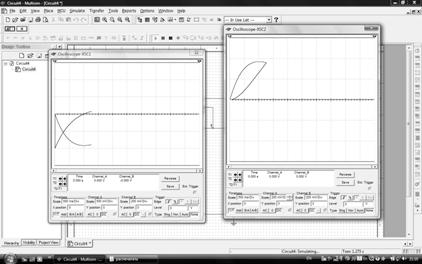
Задача 6

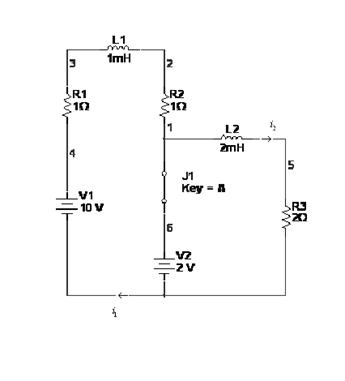
Решение (Классический метод)

1) До коммутации:

МКТ:

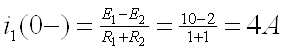
Найдем  в момент времени до коммутации

2) Установившийся

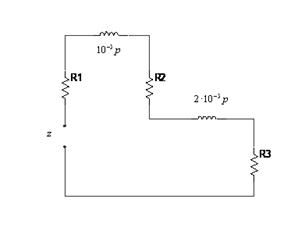
Входное сопротивление:

Найдем р

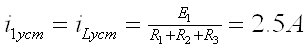
Собственный магнитный поток:

Закон сохранения магнитного потока

Составим систему уравнений, из которых найдем :

Найдем постоянную интегрирования А:

А=-0,5

Напряжение через индуктивность

Запишем уравнение:

Графики:

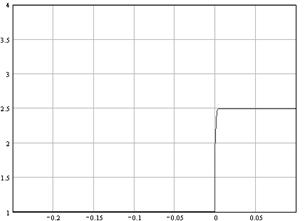
Для тока i₂

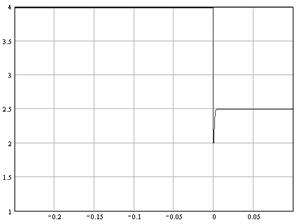
Для тока i₁

Операторный метод

1) До коммутации

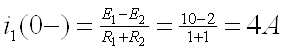
2) После коммутации

Общее напряжение в цепи:

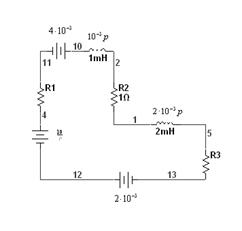
Заменим элементы цепи на их изображения

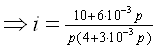
Найдем нули этой функции:

Запишем уравнения:

Мультисим: