Курсовая работа: Программа вычисления минимума заданной функции

Вычислить минимум функции F(x)=L(x1)x2-2.5L(x2)x-3 на отрезке [a;b] с точностью ε.

L(x1), L(x2) значения интерполяционного многочлена, построенного для таблично заданной функции f(x) в точках x1, x2.

Исходные данные:

a=0; b=2;

x1=0.041770;

x2=0.587282;

ε=10-4;

x 0 0.1 0.2 0.3 0.4 0.5 0.6
f(x) 1.858652 1.851659 1.851401 1.848081 1.841914 1.833125 1.821948

 

2. Постановка задачи и формализация

 

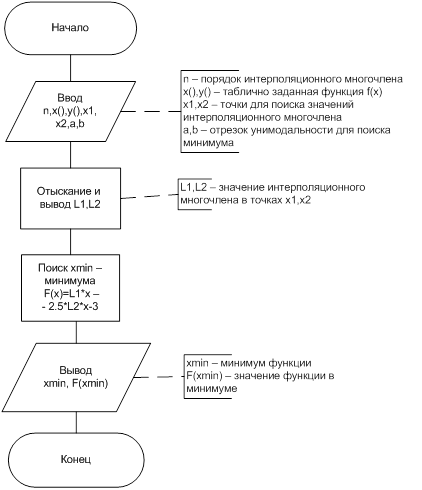
Для решения поставленной задачи необходимо разработать программные модули, выполняющие следующие действия:

- главный модуль, получающий исходные данные (таблично заданную f(x), a, b, x1, x2, ε), передающий их на обработку и выводящий промежуточные и конечные результаты (L(x1), L(x2), найденный минимум функции)

- модуль поиска значения интерполяционного многочлена L(x1), L(x2)

- модуль поиска минимума функции F(x) численным методом, использующий L(x1), L(x2) как коэффициенты при x2 и x

3. Выбор, обоснование, краткое описание методов

3.1 Поиск значений интерполяционного многочлена в точках x1 и x2

 

3.1.1 Постановка задачи

Требуется найти L(x1), L(x2) - значения интерполяционного многочлена, построенного для таблично заданной функции f(x) в точках x1,x2 Здесь решается задача аппроксимации, которая состоит в замене некоторой функции

у = f(х) другой функцией g(х,а0,а1,...,an) таким образом, чтобы отклонение g(х,а0,а1,...,an) от f(x) удовлетворяло в некоторой области (на множестве X) определенному условию. Этим условием является g(xi,a0,a1,…an)=f(xi) при i=0,n, которое означает, что аппроксимируемая функция f(x) совпадает с g(xi,a0,a1,…an) в т.н. узлах интерполяции x0,x1,…,xn. Это частный случай аппроксимации, называемый интерполяцией.

 

3.1.2 Выбор и описание метода

Задача интерполяции может быть решена множеством методов, среди которых:

1)  интерполяционный многочлен Лагранжа

интерполяционные формулы Ньютона Выберем для решения задачи интерполяции интерполяционный многочлен Лагранжа, так как его построение просто в алгоритмизации, не требует вычисления конечных разностей функции, , может быть умещено в одну небольшую процедуру – функцию.

Кроме того, метод Лагранжа работает и для неравноотстоящих интерполяционных узлов, к тому же не имеет различий, если точки x1 и x2 для поиска значений L(x1), L(x2) лежат в начале или в конце отрезка, где таблично задана функция.

Описание метода:

Задача интерполяции будем решать построением многочлена Лагранжа, который имеет вид:

 

Степень многочлена n обеспечивается n+1 интерполяционным узлом. Для задания таблицы значений функции будем использовать два массива x() и y(). Полином должен удовлетворять условию Ln(xi)=y(i)

3.2 Поиск минимума функции F(x) на отрезке [a;b]

 

3.2.1 Постановка задачи

Необходимо численным методом найти минимум функции F(x)=L(x1)x2-2.5L(x2)x-3

на отрезке [a;b] с точностью ε, при том, что L(x1) и L(x2) – коэффициенты, полученные вычислением полинома Лагранжа в т очках x1, x2. Это задача одномерной оптимизации.

Выбор метода: Для решения задачи одномерной оптимизации существует множество методов, среди которых:

1)  метод прямого перебора

2)  метод дихотомии

3)  метод золотого сечения

4)  метод Фибоначчи

5)  метод касательных

6)  метод Ньютона

оптимизация методом квадратичной интерполяции Выберем метод дихотомии, т.к. он прост в алгоритмизации, обеспечивает быструю сходимость (на каждой итерации отрезок неопределённости сужается почти вдвое). Его недостаток в виде необходимости многократного вычисления F(x) не играет особой роли, т.к. F(x) – обыкновенный полином и расчёт его значений не затратит много ресурсов ПК.

Описание метода:

Пусть f(x)- унимодальная на [a;b] и требуется найти минимум f(x) с абсолютной погрешностью Е. Идея метода дихотомии состоит в проведении на каждой итерации двух отсчётов (вычислений значений функции), отстоящих от середины отрезке неопределённости [а;b] на величину de[0;2E] и сравнения значения исследуемой функции в двух точках х(n-1) и

x(n-1). определяемых рекуррентными формулами:

Если

, то  

Иначе

 

N = 1,2,...- номер итерации, а0=а , b0 = b .

Вычисления проводятся до тех пор, пока b-а >Е.

Тогда с абсолютной погрешностью, не превосходящей Е, полагают

x*=(aN+bN)/2


Длина конечного отрезка неопределённости:

L0=b-a – длина начального отрезка

На каждой итерации отрезок неопределённости [aN;bN] уменьшается примерно вдвое. Число отсчётов функции n и число итераций N связаны соотношением N=n/2

Практически величина d выбирается из условий различимости двух отсчётов функции

Процедура поиска минимума методом дихотомии использует большее количество отсчётов функции для локализации точки минимума на отрезке заданной длины.

 

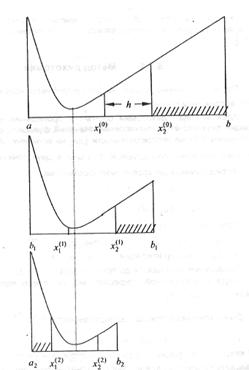
Геометрическая иллюстрация метода дихотомии


4. Проверка условий сходимости методов. Поиск значений интерполяционного многочлена в точках x1 и x2

Для правильной работы этого метода необходимо, чтобы функция была ограничена на отрезке интерполирования. Выполнение этого условия очевидно по заданию.

Условия унимодальности на отрезке [a;b] (первая производная возрастает, вторая больше нуля) выполняются, следовательно, отрезок [a;b] остаётся таким же как по заданию [0;2]


5. Тестирование программных модулей

 

5.1 Тестирование модуля поиска значений интерполяционного многочлена в точках x1 и x2

Рассчитаем значения функции f(x)=x2, заданной в виде таблицы

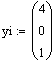
в точках x1=-1, x2=0.5. Т.к. исходная функция – полином, то интерполирующая будет ей в точности соответствовать и f(x.1)=L(x1)=1, f(x2)=L(x2)=0.25

 

Схема алгоритма управляющей программы

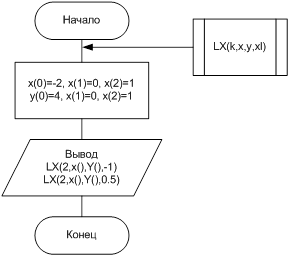
Схема алгоритма модуля поиска значений интерполяционного многочлена в точкe xl


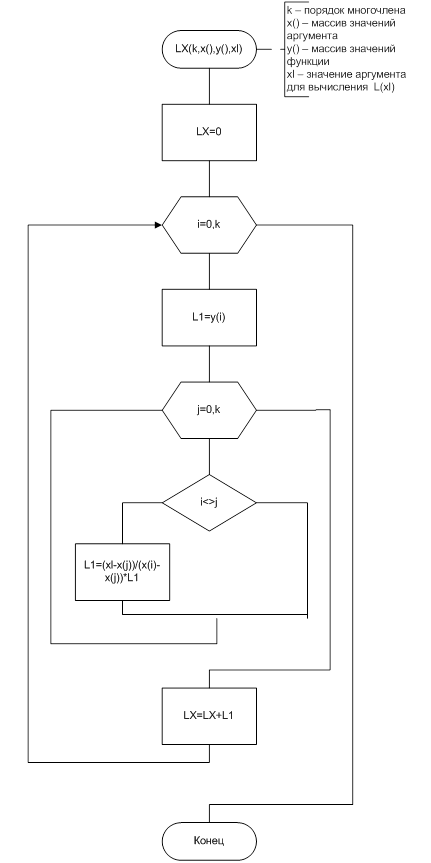
5.1.1 Код тестирующей программы

DECLARE FUNCTION LX (k, x(), y(), xl)

CLS

LOCATE 1, 15

PRINT "Kursovaya rabota po informatike OTLADKA"

LOCATE 2, 18

PRINT "Gruppa PS0601, Adamskiy Alexey"

DIM x(0 TO 2) AS SINGLE

DIM y(0 TO 2) AS SINGLE

x(0) = -2: x(1) = 0: x(2) = 1

y(0) = 4: y(1) = 0: y(2) = 1

PRINT

PRINT TAB(20); "L(x1)=f(x1)="; LX(2, x(), y(), -1)

PRINT TAB(20); "L(x2)=f(x2)="; LX(2, x(), y(), .5)

END

FUNCTION LX (k, x(), y(), xl)

l = 0 FOR i = 0 TO k L1 = y(i) FOR j = 0 TO k IF i <> j THEN L1 = L1 * (xl - x(j)) / (x(i) - x(j)) NEXT j l = l + L1 NEXT i

LX = l

END FUNCTION

 

Результат тестирования

Модуль отработал верно.

5.2 Тестирование модуля поиска минимума функции F(x) на отрезке [a;b]

программный модуль минимум функция

Проверим работоспособность модуля, найдя с его помощью минимум функции F(x)=x2 на отрезке [a;b]. Очевидно, что xmin=0, F(xmin)=0.

 

5.2.1 Схема алгоритма тестирующей программы:

 

Схема алгоритма управляющей программы

 

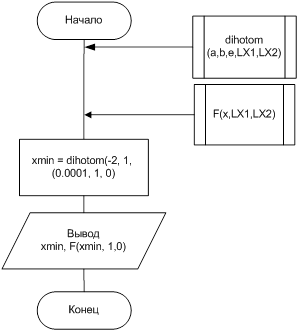
Схема алгоритма модуля f(x,LX1,LX2)

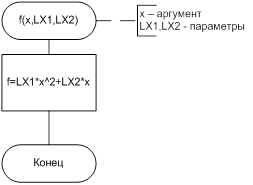
5.2.2 Код тестирующей программы

DECLARE FUNCTION dihotom (a, b, e, LX1, LX2)

DECLARE FUNCTION F (xmin, LX1, LX2)

CLS

LOCATE 1, 15

PRINT "Kursovaya rabota po informatike OTLADKA"

LOCATE 2, 18

PRINT "Gruppa PS0601, Adamskiy Alexey"

PRINT

xmin = dihotom(-2, 1, .0001, 1, 0)

PRINT TAB(10); "Minimum F(x): xmin="; xmin; "F(xmin)="; F(xmin, 1, 0)

END

FUNCTION dihotom (a, b, e, LX1, LX2)

PRINT TAB(10); "Promezhutochnie rezul`tati"

PRINT " a b x1 x2 f(x1) f(x2) b-a" DO x1 = (a + b - e / 4) / 2 x2 = (a + b + e / 4) / 2 PRINT USING " ##.###### #.##### #.##### #.##### #.##### #.##### #.#####"; a; b; x1; x2; F(x1, LX1, LX2); F(x2, LX1, LX2); b - a IF F(x1, LX1, LX2) > F(x2, LX1, LX2) THEN a = x1 ELSE b = x2 LOOP UNTIL ABS(b - a) <= e

dihotom = (a + b) / 2

END FUNCTION

FUNCTION F (x, LX1, LX2)

F = LX1 * x ^ 2 + LX2 * x

END FUNCTION


5.2.3 Результат тестирования

 

 

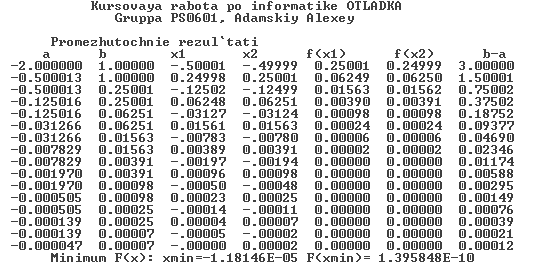
Модуль отработал верно. Минимум найден корректно.

5.3 Прогонка программы

Протестируем всю программу, задав 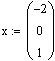 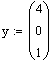 (тоже самое, что f(x)=x2)

x1=-1, x2=0. F(x)=L(x1)*x2+L(x2)*x, [a;b]=[-2;1].

Очевидно, что L(x1)=1, L(x2)=0, а минимум функции F(x) лежит в точке x=0

Cхемы алгоритмов других модулей совпадают с приведёнными в пп 5.1.1 и 5.2.1

5.3.1 Код программы при прогонке

DECLARE FUNCTION dihotom (a, b, e, LX1, LX2)

DECLARE FUNCTION LX (k, x(), y(), xl)

DECLARE FUNCTION F (xmin, LX1, LX2)

CLS

LOCATE 1, 15

PRINT "Kursovaya rabota po informatike OTLADKA"

LOCATE 2, 18

PRINT "Gruppa PS0601, Adamskiy Alexey"

PRINT

x(0) = -2: x(1) = 0: x(2) = 1

y(0) = 4: y(1) = 0: y(2) = 1

LX1 = LX(2, x(), y(), -1)

LX2 = LX(2, x(), y(), 0)

PRINT TAB(10); "Znacheniya polinoma Lagranzha v x1,x2"

PRINT TAB(15); "L(x1)="; LX1; "L(x2)="; LX2

PRINT

PRINT TAB(10); "Poisk minimuma F(x)"

xmin = dihotom(-2, 1, .0001, LX1, LX2)

PRINT TAB(10); "Minimum F(x): xmin="; xmin; "F(xmin)="; F(xmin, LX1, LX2)

END

FUNCTION dihotom (a, b, e, LX1, LX2)

PRINT TAB(10); "Promezhutochnie rezul`tati"

PRINT " a b x1 x2 f(x1) f(x2) b-a" DO PRINT USING " ##.###### #.##### #.##### #.##### #.##### #.##### #.#####"; a; b; x1; x2; F(x1, LX1, LX2); F(x2, LX1, LX2); b - a x1 = (a + b - e / 4) / 2 x2 = (a + b + e / 4) / 2 IF F(x1, LX1, LX2) > F(x2, LX1, LX2) THEN a = x1 ELSE b = x2 LOOP UNTIL ABS(b - a) <= e

dihotom = (a + b) / 2

END FUNCTION

FUNCTION F (x, LX1, LX2)

F = LX1 * x ^ 2 + LX2 * x

END FUNCTION

FUNCTION LX (k, x(), y(), xl)

l = 0 FOR i = 0 TO k L1 = y(i) FOR j = 0 TO k IF i <> j THEN L1 = L1 * (xl - x(j)) / (x(i) - x(j)) NEXT j l = l + L1 NEXT i

LX = l

END FUNCTION

5.3.2 Результат прогонки программы

 

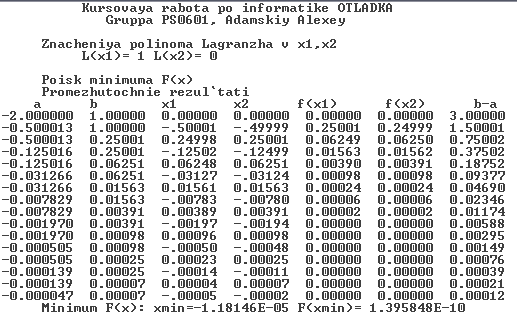
Программа отработала верно

Проверка результатов тестирования в среде MathCAD не требуется из-за очевидности полученных результатов.


6. Детализированная схема алгоритма

 




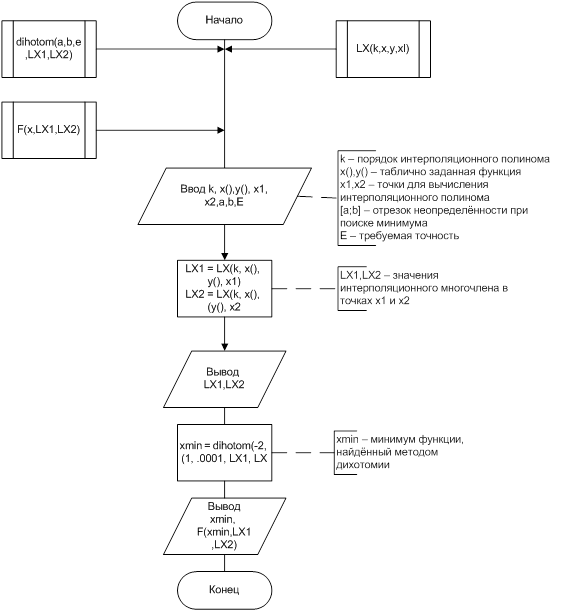
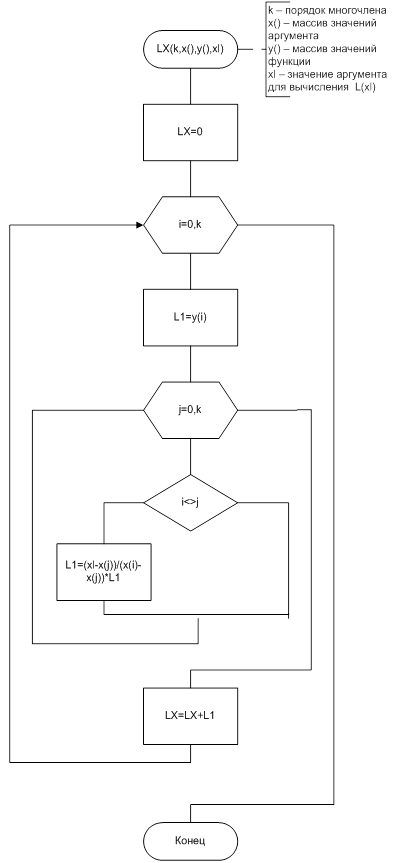
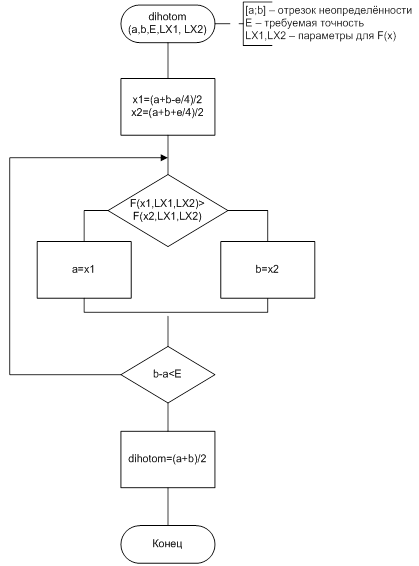
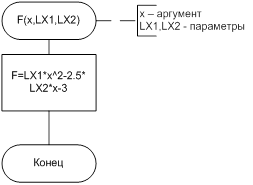
7. Код программы

 

DECLARE FUNCTION dihotom (a, b, E, LX1, LX2)

DECLARE FUNCTION LX (k, x(), y(), xl)

DECLARE FUNCTION F (xmin, LX1, LX2)

CLS

LOCATE 1, 15

PRINT "Kursovaya rabota po informatike"

LOCATE 2, 18

PRINT "Gruppa PS0601, Adamskiy Alexey"

PRINT

LOCATE 5, 18

INPUT "Vvedite k,a,b,x1,x2,E"; k, a, b, x1, x2, E

DIM x(0 TO k) AS SINGLE

DIM y(0 TO k) AS SINGLE

DATA 0,0.1, 0.2,0.3,0.4,0.5,0.6 FOR i = 0 TO k READ x(i) NEXT i

DATA 1.858652,1.851659,1.851401,1.848081,1.841914,1.833125,1.821948 FOR i = 0 TO k READ y(i) NEXT i

LX1 = LX(k, x(), y(), x1)

LX2 = LX(k, x(), y(), x2)

PRINT TAB(10); "Znacheniya polinoma Lagranzha v x1,x2"

PRINT TAB(15); "L(x1)="; LX1; "L(x2)="; LX2

PRINT

PRINT TAB(10); "Poisk minimuma F(x)"

xmin = dihotom(a, b, E, LX1, LX2)

PRINT TAB(10); "Minimum F(x): xmin="; xmin; "F(xmin)="; F(xmin, LX1, LX2)

END

FUNCTION dihotom (a, b, E, LX1, LX2)

PRINT TAB(10); "Promezhutochnie rezul`tati"

PRINT " a b x1 x2 f(x1) f(x2) b-a" DO x1 = (a + b - E / 1.3) / 2 x2 = (a + b + E / 1.3) / 2 PRINT USING " ##.###### #.##### #.##### #.##### #.##### #.##### #.#####"; a; b; x1; x2; F(x1, LX1, LX2); F(x2, LX1, LX2); b - a IF F(x1, LX1, LX2) > F(x2, LX1, LX2) THEN a = x1 ELSE b = x2 LOOP UNTIL b - a <= E

dihotom = (a + b) / 2

END FUNCTION

FUNCTION F (x, LX1, LX2)

F = LX1 * x ^ 2 - 2.5 * LX2 * x - 3

END FUNCTION

FUNCTION LX (k, x(), y(), xl)

l = 0 FOR i = 0 TO k L1 = y(i) FOR j = 0 TO k IF i <> j THEN L1 = L1 * (xl - x(j)) / (x(i) - x(j)) NEXT j l = l + L1 NEXT i

LX = l

END FUNCTION


8. Полученные результаты

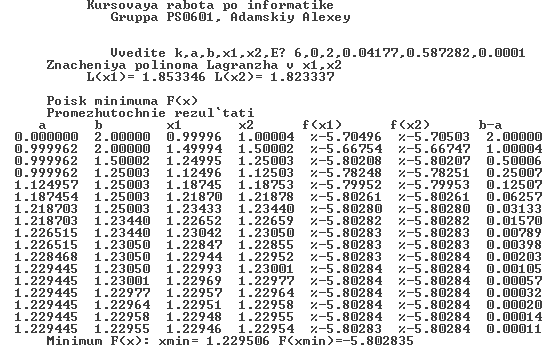
Выводы

1. Обоснованы и выбраны численные методы: - интерполяции таблично заданной функции с помощью полинома Лагранжа - одномерной оптимизации по методу дихотомии

2. Разработаны, протестированы модули, реализующие следующие методы: - поиск значений интерполяционного многочлена Лагранжа в требуемых точках (x1, x2) - поиск минимума функции F(x) с помощью метода дихотомии с требуемой точностью

3. Программа модульная, содержит следующие модули: - основной модуль, принимающий исходные данные, передающий их на обработку и выводящий конечный и промежуточный результаты - модуль поиска значений интерполяционного многочлена в точках x1 и x2 - модуль, задающий F(x) с параметрами LX1, LX2, найденными модулем интерполирования - модуль поиска минимума функции F(x) на отрезке [a;b] методом дихотомии

4. Получены следующие результаты: Полином Лагранжа L(x1)=1.853346, L(x2)=1.823337

Искомый минимум функции F(x) найден с точностью E=0.0001, xmin=1.229506

F(xmin)=-5.802835

5. Полученные результаты были проверены в MathCAD: Полученные в ходе работы программы результаты, очень хорошо согласуются с результатами, полученными в MathCAD, требуемая точность E=0.0001 соблюдалась, если научно подойти к выбору d в методе дихотомии.


Список литературы

1. Гловацкая А.П., Загвоздкина А.В., Кравченко О.М., Семёнова Т.И., Шакин В.Н: Практикум Численные методы и оптимизация по дисциплине «Информатика»

Москва, МТУСИ, 2004г.

2. А.П.Гловацкая: Конспект лекций «Информатика. Вычислительная математика» Москва, МТУСИ, 2006г.

3. Семёнова Т.И, Шакин В.Н.: Практикум Математический пакет MathCAD в дисциплине «Информатика», Москва, МТУСИ, 2006г.

4. А.В. Загвоздкина: Конспект лекций за 1 семестр 2007-2008 учебного года