Контрольная работа: Вычисление вероятности
1. Задача 1. В урне четыре белых и пять черных шаров. Из урны наугад вынимают два шара. Найти вероятность того, что один из этих шаров - белый, а другой - черный.
Решение.
Обозначим через А событие, состоящее в том, что один из этих шаров - белый, а другой - черный.
Вероятность события А найдем используя условную вероятность.
= 0,278
– вероятность того, что первый шар
белый. Вероятность вычислена по формуле классической вероятности.
– вероятность того, что второй шар
чнрный. Вероятность вычислена по формуле классической вероятности.
Ответ: 0,278.
2. Задача 2. Приведена схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны q1=0,1; q2=0,2; q3=0,3; q4=0,4; q5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.
Решение.
Пусть событие 
состоит в том, что сигнал
пройдет с входа на выход.
,
где 
– событие, состоящие в
том, что i-ый элемент находится в рабочем
состоянии.
Т.к. события - независимые совместные
события.
Ответ: 0,994.
3. Задача 3. На трех автоматических станках изготавливаются одинаковые детали. Известно, что 30% продукции производится первым станком, 25% - вторым и 45% - третьим. Вероятность изготовления детали, отвечающей стандарту, на первом станке равна 0,99 , на втором - 0,988 и на третьем - 0,98. Изготовленные в течение дня на трех станках нерассортированные детали находятся на складе. Определить вероятность того, что взятая наугад деталь не соответствует стандарту.
Решение. Событие А состоит в том, что что взятая наугад деталь не соответствует стандарту.
Гипотезы Н1, Н2, Н3.
– деталь изготовлена на первом
станке;
– деталь изготовлена на втором
станке;
– деталь изготовлена на третьем
станке;
Гипотезы Нi образуют полную группу событий.
Воспользуемся формулой полной вероятности:
– полная вероятность.
=
;
=
;
=
;
=
;
=0,45; 
=
;
Тогда
. = 0,015.
Ответ: 0,0,015.
4. Задача 4. Игральную кость подбрасывают 12 раз. Чему равно наивероятнейшее число выпадений 6?
Решение.
Найдем 
– наиболее вероятное число
выпадений 6.
Наивероятнейшее число определяют из двойного
неравенства:
;
– вероятность
появления события в каждом из 
независимых
испытаний. 
– вероятность того, что
при одном испытании выпадет 6 (по формуле классической вероятности). 
. 
– по условию.
;
Так как 
– целое число, то
наивероятнейшее число звонков равно 
.
Ответ: 2.
5. Задача 5. Дискретная
случайная величина 
может принимать
одно из пяти фиксированных значений 
, 
, 
, 
, 
с вероятностями 
, 
, 
, 
, 
соответственно. Вычислить
математическое ожидание и дисперсию величины .
Рассчитать и построить график функции распределения.
Решение.
Таблица 1.
|
|
1 | 4 | 5 | 7 | 8 |
|
|
0,3 | 0,3 | 0,1 | 0,15 | 0,15 |
Найдем числовые характеристики данного распределения.
Математическое ожидание
= 4,25
Дисперсию определим по
формуле: 
.
= 24,55.
Тогда 
Найдем функцию распределения случайной величины.
.
Построим график этой функции
6. Задача 6. Случайная
величина задана плотностью
вероятности
Определить константу 
, математическое ожидание,
дисперсию, функцию распределения величины ,
а также вероятность ее попадания в интервал [0;
]
Решение.
Коэффициент найдем используя свойство
функции плотности распределения: 
. Так
как функция плотности распределения принимает отличные от нуля значения на
интервале 
, то 
.
Вычислим определенный интеграл:
.
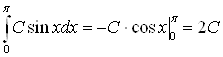Следовательно, 
, 
.
Математическое ожидание 
найдем по формуле:
.
Т.к. плотность
распределения принимает отличное от нуля значения только на отрезке [0, 
], то
= 
=
=
= 
.
Вычислили интеграл, используя формулу интегрирования по частям.
Найдем дисперсию 
, т.к. плотность
распределения принимает отличное от нуля значения только на отрезке
[0, ], то 
.
=
.
Найдем 
.
Воспользуемся формулой 
=
.
=
Найдем функцию распределения СВ Х.
При
. 
При
. 
При
. 
7. Задача 7. Случайная
величина распределена равномерно на
интервале 
. Построить график
случайной величины 
и определить
плотность вероятности 
.
Решение.
Найдем плотность
распределения случайной величины .
Случайная величина распределена
равномерно на интервале ,
поэтому на этом интервале 
, вне
этого интервала 
.
Построим график функции 
на интервале и в зависимости от числа
обратных функций выделим следующие интервалы:
;
;
Так как на интервалах 
и 
обратная функция не
существует, то для этих интервалов 
.
На интервале 
одна обратная функция 
, следовательно 
На интервале 
две обратных функции 
и 
, следовательно 
.
Найдем производные обратных функций
; 
.
Учитывая, что 
, получим
; 
.
В результате получим:
.
Таким образом, плотность
вероятности величины 
равна:
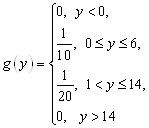
8. Задача 8. Двумерный
случайный вектор 
равномерно
распределен внутри области В. Двумерная плотность вероятности 
о любой точке этой области
В:
Вычислить коэффициент
корреляции между величинами 
и 
.
Решение.
Построим область 
Найдем значение константы
. Воспользуемся свойством
функции
Поскольку принимает отличные от нуля
значения внутри области , то
получим
= 
.
Следовательно, 
. Значит, 
Значение коэффициента корреляции вычислим по формуле
Корреляционный момент вычислим по формуле
.
.
.
.
Определим корреляционный момент
Ответ: 
9. Задача 9. По выборке одномерной случайной величины
1. Получить вариационный ряд;
2. Построить гистограмму равноинтервальным способом;
3. Построить гистограмму равновероятностным способом;
4. Вычислить оценки математического ожидания и дисперсии;
5.
Выдвинуть
гипотезу о законе распределения случайной величины и проверить ее при помощи
критерия согласия 
и критерия
Колмогорова (
)
| 0,22 | 0,42 | 0,07 | 1,69 | 0,42 | 0,94 | 1,81 | 2,24 | 0,74 | 0,75 |
| 0,80 | 2,59 | 0,55 | 0,43 | 0,51 | 0,38 | 1,41 | 0,73 | 0,03 | 0,96 |
| 0,63 | 0,17 | 0,10 | 0,09 | 1,09 | 1,52 | 2,97 | 0,91 | 1,53 | 0,55 |
| 1,23 | 1,27 | 0,75 | 1,55 | 0,88 | 0,57 | 0,31 | 1,04 | 1,71 | 1,39 |
| 1,16 | 0,86 | 1,13 | 0,82 | 2,02 | 1,17 | 0,25 | 0,64 | 0,07 | 0,11 |
| 1,99 | 0,71 | 2,17 | 0,23 | 2,68 | 1,82 | 1,19 | 0,05 | 1,23 | 4,70 |
| 0,37 | 0,40 | 1,31 | 0,20 | 0,50 | 2,48 | 0,32 | 1,41 | 0,23 | 1,27 |
| 0,33 | 1,48 | 0,52 | 0,68 | 0,30 | 0,40 | 0,24 | 1,52 | 0,17 | 0,17 |
| 0,83 | 1,20 | 0,65 | 0,05 | 1,45 | 0,23 | 0,37 | 0,09 | 3,66 | 0,28 |
| 0,77 | 0,11 | 1,95 | 0,10 | 0,95 | 0,65 | 4,06 | 3,16 | 0,51 | 2,02 |
Решение.
Найдем размах вариации 
. 
0,03; 
4,70;
4,70–0,03 = 4,67.
Вариационный ряд распределения имеет вид:
|
|
|
|
|
| 0,03 | 1 | 0,86 | 1 |
| 0,05 | 2 | 0,88 | 1 |
| 0,07 | 2 | 0,91 | 1 |
| 0,09 | 2 | 0,94 | 1 |
| 0,1 | 2 | 0,95 | 1 |
| 0,11 | 2 | 0,96 | 1 |
| 0,17 | 3 | 1,04 | 1 |
| 0,2 | 1 | 1,09 | 1 |
| 0,22 | 1 | 1,13 | 1 |
| 0,23 | 3 | 1,16 | 1 |
| 0,24 | 1 | 1,17 | 1 |
| 0,25 | 1 | 1,19 | 1 |
| 0,28 | 1 | 1,2 | 1 |
| 0,3 | 1 | 1,23 | 2 |
| 0,31 | 1 | 1,27 | 2 |
| 0,32 | 1 | 1,31 | 1 |
| 0,33 | 1 | 1,39 | 1 |
| 0,37 | 2 | 1,41 | 2 |
| 0,38 | 1 | 1,45 | 1 |
| 0,4 | 2 | 1,48 | 1 |
| 0,42 | 2 | 1,52 | 2 |
| 0,43 | 1 | 1,53 | 1 |
| 0,5 | 1 | 1,55 | 1 |
| 0,51 | 2 | 1,69 | 1 |
| 0,52 | 1 | 1,71 | 1 |
| 0,55 | 2 | 1,81 | 1 |
| 0,57 | 1 | 1,82 | 1 |
| 0,63 | 1 | 1,95 | 1 |
| 0,64 | 1 | 1,99 | 1 |
| 0,65 | 2 | 2,02 | 2 |
| 0,68 | 1 | 2,17 | 1 |
| 0,71 | 1 | 2,24 | 1 |
| 0,73 | 1 | 2,48 | 1 |
| 0,74 | 1 | 2,59 | 1 |
| 0,75 | 2 | 2,68 | 1 |
| 0,77 | 1 | 2,97 | 1 |
| 0,8 | 1 | 3,16 | 1 |
| 0,82 | 1 | 3,66 | 1 |
| 0,83 | 1 | 4,06 | 1 |
| 4,7 | 1 |
Построим гистограмму равноинтервальным способом. Число интервалов рассчитаем по формуле 
. Длина
частичного интервала вычисляется по формуле
.
Полученные значения запишем в таблицу
| № |
|
|
|
|
|
|
| 1 | 0,03 | 0,497 | 0,467 | 34 | 0,34 | 0,73 |
| 2 | 0,497 | 0,964 | 0,467 | 27 | 0,27 | 0,58 |
| 3 | 0,964 | 1,431 | 0,467 | 15 | 0,15 | 0,32 |
| 4 | 1,431 | 1,898 | 0,467 | 10 | 0,1 | 0,21 |
| 5 | 1,898 | 2,365 | 0,467 | 6 | 0,06 | 0,13 |
| 6 | 2,365 | 2,832 | 0,467 | 3 | 0,03 | 0,06 |
| 7 | 2,832 | 3,299 | 0,467 | 2 | 0,02 | 0,04 |
| 8 | 3,299 | 3,766 | 0,467 | 1 | 0,01 | 0,02 |
| 9 | 3,766 | 4,233 | 0,467 | 1 | 0,01 | 0,02 |
| 10 | 4,233 | 4,7 | 0,467 | 1 | 0,01 | 0,02 |
Равноинтервальная гистограмма имеет вид:
Построим гистограмму равновероятностным способом.
| № |
|
|
|
|
|
|
| 1 | 0,03 | 0,17 | 0,14 | 10 | 0,1 | 0,7143 |
| 2 | 0,17 | 0,25 | 0,08 | 10 | 0,1 | 1,2500 |
| 3 | 0,25 | 0,42 | 0,17 | 10 | 0,1 | 0,5882 |
| 4 | 0,42 | 0,57 | 0,15 | 10 | 0,1 | 0,6667 |
| 5 | 0,57 | 0,77 | 0,2 | 10 | 0,1 | 0,5000 |
| 6 | 0,77 | 0,96 | 0,19 | 10 | 0,1 | 0,5263 |
| 7 | 0,96 | 1,27 | 0,31 | 10 | 0,1 | 0,3226 |
| 8 | 1,27 | 1,53 | 0,26 | 10 | 0,1 | 0,3846 |
| 9 | 1,53 | 2,17 | 0,64 | 10 | 0,1 | 0,1563 |
| 10 | 2,17 | 4,7 | 2,53 | 10 | 0,1 | 0,0395 |
Равновероятностная гистограмма имеет вид:
Оценку математического ожидания вычислим по формуле
1,00.
Оценку дисперсии вычислим по формуле:
, 
0,82,
Построим доверительный интервал для математического ожидания при неизвестной дисперсии:
В нашем случае
1,00, 
0,82,
, 
, 
.
; 
Доверительный интервал
для математического ожидания 
.
Доверительный интервал для дисперсии
, 
=1,96 (
).
По виду равноинтервальной гистограммы выдвигаем гипотезу о том, что случайная величина X распределена по показательному закону:
H0 : 
H1 : 
Определим оценку
неизвестного параметра 
Предполагаемый закон
распределения 
. Найдем
вероятности попадания в каждый из интервалов
Теоретические частоты найдем по формуле
| № |
Интервалы [xi; xi+1) |
|
|
|
|
|
|
| 1 | 0,03 | 0,497 | 0,36 | 36,00 | -2,00 | 4,00 | 0,1111 |
| 2 | 0,497 | 0,964 | 0,23 | 23,00 | 4,00 | 16,00 | 0,6957 |
| 3 | 0,964 | 1,431 | 0,14 | 14,00 | 1,00 | 1,00 | 0,0714 |
| 4 | 1,431 | 1,898 | 0,09 | 9,00 | 1,00 | 1,00 | 0,1111 |
| 5 | 1,898 | 2,365 | 0,06 | 6,00 | 0,00 | 0,00 | 0,0000 |
| 6 | 2,365 | 2,832 | 0,04 | 4,00 | -1,00 | 1,00 | 0,2500 |
| 7 | 2,832 | 3,299 | 0,02 | 2,00 | 0,00 | 0,00 | 0,0000 |
| 8 | 3,299 | 3,766 | 0,01 | 1,00 | 0,00 | 0,00 | 0,0000 |
| 9 | 3,766 | 4,233 | 0,01 | 1,00 | 0,00 | 0,00 | 0,0000 |
| 10 | 4,233 | 4,7 | 0,01 | 1,00 | 0,00 | 0,00 | 0,0000 |
|
|
1,24 |
НАБЛ=Число степеней свободы 
определяют по формуле 
. По таблице критерия
Пирсона находим: 
. Так как 
, то нет оснований
отвергать гипотезу о показательном распределении. Проверим гипотезу о
показательном распределении с помощью -критерия
Колмогорова. Теоретическая функция распределения F0(x)
показательного закона равна
Проверим гипотезу о
нормальном распределении с помощью -критерия
Колмогорова. Все вспомогательные расчеты сведем в таблицу.
| № |
Интервалы [xi; xi+1) |
частота в интервале
|
|
|
|
|
| 1 | -2,951 | 7 | 34 | 0,34 | 0,36 | 0,02 |
| 2 | -2,513 | 10 | 27 | 0,61 | 0,59 | 0,02 |
| 3 | -2,075 | 8 | 15 | 0,76 | 0,73 | 0,03 |
| 4 | -1,637 | 12 | 10 | 0,86 | 0,82 | 0,04 |
| 5 | -1,199 | 14 | 6 | 0,92 | 0,88 | 0,04 |
| 6 | -0,761 | 11 | 3 | 0,95 | 0,91 | 0,04 |
| 7 | -0,323 | 9 | 2 | 0,97 | 0,93 | 0,04 |
| 8 | 0,115 | 4 | 1 | 0,98 | 0,95 | 0,03 |
| 9 | 0,553 | 16 | 1 | 0,99 | 0,96 | 0,03 |
| 10 | 0,991 | 9 | 1 | 1,00 | 0,97 | 0,03 |
; 
.
То таблице квантилей
распределения Колмогорова по уровню значимости 
находим
критическое значение 
.
Так как 
, то нет оснований
отвергать гипотезу о нормальном распределении.
10. Задача 10. По выборке двумерной случайной величины
1. Вычислить оценку коэффициента корреляции;
2.
Вычислить
параметры линии регрессии 
и 
;
3. Построить диаграмму рассеивания и линию регрессии;
Решение
Найдем числовые
характеристики величин и .
0,88; 
0,10.
1,59; 
.
1,76; 
.
Корреляционный момент равен:
–0,23
Найдем уравнения
регрессии 
где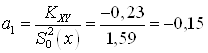 
; 
Уравнение регрессии имеет вид:
.
Коэффициент корреляции равен:
.
Найдем интервальную оценку.
.
,
Проверим гипотезу об
отсутствии корреляционной зависимости 
.
Проверим нулевую гипотезу
: о равенстве нулю
генерального коэффициента корреляции, при конкурирующей гипотезе 
.
.
По таблице критических
точек распределения Стьюдента, по заданному уровню и
числу степеней свободы 
найдем
критическую точку 
двусторонней
критической области. 
.
Так как 
– нулевую гипотезу
принимаем.
| Зависимость количества лейкоцитов в крови человека от уровня радиации | |
|
Overview vichislenia diagrammi Гист1 Гист2 regress KorrelTabl Лист1 Лист2 Gipoteza Sheet 1: vichislenia X Y M(X)= 1.47 x*x y*y x*x*x y*y*y X для цм3 Y ... Законами распределения непрерывных случайных величин называют плотности распределений. Для определения дисперсии необходимо ввести понятие отклонения случайной величины от ее математического ожидания. |
Раздел: Рефераты по медицине Тип: реферат |
| Инновационный менеджмент (учебник) | |
|
ИННОВАЦИОННЫЙ МЕНЕДЖМЕНТ УЧЕБНИК под редакцией Действительного члена международной Академии информатизации, доктора экономических наук, профессора ... В малой выборке дисперсия генеральной совокупности неизвестна, поэтому для ее оценки используется дисперсия малой выборки (2). Для оценки параметров генеральной совокупности по ... Вероятность безотказной работы характеризует вероятность отсутствия отказов при заданных условиях эксплуатации в течение определенного заданного интервала времени: |
Раздел: Рефераты по менеджменту Тип: реферат |
| Первичная статистическая обработка информации | |
|
400 45 431 394 362 436 343 403 483 462 395 467 420 411 391 397 455 412 363 449 439 411 468 435 313 486 463 417 369 377 409 390 389 386 409 379 412 370 ... Вычислить точечные и интервальные оценки математического ожидания и дисперсии (с.к.о.) по данным таблицы 1 при доверительной вероятности 0,95. На графиках гистограммы и эмпирической функции распределения (рис.1,3) построим сглаживающие функции (теоретические кривые) плотности вероятности и функции распределения в ... |
Раздел: Рефераты по математике Тип: реферат |
| Процесс и критерии проверки статистических гипотез | |
|
Содержание Введение Глава 1. Общие понятия проверки статистических гипотез 1.1 Сущность и виды проверки статистических гипотез 1.2 Выбор критериев для ... Суть его сводится к выбору такого критерия К с известной функцией плотности f(k) при условии справедливости гипотезы Н0, чтобы при заданном условии значимости можно было бы найти ... Например, проверка гипотезы о виде закона распределения случайной величины может быть осуществлена с помощью критерия согласия Пирсона 2; проверка гипотезы о равенстве неизвестных ... |
Раздел: Рефераты по экономике Тип: курсовая работа |
| Теория вероятностей и математическая статистика | |
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования "Южный ... Проведя первичную обработку статистических данных , вычислив по этим данным значения точечных оценок числовых характеристик, мы выдвигаем предположения - гипотезы о виде закона ... будет плотностью вероятности случайной величины x. Найти функцию распределения F(x), математическое ожидание Мx. |
Раздел: Рефераты по математике Тип: учебное пособие |