Дипломная работа: Произведения конечных групп, близких к нильпотентным

Изучение групп, представимых в произведение своих подгрупп является классической задачей алгебры.

Изучение факторизуемых групп началось с изучения групп, разложимых в прямое произведение некоторого множества своих истинных подгрупп, т.е. при условиях, когда факторизующие подгруппы инвариантны в факторизуемой группе и пересечение любой из них с произведением остальных равно единице. Еще в XIX веке было установлено, что любая конечная абелева группа разложима в произведение некоторого множества циклических подгрупп (Фробениус и Штикельбергер [1]). В связи с этой теоремой в теорию групп пришел вопрос о конечных неабелевых группах, факторизуемых некоторым множеством своих попарно перестановочных циклических подгрупп. При этом не предлагается ни нормальность факторизующих множителей, ни единичность пересечения каждого из них с произведением остальных. Был установлен ряд свойств конечных групп, имеющих факторизацию такого рода, в частности их сверхразрешимость (теорема Хупперта [2]).

Как известно, конечная нильпотентная группа – это прямое произведение -подгрупп по разным простым  В связи с этим возник вопрос характеризации конечных групп, разложимых в произведение попарно перестановочных -подгрупп по разным простым

Случай, когда группа является произведением своих двух силовских подгрупп, т.е. бипримарной, был рассмотрен еще Берсайдом, который установил их разрешимость. В 1938 году Ф. Холл[28] доказал свою знаменитую теорему о том, что конечная группа тогда и только тогда разложима в произведение попарно перестановочных -подгрупп по разным простым , когда она разрешима.

В связи с этими результатами возник вопрос о строении конечных групп, представимых в произведение своих нильпотентных подгрупп. Ответ на этот вопрос был получен Виландтом[4] и Кегелем[19], которые установили разрешимость таких групп.

Класс конечных групп, представимых в произведение своих двух некоторых нильпотентных подгрупп (кратко, динильпотентных групп) достаточно сложен. Он включает в себя сверхразрешимые группы, бипримарные, метанильпотентные и т.д. и этими примерами он далеко не исчерпывается.

Даже для таких групп связь группы со свойствами подгрупп-множителей достаточно сложная и исследование ее становится весьма непростой задачей.

В последние пятнадцать лет эта связь изучалась в работах многих авторов. Получено немало интересных глубоких результатов и разработаны методы исследования. Естественно, что это направление далеко не исчерпало себя и имеет широкие перспективы.

Настоящая дипломная работа посвящена изучению некоторых свойств конечных разрешимых групп, представимых в виде произведения своих двух -разложимых подгрупп. В дальнейшем, для краткости, группы с таким свойством буем называть ди--разложимые. Рассматриваются только конечные разрешимые группы.

Работа состоит из перечня условных обозначений, реферата, введения, основной части, включающей три раздела, заключения и списка цитируемой литературы.

Первый раздел носит справочный характер. Здесь приведены обозначения, определения и некоторые известные результаты, существенно используемые в работе.

Второй раздел посвящен изложению некоторых результатов о строении групп ди--разложимых групп. Здесь собраны из различных источников и систематизированы основные результаты о ди--разложимых группах и получен один новый результат.

Напомним следующее определение:

2.2.1 О п р е д е л е н и е. Пусть  – непустая формация. Подгруппа  группы  называется:

1) -субнормальной в , если либо , либо существует максимальная цепь подгрупп  такая, что  для всех  (обозначается );

2) -достижимой в , если существует цепь подгрупп  такая, что либо подгруппа  субнормальна в , либо  для любого  (oбозначается ).

2.2.6 Т е о р е м а. Пусть  – наслественная насыщенная формация, причем  и  – ди--разожимая группа. Тога справиливы следующие утверждения:

1) если   и  то

2) если   и  то

Основные результаты и выводы работы сосредоточены в третьем разделе, в котором изучаются свойства подгрупп ди--разложимых групп.

В 1958 году Виландт [4] ввел следующее понятие. Подгруппа  группы  называется факторизуемой относительно  если  и  Хайнекен Н. [4] в 1990 году исследовал факторизуемые -проекторы в динильпотентных конечных группах для случая, когда  – насыщенная формация. Группа  называется динильпотентной, если , где  и  – нильпотентные подгруппы группы  Подробнее в 1994 году Амберг В. и Хёфлинг В. [3] распространили основной результат Хайнекена на классы Шунка.

В третьем разделе нами исследуются факторизуемые проекторы в ди--нильпотентных группах. В классе всех конечных разрешимых групп получены следующие результаты.

3.2.1 Т е о р е м а. Пусть  – некоторое множество простых чисел,  – класс Шунка и . Если  – ди--разложимая группа, причем , то в  имеется хотя бы один факторизуемый относительно  -проектор.

Так как всякая насыщенная формация является классом Шунка, то справедливо следующее:

3.2.2 С л е д с т в и е. Пусть  – насыщенная формация, причем  Если  – ди--разложимая группа, причем , то в  имеется хотя бы один факторизуемый относительно  -проектор.

Следуя [], подгруппу  группы  назовем -картеровой подгруппой, если  -нильпотентна,  и  содержит некоторую -холловскую подгруппу группы .

3.2.4 С л е д с т в и е. Пусть  – ди--разложимая группа. Тогда в  имеется хотя бы одна факторизуемая относительно  -картерова подгруппа.

Следуя, [] подгруппу  группы  назовем -гашюцевой подгруппой, если  -сверхразрешима, содержит некоторую -холловскую подгруппу группы  и для  индекс  есть составное число.

3.2.6 С л е д с т в и е. Пусть  – ди--разложимая группа. Тогда в  имеется хотя бы одна факторизуемая относительно  -гашюцева подгруппа.

Цель дипломной работы – изучение основных свойств конечных разрешимых произведений -разложимых групп и их факторизуемых подгрупп. В работе решены следующие задачи: – изучены свойства примитивных конечных разрешимых произведений -разложимых групп; – найдены условия факторизуемости -проекторов конечных разрешимых произведений -разложимых групп для случая, когда  – класс Шунка конечных разрешимых групп; – найдены приложения полученных результатов для классических формаций.

Объектом исследования являются конечные разрешимые произведения -разложимых групп и их подгрупп. Предметом исследования – свойства конечных разрешимых произведений -разложимых групп и их подгрупп.

Методология и методы исследования. В дипломной работе используются методы доказательств абстрактной теории конечных групп, а также методы теории классов конечных групп.

Новизна полученных результатов: Результаты первых двух разделов носят в основном реферативный характер. Теорема 2.2.6 является новой. Параграф 3.1 раздела 3 взят из работы Васильевой Т.И. [36]. Параграф 3.2 содержит новые результаты.

Практическое применение и экономическая значимость работы: Результаты дипломной работы могут быть использованы в научно-исследовательской работе студентов, аспирантов, а также в учебном процессе при чтении спецкурсов на математических специальностях в высших учебных заведениях.

Необходимые сведения

Перечень определений и условных обозначений

Рассматриваются только конечные группы. Ниже мы приводим известные определения и понятия, которые существенно используются в работе.

 – простое число;

 – группа;

 – класс групп;

 – некоторое множество простых чисел;

 – дополнение к  во множестве всех простых чисел;

 – множество всех различных простых делителей порядка группы G;

 – множество всех различных простых делителей порядков групп, которые принадлежат ;

 – формация;

 – класс всех нильпотентных групп;

 – класс всех нильпотентных -групп;

 – класс всех нильпотентных -групп;

1.1.1 О п р е д е л е н и е. Подгруппа  группы  называется факторизуемой относительно  если  и

1.1.2 О п р е д е л е н и е. Группа  называется динильпотентной, если  где  и  – нильпотентные подгруппы группы

1.1.3 О п р е д е л е н и е. Группа называется сверхразрешимой, если она обладает нормальным рядом с циклическими факторами.

1.1.4 О п р е д е л е н и е. Холловой подгруппой конечной группы называют подгруппу, порядок и индекс которой взаимно просты.

1.1.5 О п р е д е л е н и е. Минимальной нормальной подгруппой группы  называется нормальная подгруппа  группы  такая, что  и в  нет нетривиальных нормальных подгрупп группы

1.1.6 О п р е д е л е н и е. Произведение всех нормальных нильпотентных подгрупп группы  называется подгруппой Фиттинга группы . Обозначается через

1.1.7 О п р е д е л е н и е. Группа  дисперсивна, если она обладает нормальным рядом, факторы которого изоморфны силовким подгруппам.

1.1.8 О п р е д е л е н и е. Формацией называется класс групп, замкнутый относительно факторгрупп и подпрямых произведений.

1.1.9 О п р е д е л е н и е. Формация называется насыщенной, если она является насыщенным классом, т.е. если   то

1.1.10 О п р е д е л е н и е. Класс  называется примитивно замкнутым классом, если все примитивные факторгруппы группы  принадлежат , то

1.1.11 О п р е д е л е н и е. Классом Шунка называется класс групп, который одновременно замкнут относительно факторгрупп и является примитивно замкнутым классом.

1.1.12 О п р е д е л е н и е. Если  – подгруппа группы  и  то  называется -подгруппой.

1.1.13 О п р е д е л е н и е. -максимальной подгруппой группы  называется такая -подгруппа  группы  которая не содержится ни в какой большей -подгруппе.

1.1.14 О п р е д е л е н и е. Пусть  – некоторый класс групп. Подгруппа  группы  называется -проектором, если выполнены условия:  и из того, что , а , всегда следует

1.1.15 О п р е д е л е н и е. Подгруппу  группы  назовем -картеровой подгруппой, если  -нильпотентна,  и  содержит некоторую -холловскую подгруппу группы .

1.1.16 О п р е д е л е н и е. Подгруппу  группы  назовем -гашюцевой подгруппой, если  -сверхразрешима, содержит некоторую -холловскую подгруппу группы  и для  индекс  есть составное число.

1.1.17 О п р е д е л е н и е. Пересечение всех нормальных подгрупп группы  факторгруппы по которым принадлежат  обозначают через  и называют -корадикалом группы

1.1.18 О п р е д е л е н и е. -класс Шунка – класс Шунка, для которого из условия , всегда следует .

Факторизуемые подгруппы произведений конечных групп

В настоящем разделе излагается подробно теория факторизуемых подгрупп теории конечных групп, взятая из [32] c точными ссылками на работы авторов приведенных результатов.

1.2.1 Л е м м а. Пусть  – некоторая группа,  и  – ее подгруппы. Подгруппы  и  перестановочны тогда и только тогда, когда произведение  является подгруппой группы .

(Говорят, что непустые множества  и  элементов группы перестановочны, если .)

Д о к а з а т е л ь с т в о. Необходимость. Пусть подгруппы  и  перестановочны. Тогда, очевидно

 (Если  – непустое множество элементов некоторой группы, то, как обычно, .)

С учетом последних соотношений множество  является подгруппой группы .

Достаточность. Пусть подмножество  является подгруппой. Тогда, очевидно,  т.е. подгруппы  и  перестановочны.

Лемма доказана.

1.2.2 О п р е д е л е н и е. Пусть  – группа, факторизуемая двумя подгруппами  и . Если , то будем говорить, что подгруппа  факторизуема относительно разложения

1.2.3 Л е м м а (Виландт[4]). Пусть  – группа, факторизуемая двумя подгруппами  и ;  – некоторая подгруппа группы  и  – нормализатор подгруппы  в . Подгруппа  факторизуема относительно разложения  если выполняется следующее условие:

(*) всякий раз, когда для элементов  и

элементы  и  содержатся в .

Д о к а з а т е л ь с т в о. Пусть выполняется условие (*),  и  – произвольные элементы соответственно из  и , для которых . Тогда выполняется соотношение (1) и, следовательно,  и  Поэтому ввиду произвольности элементов  и   и, значит, . Лемма доказана.

1.2.4 Л е м м а. Пусть  – группа, факторизуемая двумя подгруппами  и ;  – подгруппа, порожденная некоторыми инвариантными подгруппами соответственно групп   и  и  – нормализатор подгруппы  в . Подгруппа  факторизуема относительно разложения  тогда и только тогда, когда выполняется условие (*) из формулировки леммы 1.2.3.

Д о к а з а т е л ь с т в о. Если условие (*) выполняется, то по лемме 1.2.3 подгруппа  факторизуема относительно разложения  Пусть подгруппа  факторизуема относительно разложения   и  – какие-нибудь элементы соответственно из подгрупп  и , такие, что выполняется соотношение (1). Поскольку  то для некоторых элементов  и  Отсюда получаем

Очевидно,  Поэтому с учетом соотношений (2)  и  Лемма доказана.

1.2.5 Л е м м а. Пусть  – группа,  – ее подгруппа и  – элемент группы  некоторая натуральная степень которого содержится в . Тогда подгруппа  не является истинной подгруппой группы .

(Подгруппа, отличная от самой группы, называется ее истинной подгруппой.)

Д о к а з а т е л ь с т в о. Действительно, если бы  была истинной подгруппой группы , то она, как легко убедиться, была бы и истинной подгруппой группы  при любом натуральном , в том числе при , для которого , что невозможно. Лемма доказана.

1.2.6 Л е м м а. Пусть  – группа, факторизуемая двумя подгруппами  и  Пусть, далее  – некоторые инвариантные подгруппы соответственно групп   – подгруппа, порожденная подгруппами  и  – нормализатор подгруппы  в  Подгруппа  факторизуема относительно разложения  если выполняется хотя бы одно из следующих условий:

1) ни для какого элемента  подгруппа  не является истинной подгруппой группы

2) ни для какого элемента  подгруппа  не является истинной подгруппой группы

3) подгруппа  не изоморфна ни одной из своих истинных подгрупп (в частности, конечна;)

4) по крайней мере одна из фактор-групп  и  периодическая.

1.2.7 Л е м м а (Дедекинд). Пусть  – подгруппа группы  и  – подгруппа из . Тогда для любой подгруппы  группы  выполняется соотношение

Д о к а з а т е л ь с т в о. Пусть  и  – произвольные элементы соответственно подгрупп  и . Тогда  и  и, значит, . Следовательно,  С другой стороны, если  для некоторых элементов  и  то  и, значит,  Следовательно,  Итак, соотношение (3) выполняется. Лемма доказана.

1.2.8 Л е м м а (С.Н. Черников [17]). Пусть  – группа, факторизуемая двумя подгруппами  и , и  – подгруппа группы , содержащая . Тогда

1.2.9 Л е м м а (Сесекин [18]). Пусть  – группа, факторизуемая двумя подгруппами  и ;  – некоторая инвариантная подгруппа группы   и  Тогда выполняются соотношения

Д о к а з а т е л ь с т в о. Учитывая, что  и  и используя лемму 1.2.7, получаем

Покажем, что  Так как  и , то  Пусть  – произвольный элемент из  и  где  и  Тогда  значит,  Поэтому ввиду произвольности   Следовательно, с учетом соотношений (5)  и, значит,  Таким образом, все соотношения (4) выполняются. Лемма доказана.

1.2.10 Л е м м а. Пусть  – группа, разложимая в произведения

некоторых подгрупп  и  и конечной подгруппы . Тогда индексы подгруппы  в группах ,  и  конечны и выполняются соотношения

Д о к а з а т е л ь с т в о. С учетом соотношений (6), очевидно,

Поэтому

Лемма доказана.

1.2.11 Л е м м а. Пусть  – группа, факторизуемая двумя подгруппами  и  пересечение которых периодическое, и  – локально конечная подгруппа группы  порожденная некоторым множеством конечных инвариантных подгрупп группы  и  Тогда

1.2.12 Л е м м а. Пусть  – группа, факторизуемая двумя подгруппами  и ;  – конечная подгруппа группы , порожденная некоторыми инвариантными подгруппами групп   и  и  – нормализатор подгруппы  в . Тогда найдутся, перестановочные подгруппы  и  каждая из которых может быть порождена не более чем  элементами, такие, что

Примечание. В случаях, когда подгруппа  инвариантна в  и когда она порождена некоторой инвариантной подгруппой группы  и некоторой инвариантной подгруппой группы , существование перестановочных подгрупп  и  каждая из которых порождена не более чем  элементами, таких, что  установил Кегель [19] (см. в [19] лемму 1.3 и ее доказательство.)

1.2.13 Л е м м а (Амберг [20]). Пусть  – группа, факторизуемая двумя подгруппами  и   и  – некоторые подгруппы конечных индексов соответственно групп  и   – подгруппа, порожденная  и  Тогда индекс подгруппы  в  конечен.

1.2.14 Л е м м а (Амберг [21]). Пусть  – группа, факторизуемая двумя подгруппами  и  с конечными фактор-группами  и  Тогда фактор-группа  конечна и

1.2.15 С л е д с т в и е. Пусть  – группа, факторизуемая  попарно перестановочными подгруппами ,  с конечными фактор-группами  Тогда фактор-группа  конечна и .

1.2.16 Л е м м а. Пусть  – группа, факторизуемая двумя подгруппами  и   и  – некоторые непустые инвариантные множества элементов соответственно групп  и  Тогда для любых элементов  и  группы  найдется такой ее элемент  что  и

1.2.17 Л е м м а (Виландт [16]). Пусть  – группа, факторизуемая двумя подгруппами  и  Тогда для любых элементов  и  группы  во-первых, найдется такой ее элемент  что  и  и, во-вторых, выполняется соотношение

1.2.18 Л е м м а (Виландт [16]). Пусть  – группа, факторизуемая двумя подгруппами  и   – некоторая подгруппа группы  Следующие условия равносильны:

1) подгруппа  факторизуема относительно разложения  и содержит пересечение

2) каковы бы ни были элементы  и  произведение  содержится в  в том и только том случае, когда элементы  и  содержатся в

Д о к а з а т е л ь с т в о. Пусть выполняется условие 1). Покажем, что выполняется условие 2).

Пусть  и  – элементы, для которых  Так как подгруппа  факторизуема относительно разложения  то  для некоторых элементов  и  Отсюда получаем

и

Итак, при условии 1) выполняется условие 2). Обратное очевидно. Лемма доказана.

1.2.19 С л е д с т в и е. Пусть  – группа, факторизуемая двумя подгруппами  и   – подгруппа группы  содержащая пересечение  и факторизуемая относительно разложения   и  – некоторые подгруппы соответственно групп  и  содержащие пересечение  При этих условиях подгруппа  факторизуема подгруппами  и  тогда и только тогда, когда  и

1.2.20 Л е м м а (Амберг [20]). Пусть  – группа, факторизуема двумя подгруппами  и . Тогда пересечение произвольной совокупности подгрупп группы , факторизуемых относительно разложения  и содержащих пересечение , является подгруппой, факторизуемой относительно этого разложения.

Д о к а з а т е л ь с т в о. Пусть  – факторизуемые относительно разложения  подгруппы группы , каждая из которых содержит пересечение  Если для некоторых элементов  и  произведение  содержится в  то оно содержится и в каждой подгруппе Поэтому ввиду леммы 1.2.11 элементы  и  содержатся в каждой подгруппе  и, значит, в  Следовательно, снова ввиду леммы 1.2.11 подгруппа  факторизуема относительно разложения  Лемма доказана.

1.2.21 Л е м м а (Амберг [20]). Пусть  – группа, факторизуемая двумя подгруппами  и   – ее подгруппа, факторизуемая относительно разложения  и содержащая пересечение  Тогда

Д о к а з а т е л ь с т в о. Пусть  – произвольный элемент множества  Тогда  для некоторых элементов  и  Отсюда  Так как произведение  принадлежит  и  содержит пересечение  то ввиду леммы 1.2.11  Поэтому элемент  принадлежит  Таким образом,  следовательно, соотношение (4) выполняется. Лемма доказана.

1.2.22 Л е м м а (Амберг [20]). Пусть  – группа, факторизуемая двумя подгруппами  и   – некоторая подгруппа группы  перестановочная с подгруппами  и   – пересечение всех подгрупп группы  факторизуемых относительно разложения  и содержащих подгруппы  и   и  Тогда выполняются соотношения

1.2.23 Л е м м а. Пусть  – группа, факторизуемая двумя подгруппами  и   – некоторая подгруппа группы   – пересечение всех подгрупп группы  факторизуемых относительно разложения  и содержащих подгруппы  и  Пусть для некоторой подгруппы  факторизуемой относительно разложения  и содержащей подгруппы  и  подгруппа  перестановочна с подгруппами  и  Тогда выполняются соотношения

1.2.24 Л е м м а (Чунихин [22]). Пусть  – группа, факторизуемая двумя подгруппами  и ;  – инвариантная подгруппа группы , содержащаяся в пересечении  Тогда нормальное замыкание подгруппы  в  совпадает с ее нормальным замыканием в

1.2.25 Л е м м а (Виландт [23], Хупперт [24], гл. IV, предложение 4.6). Пусть  – группа, факторизуемая двумя подгруппами  и ;  – непустое множество простых чисел. Тогда если в группах  и  силовские -подгруппы сопряжены (в часности, если  состоит из одного простого числа), то найдутся силовские и одновременно холловы -подгруппы  и  соответственно групп  и  такие, что

1.2.26 Л е м м а (Н.С. Черников [25], Зайцев [26]). Пусть  – конечная группа, факторизуемая двумя подгруппами  и ;  и  – некоторые подгруппы соответственно групп  и   – подгруппа, порожденная подгруппами  и  Тогда выполняется следующее неравенство для индексов:

1.2.27 Л е м м а (Виландт [23]). Пусть  – конечная группа, факторизуемая  попарно перестановочными нильпотентными подгруппами   Если произведение каждых двух подгрупп  является разрешимой группой, то группа  разрешима.

1.2.28 Л е м м а. Пусть группа  факторизуема двумя подгруппами – инвариантной подгруппой  и некоторой подгруппой   – непустое множество элементов подгруппы  такое, что  Тогда выполняются соотношения

1.2.30 Л е м м а (Н.С. Черников [27]). Пусть  – конечная группа, разложимая в произведения  некоторых подгрупп  и  и нильпотентной подгруппы   – подгрупа группы  содержащая  такая, что пересечения  и  нильпотентны. Тогда если подгруппы  и  инваривнтны соответственно в  и  то их нормальные замыкания в  нильпотентны.

1.2.31 Л е м м а. Произвольная группа, которая может быть получена каким-нибудь конечным множеством своих субнормальных нильпотентных подгрупп конечного индекса, нильпотентна.

1.2.32 Т е о р е м а (Ф. Холл [28]). Для произвольной конечной разрешимой группы  справедливо утверждение: при любом непустом множестве  простых чисел силовские -подгруппы группы  сопряжены в ней и являются ее холловыми -подгруппами.

1.2.33 Т е о р е м а (Ф. Холл [28,30], Чунихин [29]).

1) Конечная группа  обладающая для любого  холловой -подгруппой, разрешима.

2) Конечная группа  представимая в виде произведения некоторых своих попарно перестановочных -подгрупп по разным простым  (или, что равносильно, обладающая полной силовской базой, представимая в виде произведения некоторых своих попарно перестановочных примарных подгрупп), разрешима.

1.2.34 Т е о р е м а (Ф. Холл [28,30]). Конечная группа разрешима тогда и только тогда, когда она разложима в произведение попарно перестановочных -подгрупп по разным простым

1.2.35 Т е о р е м а (Кегель [31] – Виландт [4]). Конечная группа, представимая в виде произведения некоторых своих попарно перестановочных нильпотентных подгрупп, разрешима.

1.2.36 Т е о р е м а. Пусть  – некоторое множество простых чисел;  – группа, факторизуемая подгруппами  и  где  – -группа, а  такова, что  Тогда  является силовской -подгруппой группы

1.2.37 Л е м м а. Пусть  – группа, факторизуемая двумя подгруппами  и  где  – -, а  – -подгруппа группа  Если в  все силовские -подгруппы или все силовские -подгруппы сопряжены, то

1.2.38 Л е м м а (Гардинер, Хартли, Томкинсон [33]). Пусть  – группа,  – ее инвариантная подгруппа,  – -подгруппа группы  для некоторого непустого множества  простых чисел. Если  является силовской -подгруппой группы  и  – силовской -подгруппой группы  то  является силовской -подгруппой группы

1.2.39 Т е о р е м а (С.Н. Черников [34, 35]). Группа, факторизуемая двумя нильпотентными подгруппами, конечными над своими центрами, разрешима.

2.1.1 Л е м м а. Пусть группа  есть произведение своих подгрупп  и ,  – некоторое множество простых чисел. Тогда справедливы следующие утверждения.

1) пусть  является -группой, а  и  – -группами. Тогда найдутся холловы -подгруппы  и  подгрупп  и  соответственно такие, что  есть холлова -подгруппа ;

2) если подгруппы  и  -замкнуты, то .

2.1.2 Т е о р е м а (Васильев А.Ф. [5]). Пусть  – ненильпотентная разрешимая группа, где  и  – -разложимые подгруппы группы . Если  имеет единственную минимальную нормальную подгруппу , где  и , то справедливы следующие утверждения:

1) ;

2) ;

3) если , то  является -группой, а  – -группой.

Д о к а з а т е л ь с т в о. Установим справедливость утверждения 1). Так как  ненильпотентна,  и  – минимальная нормальная подгруппа в , то в  найдется максимальная подгруппа  такая, что . Из единственности  и  следует, что , т.е. . Кроме того, .

Ввиду 1) леммы 2.1.1 в  и  существуют холловы -подгруппы  и  соответственно и силовские -подгруппы  и  соответственно такие, что  есть холлова -подгруппа, а  есть силовская -подгруппа группы .

По условию  и . Поэтому

Откуда , так как . Но . Значит, .

Рассмотрим пересечение . Так как ,  – -группа и все дополнения к  в  сопряжены, то можно считать, что . Возьмем подгруппу Фиттинга  подгруппы . Поэтому,

. Следовательно,  – -группа. Так как , то . Поэтому . Отсюда и из  следует, что . Заметим, что  является силовской -подгруппой в . Поэтому . Ввиду минимальности  либо , либо . Случай  невозможен, так как . Поэтому , т.е. . Теперь из ,  и  получаем, что  – -группа. Из -разложимости  и  следует, что . Но тогда . Это означает, что .

Теперь из  и , ввиду  и  получаем, что . Утверждение 1) доказано.

Докажем 2). Исследуем пересечения  и . Заметим, что

и

где  и . Покажем, что . Допустим противное. Если  делит , то в  найдется -подгруппа . Так как , то

есть -разложимая группа. Аналогично,  – -разложимая группа. Отсюда и из того, что  и  есть холловы -подгруппы в  и  получаем, что . По доказанному выше подгруппа Фиттинга  из  и  являются -группами. Следовательно, . Противоречие. Тогда  есть -группа. Это невозможно, так как . Итак, .

Покажем, что . Так как , то . С другой стороны

Значит, , т.е. .

Итак, . Обозначим  и . Так как , то . Из -разложимости  и  следует, что  и . Тогда . Ввиду того, что , имеем

Значит,  и .

Покажем, что  и  являются нормальными подгруппами группы . Так как  и  – -разложимы и , то по 2) леммы 2.1.1 получаем . Так как  – -группа и , то . Значит, , т.е. . А значит, . Из  следует, что . Отсюда и из  получам, что . Аналогично . Отсюда подгруппа  нормализует , а  нормализует . Следовательно, холлова -подгруппа  группы  нормализует подгруппы  и . Так как , то  нормализует . Далее, если , то . Таким образом, и  нормализует . Следовательно, силовская -подгруппа  группы  нормализует . Тогда  нормальна в . Аналогично доказывается, что .

Из минимальности  следует, что либо , либо . Рассматривая отдельно случаи ,  и , , нетрудно видеть, что . Утверждение 2) доказано.

Установим справедливость 3). Пусть . Из -разложимости  и  следует, что . Тогда  является холловой -подгруппой группы . Из  и -разложимости  следует, что . По доказанному выше (см. доказательство утверждения 1))  – -группа. Следовательно, . Итак,  является силовской -подгруппой, а  – холловой -подгруппой группы . Лемма доказана.

Некоторые признаки приналежности насыщенной формации ди-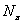-разложимых групп

2.2.1 О п р е д е л е н и е. Пусть  – непустая формация. Подгруппа  группы  называется:

1) -субнормальной в , если либо , либо существует максимальная цепь подгрупп  такая, что  для всех  (обозначается );

2) -достижимой в , если существует цепь подгрупп  такая, что либо подгруппа  субнормальна в , либо  для любого  (oбозначается ).

Нам потребуются известные свойства -достижимых и -субнормальных подгрупп, которые собраны в следующих леммах.

2.2.2 Л е м м а. Пусть  – непустая наследственная формация. Тогда справедливы следующие утверждения:

1) если  – подгруппа группы  и , то ;

2) если  ,  – подгруппа из , то  (сответственно

3) если  и  -субнормальны (-достижимы) в , то  -субнормальна (соответственно -достижима) в ;

4) если все композиционные факторы группы  принадлежат формации , то каждая субнормальная подгруппа группы  является -субнормальной;

5) если  , то  (соответственно ) для любого .

2.2.3 Л е м м а. Пусть  – непустая формация. Тогда справедливы следующие утверждения:

1) если   и , то  (соответственно

2) если   и , то  (соответственно

3) если   и  , то  (соответственно ).

2.2.4 Т е о р е м а (Васильев А.Ф. [5]). Пусть  – насыщенная наследственная формация. Тогда следующие утверждения эквивалентны.

1) если , где  и  – -достижимые нильпотентные подгруппы группы  и , то группа ;

2) если , где  и  – -субнормальные нильпотентные подгруппы группы  и , то группа ;

3) любая бипримарная минимальная не -группа является дисперсивной.

Д о к а з а т е л ь с т в о. Нетрудно видеть, что всякая -субнормальная подгруппа в  является -достижимой. Поэтому из 1) следует 2).

Докажем, что из 2) следует 3). Пусть  – бипримарная минимальная не -группа. Предлоложим, что  недисперсивна. Так как  разрешима и ненильпотентна, то . Так как  – собственная подгруппа из , то найдется  и силовская -подгруппа  из  такая, что . Но тогда , где  и  – некоторая максимальная подгруппа из . Из  следует, что , а значит, . Следовательно, . Отсюда и из 1) леммы 2.2.2 следует, что любая силовская -подгруппа из  является -субнормальной в . Если  – какая-либо силовская -подгруппа группы , , то из недисперсивности  следует, что . Из  и наследственности формации  вытекает, что . Ввиду 2) леммы 2.2.3 получаем, что . Так как  и , то . Отсюда и из наследственности формации  следует, что . Из 3) леммы 2.2.3 вытекает, что . Таким образом,  факторизуется своими -субнормальными силовскими подгруппами. Очевидно, . Поэтому по 2) теоремы 2.2.4 . Противоречие с . Следовательно,  дисперсивна.

Докажем, что из 3) следует 1). Пусть группа  – наименьший по порядку контрпример к утверждению 1) теоремы. Тогда , где  и ,  – -достижимые -подгруппы в , но сама группа  не принадлежит формации . По теореме Виландта-Кегеля  разрешима. Если  нильпотентна, то из насыщенности  и  следует, что . Противоречие с выбором группы . Следовательно,  ненильпотентна. Пусть  – минимальная нормальная подгруппа группы . Тогда ввиду 1) леммы 2.2.3 все условия утверждения 1) теоремы 2.2.4 сохраняются для факторгруппы . Поэтому в силу выбора  получаем, что . Так как  – формация, то  – единственная минимальная нормальная подгруппа группы . Из насыщенности  следует, что . Тогда , где  – -группа ( – некоторое простое число) и  для некоторой максимальной подгруппы  группы .

По 3) теореме 2.1.2, не теряя общности рассуждений, можно считать, что  – силовская -подгруппа, а  – холлова -подгруппа группы . Ясно, что . Пусть  – произвольная собственная подгруппа группы . По теореме Холла , где  – силовская -подгруппа, а  – холлова -подгруппа группы . Заметим, что , а  для некоторых элементов . Следовательно,  динильпотентна с нильпотентными факторами  и . Далее из  и  следует по 3) леммы 2.2.3, что  и . Из  и насыщенности  вытекает, что  и . Тогда по 2) леммы 2.2.2  и . Следовательно, ввиду выбора  получаем, что . Итак,  – минимальная не -группа. Покажем, что  бипримарна. Так как все дополнения к  в  сопряжены, то можно считать, что . Тогда из  и  следует, что . Значит,

. Следовательно,  является -группой. Покажем, что  – -группа, где  – некоторое простое число, отличное от . Предположим, что  и . Тогда найдутся подгруппы  и  в  такие, что  и , где  – силовская -подгруппа, а  – холлова -подгруппа из . Рассмотрим подгруппы , . Так как , то , . Так как по условию формация  насыщена, то она является локальной. Пусть  – максимальный внутренний локальный экран формации , который существует и единственен. Ввиду  и  получаем . Следовательно,  – -группа, . Из  и  получаем, что , . Значит,  – наследственная формация. Поэтому , . Заметим, что . Аналогично, . Но тогда . Из  и  следует, что . Получили противоречие с выбором .

Итак,  – примарная группа, а значит,  бипримарна. По 3) теоремы 2.2.4  дисперсивна. Следовательно,  – максимальная подгруппа группы . Так как , то . Это означает, что  – -абнормальная максимальная подгруппа группы . Ясно, что подгруппа  ненормальна в . Получили противоречие с . Итак, наше допущение неверно. Теорема доказана.

Пусть  – формация всех сверхразрешимых групп. Подгруппа  разрешимой группы  является -субнормальной в  тогда и только тогда, когда либо , либо существует максимальная цепь подгрупп  такая, что  – простое число для любого .

2.2.5 Т е о р е м а (Васильев А.Ф. [5]). Группа сверхразрешима тогда и только тогда, когда её можно представить в виде произведения двух своих нильпотентных -субнормальных подгрупп.

Д о к а з а т е л ь с т в о. Пусть  сверхразрешима. Тогда коммутант  нильпотентен. Возьмем добавление  к  в . Следовательно,

Отсюда и из

получаем, что . Итак, , где  и  – нильпотентные -субнормальные подгруппы группы .

Обратное утверждение следует из теоремы 2.2.4 ввиду того, что любая минимальная несверхразрешимая бипримарная подгруппа является дисперсивной.

2.2.6 Т е о р е м а. Пусть  – наслественная насыщенная формация, причем  и  – ди--разожимая группа. Тога справиливы следующие утверждения:

1) если   и  то

2) если   и  то

Д о к а з а т е л ь с т в о.

Докажем утверждение 1). Пусть группа  – наименьший по порядку контрпример к утверждению 1) теоремы. Тогда  – ди--нильпотентная группа, где  и  нормальна в ,  – -достижимая подгруппа в , но сама группа  не принадлежит формации . Если  нильпотентна, то из насыщенности  и  следует, что . Противоречие с выбором группы .

Пусть  ненильпотентна и  – минимальная нормальная подгруппа группы . Тогда ввиду 1) леммы 2.2.3 все условия утверждения 1) теоремы 2.2.4 сохраняются для факторгруппы . Поэтому в силу выбора  получаем, что . Тогда , где  – -группа ( – некоторое простое число) и  для некоторой максимальной подгруппы  группы .

Если  то из  и  следует, что  Противоречие с выбором  Будем считать, что  По 3) теоремы 2.1.2 можно считать, что  – силовская -подгруппа, а  – холлова -подгруппа группы  либо  – холлова -подгруппа, а  – силовская -погруппа.

Рассмотрим вначале первый случай. Тогда  и  Так как все дополнения к  в  сопряжены, то можно считать, что  Тогда из  и  следует, что . Из  и  следует, что . Следовательно, . Так как , то  – -абнормальная подгруппа в  Ясно, что  ненормальна в  Получили противоречие с -достижимостью подгруппы

Рассмотрим второй случай. Пусть  – силовская -группа, а  – холлова -группа. В этом случае  и  причем  Получили противоречие. Следовательно,  и  – нильпотентная -группа. Снова получили противоречие. Так как любая -субнормальная подгруппа является -достижимой, то утверждение 2) следует из утверждения 1). Теорема доказана.

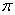-классы Шунка и их проекторы

Для доказательства основных результатов нам потребуются некоторые факты, получены в работе Васильевой Т.И. [34].

В каждой разрешимой группе -полупроекторы сопряжены и совпадают с -проекторами. Однако, в -разрешимых группах указанное утверждение не всегда имеет место. Введение -класса Шунка  (т.е. класса Шунка, для которого из условия , всегда следует ) дало возможность доказать сопряженность -полупроекторов в -разрешимых группах.

3.1.1 Л е м м а. Пусть –-класс Шунка;  – нормальная -подгруппа группы ;  – -полупроектор  Тогда  является -полупроектором группы .

Д о к а з а т е л ь с т в о. Ввиду того, что  и  имеем  Тогда по определению -класса Шунка

Предположим, что  и , где  – произвольная нормальная в  подгруппа. Тогда

Из определения -полупроектора получаем

Лемма доказана.

3.1.2 Л е м м а. Пусть –-класс Шунка;  – нильпотентная нормальная подгруппа -разрешимой группы  и  Тогда:

1) существует такая максимальная -подгруппа  группы  что

2) любые две такие максимальные -подгруппы  и  группы  что  сопряжены с помощью элемента из

Д о к а з а т е л ь с т в о. Ввиду насыщенности  можно считать, что  не содержится в . Поэтому,  где  есть добавление к  в . Следовательно, имеем . Тогда

так как , поэтому . Выбрав в  максимальную -подгруппу , содержащую , получаем 1).

Докажем 2) индукцией по . Предположим, что – группа наименьшего порядка, в в которой существуют такие максимальные -подгруппы  и , что , но  и  не сопряжены с помощью элемента из . Тогда  не принадлежит  и найдется примитивная фактор-группа , не принадлежащая , при этом  не содержится в  и .

Из примитивности  следует существование максимальной подгруппы  с ядром 1. Поскольку

 максимальна в  и , имеем . Поэтому

и

Отсюда и из максимальности  в  получаем, что  – минимальная нормальная подгруппа группы .

Если  – -группа, то лемма 3.1.1 дает противоречие . Значит,  – абелева -группа, . Тогда и  и  – максимальные подгруппы в  с единичными ядрами, . Тогда имеем

где . Так как , то найдутся такие , что .

Тогда  Откуда .

Рассмотрим . Подгруппа нильпотентна и нормальна в  и  – максимальные -подгруппы в  и . По индукции найдется такой элемент , что . Лемма доказана.

3.1.3 Л е м м а. Пусть  – -класс Шунка; – -разрешимая группа; – нильпотентная нормальная подгруппа в ;  – -полупроектор  и –такая максимальная -подгруппа группы , что . Тогда – -полупроектор группы .

3.1.4 Л е м м а. Пусть  – -класс Шунка;  – -разрешимая группа;  – такой нормальный ряд группы , что  –  – группа или нильпотентная группа, . Подгруппа  группы  является -полупроектором тогда и только тогда, когда  – максимальная -подгруппа группы .

3.1.5 Т е о р е м а. Пусть  – -класс Шунка;  – -полупроектор -разрешимой группы . Тогда  будет -полупроектором и в любой содержащей его подгруппе .

3.1.6 С л е д с т в и е. Для -класса Шунка  в любой -разрешимой группе понятия -полупроектора и -проектора совпадают.

Следующие две теоремы несут информацию о сопряженности и строении -проекторов.

3.1.7 Т е о р е м а. Пусть  – -класс Шунка;  – -разрешимая группа;  и  – -проекторы группы ;  – -группа или нильпотентная группа. Тогда  и  сопряжены с помощью элемента из

3.1.8 Т е о р е м а. Для -класса Шунка  в каждой -разрешимой группе любой -проектор содержит некоторую -холловскую подгруппу группы.

Д о к а з а т е л ь с т в о. Пусть  – -разрешимая группа наименьшего порядка, для которой теорема неверна. Тогда в ней существует -проектор , который не содержит ни одной -холловской подгруппы группы . Выберем в  минимальную нормальную подгруппу . По индукции -проектор  содержит некоторую -холловскую подгруппу  группы . Тогда -холловская подгруппа  группы  содержится в . Если  – -группа, то  и, используя лемму 1, получаем . Противоречие. Поэтому  – абелева -группа для некоторого . Тогда  для , что противоречит выбору  Теорема доказана.

Следующая теорема указывает на существование и сопряженность подгрупп, являющихся обобщением подгрупп Картера в -разрешимой группе.

3.1.9 Т е о р е м а. Любая -разрешимая группа  обладает по крайней мере одной -картеровой подгруппой и любые две из них сопряжены в

Д о к а з а т е л ь с т в о. Пусть  – класс -нильпотентных групп. Так как  является насыщенной формацией и из условия  всегда следует, что , то  есть -класс Шунка.

Пусть  – -проектор группы . Тогда  -нильпотентна и по теореме 3 содержит некоторую -холловскую подгруппу группы . Для  можно выбрать такую подгруппу , содержащую , что  – нильпотентная группа. Тогда . Так как  является -проектором , то . Но тогда . Противоречие. Следовательно, . Первая часть теоремы доказана.

Пусть теперь  – -картерова подгруппа группы . Покажем, что  есть -проектор . Пусть .

Предположим, что . Тогда в  существует такая максимальная подгруппа , что . Так как некоторая -холловская подгруппа  группы  содержится в  и  -нильпотентна, то  является нильпотентной группой. Поэтому максимальная подгруппа

Следовательно, . Для любого  подгруппа  является -картеровой подгруппой группы , а значит, и  По индукции для  теорема верна, поэтому  и  сопряжены в . Тогда по обобщенной лемме Фраттини , что противоречит тому, что  и . Значит,  т.е.  есть -проектор . Так как любые два -проектора сопряжены в  то этим доказательство теоремы завершено.

Следующая теорема указывает на существование и сопряженность подгрупп, являющихся обобщением подгрупп Гашюца в -разрешимой группе.

3.1.10 Т е о р е м а. Любая -разрешимая группа  обладает -гашюцевой подгруппой и любые две из них сопряжены в .

Д о к а з а т е л ь с т в о. Пусть  – класс -сверхразрешимых групп. Так как  является насыщенной формацией, то  – класс Шунка. Если , то и , так как  Поэтому есть -класс Шунка. м

Пусть  – -просктор группы . Тогда  -свсрхразрешима и по теореме 3 содержит некоторую -холловскую подгруппу группы . Предположим, что  и  – простое число. Возьмем в  минимальную нормальную подгруппу  Тогда

и  – самоцентрализуемая подгруппа в . Поэтому

изоморфна подгруппе циклической группы . Таким обрaзом,  сверхразрешима, т.е. принадлежит . Так как  – -проектор , то получаем . Противоречие. Следовательно, если , то  есть составное число. Первая часть теоремы доказана.

Пусть  – -гашюцева подгруппа группы . Пусть  и . Предположим, что . Тогда  содержится в некоторой максимальной подгруппе  группы . Так как  является максимальной подгруппой -сверхразрешимой группы  и  содержит -холловскую подгруппу группы , то  для некоторого , что дает противоречие . Значит  т.е.  есть -проектор группы . Так как любые два -проектора сопряжены в , то этим доказательство теоремы завершено.

Проекторы произведений ди--разложимых групп

3.2.1 Т е о р е м а. Пусть  – -класс Шунка,   – произведение -разложимых подгрупп  и  группы  причем

 Тогда в  имеется факторизуемый относительно  -проектор.

Д о к а з а т е л ь с т в о. Предположим, что теорема не верна. Пусть  – ди--разложимая группа такая, что любой -проектор группы  не факторизуется относительно

Пусть  – минимальная нормальная подгруппа группы . Тогда для фактор-группы  утверждение теоремы выполняется. Следовательно, существует  – -проектор группы  который факторизуется относительно  то есть

и

Отсюда следует, что  и  Тогда  Откуда  т.е.  факторизуется относительно

Пусть  – некоторый -проектор группы . Тогда  является -проектором группы  и  Рассмотрим два случая.

1)  Тогда  – ди--разложимая группа и для  все условия теоремы выполняются. Поэтому найдется такой , что  – факторизуемый -проектор группы , т.е.  и  Следовательно,  – факторизуемый -проектор относительно

2) Пусть  для любой минимальной нормальной подгруппы  и любого -проектора  группы . Так как , то .

Если  – не примитивная группа, то ее любая примитивная факторгруппа принадлежит . Так как  – класс Шунка, то  и  является своим -проектором. Получили противоречие с выбором .

Пусть  – примитивная группа. Тогда по теореме Бэра  имеет единственную минимальную нормальную подгруппу  такую, что  – -группа,  – некоторое простое число.  и , где  – некоторая максимальная подгруппа группы . Ясно, что  и  является -проектором группы .

Пусть . Тогда из того, что  – -класс Шунка, следует . Противоречие с выбором .

Остается принять, что  Следовательно,  является силовской -подгруппой, а  – -холловской подгруппой.

Следовательно,  поэтому найдется  такой что  факторизуется относительно

Теорема доказана.

Так как всякая насыщенная формация является классом Шунка, то справедливо следующее:

3.2.2 С л е д с т в и е. Пусть  – насыщенная формация, причем  Если  – ди--разложимая группа, причем  то в  имеется хотя бы один факторизуемый относительно  -проектор.

3.2.3 О п р е д е л е н и е. Подгруппу  группы  назовем -картеровой подгруппой, если -нильпотентна,  и  содержит некоторую -холловскую подгруппу группы .

3.2.4 С л е д с т в и е. Пусть  – ди--разложимая группа. Тогда в  имеется хотя бы одна факторизуемая относительно  -картерова подгруппа.

3.2.5 О п р е д е л е н и е. Подгруппу  группы  назовем -гашюцевой подгруппой, если  -сверхразрешима, содержит некоторую -холловскую подгруппу группы  и для  есть составное число.

3.2.6 С л е д с т в и е. Пусть  – ди--разложимая группа. Тогда в  имеется хотя бы одна факторизуемая относительно  -гашюцева подгруппа.

Трудно представить себе в настоящее время теорию групп без вопросов, относящихся к группам, разложимым в произведение своих подгрупп.

Вот уже на протяжении свыше 70-ти лет исследования в абстрактной теории бесконечных групп продолжают интенсивно развиваться, причем темп и глубина исследований возрастают по мере удаления от момента получения основопологающих результатов. Самое удивительное в развитии этой теории то, что ни одно из основных ее направлений, возникших в 30–40-х годах XX в., не утратило значения до настоящего времени. Более того, на их основе возникают новые перспективные ответвления в теории групп, со временем превращающиеся в самостоятельные направления.

Получено немало важных результатов. Они отражены в ряде обзоров (см., например, Чунихин [6, 7], Азлецкий [8, 9], Кострикин [10], Чунихин, Шеметков [11], Мазуров [12], Казарин [13]).

В настоящей работе были исследованы свойства конечных разрешимых групп, представимых в произведение своих двух -разложимых подгрупп.

В классе всех конечных разрешимых групп, когда  где  – класс Шунка, и если  – ди--разложимая группа, причем , то был получен следующий результат: в  имеется хотя бы один факторизуемый относительно  -проектор.

Результаты настоящего диплома являются новыми и могут быть использованы в учебном процессе при чтении спецкурсов на математических специальностях в высших учебных заведениях.

Литература

[1] Frobenius G., Stickelberger L. Uber Gruppen von vertauschbaren Elementen // J. Reine Angew. Math. – 1879. – 86, N4, S.217–262.

[2] Huppert B. Uber das Produkt von paarweise vertauschbaren zyklischen Gruppen. // Math. Z. – 1953. – 58, N3. – S. 243–264.

[3] Amberg B., Hofling B. // Arch. Math. – 1994. – V.63. – P. 1–8.

[4] Wielandt H. Uber Produkte von nilpotenten Gruppen. // III.J. Math. – 1958. – 2, N4B. – S.611–618.

[5] Васильев А.Ф. Новые свойсва конечных динильпотентных групп // Вести НАН Беларуси. – 2004. – N 2. – C.29–33.

[6] Чунихин С.А. О некоторых направлениях в развитии теории конечных групп за последние годы. // Успехи мат. наук. – 1961. – 16, N4. – С. 31–50.

[7] Чунихин С.А. Подгруппы конечных групп. – Мн: Наука и техника, 1964. – 158с.

[8] Азлецкий С.П. О факторизации конечных групп. // Мат.зап. Урал.ун-та. – 1962. – 3, N3. – С. 3–17.

[9] Азлецкий С.П. О факторизации конечных групп. // Мат.зап. Урал.ун-та. – 1966. – 5, N3. – С. 3–14.

[10] Кострикрн А.И. Конечные группы. В кн.: Алгебра – 1964 (Итоги науки). – М: ВИНИТИ АН СССР. – 1966. – С.7–46.

[11] Чунихин С.А., Шеметков Л.А. Конечные группы. В кн.: Алгебра, Топология. Геометрия 1969 (Итоги науки). – М: ВИНИТИ АН СССР. – 1964. – 154, N3. – С.7–70.

[12] Мазуров В.Д. Конечные группы. В кн.: Алгебра. Топология. Геометрия 1976 (Итоги науки и техники). – М: ВИНИТИ АН СССР. – 1977. – С.5–56.

[13] Казарин Л.С. Группы с факторизацией. – Ярославль, 1981.–79с.–Рукопись деп. в ВИНИТИ, № 3900–81 Деп.

[14] Монахов В.С. Введение в теорию конечных групп и их классов. – Гомель, 2003.

[15] Шеметков Л.А. Формации конечных групп. – М: Наука, 1978. – С.165–204.

[16] Ballester-Bolinches A., Perez-Ramos M.D. // J. Algebra. – 1996. – V. 179. – P. 905–917.

[17] Черников С.Н. О дополняемости силовских П-подгрупп в некоторых классах конечных групп // Мат.сб. – 1955. – 37, N3. – С.557–566.

[18] Сесесекин Н.Ф. О произведении финитно связанных абелевых групп // Сиб.мат. журн. – 1968. – 9, N6. – С.1427–1430.

[19] Kegel O.H. On the solvability of some factorized linear groups // III.J. Math. – 1965. – 9, N3. – P. 535–547.

[20] Amberg B. Artinian and Noetherian factorized groups // Rend. Semin Math. Univ. Padova/ – 1976 – 55/ – P. 105–122.

[21] Amberg B. Soluble products of two locally finite groups with min- for every prime  // Rend. Semin. Mat. Univ. Padova. – 1983. – 69. – P.7–17.

[22] Чунихин С.А. О существовании подгрупп у конечной группы. В кн.: Труды семинара по теории групп. – М.; Л.:ГОНТИ. – 1938. – С. 106–125.

[23] Wielandt H. Uber das Produkt von paarweise vertauschbaren nilpotenten Gruppen // Math.Z. – 1951. – 55, N1. – S.1–7.

[24] Huppert B. Endliche Gruppen.I. – Berlin etc.: Springer, 1967. – 795s.

[25] Черников Н.С. О факторизациях локально конечных групп // Сиб. мат. журн. – 1980. – 21, N6. – С.186–195.

[26] Зайцев Д.И. Факторизации полициклических групп // Мат. заметки. – 1981. – 29, N4. – С.481–490.

[27] Черников Н.С. Произведения групп конечного свободного ранга. В кн.:Группы и системы их подгрупп. Киев: Ин-т математики АН УССР. – 1983. – С.42–56.

[28] Hall Ph. On the Sylow system of a soluble groups // Proc. London. Math. Soc. – 1937. – 43, N5. – Р.316–323.

[29] Чунихин С.А. О разешимых группах // Изв. НИИ математики и механики Том. ун-та. – 1938. – 2. – С.220–223.

[30] Hall Ph. A characteristic property of soluble groups // Ibid. – 1937. – 12, N 47. – Р.198–220.

[31] Kegel O.H. On the solvability of some factorized linear groups // III. J. Math. – 1965. – 9, N3. – Р.535–547.

[32] Черников Н.С. Группы, разложимые в произведение перестановочных подгрупп. – Киев: Навукова думка, 1987. – С.17–59.

[33] Gardiner A.D., Hartley B., Tomkinson M.J. Saturated formations and Sylow structure in locally finite groups // J. Algebra. – 1971. – 17, N2. – Р.177–211.

[34] Васильева Т.И. (Островская Т.И.) – В кн.: Вопросы алгебры. Мн: изд-во «Университетское». – 1985. – 1. – С.57–62. Докл. АН СССР. – 1980. – 255, N3. – С.537–539.

[35] Черников Н.С. О произведении почти абелевых групп // Укр. мат. журн. – 1981. – 33, N1. – С.136–138.