Реферат: Перевірка статистичних гіпотез відносно невідомих значень параметрів визначеного розподілу

Перевірка статистичних гіпотез відносно невідомих значень параметрів визначеного розподілу

1 Порівняння двох дисперсій нормальних генеральних сукупностей

Ця задача виникає в метрології при порівнянні точності приладів. Крім того, умова рівності дисперсій чи їхньої незмінності в процесі дослідження лежить в основі багатьох задач перевірки гіпотез про порівняння інших параметрів (математичного сподівання, коефіцієнтів кореляції та ін.).

Нехай генеральні сукупності  і  розподілені нормально. По незалежних вибірках, узятих з цих сукупностей, з обсягами, які дорівнюють відповідно  і , знайдено виправлені вибіркові дисперсії  і . Необхідно за цими характеристиками при заданому рівні значущості  перевірити нульову гіпотезу про те, що генеральні дисперсії даних сукупностей дорівнюють одна одній:

 : .

Оскільки виправлені дисперсії є незміщеними оцінками генеральних дисперсій, тобто , , нульову гіпотезу можна переписати також у такому вигляді:

 : .

У якості критерію перевірки нульової гіпотези про рівність генеральних дисперсій візьмемо відношення виправлених дисперсій, тобто таку випадкову величину:

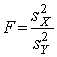. (1)

Можна впевнитися, що величина F за умови справедливості нульової гіпотези має розподіл Снедекора – Фішера (9) з  і  ступенями волі.

Таким чином, маємо нульову гіпотезу :  і конкуруючу гіпотезу : . У цьому випадку критична область при заданому рівні значимості  є двосторонньою, обумовленою сукупністю співвідношень:

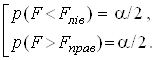 (2)

Однак, можна показати, що якщо чисельник відносини (1), що визначає випадкову величину , більше знаменника, тобто якщо > і , то першу нерівність з  перевіряти не потрібно, тому що вона виконується автоматично при невеликих рівнях значимості , що звичайно застосовують. При цьому перевірка гіпотези  зводиться до перевірки тільки другої нерівності з . Це проводиться наступним чином: по таблиці критичних точок розподілу Снедекора – Фишера з  і  ступенями волі при вибраному рівні значимості  відповідно (2) знаходять значення величини . Далі, якщо 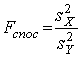<, немає причин відкинути нульову гіпотезу, якщо 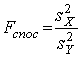> – нульову гіпотезу відкидають.

2 Порівняння виправленої вибіркової дисперсії з гіпотетичною генеральною дисперсією нормальної сукупності

Ця задача виникає в метрології під час перевірки точності роботи приладів, інструментів щодо припустимих характеристик розсіювання.

Нехай генеральна сукупність розподілена нормально, причому генеральна дисперсія  встановлена теоретично або на основі попередніх досліджень. Потрібно перевірити її значення на основі виправленої дисперсії  з  ступенями волі, яку отримано за вибіркою обсягу .

З огляду на те, що  є незміщеною оцінкою генеральної дисперсії, нульову гіпотезу можна переписати ще так:

: .

У якості критерію перевірки нульової гіпотези тепер доцільно взяти випадкову величину , що, як можна показати, має розподіл , тому і має таке позначення. При конкуруючій гіпотезі :  критична область при заданому рівні значимості , як і в попередньому випадку, є двосторонньою і визначається сукупністю співвідношень:

дісперсія генеральний сукупність

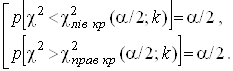 (3)

У таблиці критичних точок розподілу , також як і для -розподілу раніше, зазначено лише праві критичні точки. Але на відміну від попередньої задачі тут необхідно врахувати обидві умови (3). Для цього ми застосуємо більш універсальний прийом, придатний в обох випадках. Він заснований на очевидній рівності:

.

Використовуючи її, ліву критичну точку можна шукати, так само, як і праву.

Для перевірки нульової гіпотези необхідно обчислити значення критерію, , що спостерігається, і знайти ліву та праву критичні точки , , 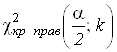відповідно.

Якщо при цьому,  – немає причин відкинути нульову гіпотезу, її приймають. Якщо  чи  – нульову гіпотезу відкидають.

3 Порівняння двох середніх нормальних генеральних сукупностей, дисперсії яких відомі (незалежні вибірки)

Нехай генеральні сукупності  і  розподілені нормально, причому їхні дисперсії відомі (з попереднього досвіду чи теоретично). По незалежних вибірках, обсяги яких дорівнюють відповідно  і , взятих з цих сукупностей, знайдено вибіркові середні  і .

Потрібно з вибіркових середніх при заданому рівні значущості  перевірити нульову гіпотезу про те, що генеральні середні (математичні сподівання) розглянутих сукупностей рівні між собою, тобто:

 : .

Конкуруючою гіпотезою є : .

З огляду на те, що вибіркові середні є незміщеними оцінками генеральних середніх, тобто  і , нульову гіпотезу можна записати ще інакше:

 : .

У якості критерію перевірки нульової гіпотези візьмемо випадкову величину

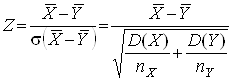, (4)

яка є нормованою нормальною розподіленою випадковою величиною [2].

Двосторонню критичну область будуємо, виходячи з вимоги, щоб імовірність влучення критерію в цю область у припущенні справедливості нульової гіпотези дорівнювала б прийнятому рівню значущості .

Можна показати, що найбільша потужність критерію досягається при рівності ймовірностей улучення критерію в кожний із двох інтервалів критичної області, тобто при

 , .

Із симетрії нормованої нормальної величини випливає симетрія і критичних точок, тобто . Тому для визначення двосторонньої критичної області досить знайти праву границю  її області, використовуючи функцію Лапласа і таблицю її значень за формулою:

чи

.

Далі треба обчислити значення критерію, що спостерігається

.

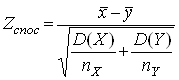Якщо виявиться, що , то причин відкинути нульову гіпотезу немає і її приймають, у противному випадку () – нульову гіпотезу відкидають.

4 Порівняння двох середніх довільно розподілених генеральних сукупностей (великі незалежні вибірки)

У попередній задачі передбачалося, що генеральні сукупності  і  розподілені нормально, а їхні дисперсії відомі. Тільки при всіх цих припущеннях у випадку справедливості нульової гіпотези про рівність середніх у незалежних вибірках критерій  (4) є нормальною нормованою величиною. Під час невиконання хоча б однієї з цих умов метод порівняння середніх, що розроблено під час розв’язання попередньої задачі, є неприйнятним.

Однак, якщо незалежні вибірки мають великий обсяг ( 30), можна показати, що вибіркові середні розподілені приблизно нормально, а вибіркові дисперсії  і  є досить гарними оцінками генеральних дисперсій, тому їх можна вважати приблизно відомими. Відповідно, критерій

,

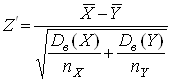що є аналогом критерію (4), має приблизно нормальний розподіл з параметрами  (за умови справедливості нульової гіпотези) і  (якщо вибірки незалежні). Тому в цьому випадку можна застосувати метод, розвинутий під час вирішення попередньої задачі, замінивши точний критерій  наближеним критерієм .

5 Порівняння двох середніх нормальних генеральних сукупностей, дисперсії яких невідомі й однакові (малі незалежні вибірки)

Нехай генеральні сукупності  і  розподілені нормально, причому їхні дисперсії невідомі. Наприклад, по вибірках малого обсягу не можна одержати гарні оцінки генеральних дисперсій. Тому не можна застосувати метод порівняння середніх, викладений раніше.

Однак якщо додатково припустити, що невідомі генеральні дисперсії є рівними між собою, то можна побудувати критерій (Стьюдента) порівняння середніх. Наприклад, якщо порівнюються середні розміри двох партій деталей, виготовлених на тому ж самому верстаті, то логічно допустити, що дисперсії розмірів, які контролюються, є однаковими.

Якщо ж немає причин вважати, що дисперсії однакові, то, перш ніж порівнювати середні, необхідно за допомогою критерія Снедекора-Фішера (1) попередньо перевірити гіпотезу про рівність генеральних дисперсій.

Далі в припущенні, що генеральні дисперсії однакові, перевіримо нульову гіпотезу : . Тобто встановимо, значимо чи незначимо розрізняються вибіркові середні  і , що знайдені по незалежних малих вибірках з обсягами  і .

Для перевірки нульової гіпотези у якості критерію застосуємо випадкову величину

 ,

що, як доведено [5], при справедливості нульової гіпотези має -розподіл Стьюдента з  ступенями волі.

Під час перевірки нульової гіпотези з конкуруючою гіпотезою :  критична область має двосторонній характер. Її будують, виходячи з вимоги, щоб ймовірність влучення критерію Т в цю область у припущенні справедливості нульової гіпотези дорівнювала б прийнятому рівню значущості .

Можна показати, що найбільша потужність критерію досягається при рівності ймовірностей влучення критерію в кожний із двох інтервалів критичної області, тобто при

 , .

Із симетрії -розподілу Стьюдента випливає симетрія і критичних точок, тобто . Тому для визначення двосторонньої критичної області досить знайти праву границю  її області в таблиці критичних точок розподілу Стьюдента при заданому рівні значущості. Зі знайденим таким способом значенням  зіставимо значення критерію, що спостерігається:

.

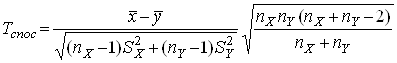Якщо , немає причин відкинути нульову гіпотезу, її приймають, у разі  – нульову гіпотезу відкидають.

6 Порівняння вибіркової середньої з гіпотетичною генеральною середньою нормальної сукупності (при відомій генеральній дисперсії)

Нехай генеральна сукупність  розподілена нормально з дисперсією , причому невідома генеральна середня  приблизно дорівнює значенню .

Потрібно по вибірковій середній , що отримано з вибірки обсягом , при заданому рівні значущості  перевірити нульову гіпотезу :  про рівність генеральної середньої  гіпотетичному значенню . Конкуруючу гіпотезу візьмемо у вигляді: .

З огляду на те, що вибіркова середня є незміщеною оцінкою генеральної середньої, тобто , нульову гіпотезу можна переписати у вигляді: .

У якості критерію перевірки нульової гіпотези візьмемо таку випадкову величину

,

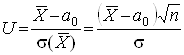яку можна показати, при справедливості нульової гіпотези, є нормованою нормальною величиною.

Далі обчислюємо значення критерію, що спостерігається:

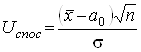 (5)

і по таблиці Лапласа знаходимо критичну точку двосторонньої критичної області зі співвідношення

.

Якщо  – немає причин, щоб відкинути нульову гіпотезу; при  – нульову гіпотезу відкидають.

7 Порівняння вибіркової середньої з гіпотетичною генеральною середньою нормальної сукупності (при невідомій генеральній дисперсії)

У випадку невідомої генеральної дисперсії у якості критерію перевірки нульової гіпотези :  при конкуруючій гіпотезі  приймають випадкову величину

,

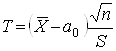де  – "виправлене" середнє квадратичне відхилення. Можна показати, що величина  підкоряється -розподілу Стьюдента з  ступенями волі.

Критична область будується так само, як описано вище. Далі обчислюється значення критерію, що спостерігається:

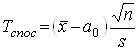 (6)

та по таблиці критичних точок розподілу Стьюдента при заданому рівні значущості  і числі ступенів волі  знаходиться критична точка  у відповідності до умови .

Якщо  – немає причин відкинути нульову гіпотезу і її приймають; при  нульову гіпотезу відкидають.

8 Зв'язок між двосторонньою критичною областю і довірчим інтервалом

Очевидно, що під час побудови двосторонньої критичної області при заданому рівні значущості  попутно визначається і відповідний довірчий інтервал для значень, що приймаються випадковою величиною з надійністю . Перевірка нульової гіпотези :  при :  проводилася на основі умови, що ймовірність влучення критерію 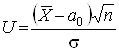 в двосторонню критичну область дорівнювала б рівню значущості , отже, ймовірність влучення критерію в область прийняття гіпотези  дорівнює . Тобто з надійністю  виконується нерівність

,

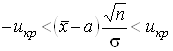або рівносильна їй нерівність

, (7)

де  визначається з рівності .

Подвійна нерівність (7) є довірчим інтервалом для оцінки математичного сподівання  нормального розподілу при відомому  із надійністю .

9 Визначення мінімального обсягу вибірки при порівнянні вибіркової і гіпотетичної генеральної середніх

Дуже важливою практичною задачею є визначення мінімального обсягу вибірки, що є необхідним для одержання на її основі обґрунтованих висновків щодо генеральної середньої з наперед заданою точністю  (її смисл – гранична величина різниці між вибірковою і гіпотетичною генеральною середніми).

Наприклад, звичайно потрібно, щоб середній розмір виготовлених деталей відрізнявся від номінального розміру не більше ніж на задану величину . Для проведення контролю з партії виготовлених деталей (генеральна сукупність) відбирається вибірка. Треба з'ясувати, яким має бути мінімальний обсяг цієї вибірки, в якій відсутні браковані деталі, щоб з ймовірністю , де  – рівень значущості, гарантувати, що і в усій партії їх зовсім немає?

Як показано в попередньому пункті, задача визначення довірчого інтервалу для оцінки математичного сподівання нормального розподілу при відомому  і задача відшукання двосторонньої критичної області для перевірки гіпотези про рівність вибіркової середньої гіпотетичній генеральній середній нормальної сукупності зводяться одна до одної. Тому з формули (5) при заміні  на  та  на  випливає, що мінімальний обсяг вибірки має дорівнювати:

 ,

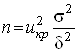де  знаходиться з рівності .

При невідомому  аналогічно скористаємося формулою (6), замінюючи  на . Тоді:

.
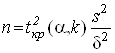