Курсовая работа: Железобетонные конструкции
Характеристики прочности бетона и арматуры
Бетон В45:
Нормативная прочность бетона на сжатие для предельных состояний соответственно первой группы – Rbn=32МПа,
Расчетная прочность бетона на сжатие для предельных состояний второй группы – Rb, ser=32МПа;
Нормативная прочность бетона на растяжение для предельных сотояний первой группы – Rbtn=2,2 МПа;
Расчетная прочность бетона на растяжение для предельных состояний второй группыRbt, ser=2,2МПа;
Расчетная прочность бетона на сжатие для предельных состояний первой группы – Rb=25МПа;
Расчетная прочность бетона на растяжение на растяжение для предельных состояний первой группы – Rbt=1,45МПа;
Начальный модуль упругости бетона при сжатии – Eb=34*103 МПа;
Арматура А 1000:
Нормативная прочность арматуры на растяжение для первой группы предельных состояний – Rsn=980МПа;
Расчетная прочность арматуры на растяжение для второй группы предельных состояний – Rs, ser=980МПа;
Расчетная прочность арматуры на растяжение для первой группы предельных состояний – Rs=815МПа;
Расчетная прочность арматуры на сжатие для первой группы предельных состояний – Rsc=390МПа;
Модуль упругости продольной арматуры – Es=19*104 МПа;
Предварительное напряжение арматуры:
![]() ; (1)
; (1)
![]()
Проверяю условия:
![]()
![]() sp=0.05
sp=0.05![]() sp, (2)
sp, (2)
![]()
![]() sp=0.05*735=36,75
sp=0.05*735=36,75
![]() ; (3)
; (3)
![]()
771,75<980 – Условие выполняется;
Предельное отклонение предварительного напряжения:
 , (4)
, (4)
где n – число арматурных стержней=2;

![]() ; (5)
; (5)
![]()
При проверке по образование трещин в верхней зоне плиты при обжатии принимаем
![]()
![]()
Предварительное напряжение с учетом натяжений
![]()
![]() – с учетом потерь.
– с учетом потерь.
Расчет пустотной плиты в предельном состоянии первой группы
Расчетный пролет и нагрузки
Для установления расчетного пролета плиты предварительно задаюсь размерами сечения ригеля:
Высота –  , (6)
, (6)
где l – длина ригеля;
![]()
Ширина – ![]() , (7)
, (7)
![]()
50х20 см-размеры ригеля
При опирании на ригель поверху расчетный пролет:
![]() , (8)
, (8)
![]()
Таблица 1 – Нормативные и расчетные нагрузки на 1м2 перекрытия
| Нагрузка |
Нормативная нагрузка, Н/ м2 |
Коэффициент надежности по нагрузке |
Расчетная нагрузка, Н/ м2 |
|
Постоянная: многопустотная плита с круглыми пустотами слой цементного раствора, δ=20 мм (ρ=2200 кг/м3 ) керамические плитки, δ=13 мм (ρ=1800 кг/м3) |
3000 440 240 |
1,1 1,3 1,1 |
3300 570 264 |
| Итого | 3680 | - | 4134 |
|
Временная В том числе: длительная кратковременная |
5000 2000 3000 |
1,2 1,2 1,2 |
6000 2400 3600 |
|
Полная нагрузка В том числе: постоянная и длительная кратковременная |
8680 7180 1500 |
- - - |
10134 - - |
Расчетная нагрузка на 1 м2 при ширине плиты 1,533 м.
постоянная
![]()
полная
![]()
![]()
Нормативная нагрузка на 1 м:
постоянная
![]()
полная
![]()
в том числе постоянная и длительная
![]()
Усилия от расчетных и нормативных нагрузок
От расчетной нагрузки
![]() ; (9)
; (9)
 .
.
![]() ; (10)
; (10)
![]()
От нормативной полной нагрузки

От нормативной постоянной и длительной нагрузок
![]()
Установление размеров сечения плиты
Высота сечения многопустотной (7 круглых пустот диаметром 15,9 см) предварительно напряженной плиты:
![]()
Рабочая высота сечения:
![]() ; (12)
; (12)
![]()
Толщина верхней и нижней полок (22–15,9) 0,5=3,05 см.
Ширина ребер: средних-3,5 см; крайних-4,65 см.
В расчетах по предельным состояниям первой группы расчетная толщина сжатой полки таврового сечения h'ƒ=3 см; отношение h'ƒ/h=3/22=0,14›0,1, при этом в расчет ввожу всю ширину полки b'ƒ=1500 мм;
расчетная ширина ребра
![]()
Расчет прочности плиты по сечению, нормальному к продольной оси
М=72 кНм. Сечение тавровое с полкой в сжатой зоне.
 ; (13)
; (13)
 .
.
Нахожу из таблицы III.1 учебника В.Н. Байкова коэффициент ξ=0,07;
![]() ; (14)
; (14)
![]()
1,33 см ‹ 3 см – нейтральная ось проходит в пределах сжатой полки; η=0,965.
Характеристика сжатой зоны:
![]() ; (15)
; (15)
![]()
Граничная высота сжатой зоны:
 , (16)
, (16)
где в знаменателе формулы ξR принимаю 500 МПа, поскольку γb2‹1;
![]() ; (17)
; (17)
![]()

Коэффициент условий работы, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести, согласно формуле:
 ; (18)
; (18)
![]()
здесь η=1,15 – для арматуры класса А-1000;
принимаем γs6=η=1,15.
Вычисляю площадь сечения растянутой арматуры:
 ; (19)
; (19)

Принимаю 6Ø10 А-1000, As=4,71см2.
Расчет прочности плиты по сечению, наклонному к продольной оси
Проверяю, требуется ли поперечная арматура по расчету по первому условию:
![]() ; (20)
; (20)

Проверяю, требуется ли поперечная арматура по расчету по второму условию:
![]() (21)
(21)
Для того, чтобы подсчитать Q вычисляем q1:
![]() ; (22)
; (22)
![]()
Сравниваем ![]() , (23)
, (23)
![]()
![]()
Условие выполняется, назначаю С=Сmax=2,5ho;
C=2,5·190=475 мм.
Для определения Q вычисляю:
![]() ; (24)
; (24)
![]()

![]()
Проверяю прочность бетона по сжатой полосе по условию:
![]() (25)
(25)
где ![]()
![]()
![]()
![]()
![]()
Условие выполняется
Расчет многопустотной плиты по предельным состояниям второй группы
Геометрические характеристики приведенного сечения
Круглое очертание пустот заменяю эквивалентным квадратным со стороной h=0,9в=0,9*1,59=14,3 см. Толщина полок эквивалентного сечения h'f=3 см. Ширина ребра 150–7*14,3=49,9. Ширина пустот 150–49,9=100,1 см. Площадь приведенного сечения Ared=150*22–100,1*14,3=1869 см2 (пренебрегаю ввиду малости величиной νАs).
Расстояние от нижней грани до центра тяжести приведенного сечения:
![]() (26)
(26)
![]()
Момент инерции сечения (симметричного):

Момент сопротивления сечения по нижней зоне:
 ; (27)
; (27)
![]()
![]()
Расстояние от ядровой точки, наиболее удаленной от растянутой зоны (верхней), до центра тяжести сечения по формуле:
 ; (28)
; (28)
![]()
то же, наименее удаленной от растянутой зоны (нижней) rinf =4,49 см, здесь:
 ; (29)
; (29)
![]()
Отношение напряжения в бетоне от нормативных нагрузок и усилия обжатия к расчетному сопротивлению бетона для предельных состояний второй группы предварительно принимаю равным 0,75.
Упругопластический момент сопротивление по растянутой зоне, согласно формуле:
![]() ; (30)
; (30)
![]()
Потери предварительного напряжения арматуры
Коэффициент точности натяжения арматуры принимаю γsp=1.
σ1 – потери от релаксации напряжений в арматуре при электротермическом способе натяжения:
![]() ; (31)
; (31)
![]()
σ2 – температурный перепад (разность температур натянутой арматуры в зоне нагрева и устройства, воспринимающего усилие натяжения при прогреве бетона). В процессе термообработки при подтяжке напрягаемой арматуры, компенсирующей потери от температурного перепада. Принимаю равным 0.
σ3 – деформации анкеров, расположенных у натяжных устройств. При электротермическом способе натяжения, потери от деформаций анкеров в расчете не учитываю, так как они учтены при определении полного удлинения арматуры. Принимаю равным 0.
σ4 – трение арматуры об огибающие приспособления. Так как огибающих приспособлений в конструкции нет, принимаю равным 0.
σ5 – деформации стальной формы при неодновременном натяжении арматуры на форму. При электротермическом способе натяжения потери от деформаций форм в расчете не учитываю, так как они учтены при определении полного удлинения арматуры.
σ6 – быстронатекающая ползучесть. Рассчитываю по формуле:
![]() , (32)
, (32)
при σbp/Rbp≤α,
где α=0,25+0,025*Rbp=0,25+0,025*22.5=0.813,
σbp – напряжение в бетоне в стадии предварительного обжатия, определяемые на уровне центров тяжести сечения продольной арматуры s и s' с учетом потерь от α1 до α5.
Для бетона, подверженного тепловой обработке, значение потерь умножаю на 0,85:
 ; (33)
; (33)
Усилие
обжатия – ![]() ; (34) Эксцентриситет этого усилия
относительно центра тяжести сечения
; (34) Эксцентриситет этого усилия
относительно центра тяжести сечения
![]() ; (35)
; (35)
![]() ;
;
![]()
![]()
![]()
Устанавливаю величину передаточной прочности бетона из условия:


Принимаем Rbp=22,5 МПа
Тогда отношение σbp/Rbp=4,03/22,5=0,18.
Вычисляю сжимающие напряжения в бетоне на уровне центра тяжести площади напрягаемой арматуры от усилия обжатия (без учета момента от веса плиты):

Потери от быстронатекающей ползучести при σbp/Rbp=3,4/22,5=0,15‹0,5;
![]()
Первые потери:
![]() ; (36)
; (36)
![]()
σbp/Rbp=0,18
σ8 – усадка бетона класса В45 и ниже. Принимаю равной 60. Для бетона, подверженного тепловой обработке при атмосферном давлении, значение потерь умножаю на 0,85. σ8=0,85*60=51МПа.
σ9 – ползучесть бетона по формуле:
![]()
 ; (37)
; (37)
![]()
При σbp/Rbp≤0,75. Для бетона, подверженного тепловой обработке при атмосферном давлении, значение потерь умножаю на 0,85.
Вторые потери:
![]() ; (38)
; (38)
![]()
Полные потери:
![]() ; (39)
; (39)
![]()
Усилие обжатия с учетом полных потерь:
![]() ; (40)
; (40)
![]()
Расчет по образованию трещин, нормальных к продольной оси
Производится для выяснения необходимости проверки по раскрытию трещин. При этом для элементов, к трещиностойкости которых предъявляются требования третьей категории, принимаю значение коэффициентов надежности по нагрузке γf=1; М=61,5кНм. М≤Мcrc. Вычисляю момент образования трещин по приближенному способу ядровых моментов по формуле:
![]() ; (41)
; (41)
где ![]() ; (42)
; (42)
![]()
![]()
Поскольку М=61,5›Мcrc=50кНм, трещины в растянутой зоне образуются. Следовательно, необходим расчет по раскрытию трещин.
Проверяю, образуются ли начальные трещины в верхней зоне плиты при ее обжатии при значении коэффициента точности натяжения γsp=1,14 (момент от веса плиты не учитываю). Расчетное условие:
![]()
![]()
![]()
Условие удовлетворяется, начальные трещины не образуются.
Расчет по раскрытию трещин, нормальных к продольной оси
Предельная ширина раскрытия трещин: непродолжительная acrc =0,4 мм, продолжительная acrc =0,3 мм. Изгибающие моменты от нормативных нагрузок: постоянной и длительной М=50,8кНм; полной М=61,5кНм. Приращение напряжений в растянутой арматуре от действия постоянной и длительной нагрузок расчитываю по формуле:
![]() , (43)
, (43)
где z1 – плечо внутренней пары сил:
![]() ; (44)
; (44)
Ws – момент сопротивления сечения по растянутой арматуре:
![]() ; (45)
; (45)
![]() .
.
Т.к. усилие обжатия Р приложено в центре тяжести площади нижней напрягаемой арматуры, esn=0.
![]() ;
;
![]()
Приращение напряжений в арматуре от действия полной нагрузки:

Вычисляю по формуле:
ширина раскрытия трещин от непродолжительного действия полной нагрузки:
![]() , (46)
, (46)
где ![]() ; (47)
; (47)
![]() ;
;
![]() .
.
ширина раскрытия трещин от непродолжительного действия постоянной и длительной нагрузок:
![]()
ширина раскрытия трещин от постоянной и длительной нагрузок:
![]()
Непродолжительная ширина раскрытия трещин:
![]() ; (48)
; (48)
![]()
Продолжительная ширина раскрытия трещин:
![]()
Расчет прогиба плиты
Прогиб определяю от постоянной и длительной нагрузок, предельный прогиб f=3 см. вычисляю параметры, необходимые для определения прогиба плиты с учетом трещин в растянутой зоне. Заменяющий момент равен изгибающему моменту от постоянной и длительной нагрузок М=50,8кНм; суммарная предельная сила равна усилию предварительного обжатия с учетом всех потерь и при γsp=1, Ntot=P2=266кН; эксцентриситет es, tot=M/Ntot=5080000/266000=19 см; коэффициент φl =0,8 – при длительном действии нагрузок; по формуле:
 ; (49)
; (49)
![]()
принимаю φm=1;
коэффициент, характеризующий неравномерность деформации растянутой арматуры на участке между трещинами, по формуле:
![]() ; (50)
; (50)
![]()
Вычисляюкривизну оси при изгибе по формуле:
![]() ; (51)
; (51)
![]()
ψb=0,9; λb=0,15 – при длительном действии нагрузок; Ab=216*3=648см2.
Вычисляю прогиб по формуле:
![]() ; (52)
; (52)

Определение усилий в ригеле поперечной рамы
Расчетная схема рамы и нагрузки
Поперечная многоэтажная рама имеет регулярную расчетную схему с равными пролетами ригелей и равными длинами стоек (высотами этажей). Сечения ригелей и стоек по этажам также приняты постоянными. Такая многоэтажная рама расчленяется для расчета на вертикальную нагрузку на одноэтажные рамы с нулевыми точками моментов – шарнирами, расположенными по концам стоек, – в середине длины стоек всех этажей, кроме первого.
Нагрузка на ригель от многопустотных плит считается равномерно распределенной, от ребристых плит при числе ребер в пролете ригеля более четырех – также равномерно распределенной. Ширина грузовой полосы на ригель равна шагу поперечных рам, в примере – 6 м. Подсчет нагрузок на 1 м2 перекрытия приведен в таблице 1.3.1.
Вычисляю постоянную нагрузку на 1 м длины ригеля.
Постоянная: от перекрытия с учетом коэффициента надежности по назначению здания γn=0,95:
![]()
От веса ригеля сечением 0,25х0,55 (ρ=2500 кг/см3) с учетом коэффициентов надежности γf=1,1 и γn=0,95:
![]()
Итого:
![]()
Временная с учетом γn=0,95:
![]()
в том числе длительная:
![]()
и кратковременная:
![]()
Полная нагрузка:
![]()
Вычисление изгибающих моментов в расчетных сечениях ригеля
Опорные моменты вычисляю для ригелей, соединенных с колоннами на средних и крайних опорах жестко, по формуле:
![]()
![]()
Таблица 1.5.1 – Опорные моменты ригеля при различных схемах загружения
| Схема загружения | Опорные моменты, кНм | |||
|
М12 |
М21 |
М23 |
М32 |
|
|
-0,035*27,4* *6,6*6,6=-42 |
-0,098*27,4* *6,6*6,6=-117 |
-0,09*27,4* 6,6*6,6=-107 |
-107 | |
|
-0,044*33,4* *6,6*6,6=-64 |
-0,063*33,4* *6,6*6,6=-92 |
-0,062*33,4* *6,6*6,6=-39 |
-39 | |
|
0,009*33,4* *6,6*6,6=2 |
-0,035*33,4* *6,6*6,6=-51 |
-0,062*33,4* *6,6*6,6=-90 |
-90 | |
|
-0,034*33,4* *6,6*6,6=-49 |
-0,114*33,4* *6,6*6,6=-166 |
-0,103*33,4* *6,6*6,6=-150 |
-0,047*33,4* *6,6*6,6=-68 |
|
| 1+2 | -106 | -209 | -146 | -146 |
| 1+3 | -40 | -168 | -197 | 197 |
| 1+4 | -91 | -283 | -257 | -175 |
Таблица 1.5.2 – Ординаты моментов для свободнолежащей балки
| Схема загружения | х |
х при l=6,6 м |
l-x |
l-x при l=6,6 м |
Мх=qx (l-x)/2, кНм |
Mx=(q+v)*x*(l-x)/2, кНм |
|
0 0,2l 0,4l 0,5l 0,6l 0,8l l |
0 1,32 2,64 3,3 3,96 5,28 6,6 |
l 0,8l 0,6l 0,5l 0,4l 0,2l 0 |
6,6 5,28 3,96 3,3 2,64 1,32 0 |
0 95,48 143,23 149,19 143,23 95,48 0 |
0 211,88 317,81 331,06 317,81 211,88 0 |
Таблица 1.5.3 – Определение пролетных моментов в неразрезном ригеле
|
Схема загружения, опорные моменты, кНм |
х, м |
х/l |
(l-x) /l |
Ординаты изгибающих моментов в крайнем (среднем) пролете, кНм | |||||||||
| Мх |
М12(23)*(l-x)/l |
M21(32)*x/l |
M* | ||||||||||
|
1+2 М12=-106 М21=-209 |
0 1,32 2,64 3,3 3,96 5,28 6,6 |
0 0,2 0,4 0,5 0,6 0,8 1 |
1 0,8 0,6 0,5 0,4 0,2 0 |
0 211,88 317,81 331,06 317,81 211,88 0 |
-106 -84,8 -63,6 -53 -42,4 -21,2 0 |
0 -41,8 -83,6 -104,5 -125,4 -167,2 -209 |
-106 85,28 170,61 173,56 150,01 23,48 -209 |
||||||
|
1+3 М12=-40 М21 =-168 |
0 1,32 2,64 3,3 3,96 5,28 6,6 |
0 0,2 0,4 0,5 0,6 0,8 1 |
1 0,8 0,6 0,5 0,4 0,2 0 |
0 95,48 143,23 149,19 143,23 95,48 0 |
-40 -32 -24 -20 -16 -8 0 |
0 -33,6 -67,2 -84 -100,8 -134,4 -168 |
-40 29,88 52,03 45,19 26,43 -46,92 -168 |
||||||
|
1+4 М12=-91 М21 =-283 |
0 1,32 2,64 3,3 3,96 5,28 6,6 |
0 0,2 0,4 0,5 0,6 0,8 1 |
1 0,8 0,6 0,5 0,4 0,2 0 |
0 211,88 317,81 331,06 317,81 211,88 0 |
-91 -72,8 -54,6 -45,5 -36,4 -18,2 0 |
0 -56,6 -113,2 -141,5 -169,8 -226,4 -283 |
-91 82,48 150,01 144,06 111,61 -32,72 -283 |
||||||
|
1+2 М23=-146 М32 =-146 |
0 1,32 2,64 3,3 3,96 5,28 6,6 |
0 0,2 0,4 0,5 0,6 0,8 1 |
1 0,8 0,6 0,5 0,4 0,2 0 |
0 95,48 143,23 149,19 143,23 95,48 0 |
-146 -116,8 -87,6 -73 -58,4 -29,2 0 |
0 -29,2 -58,4 -73 -87,6 -116,8 -146 |
-146 -50,52 -2,77 3,19 -2,77 -50,52 -146 |
||||||
|
1+3 М23=-197 М32 =-197 |
0 1,32 2,64 3,3 3,96 5,28 6,6 |
0 0,2 0,4 0,5 0,6 0,8 1 |
1 0,8 0,6 0,5 0,4 0,2 0 |
0 211,88 317,81 331,06 317,81 211,88 0 |
-197 -157,6 -118,2 -98,5 -78,8 -39,4 0 |
0 -39,4 -78,8 -98,5 -118,2 -157,6 -197 |
-197 14,88 120,81 134,06 120,81 14,88 -197 |
||||||
|
1+4 М23=-257 М32 =-175 |
0 1,32 2,64 3,3 3,96 5,28 6,6 |
0 0,2 0,4 0,5 0,6 0,8 1 |
1 0,8 0,6 0,5 0,4 0,2 0 |
0 211,88 317,81 331,06 317,81 211,88 0 |
-257 -205,6 -154,2 -128,5 -102,8 -51,4 0 |
0 -35 -70 -87,5 -105 -140 -175 |
-257 -28,72 93,61 115,06 110,01 20,48 -175 |
||||||
Перераспределение моментов под влиянием образования пластических шарниров в ригеле
Практический расчет заключается в уменьшении примерно на 30% опорных моментов ригеля М21 и М23 по схемам загружения 1+4; при этом намечается образование пластических шарниров на опоре.
К эпюре моментов схем загружения 1+4 добавляю выравнивающую эпюру моментов (приложение 1-б) так, чтобы уравнялись опорные моменты М21=М23 и были обеспечены удобства армирования опорного узла. Ординаты выравнивающей эпюры моментов:

Опорные моменты ригеля по грани колонны
На средней опоре при схеме загружения 1+4 опорный момент ригеля по грани колонны не всегда оказывается расчетным. При большой временной нагрузке и относительно малой погонной жесткости колонн он может оказаться расчетным при схемах загружения 1+2 или 1+3, то есть при больших отрицательных моментах в пролете.
Опорный момент ригеля по грани средней колонны справа М(23),1:
1) по схеме загружения 1+4 и выравненной эпюре моментов:
![]() ; (56)
; (56)
![]()

2) по схеме загружения 1+2:
![]()
Следовательно, расчетный опорный момент ригеля по грани средней опоры равен:
![]()
Опорный момент ригеля по грани крайней колонны по схеме загружения 1+4 и выравненной эпюре моментов:
![]() ; (57)
; (57)
![]()
Поперечные силы ригеля
Для расчета прочности по сечениям, наклонным к продольной оси, принимаю значения поперечных сил ригеля, большие из двух расчетов: упругого расчета и с учетом перераспределения моментов. На крайне опоре:
![]()
на средней опоре слева по схеме загружения 1+4:

На средней опоре справа по схеме загружения 1+4:

Расчет прочности ригеля по сечениям, нормальным к продольной оси
Высоту сечения подбираю по опорному моменту при ξ=0,35, поскольку на опоре момент определен с учетом образования пластического шарнира. Принятое же сечение ригеля затем проверяю по пролетному моменту так, чтобы относительная высота сжатой зоны была ξ ‹ ξу и исключалось переармированное неэкономичное сечение. При ξ=0,35, значение Ао=0,289.
Определяю рабочую высоту сечения:
 ; (58)
; (58)

h=ho+a=48+4=52 см; принимаю h=55 см.
Произвожу подбор сечений арматуры в расчетных сечениях ригеля.
Сечение в первом пролете
М=174кНм; ho=55–6=49 см; вычисляю:
 ; (59)
; (59)

По таблице III.1 (учебник В.Н. Байкова «Железобетонные конструкции) η=0,82;
 ; (60)
; (60)
 .
.
Принимаю 4Ø18 А-IVC с As=10,18см2.
Сечение в среднем пролете
М=134,06кНм.

η=0,87;

Принимаю 4Ø16 A-IVC с As=8,04см2.
Арматура для восприятия отрицательного момента в пролете устанавливается по эпюре моментов, принимаю 2Ø16 A-IVC с As=4,02см2.
Сечение на средней опоре
М=169,4кНм; ho=55–4=51 см;
![]()
η=0,845;

Принимаю 2Ø25 A-IVC с As=9,82см2.
Сечение на крайней опоре
М=99кНм;

η=0,915;
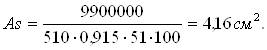
Принимаю 2Ø18 A-IVC с As=5,09см2.
Расчет прочности по сечениям, наклонным к продольной оси
Проверяю, требуется ли поперечная арматура по расчету, по первому условию:
![]() ; (61)
; (61)
![]()
230000≤286875 Н.
Проверяю, требуется ли поперечная арматура по расчету, по второму условию:
![]() ; (62)
; (62)
![]() ; (63)
; (63)
![]()
Сравниваем ![]() ; (64)
; (64)
![]()
44,1≤51,84 кН/м;
Условие выполняется, поэтому назначаю:
![]() ; (65)
; (65)
![]()
![]() ; (66)
; (66)
![]()
![]()
173773≤68850 кН.
Так как второе условие не выполняется, определяю минимальную поперечную силу, воспринимаемую бетоном сжатой зоны над наклонной трещиной:
![]() ; (67)
; (67)
![]() ; (68)
; (68)
![]() ; (69)
; (69)
![]() (70)
(70)
где N для непреднапряженных элементов равен 0;
![]()
![]() ;
;
![]()
Определяю погонное усилие в хомутах на единицу длины элемента в пределах наклонного сечения:
![]() (71)
(71)
![]()
Для обеспечения прочности по наклонному сечению на участке между соседними хомутами проверяю условия:
![]() ; (72)
; (72)

Вычисляю момент, воспринимаемый бетоном сжатой зоны над вершиной наклонного сечения:
![]() (74)
(74)
где ![]() =2;
=2;
![]()
Определяем С:
![]() (75)
(75)
![]()
Сравниваю:
![]() (76)
(76)
![]()
Вычисляю Qb, воспринимаемую бетоном сжатой зоны над расчетными наклонными сечениями:
![]() (77)
(77)
![]()
Проверяю условие:
![]() (78)
(78)
![]()
Вычисляю поперечную силу в вершине наклонного сечения:
![]() (79)
(79)
![]()
Определяю длину проекции расчетного наклонного сечения:
![]() (80)
(80)
![]()
Проверяю условия:
![]() (81)
(81)
![]()
Вычисляю поперечную силу, воспринимаемую хомутами в наклонном сечении:
![]() (82)
(82)
![]()
Проверяю условия прочности в наклонном сечении:
![]() (83)
(83)
![]()
Проверяю прочность бетона по сжатой полосе по условию:
![]() (84)
(84)
где ![]() ;
;
![]()
![]()
![]() .
.
![]()
Определение усилий в средней колонне
Определение продольных сил от расчетных нагрузок
Грузовая площадь средней колонны при сетке колонн 6,6х6,1 м2.
Постоянная
нагрузка от перекрытия одного этажа с учетом коэффициента надежности по
назначению здания ![]() , от ригеля
, от ригеля ![]() , от стойки сечением
0,3х0,3 м2 и длиной l=6 м
, от стойки сечением
0,3х0,3 м2 и длиной l=6 м ![]() .
Итого
.
Итого ![]()
Временная
нагрузка от перекрытия одного этажа с учетом ![]() ,
в том числе длительная
,
в том числе длительная ![]() ,
кратковременная
,
кратковременная ![]()
Постоянная
нагрузка от покрытия при весе кровли т плит 5 кН/м2 составит ![]() ; от ригеля – 20,74кН, от
стойки – 14,1 кН. Итого
; от ригеля – 20,74кН, от
стойки – 14,1 кН. Итого ![]()
Временная
нагрузка – снег для III снегового района при коэффициентах надежности по нагрузке ![]() и по назначению здания
и по назначению здания ![]() :
: ![]() в том числе длительная
в том числе длительная ![]() кратковременная
кратковременная ![]()
Продольная
сила колонны первого этажа рамы от длительной нагрузки ![]() ; то же, от полной нагрузки
; то же, от полной нагрузки
![]() .
.
Продольная
сила колонны подвала от длительных нагрузок ![]() ,
то же от полной нагрузки
,
то же от полной нагрузки ![]() .
.
Определение изгибающих моментов колонны от расчетных нагрузок
Вычисляю
опорные моменты ригеля перекрытия подвала – первого этажа рамы. Отношение
погонных жесткостей, вводимых в расчет ![]() .
Вычисляю максимальный момент колонн – при загружении 1+2 без перераспределения
моментов. При действии длительных нагрузок
.
Вычисляю максимальный момент колонн – при загружении 1+2 без перераспределения
моментов. При действии длительных нагрузок ![]()
![]() при действии полной
нагрузки
при действии полной
нагрузки ![]()
![]()
Разность
абсолютных значений опорных моментов в узле рамы: при длительных нагрузках ![]() при полной нагрузке
при полной нагрузке ![]()
Изгибающий
момент колонны подвала от длительных нагрузок ![]() от
полной нагрузки
от
полной нагрузки ![]()
Изгибающий
момент колонны первого этажа от длительных нагрузок ![]() от
полной нагрузки
от
полной нагрузки ![]()
Вычисляю
изгибающие моменты колонны, соответствующие максимальным продольным силам. От
длительных нагрузок ![]() изгибающие
моменты колонн подвала
изгибающие
моменты колонн подвала ![]() первого
этажа
первого
этажа ![]() От полных нагрузок
От полных нагрузок ![]() изгибающие моменты колонн
подвала
изгибающие моменты колонн
подвала ![]() первого этажа
первого этажа ![]()
Расчет прочности средней колонны
Характеристики прочности бетона и арматуры
Класс тяжелого бетона В20 и класс арматуры А-III принимаются такие же, как и для ригеля.
Колонна подвала
Две комбинации расчетных усилий:
1. ![]() , в том числе от длительных
нагрузок
, в том числе от длительных
нагрузок ![]() и соответствующий момент
и соответствующий момент ![]() , в том числе от длительных
нагрузок
, в том числе от длительных
нагрузок ![]()
2. ![]() , в том числе
, в том числе ![]() и соответствующее
загружению 1+2 значение
и соответствующее
загружению 1+2 значение ![]() , в том
числе
, в том
числе ![]() .
.
Подбор
сечений симметричной арматуры ![]() выполняю
по двум комбинациям усилий и принимаю большую площадь сечения. Анализом усилий
устанавливаю одну расчетную комбинацию и по ней выполняю подбор сечений
арматуры. Рабочая высота сечения
выполняю
по двум комбинациям усилий и принимаю большую площадь сечения. Анализом усилий
устанавливаю одну расчетную комбинацию и по ней выполняю подбор сечений
арматуры. Рабочая высота сечения ![]() ширина
b=30 см.
ширина
b=30 см.
Эксцентриситет
силы ![]()
Случайный
эксцентриситет: ![]() или
или ![]()
Поскольку
эксцентриситет силы ![]() больше
случайного эксцентриситета
больше
случайного эксцентриситета ![]() он и
принимается для расчета статически неопределимой системы.
он и
принимается для расчета статически неопределимой системы.
Значение
моментов в сечении относительно оси, проходящей через центр тяжести наименее
сжатой (растянутой) арматуры. При длительной нагрузке ![]() при полной нагрузке
при полной нагрузке ![]()
Отношение ![]() – следует учитывать
влияние прогиба колонны, где
– следует учитывать
влияние прогиба колонны, где ![]() – радиус
ядра сечения.
– радиус
ядра сечения.
Выражение для
критической продольной силы при прямоугольном сечении с симметричным
армированием ![]() (без предварительного
напряжения) с учетом, что
(без предварительного
напряжения) с учетом, что ![]() ,
принимает вид:
,
принимает вид:
 (85)
(85)
где ![]() ;
;
![]()
![]() принимаю
принимаю ![]() ;
;
![]()

Вычисляю коэффициент η по формуле:
 (86)
(86)

Значение е
равно ![]()
Определяю граничную высоту сжатой зоны по формуле:
 (87)
(87)
где ![]()

Вычисляю:
![]() (88)
(88)
![]()
![]() (89)
(89)
![]()
 (90)
(90)
где ![]()
![]()

Определяю площадь арматуры по формуле:
 (91)
(91)

Принимаю 2Ø28
А-IIIс As=12,32 см2;
![]() – для определения Ncr было принято
– для определения Ncr было принято ![]() – перерасчет можно не
делать.
– перерасчет можно не
делать.
Консоль колонны
Опорное
давление ригеля Q=213 кН; бетон класса В20, Rb=11,5МПа, ![]() арматура класса А-III, Rs=365 МПа, Rsw=290 МПа.
арматура класса А-III, Rs=365 МПа, Rsw=290 МПа.
Принимаю длину опорной площадки l=20 см при ширине ригеля lbm =25 см и проверяю условие:
![]()
Вылет консоли
с учетом зазора С=5 см составит ![]() при
этом расстояние
при
этом расстояние ![]()
Высоту
сечения консоли у грани колонны принимаю равной ![]() при
угле наклона сжатой грани
при
угле наклона сжатой грани ![]() высота
консоли у свободного края
высота
консоли у свободного края ![]() при
этом h1=20 см≈h/2=45/2=22,5 см.
рабочая высота сечения консоли
при
этом h1=20 см≈h/2=45/2=22,5 см.
рабочая высота сечения консоли ![]() Поскольку
l1=25 см<0,9ho=0,9·42=37 см,
консоль короткая.
Поскольку
l1=25 см<0,9ho=0,9·42=37 см,
консоль короткая.
Проверяю высоту сечения короткой консоли в опорном сечении по условию:
![]() (92)
(92)
![]()
![]() (93)
(93)
![]()
Q=252кН>213кН, условие удовлетворяется.
Изгибающий
момент консоли у грани колонны ![]()
Площадь сечения продольной арматуры консоли подбираю по изгибающему моменту у грани консоли, увеличенному на 25%, по формуле, принимаем η=0,9:
![]() (94)
(94)
![]()
Принимаю 2Ø14 А-III с As=3,08 см2.
Короткие
консоли высотой сечения ![]() армируются
горизонтальными хомутами и отогнутыми стержнями.
армируются
горизонтальными хомутами и отогнутыми стержнями.
Суммарное
сечение отгибов, пересекающих верхнюю половину отрезка lw, ![]() принимаю 2Ø14 A-III с Ai=4,62см2.
условие di≤25 мм соблюдается. Длина отгибов
принимаю 2Ø14 A-III с Ai=4,62см2.
условие di≤25 мм соблюдается. Длина отгибов ![]() Условие di=16 мм≤(1/15) li=19 мм также
соблюдается.
Условие di=16 мм≤(1/15) li=19 мм также
соблюдается.
Горизонтальные
хомуты принимаем Ø6 A-I. Шаг хомутов ![]() принимаю
s=10 см<15 см.
принимаю
s=10 см<15 см.
Конструирование арматуры колонны
Колонна армируется пространственными каркасами, образованными из плоских сварных каркасов. Диаметр поперечных стержней при диаметре продольной арматуры Ø28 мм и в подвале и первом этаже здания равен 8 мм; принимаю Ø8 мм А-III с шагом s=300 мм по размеру стороны сечения колонны b=300 мм, что менее 20d=20·28=560 мм. Колонна четырехэтажной рамы члениться на два элемента длиной в два этажа каждый. Стык колонн выполняется на ванной сварке выпусков стержней с обетонировкой, концы колонн усиливаются поперечными сетками. Элементы сборной колонны должны быть проверены на усилия, возникающие на монтаже от собственного веса с учетом коэффициента динамичности и по сечению в стыке.
Фундамент колонны
Сечение колонны 30х30 см. Усилия колонны у заделки в фундаменте:
1. ![]()
2. ![]()
Ввиду
относительно малых значений эксцентриситета фундамент колонны рассчитываем как
центрально загруженный. Расчетное усилие N=1498кН, усредненное
значение коэффициента надежности по нагрузке ![]() ,
нормативное усилие
,
нормативное усилие ![]()
Грунты
основания – пески пылеватые средней плотности, маловлажные, условное расчетное
сопротивление грунта Ro=0,25 МПа; бетон тяжелый класса В12,5; Rbt=0,66МПа;![]() арматура класса А-II; Rs=280МПа. Вес единицы
объема бетона фундамента и грунта на его обрезах
арматура класса А-II; Rs=280МПа. Вес единицы
объема бетона фундамента и грунта на его обрезах ![]()
Высоту фундамента предварительно принимаю равной Н=90 см; глубина заложения фундамента Н1=105 см.
Площадь подошвы фундамента определяю предварительно по формуле:
![]() (95)
(95)
![]()
Размер
стороны квадратной подошвы ![]() .
Приравниваю размер а=2,4 м. давление на грунт от расчетной нагрузки
.
Приравниваю размер а=2,4 м. давление на грунт от расчетной нагрузки ![]()
Рабочая высота фундамента из условия продавливания по выражению:
![]() (96)
(96)
![]()
Полная высота фундамента устанавливается из условий:
1. продавливания ![]()
2. заделки колонны в
фундаменте ![]()
3. анкеровки сжатой арматуры
колонны Ø22 А-III в бетоне колонны класса В20 ![]()
Принимаю окончательно фундамент высотой Н=90 см, ho=86 см – трехступенчатый (30, 30, 30 см). Толщина дна стакана 20+5=25 см.
Проверяем,
отвечает ли рабочая высота нижней ступени фундамента Ho2=30–4=26 см условию
прочности по поперечной силе без поперечного армирования в наклонном сечении,
начинающемся в сечении III–III. Для единицы ширины этого сечения (b=100 см) ![]()
![]() – условие прочности
удовлетворяется.
– условие прочности
удовлетворяется.
Расчетные изгибающие моменты в сечениях I–I и II–II по формулам:
![]()
![]()
Площадь сечения арматуры:

Принимаю нестандартную сварную сетку с одинаковой в обоих направлениях рабочей арматурой из стержней 24Ø10 А-II с Аs=18,84см2. проценты армирования расчетных сечений:
