Реферат: Методи вирішення проблем дискретного логарифмування

Методи вирішення проблем дискретного логарифмування

1. Метод Поліга-Хелмана

Метод Поліга-Хелмана запропонований в 1978 році для визначення дискретного логарифма в мультиплікативній групі поля .

Він заснований на відомій для групи факторизації порядку  групи за ступенями простих чисел

Стосовно до адитивної групи точок з генератором  порядку  маємо  Відповідно до відомої китайської теореми про залишки існує єдине натуральне число , таке що

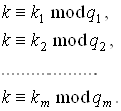
Після визначення значення  дискретний логарифм  здобувають за допомогою розширеного алгоритму Евкліда. Наведемо приклад.

Приклад 1

Нехай порядок циклічної групи  дорівнює , а точка  , тобто . Це значення має бути визначене в підсумку рішення ECDLP.

Тут  На першому етапі визначаємо точку   Отримуємо точку  другого порядку з відомими координатами  Оскільки , маємо перше порівняння

На наступному етапі знаходимо одну із точок третього порядку  Ці точки також відомі, тому з  отримуємо наступне порівняння

Нарешті, визначаємо точку 5-го порядку  й отримуємо

.

Наведені три порівняння дають єдине розв’язання  В загальному випадку необхідно знати координати  точок із загальної кількості .

Задача ускладнюється із зростанням переважно простого співмножника в розкладанні порядку  групи. У цьому зв'язку для захисту від атаки Поліга-Хелмана порядок  криптосистеми обирають рівним великому простому числу, при цьому порядок кривої  називають ² майже простим ² (з малим множником ).

2. Метод ділення точок на два

Метод ділення точок на два. Для кривих над полем  запропонований метод розв’язання , заснований на процедурі, зворотної обчисленню точки  шляхом послідовних подвоєнь і додавань при двійковому поданні числа .

У звичайній арифметиці двійкове подання цілого числа починається з визначення молодшого біта: при непарних 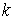 з 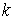 віднімається 1 (це молодший біт двійкового подання 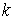) і результат ділиться на 2.

Визначимо порядок кривої як

де  - велике просте число (в існуючих криптографічних стандартах ),  - непарне число.

Нехай - точка порядку , тоді генератор криптосистеми може бути визначений як точка  порядку .

Введемо операцію ділення точки несуперсингулярної кривої

:  (1)

на два як зворотну подвоєнню. Нехай маємо точку  та точку  з координатами

 (2)

Інакше кажучи, визначення  означає знаходження координат точки  з відомої точки  Відповідно до (2) для цього необхідно вирішувати квадратне рівняння

 (3)

У загальному випадку це рівняння має два розв'язки  й  при наслідку

 (4)

Якщо слід  то точка  - непарна точка - непарне). Під час виконання (4) отримуємо дві точки:  і  ділення точки  на два з координатами

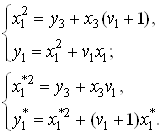 (5)

З (1) і (5) неважко отримати співвідношення між координатами точок ділення

які можуть бути корисні при криптоаналізі. Відзначимо дві властивості точок ділення.

Точки ділення пов'язані як  , де - точка другого порядку, дорівнює . Дійсно,

,

тому що

Якщо  - точка непарного порядку , тобто , то точка

ає порядок , тому що

 й .

У порівнянні з подвоєнням точки (2), яке вимагає обчислення двох множень й інверсії елемента  (найбільш трудомістка обчислювальна операція), ділення (5) не вимагає інверсії елемента й може бути реалізоване набагато швидше.

Найбільш ефективне розв’язання рівняння (3) і операцій (4), (5) виконуються в НБ (нормальному базисі) мінімальної складності, зокрема, в ОНБ (оптимальному нормальному базисі).

Розв’язання квадратного рівняння в НБ здійснюється за допомогою простої -бітової рекурентної послідовності. Слід (4) елементів парної ваги дорівнює 0, а непарної ваги - 1.

Піднесення у квадрат (добування кореня квадратного) у нормальному базисі зводиться до циклічного зсуву вправо (вліво) -бітового елемента поля.

Поряд з додаванням елементів за модулем 2 перераховані операції часто називають ²безкоштовними² і не враховують у наближених розрахунках обчислювальної складності. Ділення відповідно до (5) вимагає лише двох множень у нормальному базисі  як найбільш складних операцій. Це приблизно на порядок збільшує швидкість виконання операцій ділення на два в порівнянні з операцією подвоєння точки.

Розглянемо можливі підходи до розв’язання задач дискретного логарифма. Найбільш проста ситуація виникає для кривої

,

,  

з коефіцієнтом , порядок якої  

Максимальний простий порядок  досягається при . Покладемо, що , а генератор  має порядок . У циклічній групі  всі точки є точками подільності на два, відповідно до (4) їх -координати мають слід  й, отже, непарну вагу при поданні в НБ. При діленні на два отримуємо дві точки, одна з яких належить групі  й має порядок , а інша максимальний порядок  

Вони мають відповідно непарну й парну вагу -координат і легко розрізнюються без множення на  Вибір однієї із точок (5) порядку  здійснюється досить просто. Оскільки в групі  випливає, що

то після множення  визначається вага елемента  або його слід.

При  (парна вага елемента) користуються другою формулою (5), у протилежному випадку - першою формулою (5). Таким чином, ділення на два з вибором точки порядку  практично зводиться до двох множень у поле.

Відзначимо, що при послідовному діленні на два для половини всіх кривих (з коефіцієнтом  і порядком  достатнім виявляється лише одне множення в поле.

Для цього при кожному діленні обчислюється лише розв'язання  квадратного рівняння (4) і  координата точки ділення. Нехай , і при послідовному діленні на два з вибором точки із групи  одержуємо

.

Згідно з (5) (перша формула) , . . . , , тому підсумовуючи рівності

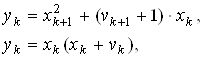
отримуємо з урахуванням першого ділення

 (6)

де кожне з рішень  вибирається так, щоб виконувалася умова  тобто в НБ вагу вектора  була непарним.

Як видно, рекурентне обчислення за формулою (6) не вимагає обчислення  координати на кожному кроці ділення, замість неї слід лише запам'ятати параметри  й . За необхідності – координата обчислюється як

Таким чином, відповідно до (6) алгоритм послідовного ділення на дві точки із групи  вимагає лише одного множення елементів у поле . Це чудова властивість операції ділення на два можна використати з метою збільшення продуктивності обчислень як при криптоаналізі, так і при швидкому експоненціюванні  будь-якої точки із групи .

Якщо припустити, що для будь-якої точки  ми знайшли спосіб визначення парності (непарності) , то послідовна процедура віднімання й ділення на два з вибором точки із групи  за поліноміальний час приведе нас до відомої точки .

Значення  у двійковому поданні визначається самою процедурою віднімання-ділення. Зрозуміло, що така функція вже не однобічна. Це питання поки залишається відкритим і  доводиться вирішувати відомими методами з експонентною складністю.

Для кривої  з коефіцієнтом  оптимальний порядок . При діленні на дві точки із групи , як й у попередньому випадку, отримуємо дві точки порядку  й , однак обидві точки ділення парні й мають слід - координат  (і, відповідно, парна вага в нормальному базисі).

Визначити, яка з них має порядок , можна шляхом множення кожної з них на , але це вимагає більших обчислювальних витрат. Більш раціональне дворазове ділення на два, яке в одній з галузей дасть дві точки порядку , вони не діляться на два й мають координати непарної ваги. Ця галузь відбраковується й залишається точка із групи

Приклад 1. Розглянемо криву Коблиця  над полем , яка має порядок . Всі точки  з генератором  наведено в таблиці 1

Таблиця 1- Координати точок  кривої  над полем

Приймемо

.

При діленні точки  на два отримаємо дві точки

 й .

Розглянемо всі операції при діленні точки відповідно до (3), (5) (друга з формул) в ОНБ із ізоморфізмом, тобто

, .

У нормальному базисі маємо . Розв’язуємо рівняння (3)

.

Відповідно до таблиці 2 , тоді одне з розв’язань для  легко отримати, задаючи перший біт, скажімо, рівним 0.

Таблиця 2 - Елементи поля  як степені елемента  в ОНБ

При цьому інші біти визначаються із суми

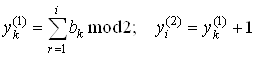, тобто

.

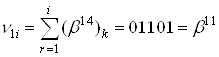Друге розв’язання, мабуть, дорівнює . Легко перевірити, що отримані розв’язання задовольняють рівняння

.

Згідно з (5) (перша з формул) і даних таблиці 2 маємо

Отримано дві точки:

  і .

Для визначення кожної необхідно виконати по два множення елементів поля. Неважко перевірити виконання умови

дискретне логарифмування метод

, ,

зокрема,

.

Обидві точки мають сліди

,

і, отже, діляться на два, але мають різні порядки. Точка  має порядок 22, а точка  - порядок Для визначення порядку достатньо виконати ще одне ділення на два. Якщо поділити точку, то отримаємо дві точки порядку 44, що не діляться на два (з непарною вагою x координат). При діленні точки  отримаємо дві точки з порядками 22 й 11 (з парною вагою x координат).