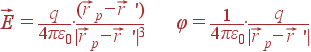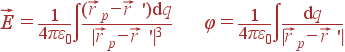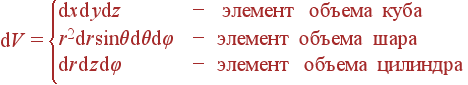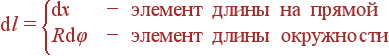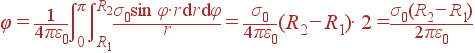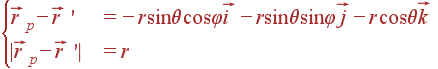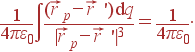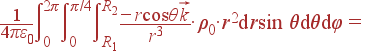Статья: Закон Кулона. Поле и потенциал распределенной системы зарядов в вакууме

М.И. Векслер, Г.Г. Зегря

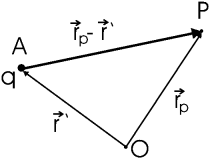
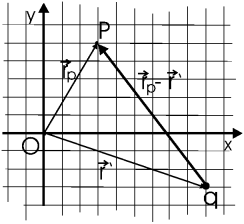
Пусть O - начало координат, P - точка, в которой ищется поле, A - точка, в которой расположен заряд q. Вектор обычно обозначают , вектор обозначают . Тогда напряженность электрического поля и потенциал, создаваемые зарядом, записываются как:

Задача. Найти поле, которое в точке создает заряд q, находящийся в точке .

Ответ:  

При наличии распределенного заряда, создающего поле, необходимо провести интегрирование:

При этом пробегает всевозможные положения из начала координат в точки, где есть заряд dq. Последний записывается как

Если рассматривается равномерно заряженная зарядом Q объемная (объема V), поверхностная (площади S) или линейная (длины L) область, то, соответственно,

Как записать dV, dS и dl? Это зависит исключительно от геометрии:

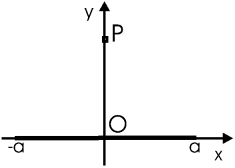
Задача. Нить, равномерно заряженная с плотностью λ0, имеет длину 2a и расположена в плоскости xy вдоль оси x симметрично относительно оси y. Найти поле на оси y как функцию y.

Ответ:  

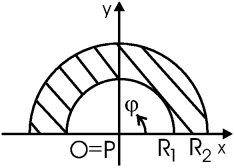
Задача. Найти потенциал в центре пластины в форме полудиска. Внутренний и внешний радиусы R1 и R2, заряд σ = σ0sinφ, где φ- угол в плоскости xy.

Решение: Потенциал рассчитываем по стандартной формуле (2):

При этом

Соответственно,

С учетом формы тела, создающего поле,

причем φ изменяется в пределах от 0 до π, а r - от R1 до R2. Теперь можно продолжить интегрирование формулы для φ:

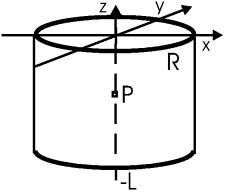
Задача. Найти поле на оси кольца радиуса R, заряженного как λ = λ0cosφ. Кольцо расположено в плоскости xy.

Ответ:  

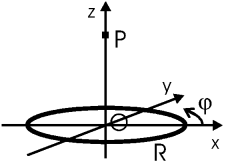
Задача. Найти потенциал на оси z цилиндрической поверхности радиуса R. Цилиндр заряжен как σ = σ0cosφ и расположен соосно с z, занимая область –L... 0.

Ответ: φ(z) = 0

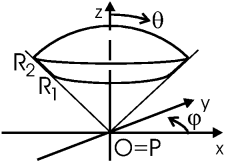
Задача. Найти поле в центре шарового сектора с внутренним и внешним радиусами R1, R2, занимающего область φ = 0... 2π, θ = 0... π/4, равномерно заряженного зарядом ρ0.

Решение: Заряженный объект (шаровой сектор) является объемным, так что

где использовано выражение для элемента объема шара. У нас начало координат совпадает с точкой, где ищется поле, так что

Вектор запишется:

При этом

Теперь у нас уже есть все составные компоненты для проведения интегрирования. Пределы интегрирования вытекают из условия задачи:

Совершенно очевидно, что члены, содержащие cosφ или sin φ, при интегрировании по φ от 0 до 2π дадут ноль (это интегрирование по периоду), поэтому их можно дальше не выписывать.

Направление вектора против оси z естественно из симметрии задачи. Если заряд положителен, то поле должно быть ориентировано от заряженного сектора, что и имеет место.

Список литературы

1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.

2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.

3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.: Наука, 1992. - 661 с.

Для подготовки данной работы были использованы материалы с сайта http://edu.ioffe.ru/r