Лабораторная работа: Анализ динамических характеристик автотракторной силовой передачи
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра: «Автомобиле - и тракторостроение»
Анализ динамических характеристик
автотракторной силовой передачи
по дисциплине: “САПР в тракторостроении”
Выполнил:
студент группы АТФ-4С
Дитковский Р.С.
Проверил:
Соколов-Добрев Н.С.
Волгоград, 2010
Введение
Нагруженность силовых передач тягово-транспортных средств в эксплуатации имеет динамический характер. Она формируется в результате действия как внешних, так и внутренних возмущений. Основными среди внешних считаются флуктуации тягового сопротивления и крутящего момента двигателя, возмущения от колебаний остова на подвеске, для гусеничных машин – от неравномерности перемотки гусеницы, а также воздействия со стороны системы управления. Основными среди внутренних считаются кинематические и силовые возмущения от перезацепления шестерен, несоосности валов, неравномерности вращения кардана, деформаций и смещений корпусных деталей.
Неравномерность действия внешних нагрузок вызывает крутильные и изгибные колебания в валопроводе силовой передачи. Их роль в процессе накопления усталостных повреждений значительна. По современным данным, до 80 % отказов в передачах обязано своим происхождением именно колебаниям.
Выполняемые в этом курсе лабораторные работы основаны на используемых в инженерной практике методах анализа динамических характеристик передач на этапе проектирования.
Лабораторная работа № 1
РЕДУЦИРОВАНИЕ МОДЕЛИ СИЛОВОЙ ПЕРЕДАЧИ И ПОЛУЧЕНИЕ В ЕЕ СПЕКТРЕ ЗАДАННЫХ СОБСТВЕННЫХ ЧАСТОТ
1.1 Исходные данные для выполнения исследований
Исследования выполняются на базе динамической модели силовой передачи трактора ВТ-100 производства ВгТЗ. Начальная динамическая модель передачи приведена на рис. 1а, редуцированная до 10 масс динамическая модель приведена на рис. 1б.

В таблице 1 приведены значения моментов инерции масс модели и жесткости их связей при включенной в КПП третьей передаче, на которой выполняется основная часть сельскохозяйственных работ.
Каждый студент для выполнения исследования получает у преподавателя задание, в соответствии с которым он должен изменить (пересчитать) величины моментов инерции масс и жесткости связей исходной 10-массовой модели на основе предложенных преподавателем коэффициентов. Пример задания для каждого студента показан в таблице 2. В соответствии с приведенными в таблице коэффициентами должны быть изменены параметры соответствующих элементов исходной модели.
Упруго-инерционные параметры динамической модели передачи
Таблица 1
| Моменты инерции масс (приведены к оси ведущего колеса) | |||
| Обозначение массы | Узел |
Момент инерции, кг×м2 |
|
|
I1 |
Двигатель и ведущие элементы муфты сцепления | 2604,8 | |
|
I2 |
Ведомые элементы муфты сцепления | 101,01 | |
|
I3 |
Карданный вал | 11,99 | |
|
I4 |
Ведущие элементы коробки передач | 94,691 | |
|
I5 |
Ведомые элементы коробки передач | 163,2 | |
|
I6 |
Главная передача | 126,95 | |
|
I7 |
Водило планетарного механизма поворота и шкив фрикциона | 11,388 | |
|
I8 |
Конечная передача и шкив остановочного тормоза |
10,422 | |
|
I9 |
Гусеничный обвод и вращающиеся детали ходовой системы | 80,64 | |
|
I10 |
Поступательно движущиеся массы трактора и плуга | 4518,2 | |
| Жесткость участков валопровода (приведена к оси ведущего колеса) | |||
| Обознач. Участка | Участок |
Жесткость связи, Н×м/рад |
|
|
С1 |
Двигатель – ведомые элементы муфты сцепления | 24960000 | |
|
С2 |
Ведомые элементы муфты – карданный вал | 427560000 | |
|
С3 |
Карданный вал – ведущие элементы коробки | 6688000 | |
|
С4 |
Ведущие – ведомые элементы коробки | 80753000 | |
|
С5 |
Ведомые элементы коробки – главная передача | 1874448000 | |
|
С6 |
Главная передача – механизм поворота | 327750000 | |
|
С7 |
Механизм поворота – конечная передача | 50596000 | |
|
С8 |
Конечная передача – ходовая система | 45009000 | |
|
С9 |
Ходовая система – массы трактора и плуга | 58380000 | |
Коэффициенты для изменения параметров элементов
Таблица 2
| Параметр |
I1 |
I2 |
I3 |
I4 |
I5 |
I6 |
I7 |
I8 |
I9 |
I10 |
||||||||
| Коэффициент | 2 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | ||||||||
| Параметр |
С1 |
С2 |
С3 |
С4 |
С5 |
С6 |
С7 |
С8 |
С9 |
|||||||||
| Коэффициент | 2 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | |||||||||
1.2 Редуцирование модели
1.2.1 Метод редуцирования
Каждый студент должен выполнить дальнейшее редуцирование 10-массовой модели до 6-массовой. Редукция модели проводится по методу Ривина и основана на замене отдельных элементарных двухмассовых колебательных систем (рис. 2а) одномассовыми (рис. 2б) путем объединения двух масс в одну и пропорционального изменения податливости связей объединенной массы.
 |
 |
 |
![]()
![]()
![]() Ik-1
Ck Ik+1 C'k-1 I'k C'k+1
Ik-1
Ck Ik+1 C'k-1 I'k C'k+1
а) б)
Рис. 2. Схемы парциальных систем
Величина момента инерции объединенной массы и новые величины жесткости ее связей рассчитываются в соответствии со следующими формулами:
![]() ,
,
 ,
,
![]() ,
,
где ![]() -
момент инерции объединенной массы;
-
момент инерции объединенной массы;
![]() - моменты инерции объединяемых масс;
- моменты инерции объединяемых масс;
![]() - крутильная жесткость связей объединенной массы;
- крутильная жесткость связей объединенной массы;
![]() - крутильная жесткость связи объединяемых масс.
- крутильная жесткость связи объединяемых масс.
При этом способе первая и последняя массы системы не участвуют в редукции - их масса не может быть распределена между другими, также и к ним не может быть добавлена масса, иначе редуцированная модель может отличаться по динамическим свойствам от нередуцированной. Таким образом, метод позволяет редуцировать модель, включающую в себя не менее трех масс.
1.2.1 Выполнение редуцирования
Редуцирование выполняется при помощи программного комплекса DASP1.
После расчета на экран выдаются новые значения момента инерции объединенной массы и жесткость ее связей с предыдущими и последующими массами, а также распечатываются значения моментов инерции масс и жесткости связей новой системы и ее парциальные частоты.
На последующем шаге для редуцирования снова выбираем массу с наивысшей парциальной частотой и повторяем операции. В результате будет получена модель, редуцированная до 6 масс. Ход редуцирования отражаем в таблице 3.
Последовательность редуцирования модели
Таблица 3
| Число | Номер массы или связи | |||||||||||||||||||||||||||||||||
| масс | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||||||||||||||||||
|
Моменты инерции масс, кг×м2 |
||||||||||||||||||||||||||||||||||
| 2604,8 | 101,01 | 11,9 | 94,691 | 163,2 | 126,95 | 11,388 | 10,422 | 80,64 | 4518,2 | |||||||||||||||||||||||||
| 10 | Крутильная жесткость связей, Н×м/рад | |||||||||||||||||||||||||||||||||
|
0,25*108 |
0,428*109 |
0,669*107 |
0,808*108 |
0,187*1010 |
0,328*109 |
0,506*108 |
0,45*108 |
0,584*108 |
||||||||||||||||||||||||||
| Парциальные частоты колебаний масс, Гц | ||||||||||||||||||||||||||||||||||
| 15,6 | 337 | 961 | 153 | 551 | 663 | 917 | 482 | 180 | 18,1 | |||||||||||||||||||||||||
|
Моменты инерции масс, кг×м2 |
||||||||||||||||||||||||||||||||||
| 2604,8 | 101,01 | 112,91 | 163,2 | 126,95 | 11,388 | 10,422 | 80,64 | 4518,2 | ||||||||||||||||||||||||||
| 9 | Крутильная жесткость связей, Н×м/рад | |||||||||||||||||||||||||||||||||
|
0,25*108 |
0,735*107 |
0,355*108 |
0,187*10 |
0,328*109 |
0,506*108 |
0,45*108 |
0,584*108 |
|||||||||||||||||||||||||||
| Парциальные частоты колебаний масс, Гц | ||||||||||||||||||||||||||||||||||
| 15,6 | 90 | 98,1 | 544 | 663 | 917 | 482 | 180 | 25,6 | ||||||||||||||||||||||||||
|
Моменты инерции масс, кг×м2 |
||||||||||||||||||||||||||||||||||
| 2604,8 | 101,01 | 112,91 | 163,2 | 126,95 | 138,388 | 80,64 | 4518,2 | |||||||||||||||||||||||||||
| 8 | Крутильная жесткость связей, Н×м/рад | |||||||||||||||||||||||||||||||||
|
0,25*108 |
0,735*107 |
0,355*108 |
0,187*1010 |
0,472*108 |
0,419*108 |
0,584*108 |
||||||||||||||||||||||||||||
| Парциальные частоты колебаний масс, Гц | ||||||||||||||||||||||||||||||||||
| 15,6 | 90 | 98,1 | 544 | 619 | 128 | 178 | 25,6 | |||||||||||||||||||||||||||
|
Моменты инерции масс, кг×м2 |
||||||||||||||||||||||||||||||||||
| 2604,8 | 101,01 | 112,91 | 163,2 | 290,15 | 80,64 | 4518,2 | ||||||||||||||||||||||||||||
| 7 | Крутильная жесткость связей, Н×м/рад | |||||||||||||||||||||||||||||||||
|
0,25*108 |
0,735*107 |
0,351*108 |
0,467*108 |
0,419*108 |
0,584*108 |
|||||||||||||||||||||||||||||
| Парциальные частоты колебаний масс, Гц | ||||||||||||||||||||||||||||||||||
| 15,6 | 90 | 97,6 | 113 | 88 | 178 | 25,6 | ||||||||||||||||||||||||||||
|
Моменты инерции масс, кг×м2 |
||||||||||||||||||||||||||||||||||
| 2604,8 | 101,01 | 112,91 | 163,2 | 290,15 | 370,79 | |||||||||||||||||||||||||||||
| 6 | Крутильная жесткость связей, Н×м/рад | |||||||||||||||||||||||||||||||||
|
0,25*108 |
0,735*107 |
0,351*108 |
0,249*108 |
0,448*108 |
||||||||||||||||||||||||||||||
| Парциальные частоты колебаний масс, Гц | ||||||||||||||||||||||||||||||||||
| 15,6 | 90 | 97,6 | 96,6 | 78 | 84 | |||||||||||||||||||||||||||||
1.3 Получение в спектре модели заданных собственных частот
1.3.1 Исследование влияния параметров элементов модели на собственные частоты
Выбираем в главном меню программного комплекса DASP1 пункт «Формирование собственного частотного спектра». Вводим параметры полученной 6-массовой модели – моменты инерции масс и жесткость связей. Рассчитываем и заносим в таблицу собственные частоты. По запросу программы вводим диапазон поиска собственных частот в 0 с шагом 0,1 Гц.
Далее выполняем исследование влияния на эти частоты параметров каждого элемента модели. Заготавливаем таблицу 4, в которую заносим рассчитанные значения параметров указанных элементов и собственные частоты, соответствующие модели с этими параметрами.
Параметры элементов модели и собственные частоты
Таблица 4
|
Моменты инерции, кг×м2 |
Собственные частоты, Гц | |||||
| Жесткость связей, Н×м/рад | 1 | 2 | 3 | 4 | 5 | |
|
I1/10 |
260,48 | 21,3 | 53,7 | 91,2 | 101,1 | 128,799 |
|
10I1 |
26048 | 11,1 | 52,1 | 87,9 | 94,6 | 128,699 |
|
I2/10 |
10,101 | 12,7 | 52,8 | 91,8 | 127,299 | 285,893 |
|
10I2 |
1010,1 | 12,7 | 31,2 | 54,5 | 92,1 | 128,099 |
|
I3/10 |
11,291 | 13,0 | 61,7 | 89,6 | 98,7 | 316,592 |
|
10I3 |
1129,1 | 10,9 | 29,1 | 82,1 | 91,3 | 108,099 |
|
I4/10 |
16,32 | 13,3 | 61,7 | 89,1 | 96,7 | 314,292 |
|
10I4 |
1632 | 9,8 | 33,3 | 85,2 | 91,7 | 105,1 |
|
I5/10 |
29,015 | 36,2 | 59,4 | 123,99 | 253,594 | 10000,05 |
|
10I5 |
2901,5 | 31,9 | 57,5 | 61,4 | 126,799 | 10000,05 |
|
I6/10 |
37,079 | 12,3 | 52,2 | 84,1 | 92,6 | 128,199 |
|
10I6 |
3707,9 | 7,9 | 51,8 | 58,4 | 91,5 | 127,199 |
|
С1/10 |
0,25*107 |
7,8 | 40,2 | 60,9 | 92,5 | 128,499 |
|
10С1 |
0,25*109 |
13,8 | 54,0 | 92,1 | 127,999 | 258,694 |
|
С2/10 |
0,735*106 |
5,0 | 48,6 | 81,7 | 91,1 | 125,599 |
|
10С2 |
0,735*108 |
15,5 | 20,0 | 74,1 | 100,2 | 163,897 |
|
С3/10 |
0,351*107 |
8,1 | 15,5 | 47,8 | 63,7 | 97,8 |
|
10С3 |
0,351*109 |
12,8 | 15,5 | 54,6 | 94,4 | 368,499 |
|
С4/10 |
0,249*107 |
8,0 | 15,5 | 29,9 | 84,2 | 120,299 |
|
10С4 |
0,249*109 |
12,8 | 15,5 | 69,2 | 107,299 | 256,594 |
|
С5/10 |
0,448*107 |
11,5 | 25,3 | 66,0 | 92,0 | 128,199 |
|
10С5 |
0,448*109 |
12,8 | 57,0 | 91,6 | 127,399 | 266,494 |
| Номинальные частоты | 12,7 | 52,2 | 88,4 | 94,9 | 128,699 |
На основе таблицы 4 строим графики, отражающие влияние изменения параметров каждого элемента на собственные частоты.







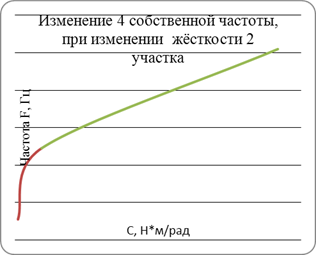





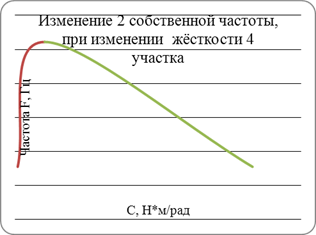


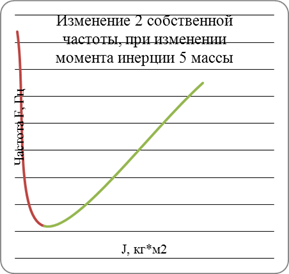



Далее за счет варьирования выбранных параметров получаем в собственном частотном спектре модели значения второй и четвертой собственных частот сначала в два раза меньшие, чем при номинальных параметрах, потом в два раза большие. Изменение параметров элементов осуществляется путем ввода их скорректированных значений. Для этого в главном меню выбирается пункт «Вносим произвольные изменения» и изменяется значение момента инерции выбранных по графикам масс и жесткость связей, оказывающих на изменение этих частот наибольшее влияние. Процесс поиска в соответствии с распечаткой должен быть отражен таблицами следующего вида (на каждом шаге изменения параметров).
Таблица 5.
| Моменты |
I1 |
I2 |
I3 |
I4 |
I5 |
I6 |
||||
|
инерции, кг×м2 |
180 | |||||||||
| Жесткость |
С1 |
С2 |
С3 |
С4 |
С5 |
|||||
| связей, Н×м/рад | ||||||||||
| Собственные | 1 | 2 | 3 | 4 | 5 | |||||
| частоты, Гц | 52 | |||||||||
Лабораторная работа № 2
АНАЛИЗ ВЛИЯНИЯ УПРУГО-ИНЕРЦИОННЫХ ПАРАМЕТРОВ ЭЛЕМЕНТОВ МОДЕЛИ СИЛОВОЙ ПЕРЕДАЧИ НА ПРОХОЖДЕНИЕ КРУТИЛЬНЫХ КОЛЕБАНИЙ ПО ВАЛОПРОВОДУ
2.1 Исходные данные и методика выполнения исследований
Для исследований используется полученная в первой части этого курса 10-массовая динамическая модель силовой передачи трактора ВТ-100 (измененная в соответствии с вариантом задания). Исследуется дополнительная динамическая нагруженность участков передачи от неравномерности действия основных эксплуатационных нагрузок. Для этого при выполнении расчетов на элементы модели прикладываем соответствующие возмущающие воздействия.
К массе I10 модели (поступательно движущиеся массы трактора и орудия, см. рис. 1) прикладываем возмущающие воздействия от неравномерности тягового сопротивления с частотой 0,1 Гц и 1 Гц. Обычно в этом частотном диапазоне помещаются нагрузки от неравномерности тягового сопротивления при выполнении трактором основной сельскохозяйственной работы - пахоты. К массе I9 модели (ведущее колесо, ходовая система и подвеска) прикладываем нагрузку с частотой 2 Гц, имитирующую воздействие от колебаний остова на подвеске, а также нагрузки с частотами 12 Гц и 24 Гц - это средние величины диапазона, в котором для данного трактора помещаются воздействия от неравномерности перемотки гусеницы при движении трактора с разными скоростями и при несинфазной работе гусеничных движителей левого и правого борта. И, наконец, приложением моментов к массе I1 имитируется воздействие на силовую передачу гармоник двигателя. Момент с частотой 30 Гц имитирует воздействие первой гармоники, с частотой 45 Гц - полуторной, с частотой 60 Гц - второй, с частотой 75 Гц - двухсполовинной, с частотой 90 Гц - третьей, с частотой 105 Гц - трехсполовинной, с частотой 120 Гц - четвертой. Все моменты, прикладываемые ко всем массам, единичные. Это позволяет при анализе результатов легко определять полученную дополнительную нагруженность участка в процентах по сравнению с величиной приложенного момента.
Для выполнения расчетов следует в главном меню программного комплекса DASP1 выбрать пункт «Считаем вынужденные колебания» и ввести запрашиваемые программой параметры элементов модели. Далее из следующего меню следует выбрать «Делаем расчет для нерезонансных частот», указать величину прикладываемого момента (1.) и номер массы, к которой он приложен (10). Программой запрашивается диапазон частот, в котором будет изменяться прикладываемый момент. Исследование для каждой из выбранных частот следует выполнить поочередно. Например, вы выбрали массу 10 и приложили к ней единичный момент, далее для нагрузки с частотой 0,1 Гц диапазон частот указывается следующим образом:
0.1,0.1
Шаг изменения частоты выбрать равным 1 Гц - ввести (1.)
После этого расчета выбрать «Считаем снова амплитуды и отношения моментов» и выполнить расчет по той же схеме для нагрузки с другой частотой.
Когда все расчеты для модели с номинальными параметрами выбраны, следует в заданное преподавателем для каждого студента число раз сначала уменьшить, потом увеличить жесткость одного из участков и выполнить для этой модели такие же исследования. После этого следует так же увеличить и уменьшить момент инерции одной из масс и повторить расчеты. Номера участков и масс для каждого студента определяет преподаватель.
| Участок | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| W (частота) | М (момент) | ||||||||
| 0,1 | 4,56E-01 | 4,48E-01 | 4,47E-01 | 4,40E-01 | 4,27E-01 | 4,17E-01 | 4,16E-01 | 4,15E-01 | 4,08E-01 |
| 1 | 4,51E-01 | 4,44E-01 | 4,43E-01 | 4,36E-01 | 4,23E-01 | 4,13E-01 | 4,12E-01 | 4,11E-01 | 4,04E-01 |
| 12 | 4,41E-01 | 4,35E-01 | 4,34E-01 | 4,28E-01 | 4,16E-01 | 4,07E-01 | 4,06E-01 | 4,05E-01 | 3,98E-01 |
| 24 | 4,79E-01 | 5,42E-01 | 5,50E-01 | 5,80E-01 | 6,30E-01 | 6,67E-01 | 6,69E-01 | 6,70E-01 | 6,67E-01 |
| 30 | 1,29E-01 | 2,42E-02 | 4,31E-02 | 1,88E-01 | 4,38E-01 | 6,31E-01 | 6,44E-01 | 6,51E-01 | 6,74E-01 |
| 45 | 1,28E-01 | 9,73E-02 | 9,34E-02 | 2,74E-02 | 9,16E-02 | 1,85E-01 | 1,91E-01 | 1,95E-01 | |
| 60 | 1,68E-02 | 4,03E-02 | 4,31E-02 | 3,07E-02 | 4,50E-03 | 1,67E-02 | 1,82E-02 | 1,91E-02 | 2,29E-02 |
| 75 | 9,81E-03 | 1,87E-02 | 2,22E-02 | 1,80E-02 | 6,24E-03 | 3,74E-03 | 4,46E-03 | 4,96E-03 | 7,13E-03 |
| 90 | 2,47E-02 | 1,23E-02 | 1,68E-02 | 1,52E-02 | 6,54E-03 | 1,33E-03 | 1,94E-03 | 2,40E-03 | 4,66E-03 |
| 105 | 4,74E-02 | 1,03E-02 | 1,74E-02 | 1,78E-02 | 8,82E-03 | 1,71E-04 | 9,77E-04 | 1,65E-03 | 5,61E-03 |
| 120 | 1,55E-01 | 1,51E-02 | 3,60E-02 | 4,45E-02 | 2,67E-02 | 4,95E-03 | 2,13E-03 | 7,31E-04 | 2,27E-02 |




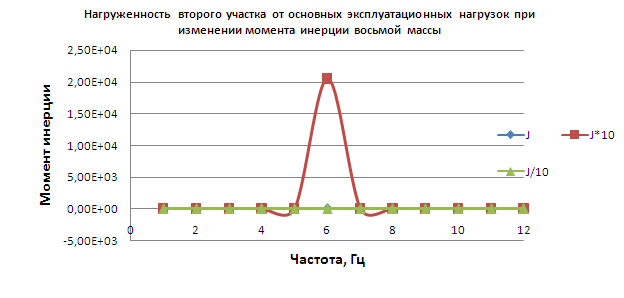
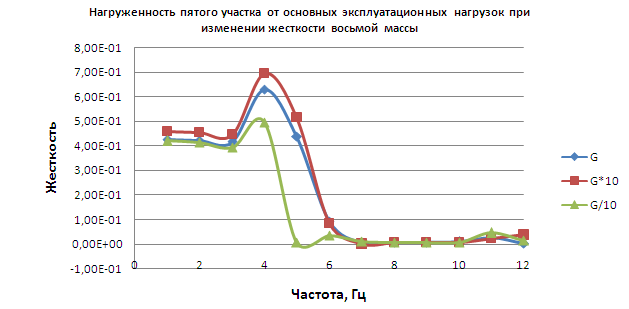
2.2 Представление и анализ результатов исследования
Результаты исследования прохождения колебаний разных частот по валопроводу силовой передачи отразим на графиках.
| Участок | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| W (частота) | М*10 | ||||||||
| 0,1 | 5,03E-01 | 4,95E-01 | 4,94E-01 | 4,86E-01 | 4,72E-01 | 4,60E-01 | 4,50E-01 | 4,49E-01 | 4,41E-01 |
| 1 | 4,89E-01 | 4,82E-01 | 4,81E-01 | 4,74E-01 | 4,62E-01 | 4,51E-01 | 4,41E-01 | 4,40E-01 | 4,33E-01 |
| 12 | 4,86E-01 | 4,80E-01 | 4,79E-01 | 4,72E-01 | 4,59E-01 | 4,49E-01 | 4,39E-01 | 4,39E-01 | 4,31E-01 |
| 24 | 1,40E-02 | 1,24E-01 | 1,41E-01 | 2,72E-01 | 5,02E-01 | 6,86E-01 | 7,06E-01 | 7,07E-01 | 7,04E-01 |
| 30 | 1,67E+00 | 1,54E+00 | 1,53E+00 | 1,04E+00 | 1,21E-01 | 6,10E-01 | 7,55E-01 | 7,64E-01 | 7,91E-01 |
| 45 | 1,84E-01 | 2,05E+04 | 2,07E-01 | 1,51E-01 | 4,30E-02 | 4,39E-02 | 6,44E-02 | 6,58E-02 | 7,02E-02 |
| 60 | 1,25E-02 | 3,91E-02 | 4,23E-02 | 3,37E-02 | 1,39E-02 | 2,12E-03 | 1,04E-02 | 1,09E-02 | 1,31E-02 |
| 75 | 1,08E-02 | 2,05E-02 | 2,43E-02 | 1,98E-02 | 6,91E-03 | 3,44E-03 | 5,68E-03 | 6,32E-03 | 9,08E-03 |
| 90 | 2,71E-02 | 1,36E-02 | 1,85E-02 | 1,66E-02 | 6,85E-03 | 1,04E-03 | 4,81E-04 | 5,95E-04 | 1,16E-03 |
| 105 | 5,16E-02 | 1,15E-02 | 1,92E-02 | 1,89E-02 | 8,07E-03 | 7,34E-04 | 1,01E-04 | 1,70E-04 | 5,80E-04 |
| 120 | 1,63E-01 | 1,71E-02 | 3,92E+03 | 4,34E-02 | 1,89E-02 | 1,18E-03 | 8,39E-05 | 2,85E-05 | 8,84E-04 |
| Участок | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| W (частота) | М/10 | ||||||||
| 0,1 | 4,41E-01 | 4,34E-01 | 4,33E-01 | 4,26E-01 | 4,13E-01 | 4,03E-01 | 4,03E-01 | 4,02E-01 | 3,95E-01 |
| 1 | 4,30E-01 | 4,24E-01 | 4,23E-01 | 4,16E-01 | 4,05E-01 | 3,96E-01 | 3,95E-01 | 3,95E-01 | 3,88E-01 |
| 12 | 4,27E-01 | 4,21E-01 | 4,20E-01 | 4,14E-01 | 4,03E-01 | 3,94E-01 | 3,94E-01 | 3,93E-01 | 3,86E-01 |
| 24 | 1,06E-02 | 5,77E-02 | 6,35E-02 | 1,07E-01 | 1,84E-01 | 2,46E-01 | 2,47E-01 | 2,51E-01 | 2,82E-01 |
| 30 | 5,82E+00 | 5,62E+00 | 5,59E+00 | 4,04E+00 | 1,14E+00 | 1,18E+00 | 1,20E+00 | 1,38E+00 | 2,75E+00 |
| 45 | 1,17E-01 | 1,37E-01 | 1,40E-01 | 1,08E-01 | 4,59E-02 | 4,14E-03 | 4,59E-03 | 8,81E-03 | 4,13E-02 |
| 60 | 8,16E-03 | 3,20E-02 | 3,49E-02 | 2,98E-02 | 1,66E-02 | 5,96E-03 | 5,85E-03 | 4,64E-03 | 5,86E-03 |
| 75 | 1,25E-01 | 1,59E-02 | 1,94E-02 | 1,93E-02 | 1,45E-02 | 1,05E-02 | 1,04E-02 | 9,17E-03 | 4,17E-03 |
| 90 | 2,03E-02 | 1,39E-02 | 1,81E-02 | 1,07E-02 | 6,56E-03 | 2,02E-02 | 2,02E-02 | 1,86E-02 | 4,64E-03 |
| 105 | 4,46E-02 | 1,04E-02 | 1,72E-02 | 1,55E-02 | 4,14E-03 | 5,04E-03 | 5,06E-03 | 4,86E-03 | 7,81E-04 |
| 120 | 1,41E-01 | 1,53E-02 | 3,45E-02 | 3,64E-02 | 1,30E-02 | 6,06E-03 | 6,13E-03 | 6,14E-03 | 6,95E-04 |
| Участок | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| W (частота) | С*10 | ||||||||
| 0,1 | 4,89E-01 | 4,82E-01 | 4,81E-01 | 4,73E-01 | 4,59E-01 | 4,47E-01 | 4,46E-01 | 4,45E-01 | 4,38E-01 |
| 1 | 4,84E-01 | 4,77E-01 | 4,76E-01 | 4,68E-01 | 4,55E-01 | 4,44E-01 | 4,43E-01 | 4,42E-01 | 4,34E-01 |
| 12 | 4,73E-01 | 4,67E-01 | 4,66E-01 | 4,59E-01 | 4,47E-01 | 4,37E-01 | 4,36E-01 | 4,35E-01 | 4,28E-01 |
| 24 | 5,65E-01 | 6,27E-01 | 6,34E-01 | 6,58E-01 | 6,95E-01 | 7,24E-01 | 7,25E-01 | 7,26E-01 | 7,23E-01 |
| 30 | 1,46E-03 | 1,64E-01 | 1,84E-01 | 3,08E-01 | 5,16E-01 | 6,81E-01 | 6,91E-01 | 6,99E-01 | 7,23E-01 |
| 45 | 6,14E-02 | 3,13E-02 | 2,75E-02 | 1,32E-02 | 8,48E-02 | 1,42E-01 | 1,45E-01 | 1,48E-01 | 1,58E-01 |
| 60 | 2,09E-02 | 4,57E-02 | 4,87E-02 | 3,30E-02 | 4,94E-04 | 2,55E-02 | 2,71E-02 | 2,86E-02 | 3,42E-02 |
| 75 | 1,02E-02 | 2,03E-02 | 2,41E-02 | 1,91E-02 | 5,74E-03 | 5,02E-03 | 5,74E-03 | 6,39E-03 | 9,18E-03 |
| 90 | 2,64E-02 | 1,33E-02 | 1,82E-02 | 1,61E-02 | 6,27E-03 | 1,68E-03 | 2,26E-03 | 2,80E-03 | 5,45E-03 |
| 105 | 5,05E-02 | 1,12E-02 | 1,88E-02 | 1,86E-02 | 8,22E-03 | 2,50E-04 | 9,99E-04 | 1,69E-03 | 5,76E-03 |
| 120 | 1,62E-01 | 1,66E-02 | 3,85E-02 | 4,45E-02 | 2,23E-02 | 4,01E-03 | 1,66E-03 | 5,63E-04 | 1,75E-02 |
| Участок | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| W (частота) | С/10 | ||||||||
| 0,1 | 4,48E-01 | 4,41E-01 | 4,40E-01 | 4,33E-01 | 4,20E-01 | 4,10E-01 | 4,09E-01 | 4,08E-01 | 4,01E-01 |
| 1 | 4,38E-01 | 4,32E-01 | 4,31E-01 | 4,25E-01 | 4,13E-01 | 4,03E-01 | 4,02E-01 | 4,01E-01 | 3,95E-01 |
| 12 | 4,11E-01 | 4,07E-01 | 4,06E-01 | 4,01E-01 | 3,92E-01 | 3,85E-01 | 3,84E-01 | 3,84E-01 | 3,77E-01 |
| 24 | 1,10E-01 | 2,18E-01 | 2,31E-01 | 3,27E-01 | 4,95E-01 | 6,28E-01 | 6,39E-01 | 6,40E-01 | 6,37E-01 |
| 30 | 1,25E+00 | 1,13E+00 | 1,11E+00 | 7,18E-01 | 8,02E-03 | 5,89E-01 | 6,37E-01 | 6,45E-01 | 6,68E-01 |
| 45 | 1,85E-01 | 2,03E-01 | 2,05E-01 | 1,47E-01 | 3,49E-02 | 5,50E-02 | 6,25E-02 | 6,38E-02 | 6,81E-02 |
| 60 | 1,17E-02 | 3,55E-02 | 3,84E-02 | 3,03E-02 | 1,16E-02 | 3,30E-03 | 4,57E-03 | 4,82E-03 | 5,76E-03 |
| 75 | 1,02E-02 | 1,80E-02 | 2,14E-02 | 1,81E-02 | 7,68E-03 | 6,90E-04 | 1,42E-03 | 1,59E-03 | 2,28E-03 |
| 90 | 2,44E-02 | 1,21E-02 | 1,66E-02 | 1,50E-02 | 6,69E-03 | 9,25E-05 | 7,09E-04 | 8,77E-04 | 1,70E-03 |
| 105 | 4,64E-02 | 1,02E-02 | 1,72E-01 | 1,72E-02 | 7,88E-03 | 2,83E-04 | 4,51E-04 | 7,64E-04 | 2,60E-03 |
| 120 | 1,65E-01 | 1,40E-02 | 3,60E-02 | 5,40E-02 | 4,61E-02 | 3,85E-02 | 3,14E-02 | 1,07E-02 | 3,31E-01 |
















Литература
Барский И.Б., Анилович В.Я., Кутьков Г.М. Динамика трактора. - М.: Машиностроение, 1973.
Вейц В.Л., Кочура А.Е., Мартыненко А.М. Динамические расчеты приводов машин. - Л.: Машиностроение, 1971.
Маслов Г.С. Расчеты колебаний валов: Справочник. - М.: Машиностроение, 1980.
Шеховцов В.В. Анализ и синтез динамических характеристик автотракторных силовых передач и средств для их испытания. Монография.- Волгоград, изд-во РПК «Политехник», 2004. – 224 с.