Курсовая работа: Дослідження функцій гіпергеометричного рівняння
Курсова робота з математики
«Дослідження функцій гіпергеометричного рівняння»
Введення
У зв'язку із широким розвитком чисельних методів і зростанням ролі чисельного експерименту у великому ступені підвищився інтерес до спеціальних функцій. Це пов'язане із двома обставинами. По-перше, при розробці математичної моделі фізичного явища для з'ясування відносної ролі окремих ефектів вихідну задачу часто доводиться спрощувати для того, щоб можна було одержати рішення в легко аналізованій аналітичній формі. По-друге, при рішенні складних задач на ЕОМ зручно використовувати спрощені задачі для вибору надійних і економічних обчислювальних алгоритмів. Дуже рідко при цьому можна обмежитися задачами, що приводять до елементарних функцій. Крім того, знання спеціальних функцій необхідно для розуміння багатьох важливих питань теоретичної й практичної фізики.
Найбільше часто вживаними функціями є так звані спеціальні функції математичної фізики: класичні ортогональні поліноми (поліноми Якоби, Лагерра, Ермита), циліндричні, сферичні й гіпергеометричні. Теорії цих функцій і їхніх додатків присвячений цілий ряд досліджень.
1. Гіпергеометричне рівняння
1.1 Визначення гіпергеометричного ряду
Гіпергеометричним рядом називається статечної ряд виду
![]()
де z – комплексна змінна, ![]() ,
, ![]() ,
, ![]() - параметри, які можуть приймати
будь-які речовинні або комплексні значення (
- параметри, які можуть приймати
будь-які речовинні або комплексні значення (![]()
![]() 0,-1,-2,…),і символ
0,-1,-2,…),і символ ![]() позначає
величину
позначає
величину
![]() =
=![]()
![]() =1
=1
Якщо ![]() й
й ![]() – нуль або ціле негативне число,
ряд обривається на кінцевому числі членів, і сума його являє собою поліном
відносно z. За винятком цього випадку, радіус збіжності гіпергеометричного ряду
рівняється одиниці, у чому легко переконатися за допомогою ознаки збіжності
Даламбера: думаючи
– нуль або ціле негативне число,
ряд обривається на кінцевому числі членів, і сума його являє собою поліном
відносно z. За винятком цього випадку, радіус збіжності гіпергеометричного ряду
рівняється одиниці, у чому легко переконатися за допомогою ознаки збіжності
Даламбера: думаючи
![]()
![]() zk
zk
маємо
![]() =
=![]()
![]()
![]() ,
,
коли k![]()
![]() , тому гіпергеометричний ряд
сходиться при
, тому гіпергеометричний ряд
сходиться при ![]() <1 і розходиться при
<1 і розходиться при ![]() >1.
>1.
Сума ряду
F(![]() ,
, ![]() ,
, ![]() ,z) =
,z) = ![]() ,
, ![]() <1 (1.1)
<1 (1.1)
називається гіпергеометричною функцією.
Дане визначення гіпергеометричної функції придатне
лише для значень z, що належать колу збіжності, однак надалі буде показано, що
існує функція комплексного змінного z, регулярна в площині з розрізом (1, ![]() ) яка при
) яка при ![]() <1
збігається з F(
<1
збігається з F(![]() ,
, ![]() ,
, ![]() ,z). Ця функція є аналітичним
продовженням F(
,z). Ця функція є аналітичним
продовженням F(![]() ,
, ![]() ,
, ![]() ,z) у розрізану площину й
позначається тим же символом.
,z) у розрізану площину й
позначається тим же символом.
Щоб виконати аналітичне продовження припустимо
спочатку що R(![]() )>R(
)>R(![]() )>0 і скористаємося
інтегральним поданням
)>0 і скористаємося
інтегральним поданням
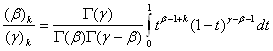 (1.2)
(1.2)
k=0,1,2,..
Підставляючи (1.2) в (1.1) знаходимо
F(![]() ,
, ![]() ,
, ![]() ,z) =
,z) = 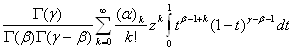 = =
= =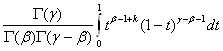
![]()
причому законність зміни порядку інтегрування й підсумовування випливає з абсолютної збіжності.
Дійсно, при R(![]() )>R(
)>R(![]() ) >0 і
) >0 і ![]() <1
<1
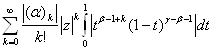
![]()
![]()
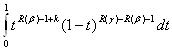
![]() =
=
=![]() F(
F(![]() , R(
, R(![]() ),R(
),R(![]() ),
),![]() )
)
На підставі відомого біноминального розкладання
![]() =(1-tz)-a(1.3)
=(1-tz)-a(1.3)
0![]() t
t![]() 1,
1,![]() <1
<1
тому для F(![]() ,
, ![]() ,
, ![]() ,z) виходить подання
,z) виходить подання
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= 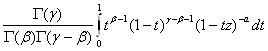 (1.4)
(1.4)
R(![]() )>R(
)>R(![]() ) >0 і
) >0 і ![]() <1
<1
Покажемо, що інтеграл у правій частині останньої
рівності зберігає зміст і представляє регулярну функцію комплексного змінного z
у площині з розрізом (1, ![]() ).
).
Для z приналежні області ![]() ,
, ![]() (R – довільно велике,
(R – довільно велике, ![]() і
і ![]() довільно малі
позитивні числа), і 0 < t < 1 підінтегральне вираження є регулярна
функція z і безперервна функція t ; тому досить показати що інтеграл сходиться
рівномірно в розглянутій області. Доказ треба з оцінки
довільно малі
позитивні числа), і 0 < t < 1 підінтегральне вираження є регулярна
функція z і безперервна функція t ; тому досить показати що інтеграл сходиться
рівномірно в розглянутій області. Доказ треба з оцінки
![]()
(М – верхня границя модуля функції (1-tz)-a, безперервної в замкнутій області
![]() ,
, ![]() , 0
, 0![]() t
t ![]() 1)
1)
що показує, збіжність інтеграла буде при R(![]() )>R(
)>R(![]() ) >0
інтеграл
) >0
інтеграл
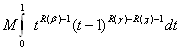 сходиться
сходиться
Таким чином, умова ![]() <1 в (1.4) може бути
відкинуто, і шукане аналітичне продовження гіпергеометричної функції в
розрізану площину дається формулою
<1 в (1.4) може бути
відкинуто, і шукане аналітичне продовження гіпергеометричної функції в
розрізану площину дається формулою
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= 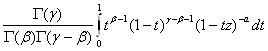 (1.5)
(1.5)
R(![]() )>R(
)>R(![]() ) >0;
) >0; ![]()
У загальному випадку, коли параметри мають довільні
значення, аналітичне продовження F(![]() ,
, ![]() ,
, ![]() ,z) площина з розміром (1,
,z) площина з розміром (1, ![]() ) може бути
отримане у формі контурного інтеграла, до якого приводить підсумовування ряду
(1.1) за допомогою теорії відрахувань.
) може бути
отримане у формі контурного інтеграла, до якого приводить підсумовування ряду
(1.1) за допомогою теорії відрахувань.
Більше елементарний метод продовження, що не дає, однак, можливість одержати в явній формі загальне аналітичне вираження гіпергеометричної функції, полягає у використанні рекурентного співвідношення (1.6)
![]() F(
F(![]() ,
, ![]() ,
, ![]() ,z) =
,z) = ![]() +
+ ![]()
справедливість якого може бути встановлена підстановкою в нього ряду (1.1). Після підстановки й приведення подібних членів коефіцієнт при zk у правій частині (1.6) буде
![]()
![]() +
+![]() -
- ![]() = =
= =![]() {
{![]()
![]() -
-![]()
![]() -
-![]() }= =
}= =![]() (
(![]()
![]()
![]()
![]()
Шляхом повторного застосування цієї тотожності можна
представити функцію F(![]() ,
, ![]() ,
, ![]() ,z) з довільними параметрами (
,z) з довільними параметрами (![]()
![]() 0,-1,-2,…)у вигляді
суми
0,-1,-2,…)у вигляді
суми
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= ![]() F(
F(![]() +s,
+s, ![]() +p,
+p, ![]() +2p, z) (1.7)
+2p, z) (1.7)
де р – ціле позитивне число ![]() (
(![]() ,
, ![]() ,
, ![]() ,z) – поліном відносно z. Якщо
вибрати число р досить більшим, так, щоб R(
,z) – поліном відносно z. Якщо
вибрати число р досить більшим, так, щоб R(![]() )>-p і R(
)>-p і R(![]() -
-![]() )>-p, то аналітичне
продовження кожної з функцій F(
)>-p, то аналітичне
продовження кожної з функцій F(![]() +s,
+s, ![]() +p,
+p, ![]() +2p, z) може бути виконане по
формулі (1.5). Підставляючи отримані вираження в (1.7) одержимо функцію,
регулярну в площині з розрізом (1,
+2p, z) може бути виконане по
формулі (1.5). Підставляючи отримані вираження в (1.7) одержимо функцію,
регулярну в площині з розрізом (1, ![]() ), що при
), що при ![]() <1 збігається із сумою
гіпергеометричного ряду (1.1) і, отже, є шуканим аналітичним продовженням.
<1 збігається із сумою
гіпергеометричного ряду (1.1) і, отже, є шуканим аналітичним продовженням.
Гіпергеометрична функція F(![]() ,
, ![]() ,
, ![]() ,z) відіграє важливу роль в
аналізі і його додатках. Введення цієї функції дає можливість одержати рішення
багатьох цікавих проблем теоретичного й прикладного характеру, до яких,
зокрема, ставиться задача конформного відображення трикутника, обмеженого
пересічними прямими або дугами окружностей, різні задачі квантової механіки й
так далі.
,z) відіграє важливу роль в
аналізі і його додатках. Введення цієї функції дає можливість одержати рішення
багатьох цікавих проблем теоретичного й прикладного характеру, до яких,
зокрема, ставиться задача конформного відображення трикутника, обмеженого
пересічними прямими або дугами окружностей, різні задачі квантової механіки й
так далі.
Велика кількість спеціальних функцій може бути
виражене через функцію F(![]() ,
, ![]() ,
, ![]() ,z), що дозволяє розглядати теорію
цих функцій як відповідні спеціальні випадки загальної теорії, даної в
справжньому пункті.
,z), що дозволяє розглядати теорію
цих функцій як відповідні спеціальні випадки загальної теорії, даної в
справжньому пункті.
1.2 Елементарні властивості гіпергеометричної функції
У справжньому розділі ми розглянемо деякі властивості гіпергеометричної функції, які безпосередньо випливають із її визначення за допомогою ряду (1.1).
1. Беручи до уваги, що члени ряду не змінюються при
перестановці параметрів ![]() і
і ![]() маємо співвідношення симетрії
маємо співвідношення симетрії
F(![]() ,
, ![]() ,
, ![]() ,z)= F(
,z)= F(![]() ,
,![]() ,
,![]() ,z), (2.1)
,z), (2.1)
2. Диференціюючи розглянутий ряд по членне, знаходимо
![]() F(
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)=![]() =
=![]() =
=
=![]() =
=![]() F(
F(![]() +1,
+1, ![]() +1,
+1, ![]() +1,z)
+1,z)
Таким чином, ![]() F(
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= ![]() F(
F(![]() +1,
+1, ![]() +1,
+1, ![]() +1,z) (2.2)
+1,z) (2.2)
3. Повторне застосування цієї формули приводить до рівностей
![]() F(
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= ![]() F(
F(![]() +m,
+m, ![]() +m,
+m, ![]() +m,z) (2.3)
+m,z) (2.3)
m=1,2,...
Покладемо надалі для скорочення запису
F(![]() ,
, ![]() ,
, ![]() ,z)= F,
,z)= F,
F(![]()
![]() 1,
1, ![]() ,
, ![]() ,z)= F(
,z)= F(![]()
![]() 1),
1),
F(![]() ,
, ![]()
![]() 1,
1, ![]() ,z)= F(
,z)= F(![]()
![]() 1),
1),
F(![]() ,
, ![]() ,
, ![]()
![]() 1,z)= F(
1,z)= F(![]()
![]() 1).
1).
Функції F(![]()
![]() 1), F(
1), F(![]()
![]() 1), F(
1), F(![]()
![]() 1) називаються суміжними з F.
1) називаються суміжними з F.
4. Ми покажемо, що F і будь-які дві суміжні функції зв'язані між собою рекурентним співвідношенням з коефіцієнтами, що є лінійними функціями змінного z. Як основні співвідношення цього типу можуть бути обрані рівності (2.4), (2.5), (2.6) відповідно.
(![]() -
-![]() -
-![]() )F+
)F+![]() (1-z)F(
(1-z)F(![]() +1)-(
+1)-(![]() -
- ![]() )F(
)F(![]() -1)=0,
-1)=0,
(![]() -
-![]() -1)F+
-1)F+![]() F(
F(![]() +1)-(
+1)-(![]() - 1)F(
- 1)F(![]() -1)=0,
-1)=0,
![]() (1-z)F-
(1-z)F-![]() F(
F(![]() -1)+(
-1)+(![]() -
- ![]() )F(
)F(![]() +1)=0.
+1)=0.
Підставляючи ряд (1.1) в (2.4) маємо (2.4)
(![]() -
-![]() -
-![]() )F+
)F+![]() (1-z)F(
(1-z)F(![]() +1)-(
+1)-(![]() -
- ![]() )F(
)F(![]() -1)=
-1)=
=(![]() -
-![]() -
-![]() )
)![]() +
+![]() (1-z)
(1-z)![]() -(
-(![]() -
-
![]() )
)![]() =
=
=![]() {(
{(![]() -
-![]() -
-![]() )
)![]() +
+![]()
![]() -(
-(![]() -
- ![]() )
)![]() -
-
![]()
![]() }zk=
}zk=
=![]() {(
{(![]() -
-![]() -
-![]() )(
)(![]() +k-1)+(
+k-1)+(![]() +k)(
+k)(![]() +k-1)-(
+k-1)-(![]() -
-![]() )(
)(![]() -1)
-1)
(![]() -k-1)k} zk=0,
-k-1)k} zk=0,
тому що
z![]()
=![]() =
=![]()
![]() =
=![]() (
(![]() +1)...(
+1)...( ![]() +k-1)
+k-1)
![]() =(
=(![]() +1)...(
+1)...( ![]() +k-1)(
+k-1)( ![]() +k)
+k)
![]() =(
=(![]() -1)
-1) ![]() (
(![]() +1)...(
+1)...( ![]() +k-2)
+k-2)
![]() =
=![]() (
(![]() +1)…(
+1)…(![]() +k-2)
+k-2)
![]() =(
=(![]() +1)…(
+1)…(![]() +k-2)(
+k-2)(![]() +k-1)
+k-1)
![]() =(
=(![]() -1)
-1)![]() (
(![]() +1).......(
+1).......( ![]() +k-3)
+k-3)
Формули (2.5) і (2.6) доводяться аналогічним способом:
(![]() -
-![]() -
-![]() )F+
)F+![]() F (
F (![]() +1)-(
+1)-(![]() - 1)F(
- 1)F(![]() -1)=
-1)=
=![]() { (
{ (![]() -
-![]() -1)
-1) ![]() +
+![]()
![]() -(
-(![]() - 1)
- 1)![]() =
=
=![]()
![]() {
{![]() -
-![]() -1 +
-1 +![]() + k-(
+ k-(![]() +k-1)}zk=0,
+k-1)}zk=0,
![]() (1-z)F-
(1-z)F-![]() F (
F (![]() -1)+(
-1)+(![]() -
- ![]() )zF(
)zF(![]() +1)=
+1)=
=![]() {
{ ![]()
![]() -
-![]()
![]() -
-![]()
![]() +(
+(![]() -
- ![]() )
)![]() }zk
}zk
=![]()
![]() {
{![]() (
(![]() + k -1)(
+ k -1)(![]() + k-1)-
+ k-1)- ![]() (
(![]() + k -1)k-
+ k -1)k-![]() (
(![]() -1)(
-1)(![]() + k-1)
+ k-1)
+(![]() -
-![]() )
)![]() k}zk=0,
k}zk=0,
З (2.4)-(2.6) і властивості симетрії (2.1) треба три інших рівності:
(![]() -
-![]() -
-![]() )F+
)F+![]() (1-z)F(
(1-z)F(![]() +1)-(
+1)-(![]() -
- ![]() )F(
)F(![]() -1)=0, (2.7)
-1)=0, (2.7)
(![]() -
-![]() -1)F+
-1)F+![]() F (
F (![]() -1)-(
-1)-(![]() - 1)F(
- 1)F(![]() -1)=0, (2.8)
-1)=0, (2.8)
![]() (1-z)F-
(1-z)F-![]() F (
F (![]() -1)+(
-1)+(![]() -
- ![]() )zF(
)zF(![]() +1)=0. (2.9)
+1)=0. (2.9)
(![]() -
-![]() -
-![]() )F+
)F+![]() (1-z)F(
(1-z)F(![]() +1)-(
+1)-(![]() -
- ![]() )F(
)F(![]() -1)=
-1)=
=![]() {(
{(![]() -
-![]() -
-![]() )
)![]() +
+![]()
![]() -
-![]()
![]() -(
-(![]() -
-
![]() )
)![]() } zk =
} zk =
=![]()
![]() {(
{(![]() -
-![]() -
-![]() )(
)(![]() +k-1)+
+k-1)+![]() (
(![]() + k -1)(
+ k -1)(![]() +k)-
+k)-![]() (
(![]() +k-1)k -(
+k-1)k -(![]() -
-![]() )(
)(![]() -
-
1)}zk=0,
(![]() -
-![]() -1)F+
-1)F+![]() F (
F (![]() -1)-(
-1)-(![]() - 1)F(
- 1)F(![]() -1)=
-1)=
=![]() {(
{(![]() -
-![]() -1)
-1) ![]() +
+![]()
![]() -(
-(![]() - 1)
- 1) ![]() } zk =
} zk =
=![]()
![]() {
{![]() -
-![]() -1+
-1+![]() (
( ![]() + k )-
+ k )- ![]() (
(![]() +k-1)}zk=0,
+k-1)}zk=0,
![]() (1-z)F-
(1-z)F-![]() F (
F (![]() -1)+(
-1)+(![]() -
- ![]() )zF(
)zF(![]() +1)=
+1)=
=![]() {
{![]()
![]() -
-![]()
![]() -
-![]()
![]() +(
+(![]() -
- ![]() )
)![]() } zk
} zk
=![]()
![]() {
{![]() (
(![]() +k-1)(
+k-1)( ![]() +k-1)-
+k-1)-![]() k(
k(![]() +k-1)-
+k-1)- ![]() (
(![]() +k-1)(
+k-1)(![]() -1)+k
-1)+k
(![]() -
-![]() )}zk=0.
)}zk=0.
Інші рекурентні співвідношення виходять із (2.4) - (2.9) шляхом виключення з відповідної пари формул загальної суміжної функції. Наприклад, комбінуючи (2.5) і (2.8) або (2.6) і (2.9) одержуємо
(![]() -
-![]() )F-
)F-![]() F (
F (![]() +1)+
+1)+![]() F(
F(![]() +1)=0 (2.10)
+1)=0 (2.10)
(![]() -
-![]() )(1-z)F+(
)(1-z)F+(![]() -
-![]() )F (
)F (![]() -1)-(
-1)-( ![]() -
-![]() )F(
)F(![]() -1)=0 (2.11)
-1)=0 (2.11)
і так далі
(![]() -
-![]() )F-
)F-![]() F (
F (![]() +1)+
+1)+![]() F(
F(![]() +1)=
+1)=
=![]() {(
{(![]() -
-![]() )
)![]() +
+![]()
![]() +
+![]()
![]() } zk=
} zk=
=![]()
![]() {
{![]() -
-![]() -
-![]() (
(![]() +k)+
+k)+ ![]() (
( ![]() +k)} zk =0.
+k)} zk =0.
(![]() -
-![]() )(1-z)F+(
)(1-z)F+(![]() -
-![]() )F (
)F (![]() -1)-(
-1)-(![]() -
-![]() )F(
)F(![]() -1)=
-1)=
=![]() {(
{(![]() -
-![]() )
)![]() -(
-(![]() -
-![]() )
)![]() +(
+(![]() -
-![]() )
)![]() -(
-(![]() -
-
![]() )
)![]() } zk=
} zk=
=![]()
![]() {(
{(![]() -
-![]() )(
)(![]() +k-1)(
+k-1)(![]() +k-1)-(
+k-1)-(![]() -
-![]() )(
)(![]() +k-1)k+(
+k-1)k+(![]() -
-![]() )(
)(![]() -1)(
-1)(![]() +k-1)-
+k-1)-
(![]() -
-![]() )(
)(![]() +k-1)(
+k-1)(![]() -1)}zk=0.
-1)}zk=0.
Крім розповсюджених рекурентних співвідношень існують
аналогічні співвідношення, що зв'язують гіпергеометричну функцію виду F(![]() ,
, ![]() ,
, ![]() ,z) з який –
або парою родинних функцій виду F(
,z) з який –
або парою родинних функцій виду F(![]() +1,
+1, ![]() +m,
+m, ![]() +n,z), де l,m,n – довільні цілі
числа.
+n,z), де l,m,n – довільні цілі
числа.
Найпростішими рекурентними співвідношеннями цього типу є
F(![]() ,
, ![]() ,
, ![]() ,z)-F(
,z)-F(![]() ,
, ![]() ,
, ![]() -1,z)=
-1,z)= ![]() F(
F(![]() +1,
+1, ![]() +1,
+1, ![]() +1,z) (2.12)
+1,z) (2.12)
F(![]() ,
, ![]() +1,
+1, ![]() ,z)- F(
,z)- F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= ![]() F(
F(![]() +1,
+1, ![]() +1,
+1, ![]() +1,z) (2.13)
+1,z) (2.13)
F(![]() ,
, ![]() +1,
+1, ![]() +1,z)- F(
+1,z)- F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= ![]() F(
F(![]() +1,
+1, ![]() +1,
+1, ![]() +2,z)(2.14)
+2,z)(2.14)
F(![]() -1,
-1, ![]() +1,
+1, ![]() ,z)- F(
,z)- F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= ![]() F(
F(![]() ,
, ![]() +1,
+1, ![]() +1,z) (2.15)
+1,z) (2.15)
До даного класу ставляться також рівність (1.6)
Формули (2.12) і (2.15) доводяться підстановкою в них ряду (1.1) або виводяться на основі вже відомих рекурентних співвідношень для суміжних функцій.
1.3 Гіпергеометричне рівняння
Помітимо, що гіпергеометрична функція u= F(![]() ,
, ![]() ,
, ![]() ,z) є
інтегралом лінійного диференціального рівняння
,z) є
інтегралом лінійного диференціального рівняння
z(1-z) ![]() +[
+[ ![]() -(
-(![]() +
+![]() +1)]
+1)] ![]() -
-![]()
![]() u=0 (2.16)
u=0 (2.16)
регулярним в околиці крапки z=0.
Рівняння (2.16) називається гіпергеометричним і включає, як окремі випадки, багато диференціальних рівнянь, що зустрічаються в додатках.
Якщо привести це рівняння до стандартної форми,
розділивши його на коефіцієнт при другій похідній, то коефіцієнти отриманого
рівняння будуть регулярними функціями змінного z в області 0<![]() <1 <1, наявними
при z=0 полюс першого порядку або звичайну крапку, залежно від значень
параметрів
<1 <1, наявними
при z=0 полюс першого порядку або звичайну крапку, залежно від значень
параметрів ![]() ,
,
![]() ,
, ![]() .
.
Із загальної теорії лінійних диференціальних рівнянь треба, що в такому випадку розглянуте рівняння повинне мати приватне рішення виду
u=zs![]()
![]() zk (2.17)
zk (2.17)
де s – належне обране число, ![]() 0, статечної ряд сходиться при
0, статечної ряд сходиться при ![]() <1
<1
u=![]()
![]() zk+s
zk+s
![]() =
=![]()
![]() (k+s)zk+s-1
(k+s)zk+s-1
![]()
![]() =
=![]()
![]() (k+s)(k+s-1)zk+s-2
(k+s)(k+s-1)zk+s-2
Підставляючи (2.17) у рівняння (2.16) знаходимо
z(1-z) ![]() (
(![]() zk+s
zk+s![]() +[
+[ ![]() -(
-(![]() +
+![]() +1)z]
+1)z] ![]() (
(![]() zk+s
zk+s![]() -
-![]()
![]()
![]()
![]() zk+s=0,
zk+s=0,
z(1-z)![]() (
(![]() zk+s-1(k+s)(k+s-1))+[
zk+s-1(k+s)(k+s-1))+[![]() -(
-(![]() +
+![]() +1)z]
+1)z]![]() (
(![]() zk+s-1(k+s))-
zk+s-1(k+s))-![]()
![]()
![]()
![]()
zk+s=
=![]() (
(![]() zk+s-1(k+s)(k+s-1))-
zk+s-1(k+s)(k+s-1))-![]() (
(![]() zk+s(k+s)(k+s-1))+
zk+s(k+s)(k+s-1))+![]() (
(![]() zk+s-1
zk+s-1![]() (k+s))-
(k+s))-
-![]()
![]() zk+s(
zk+s(![]() +
+![]() +1)(k+s))-
+1)(k+s))- ![]()
![]() zk+s
zk+s![]()
![]() =
=
=![]()
![]() zk+s-1(k+s)(k+s-1+
zk+s-1(k+s)(k+s-1+![]() )-
)-![]()
![]() zk+s(s+k+
zk+s(s+k+![]() )(s+k+
)(s+k+![]() )=0,
)=0,
звідки для визначення показника s і ![]() виходить система
рівнянь
виходить система
рівнянь
![]()
![]() s(s-1-)=0,
s(s-1-)=0,
![]() (s+k)(s+k-1+
(s+k)(s+k-1+![]() ) -
) - ![]() (s+k-1+
(s+k-1+![]() )(s+k-1+
)(s+k-1+![]() )=0,
)=0,
k=1,2,...,
перше з яких дає s=0 або s=1-![]()
Припустимо, що ![]()
![]() 0,-1,-2,…і виберемо s=0
0,-1,-2,…і виберемо s=0
Тоді для обчислення коефіцієнтів ![]() одержимо рекурентне
співвідношення
одержимо рекурентне
співвідношення
![]() =
=![]()
![]() k=1,2,…,
k=1,2,…,
звідки, якщо прийняти ![]() =1, треба
=1, треба
![]() =
=![]() k=0,1,2,…,
k=0,1,2,…,
де для скорочення запису уведене позначення
![]() =
=![]() (
(![]() +1)…(
+1)…(![]() +k-1),
+k-1),
![]() =1,k=1,2,…,
=1,k=1,2,…,
У такий спосіб перше приватне рішення рівняння (2.16)
при ![]()
![]() 0,-1,-2,…буде
0,-1,-2,…буде
u=![]() = F(
= F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= ![]()
![]() zk,
zk, ![]() <1 (2.18)
<1 (2.18)
Аналогічно, вибираючи s=1-![]() одержуємо в припущенні, що
одержуємо в припущенні, що ![]()
![]() 2,3,4,…
2,3,4,…
![]() =
=![]()
![]() k=1,2,…,
k=1,2,…,
звідки, якщо взяти ![]() =1 знаходимо
=1 знаходимо
![]() =
=![]()
k=0,1,2,...,
Таким чином, при ![]()
![]() 2,3,4,…рівняння (2.16) має друге
приватне рішення
2,3,4,…рівняння (2.16) має друге
приватне рішення
u=![]() =
= ![]()
![]()
![]() =
=![]() F(1-
F(1-![]() +
+![]() ,1-
,1-![]() +
+![]() ,2-
,2-![]() ,z), (2.19)
,z), (2.19)
![]() <1,
<1, ![]()
Якщо ![]() не є цілим числом (
не є цілим числом (![]()
![]() 0,
0,![]() 1,
1, ![]() 2,…),те обоє рішення (2.18-2.19)
існують одночасно й лінійно незалежні між собою, так, що загальне рішення
рівняння (2.17) може бути представлене у формі
2,…),те обоє рішення (2.18-2.19)
існують одночасно й лінійно незалежні між собою, так, що загальне рішення
рівняння (2.17) може бути представлене у формі
u=A F(![]() ,
, ![]() ,
, ![]() ,z)+B
,z)+B![]() F(1-
F(1-![]() +
+![]() ,1-
,1-![]() +
+ ![]() ,2-
,2- ![]() ,z), (2.20)
,z), (2.20)
де А и В довільні постійні ![]() <1,
<1, ![]()
2. Подання різних функцій через гіпергеометричну
Гіпергеометрична функція F(![]() ,
, ![]() ,
, ![]() ,z) приводиться до полінома, коли
,z) приводиться до полінома, коли ![]() =0,-1,-2,…або
=0,-1,-2,…або ![]() =0,-1,-2.
Наприклад,
=0,-1,-2.
Наприклад,
F(![]() , 0,
, 0, ![]() ,z)=
,z)= ![]()
![]() zk=
zk=![]() =1,
=1,
тому що
![]() =0(0+1)(0+2)…....(0+k-1)=0.
=0(0+1)(0+2)…....(0+k-1)=0.
F(![]() , -2,
, -2, ![]() ,z)=
,z)= ![]()
![]() zk=
zk=![]() z0+
z0+![]() z+
z+![]() z2
=
z2
=
=1-2![]() z+
z+![]() z2,
z2,
тому що
![]() =1,
=1, ![]() =-2,
=-2,
![]() =(-2)(-1)=2,
=(-2)(-1)=2, ![]() =(-2)(-1)0=0,
=(-2)(-1)0=0, ![]() =(-2)(-1)01=0
=(-2)(-1)01=0
і так далі.
Перетворення
F(![]() ,
, ![]() ,
, ![]() ,z)=(1-z
,z)=(1-z![]() F(
F(![]() -
-![]() ,
,![]() -
-![]() ,
, ![]() ,z)
,z)
![]() -
-![]() =0
=0![]()
![]() =
=![]()
показує, що гіпергеометрична функція при ![]() -
-![]() =0,-1,-2,…або
=0,-1,-2,…або ![]() -
-![]() =0,-1,-2,…виражається
через алгебраїчні функції. Зокрема,
=0,-1,-2,…виражається
через алгебраїчні функції. Зокрема,
F(![]() ,
, ![]() ,
, ![]() ,z)= (1-z
,z)= (1-z![]() ,
, ![]() (3.1)
(3.1)
Надаючи параметрам ![]() ,
, ![]() спеціальні значення, знаходимо
спеціальні значення, знаходимо
(1-z)v= F(-v, 1, 1,z)
(1-z![]() = F(
= F(![]() , 1, 1,z (3.2)
, 1, 1,z (3.2)
(1-z)n= F(-n, ![]() ,
, ![]() ,z)
,z)
n=0,1,2,...
Щоб одержати подання логарифмічної функції, скористаємося розкладанням
ln(1-z)= - ![]()
![]() =-z
=-z![]()
![]()
![]() <1
<1
звідки треба
ln(1-z)=-zF(1,1,2,z) ![]() (3.3)
(3.3)
Аналогічним образом виводяться формули для зворотних кругових функцій:
arctg z=zF(![]() ,1,
,1, ![]() ,-z2)
,-z2) ![]() (3.4)
(3.4)
arcsin z=zF(![]() ,
,![]() ,
, ![]() ,z2)
,z2) ![]()
arctg z=![]() (-1)k
(-1)k![]() =z
=z![]()
![]() =z
=z![]()
![]() =
=
=z![]()
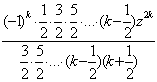 =z
=z ![]()
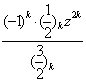 =z
=z![]()
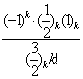 =zF(
=zF(![]() ,1,
,1, ![]() ,-z2),
,-z2),
тому що ![]() =1*2*…*k=k!
=1*2*…*k=k!
arcsinz=z+![]()
![]() =z[1+
=z[1+![]()
![]() ]=
]=
=z[1+![]()
![]() ]=z[1+
]=z[1+![]()
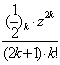 ]=z[1+
]=z[1+![]()
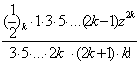 ]=
]=
=z[1+![]()
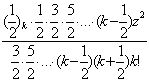 ]=z[1+
]=z[1+![]()
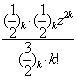 =zF(
=zF(![]() ,
,![]() ,
,![]() ,z2)...
,z2)...
3. Вироджена гіпергеометрична функція
Поряд з гіпергеометричною функцією F(![]() ,
,![]() ,
,![]() ,z), важливу роль у
теорії спеціальних функцій грає так звана Вироджена гіпергеометрична функція F(
,z), важливу роль у
теорії спеціальних функцій грає так звана Вироджена гіпергеометрична функція F(![]() ,
, ![]() ,z).
,z).
Щоб визначити цю функцію, помітимо, що статечної ряд
![]()
де z – комплексне змінне, ![]() і
і ![]() - параметри, які можуть приймати
будь-які речовинні або комплексні значення, крім
- параметри, які можуть приймати
будь-які речовинні або комплексні значення, крім ![]() =0,-1,-2,…і символ
=0,-1,-2,…і символ ![]() позначає величину
позначає величину
![]() =
=![]()
![]() =1
=1
сходиться при будь-яких кінцевих z.
Тому що, якщо позначити через ![]() загальний член ряду, те
загальний член ряду, те
![]() =
=![]()
![]() 0, коли k
0, коли k![]()
![]() .
.
Вироджена гіпергеометрична функція F(![]() ,
, ![]() ,z) визначається як сума
розглянутого ряду
,z) визначається як сума
розглянутого ряду
F(![]() ,
, ![]() ,z)=
,z)= ![]() ,
, ![]()
![]() 0,-1,-2,…,
0,-1,-2,…,![]() <
<![]() (4.1)
(4.1)
З даного визначення випливає, що F(![]() ,
, ![]() ,z) функція комплексного
змінного z.
,z) функція комплексного
змінного z.
Якщо покласти
f(![]() ,
, ![]() ,z)=
,z)= ![]() F(
F(![]() ,
, ![]() ,z)=
,z)= ![]() , (4.2)
, (4.2)
те f(![]() ,
, ![]() ,z) при фіксованому z буде цілою
функцією від
,z) при фіксованому z буде цілою
функцією від ![]() і
і ![]() . Дійсно, члени ряду (6.2) є
цілими функціями цих змінних, і ряд сходиться рівномірно в області
. Дійсно, члени ряду (6.2) є
цілими функціями цих змінних, і ряд сходиться рівномірно в області ![]() <A,
<A, ![]() <C.
<C.
Думаючи
![]() , маємо для досить більших k
, маємо для досить більших k
![]() =
=![]()
![]()
![]()
Звідси треба, що при заданому z функція F(![]() ,
, ![]() ,z)
,z)
представляє цілую функцію ![]() й мероморфну функцію
й мероморфну функцію ![]() із простими
полюсами в крапках
із простими
полюсами в крапках ![]() =0,-1,-2,…
=0,-1,-2,…
Функція F(![]() ,
,![]() ,z) досить часто зустрічається в
аналізі, причому головне її значення полягає в тому, що багато спеціальних
функцій можуть розглядатися як її окремі випадки, що значною мірою полегшує
побудову теорії цих функцій і надає їй загальний і компактний характер.
,z) досить часто зустрічається в
аналізі, причому головне її значення полягає в тому, що багато спеціальних
функцій можуть розглядатися як її окремі випадки, що значною мірою полегшує
побудову теорії цих функцій і надає їй загальний і компактний характер.
Зв'язок функції F(![]() ,
,![]() ,z) з гіпергеометричною функцією
дається співвідношенням
,z) з гіпергеометричною функцією
дається співвідношенням
![]() F(
F(![]() ,
,![]() ,z)=lim F(
,z)=lim F(![]() ,
,![]() ,
,![]() ,
,![]() ) (4.3)
) (4.3)
З визначення виродженої гіпергеометричної функції безпосередньо випливають рівності
![]() F(
F(![]() ,
,![]() ,z)=
,z)= ![]() F(
F(![]() +1,
+1,![]() +1,z) (4.4)
+1,z) (4.4)
![]() F(
F(![]() ,
,![]() ,z)=
,z)= ![]() F(
F(![]() +m,
+m,![]() +m,z) m=1,2,... (4.5)
+m,z) m=1,2,... (4.5)
і рекурентні співвідношення
(![]() -
-![]() -1)F+
-1)F+![]() F (
F (![]() +1)-(
+1)-(![]() -1)F(
-1)F(![]() -1)=0 (4.6)
-1)=0 (4.6)
![]() F-
F-![]() F(
F(![]() -1)-zF(
-1)-zF(![]() +1)=0 (4.7)
+1)=0 (4.7)
(![]() -1+z)F+(
-1+z)F+(![]() -
-![]() )F(
)F(![]() -1)-(
-1)-( ![]() -1)F(
-1)F(![]() -1)=0 (4.8)
-1)=0 (4.8)
![]() (
(![]() +z)F-
+z)F-![]()
![]() F(
F(![]() +1)-(
+1)-( ![]() -
- ![]() )zF(
)zF(![]() +1)=0 (4.9)
+1)=0 (4.9)
(![]() -
-![]() )F(
)F(![]() -1)+(2
-1)+(2![]() -
-![]() +z)F-
+z)F-![]() F(
F(![]() +1)=0 (4.10)
+1)=0 (4.10)
![]() (
(![]() -1)F(
-1)F(![]() -1)-
-1)- ![]() (
(![]() -1+z)F+(
-1+z)F+(![]() -
-![]() )zF(
)zF(![]() +1)=0 (4.11)
+1)=0 (4.11)
єднальну функцію F![]() F(
F(![]() ,
,![]() ,z) із двома будь-якими суміжними
функціями
,z) із двома будь-якими суміжними
функціями
F(![]()
![]() 1)
1) ![]() F(
F(![]()
![]() 1,
1,![]() ,z) і F(
,z) і F(![]()
![]() 1)
1) ![]() F(
F(![]() ,
,![]()
![]() 1,z)
1,z)
Формули (4.6) і (4.7) доводяться шляхом підстановки ряду (4.1) інші рекурентні співвідношення виходять із них у результаті простих алгебраїчних операцій.
(![]() -
-![]() -1)F+
-1)F+![]() F (
F (![]() +1)-(
+1)-(![]() -1)F(
-1)F(![]() -1)=
-1)=
=![]() {(
{(![]() -
-![]() -1)
-1) ![]() +
+![]()
![]() -(
-(![]() -1)
-1) ![]() }zk=
}zk=
=![]()
![]() {
{![]() -
-![]() -1+
-1+![]() (
(![]() +k)-
+k)- ![]() (
(![]() +k-1)} zk=
+k-1)} zk=
= ![]()
![]() {
{![]() -
-![]() -1+
-1+![]() +k-
+k- ![]() -k+1)} zk=0
-k+1)} zk=0
![]() F-
F-![]() F(
F(![]() -1)-zF(
-1)-zF(![]() +1)=
+1)=
=![]() {
{![]()
![]() -
-![]()
![]() -
-![]() } zk=
} zk=
=![]()
![]() {
{![]() (
(![]() +k-1)-
+k-1)-![]() (
( ![]() -1)-k
-1)-k![]() } zk=
} zk=
= ![]()
![]() {
{![]()
![]() +
+![]() k-
k-![]() -
-![]()
![]() -
-![]() -k
-k![]() } zk=0.
} zk=0.
Повторне застосування рекурентних формул приводить до
лінійних співвідношень, що зв'язують функцію F(![]() ,
,![]() ,z) з родинними функціями F(
,z) з родинними функціями F(![]() +m,
+m,![]() +n,z), де m,n-
задані цілі числа. Прикладами подібних співвідношень можуть служити рівності:
+n,z), де m,n-
задані цілі числа. Прикладами подібних співвідношень можуть служити рівності:
F(![]() ,
,![]() ,z) = F(
,z) = F(![]() +1,
+1,![]() ,z)-
,z)- ![]() F(
F(![]() +1,
+1,![]() +1,z) (4.12)
+1,z) (4.12)
F(![]() ,
,![]() ,z)=
,z)= ![]() F(
F(![]() ,
,![]() +1,z) +
+1,z) + ![]() F(
F(![]() +1,
+1,![]() +1,z) (4.13)
+1,z) (4.13)
4. Диференціальне рівняння для виродженої гіпергеометричної функції. Вироджена гіпергеометрична функція другого роду
Покажемо, що вироджена гіпергеометрична функція є приватним рішенням диференціального рівняння
z ![]() +(
+(![]() -z)
-z) ![]() -
-![]() u=0 (5.1)
u=0 (5.1)
де ![]()
![]() 0,-1,-2,…
0,-1,-2,…
u=F(![]() ,
,![]() ,z)=
,z)=![]()
![]() zk
zk
![]() =
=![]()
![]() zk-1
zk-1
![]()
![]() =
=![]()
![]() zk-2
zk-2
Дійсно, позначаючи ліву частину рівняння l(u) і полога
u= ![]() = F(
= F(![]() ,
,![]() ,z), маємо
,z), маємо
l(![]() ) =
) = ![]()
![]() zk-2+(
zk-2+(![]() -z)
-z) ![]()
![]() zk-1-
zk-1-![]()
![]()
![]() zk=
zk=
=[![]()
![]() -
-![]() ]+
]+![]()
![]() [k
[k![]() +
+![]()
![]() -k-
-k-![]() ]
]![]() 0.
0.
Щоб одержати друге лінійне незалежне рішення
розглянутого рівняння, припустимо, що ![]() , і виконаємо підстановку
, і виконаємо підстановку ![]() .
.
Рівняння (5.1) перетвориться тоді в рівняння того ж виду
z ![]() +(
+(![]() -z)
-z) ![]() -
-![]()
![]() =0
=0
с новими значеннями параметрів ![]() =1+
=1+![]() ,
, ![]() =2-
=2-![]() . Звідси треба, що при
. Звідси треба, що при ![]()
![]() 2,3,…функція також є
рішенням рівняння (5.1).
2,3,…функція також є
рішенням рівняння (5.1).
Якщо ![]()
![]() 0,
0, ![]() 1,
1, ![]() 2,…обоє рішення (
2,…обоє рішення (![]() ) мають сенс і лінійно
незалежні між собою, тому загальний інтеграл рівняння (5.1) може бути
представлений у вигляді
) мають сенс і лінійно
незалежні між собою, тому загальний інтеграл рівняння (5.1) може бути
представлений у вигляді
u= F(![]() ,
,![]() ,z)+B
,z)+B![]() F(1+
F(1+![]() -
-![]() ,2-
,2-![]() ,z) (при
,z) (при ![]() =1 u=
=1 u= ![]() ) (5.2)
) (5.2)
![]()
![]() 0,
0, ![]() 1,
1, ![]() 2,…
2,…![]()
Щоб одержати вираження загального інтеграла у формі,
придатної для будь-яких значень (крім ![]() =0,-1,-2,…), краще увести вироджену
гіпергеометричну функцію другого роду
=0,-1,-2,…), краще увести вироджену
гіпергеометричну функцію другого роду
G![]() ,
,![]() ,z)=
,z)=![]() F(
F(![]() ,
,![]() ,z)+
,z)+ ![]()
![]() F(1+
F(1+![]() -
-![]() ,2-
,2-![]() ,z)(5.3)
,z)(5.3)
![]()
![]() 0,
0, ![]() 1,
1, ![]() 2,…
2,…![]()
Формула (5.3) визначає функцію G![]() ,
,![]() ,z) для будь-яких
,z) для будь-яких ![]() , відмінних від
цілого числа. Покажемо, що при
, відмінних від
цілого числа. Покажемо, що при ![]()
![]() n+1 (n=0,1,2,…)права частина (5.3)
прагнути до певної межі. Для доказу замінимо гіпергеометричні функції
відповідними рядами й скористаємося співвідношенням теорії Г-Функції. Тоді
одержимо (5.4)
n+1 (n=0,1,2,…)права частина (5.3)
прагнути до певної межі. Для доказу замінимо гіпергеометричні функції
відповідними рядами й скористаємося співвідношенням теорії Г-Функції. Тоді
одержимо (5.4)
G![]() ,
,![]() ,z)=
,z)=![]() [
[![]()
![]()
![]() -
-![]()
![]()
![]() ]=
]=
=![]() (
(![]() )
)
Ми маємо
![]() =
=![]()
![]()
![]() =
=![]()
![]()
![]()
n=0,1,2,…![]()
![]() =
=![]()
![]()
![]() =
=![]()
![]()
![]() =
=
=![]()
![]()
![]() ,
,
тому вираження в правій частині (5.4) при ![]()
![]() n+1 приймає невизначений
вид і прагне до межі, значення якого може бути знайдене за правилом Лопиталя.
Відповідно до цього результату покладемо
n+1 приймає невизначений
вид і прагне до межі, значення якого може бути знайдене за правилом Лопиталя.
Відповідно до цього результату покладемо
G(![]() ,
,![]() ,z)=
,z)= ![]() G
G![]() ,
,![]() ,z)= (-1)n+1[
,z)= (-1)n+1[![]() ] (5.5)
] (5.5)
n=0,1,2,…![]()
Виконавши обчислення, знаходимо:
![]() =
=![]()
![]() [
[![]() ],
],
![]() =
=![]()
![]() [
[![]() ]+
]+
+![]()
![]() ,
,
звідки для G(![]() ,n+1,z) виходить явне вираження у
формі ряду (5.6)
,n+1,z) виходить явне вираження у
формі ряду (5.6)
G(![]() ,n+1,z)=
,n+1,z)= ![]()
![]()
![]() [
[![]() ]+
]+
+![]()
![]() ,
,
n=0,1,2,…,![]()
![]() 0,-1,-2,…,
0,-1,-2,…,![]()
Тут ![]() - логарифмічна похідна Г-Функція,
і для випадку n=0 порожня сума
- логарифмічна похідна Г-Функція,
і для випадку n=0 порожня сума ![]() приймається рівної 0.
приймається рівної 0.
Якщо ![]() =-m (m=0,1,2,…),те граничний
перехід
=-m (m=0,1,2,…),те граничний
перехід ![]()
![]() n+1 (n=0,1,2…)у
формулі (5.3) приводить до вираження
n+1 (n=0,1,2…)у
формулі (5.3) приводить до вираження
G(-m,n+1,z)= ![]() F(-m,n+1,z), (5.7)
F(-m,n+1,z), (5.7)
m=0,1,2,... , n=0,1,2,...
З (5.3) безпосередньо треба, що Вироджена гіпергеометрична функція другого роду задовольняє функціональному співвідношенню
G(![]() ,
,![]() ,z)=
,z)= ![]() G(
G(![]() -
-![]() +1,2-
+1,2-![]() ,z),
,z), ![]() (5.8)
(5.8)
На підставі цієї формули можна визначити функцію G(![]() ,
,![]() ,z) при
,z) при ![]() , рівному нулю
або цілому негативному числу, за допомогою рівності
, рівному нулю
або цілому негативному числу, за допомогою рівності
G(![]() ,1-n,z)=
,1-n,z)= ![]() G(
G(![]() ,
,![]() ,z)= zn G(
,z)= zn G(![]() +n,n+1,z) (5.9)
+n,n+1,z) (5.9)
n=1,2,…,![]()
Таким чином, функція має сенс при будь-яких значеннях
її параметрів. З донного визначення випливає, що G(![]() ,
,![]() ,z) регулярна функція від z у
площині з розрізом (-
,z) регулярна функція від z у
площині з розрізом (-![]() ,0) і ціла функція
,0) і ціла функція ![]() й
й ![]() .
.
Покажемо, що функція G(![]() ,
,![]() ,z) є рішенням диференціального
рівняння (5.1).
,z) є рішенням диференціального
рівняння (5.1).
При ![]()
![]() 0,
0, ![]() 1,
1, ![]() 2,…доказ треба безпосередньо з
(5.3). Для цілих
2,…доказ треба безпосередньо з
(5.3). Для цілих ![]() необхідний результат може бути
обґрунтований шляхом застосування принципу аналітичного продовження.
необхідний результат може бути
обґрунтований шляхом застосування принципу аналітичного продовження.
Якщо ![]()
![]() 0,
0, ![]() 1,
1, ![]() 2,…інтеграли F(
2,…інтеграли F(![]() ,
,![]() ,z) і G(
,z) і G(![]() ,
,![]() ,z) лінійно незалежні
між собою, у чому легко переконатися, склавши вронскиан цієї пари рішень.
,z) лінійно незалежні
між собою, у чому легко переконатися, склавши вронскиан цієї пари рішень.
З (5.1) треба W{F,G}=C![]() ez. Порівнюючи обидві
частини цієї рівності при z
ez. Порівнюючи обидві
частини цієї рівності при z![]() 0, знаходимо
0, знаходимо
C=![]()
W{ F(![]() ,
,![]() ,z),G(
,z),G(![]() ,
,![]() ,z)}= -
,z)}= - ![]()
![]() ez (5.10)
ez (5.10)
![]()
![]() 0, -1, -2,…,
0, -1, -2,…,![]()
Загальний інтеграл рівняння (7.1) у цьому випадку може бути представлений у формі
u = AF(![]() ,
,![]() ,z)+BG(
,z)+BG(![]() ,
,![]() ,z) (5.11)
,z) (5.11)
![]() ,
,![]()
![]() 0, -1, -2,…,
0, -1, -2,…,![]()
Функція G(![]() ,
,![]() ,z) володіє рядом властивостей,
аналогічних властивостям функції F(
,z) володіє рядом властивостей,
аналогічних властивостям функції F(![]() ,
,![]() ,z). Так, наприклад, мають місце
формули диференціювання:
,z). Так, наприклад, мають місце
формули диференціювання:
![]() G(
G(![]() ,
,![]() ,z)= -
,z)= - ![]() G(
G(![]() +1,
+1,![]() +1,z)
+1,z)
![]() G(
G(![]() ,
,![]() ,z)= (-1)m
,z)= (-1)m![]() G(
G(![]() +m,
+m,![]() +m,z) (5.12)
+m,z) (5.12)
m=1,2,...
рекурентні співвідношення:
G-![]() G(
G(![]() +1)-G(
+1)-G(![]() -1)=0, (5.13)
-1)=0, (5.13)
(![]() -
-![]() )G+G(
)G+G(![]() -1) -zG(
-1) -zG(![]() +1)=0, (5.14)
+1)=0, (5.14)
(![]() -1+z)G - G(
-1+z)G - G(![]() -1)+(
-1)+( ![]() -
-![]() +1)G(
+1)G(![]() -1)=0, (5.15)
-1)=0, (5.15)
(![]() +z)G+
+z)G+![]() (
(![]() -
-![]() -1)G(
-1)G(![]() +1)-zG(
+1)-zG(![]() +1)=0, (5.16)
+1)=0, (5.16)
G(![]() -1)+(2
-1)+(2![]() -
-![]() +z)G +
+z)G + ![]() (
( ![]() -
-![]() +1)G(
+1)G(![]() +1)=0, (5.17)
+1)=0, (5.17)
(![]() -
-![]() -1)G(
-1)G(![]() -1)- (
-1)- (![]() -1+z)G + zG(
-1+z)G + zG(![]() +1)=0, (5.18)
+1)=0, (5.18)
G![]() G(
G(![]() ,
,![]() ,z), G(
,z), G(![]()
![]() 1)
1) ![]() G(
G(![]()
![]() 1,
1,![]() ,z), G(
,z), G(![]()
![]() 1)
1) ![]() G(
G(![]() ,
,![]()
![]() 1,z)
1,z)
і так далі.
Справедливість цих формул випливає з визначення функції G і відповідних властивостей функції F.
5. Подання різних функцій через вироджені гіпергеометричні функції
Як ми вже відзначали, багато елементарних і
спеціальних функцій, що зустрічаються в аналізі, можуть бути вироджені через
функцію F(![]() ,
,![]() ,z).
,z).
Ми маємо, наприклад,
1) F(![]() ,
,![]() ,z)=
,z)= ![]() =
=![]()
тому що
![]()
F(1,2,z)= ![]() =
=![]() ,
,
тому що
![]()
![]()
3) F(-2,1,z)= ![]()
Висновок
Курсова робота присвячена дослідженню гіпергеометричних функцій. Можна зробити висновок:
Гіпергеометричні функції застосовуються в різних розділах математичного аналізу, зокрема, при рішенні диференціальних рівнянь і при розгляді інших спеціальних функцій.
За допомогою гіпергеометричних функцій виражаються не тільки сферичні, еліптичні, але й ряд інших, у тому числі й елементарні функції.
У роботі розглянуті визначення гіпергеометричного ряду й гіпергеометричної функції, доведені деякі елементарні властивості гіпергеометричної функції, функціональні й спеціальні функціональні співвідношення, подання різних функцій через гіпергеометричну, вироджену функція 1 і 2 роди, диференціальне рівняння для виродженої гіпергеометричної функції і його інтеграли, подання різних функцій через вироджені гіпергеометричні функції.
Література
1. Балк М.Б. Математичний аналіз: теорія аналітичних функцій. – К., 2000
2. Гурвиц А.І., Теорія функцій. – К., 2004
3. Евграфов М.О. Аналітичні функції. – К., 2003
4. Лебедєв І.І. Спеціальні функції і їхні додатки. – К., 2000
5. Маркушевич. М.М. Введення в теорію аналітичних функцій. – К., 1999
6. Смирнов В.И. Курс вищої математики тім 3,4. – К., 2005
7. Уиттекер І, Ватсон У. Курс сучасного аналізу тім 1,2. – К., 2000
8. Фихтенгольд К. Курс диференціального й інтегрального вирахування. – К., 2004
9. Фильчаков М. Довідник по вищій математиці. – К., 2000