Курсовая работа: Сортування даних - пірамідальне сортування
Зміст
Постановка задачі
Теоретичні відомості
Вхідні – вихідні дані
Математичний розв’язок
Схема алгоритму програми
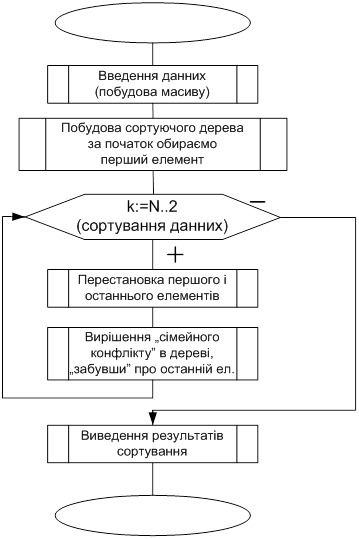
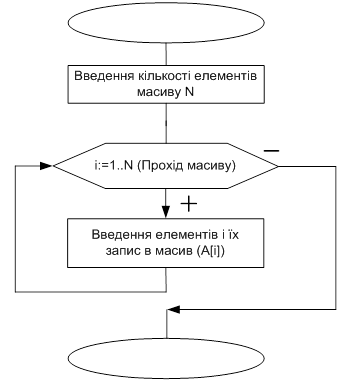
Алгоритм процедури введення даних
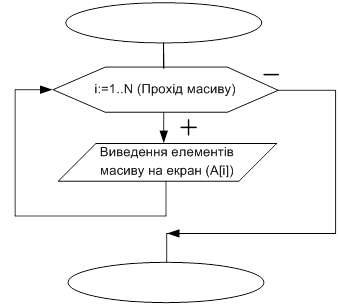
Алгоритм процедури виведення результатів сортування
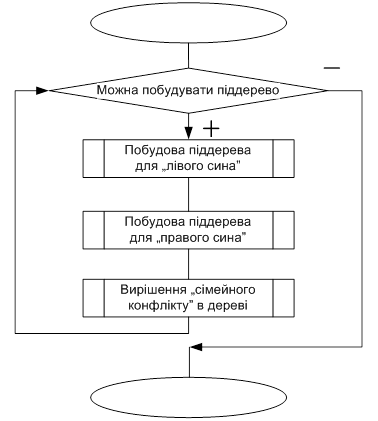
Алгоритм процедури побудови дерева
Алгоритм процедури перестановки елементів
Алгоритм процедури «вирішення сімейного конфлікту»
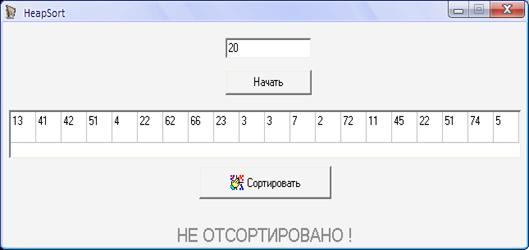
Контрольний приклад для масиву з 20 елементів
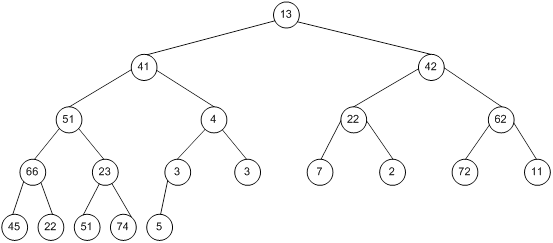
Побудова піраміди
Сортування
Опис використаних в реалізації методу процедур та функцій
Користувацьке вікно ( форма )
Текст програми
Список використаної літератури
Постановка задачі
Відсортувати масив з 20 елементів, використовуючи пірамідальне сортування.
Теоретичні відомості
Сортування даних – це обробка інформації , в результаті якої її елементи розташовуються в заданій послідовності , в залежності від значення деяких ознак елементів цієї інформації.
Найбільш поширеним видом сортування є впорядкування масиву.
Задача сортування полягає в перестановці елементів послідовності в визначеному порядку. Впорядкування здійснюється в процесі багаторазового перегляду вхідного масиву. Методи сортування діляться на два класи :
1) Внутрішнє сортування, коли працюють з даними в оперативній пам’яті з довільним доступом;
2) Зовнішнє сортування , коли впорядковують інформацію, розташовану на зовнішніх носіях.
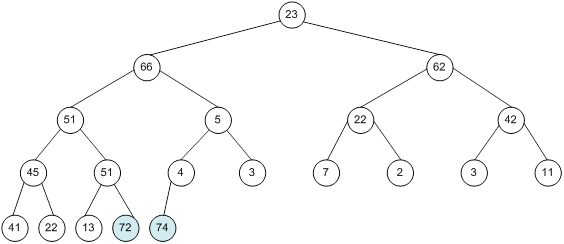
Алгоритм пірамідального сортування HeapSort використовує представлення масиву у виді дерева. Цей алгоритм не вимагає допоміжних масивів, сортуючи “на місці”. Розглянемо спочатку метод представлення масиву у виді дерева:
Нехай A[1 .. n] - деякий масив. Зіставимо йому дерево, використовуючи наступні правила:
1. A[1] - корінь дерева ;
2. Якщо A[i] - вузол дерева і 2i , то A[2*i] - вузол - “лівий син” вузла A[i]
3. Якщо A[i] - вузол дерева і 2i + 1 , то A[2*i+1] - вузол - “правий син” вузла A[i]
Правила 1-3 визначають у масиві структуру дерева, причому глибина дерева не перевершує [log2 n] + 1. Вони ж задають спосіб руху по дереву від кореня до листків. Рух вгору задається правилом 4:
4. Якщо A[i] - вузол дерева та i > 1, то A[i mod 2] - вузол - “батько” вузла A[i];
Вхідні – вихідні даніДля роботи з даною програмою та алгоритму пірамідального сортування взагалі, нам необхідно ввести елементи масиву визначеної довжини, який необхідно відсортувати.
В результаті роботи програми ми отримаємо відсортований масив введених елементів.
| Вхідні дані | Вихідні дані |
|
Розмір вхідного масиву «N» Масив з «N» елементів, елементи – цілі числа ( Масив A[1..N] – невпорядкований ). |
Впорядкований масив з «N» елементів, елементи – цілі числа , кожен елемент масиву більше або дорівнює попередньому (Масив A[1..N] ; A[i]<= A[i+1]). |
Алгоритм пірамідального сортування працює в два етапи:
I. Побудова сортуючого дерева;
II. Просіювання елементів по сортуючому дереву.
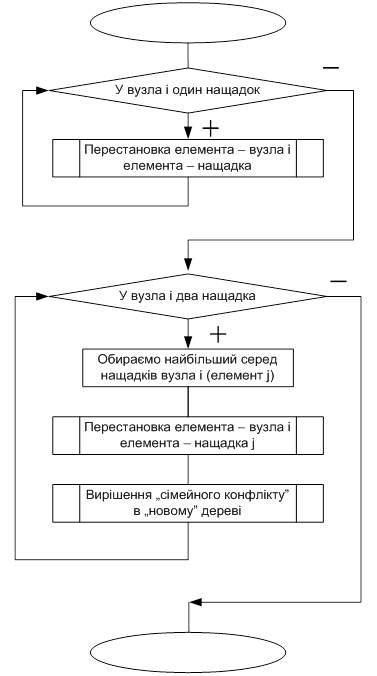
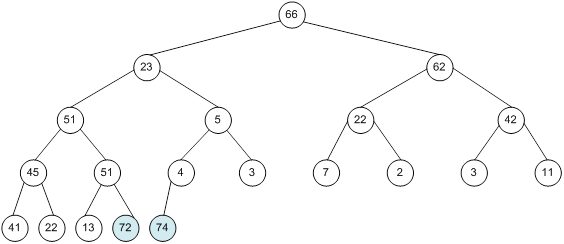
Як на I-ому, так і на II-ому етапах елементарна дія алгоритму полягає в вирішенні сімейного конфлікту: якщо найбільший із синів більше, ніж батько, то переставляються батько і цей син (процедура Swap).
У результаті перестановки може виникнути новий конфлікт у тому трикутнику, куди переставлений батько. У такий спосіб можна говорити про конфлікт (роду) у піддереві з коренем у вершині i. Конфлікт роду вирішується послідовним вирішенням сімейних конфліктів проходом по дереву вниз. Конфлікт роду вирішено, якщо прохід закінчився (i > n div 2), або ж в результаті перестановки не виник новий сімейний конфлікт (процедура Conflict).
I етап – побудова сортуючого дерева - оформимо у виді рекурсивної процедури, використовуючи визначення:
Якщо ліве і праве піддерева ( T[2i] і T[2i+1] ) дерева T[i] є сортуючими, то для перебудови T[i] необхідно вирішити конфлікт роду в цьому дереві.
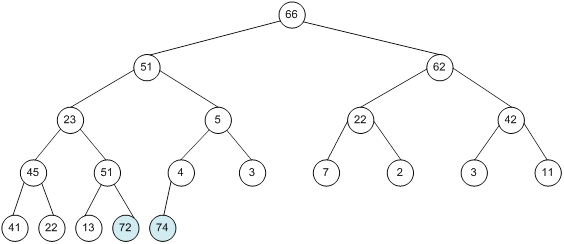
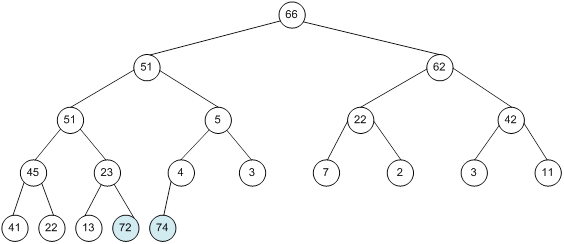
II етап - етап просіювання - для k від n до 2 повторюються наступні дії:
1.Переставити A[1] і A[k];
2.Побудувати сортуюче дерево початкового відрізка масиву A[1..k-1], усунувши конфлікт роду в корені A[1]. Відзначимо, що 2-а дія вимагає введення в процедуру Conflict параметра k.
Нескладно підрахувати, що С(n) = O( n log2 n ), М(n) = O( n log2 n )
Схема алгоритму програми
Алгоритм процедури введення даних
Алгоритм процедури виведення результатів сортування
Алгоритм процедури побудови дерева
Алгоритм процедури перестановки елементів
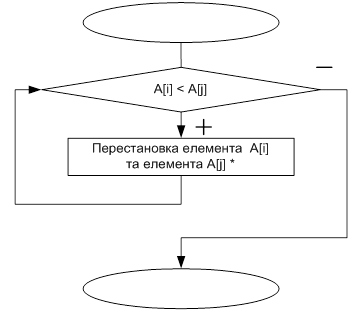
b = a[i]
a[i] = a[j]
a[j] = b
Алгоритм процедури «вирішення сімейного конфлікту»
Контрольний приклад для масиву з 20 елементів
Побудова піраміди
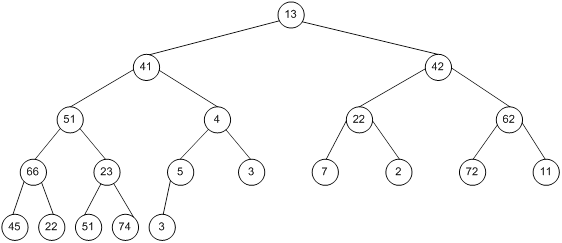
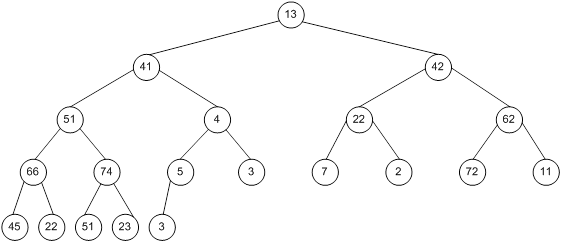
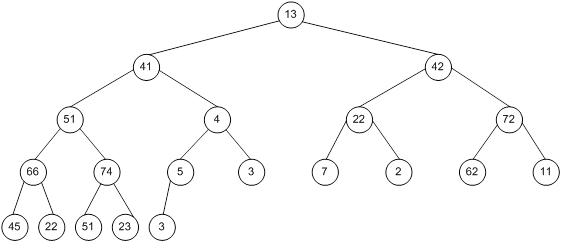

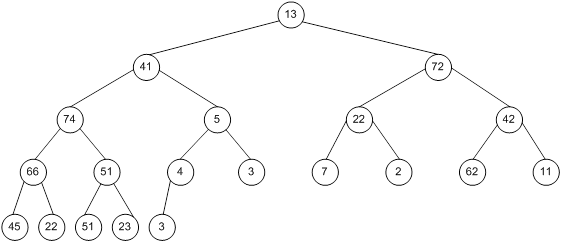
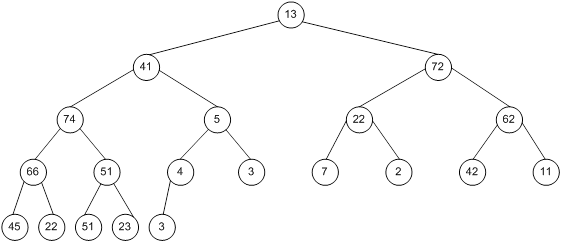
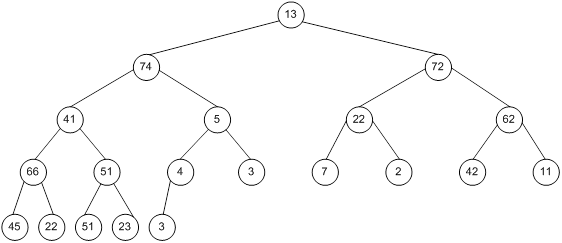
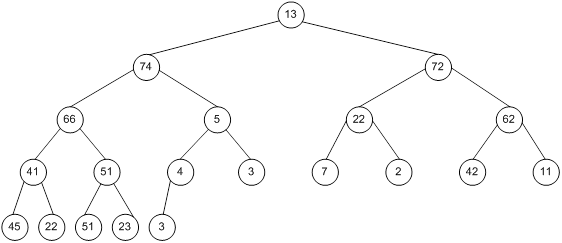
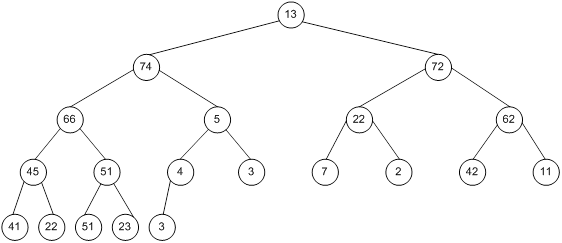
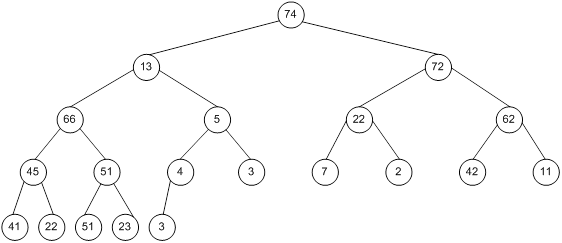
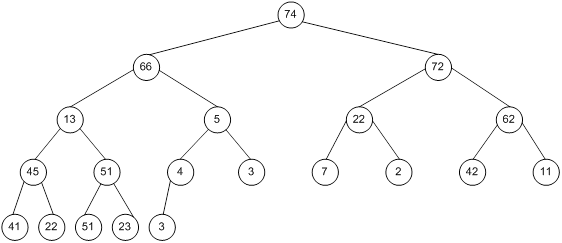
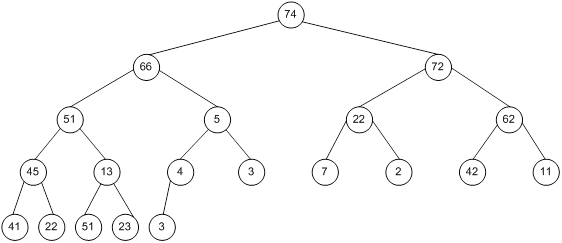
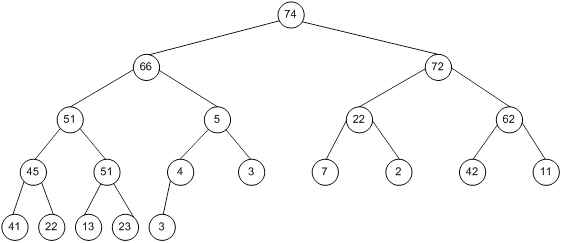
Сортування
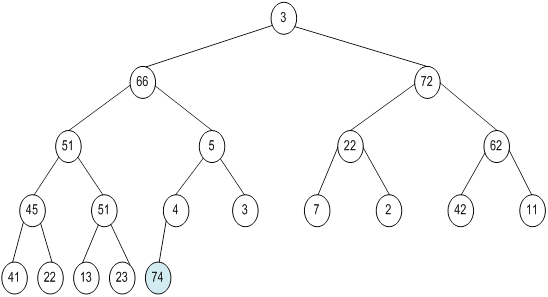
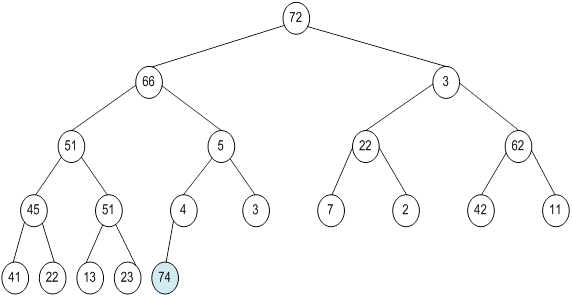
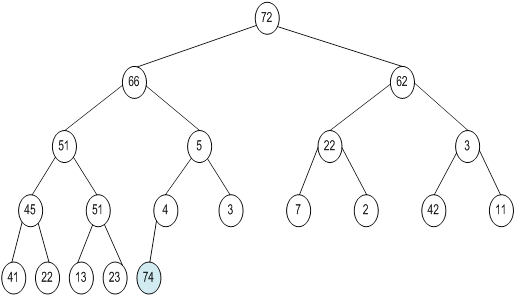
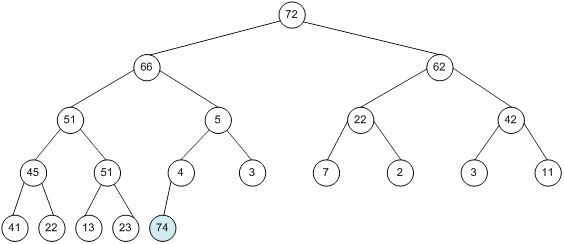
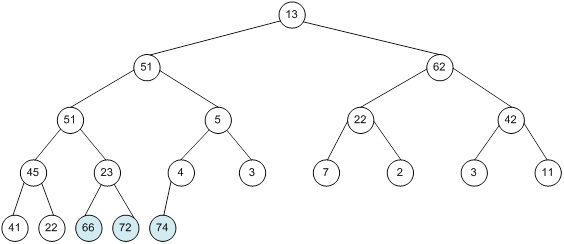
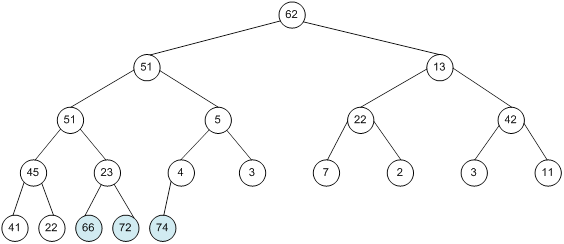
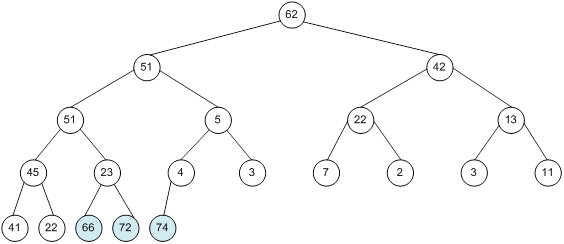
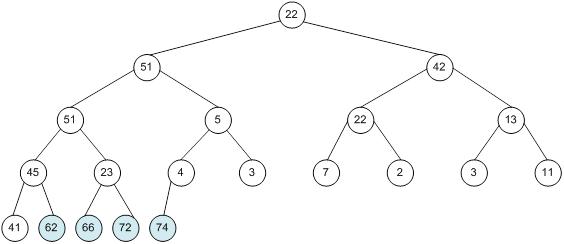
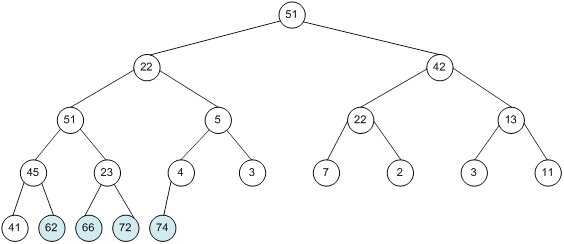
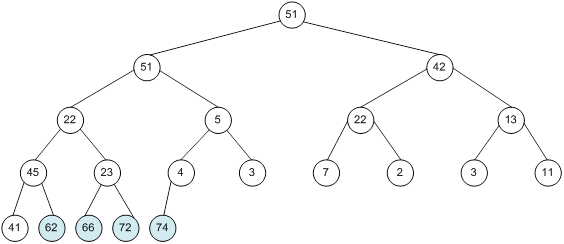
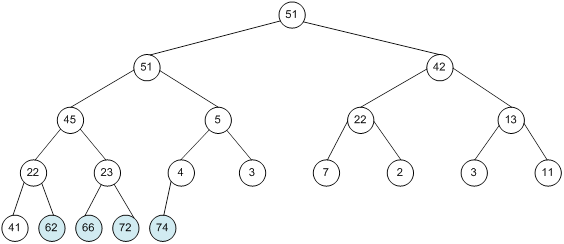
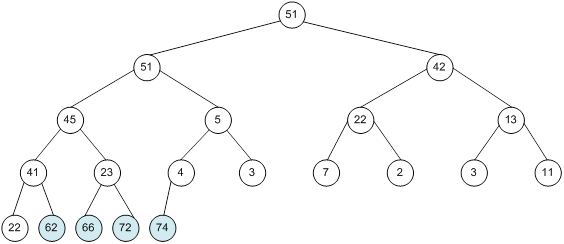

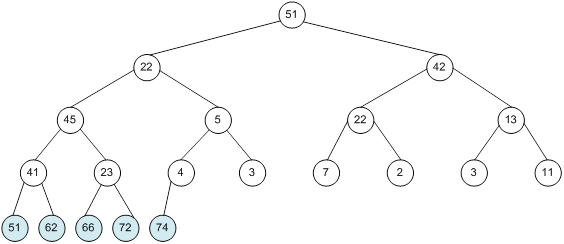
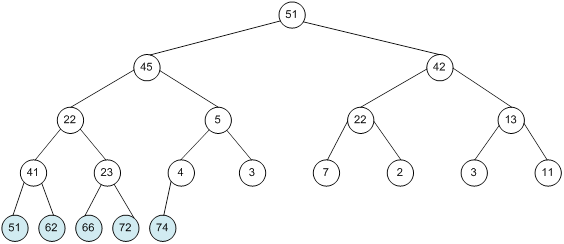
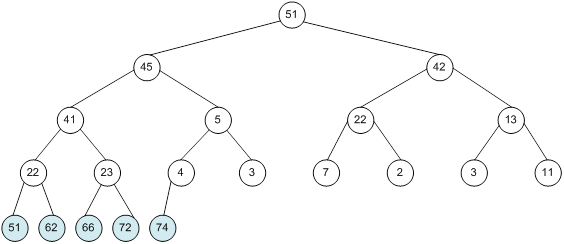
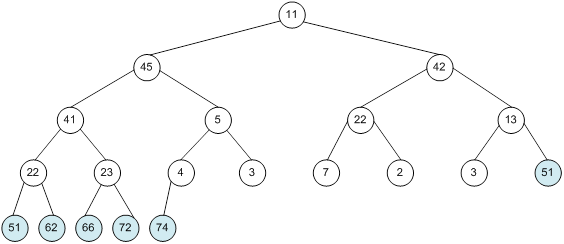
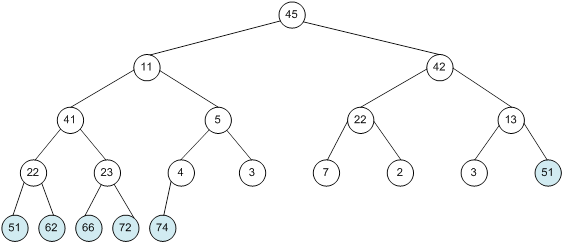
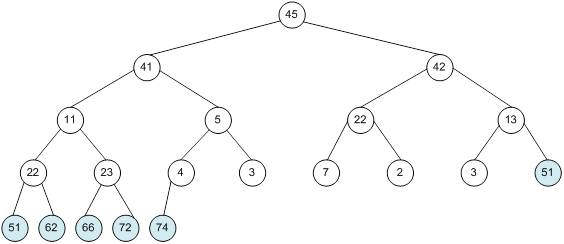
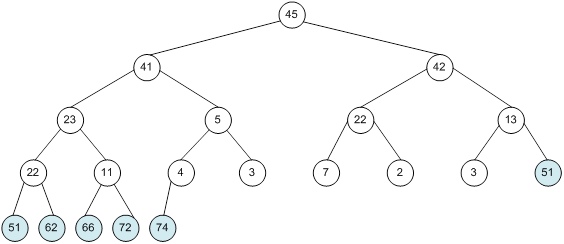
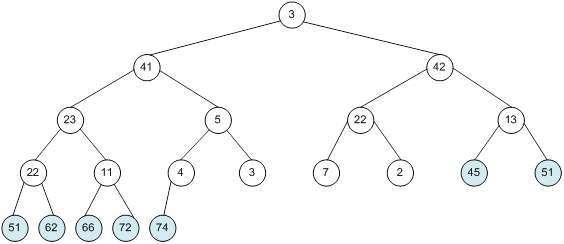
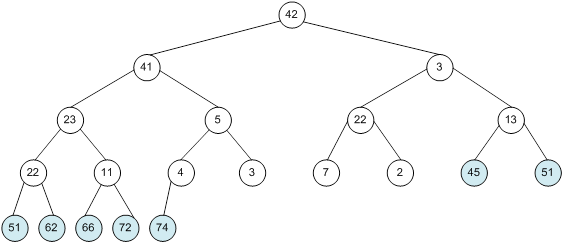
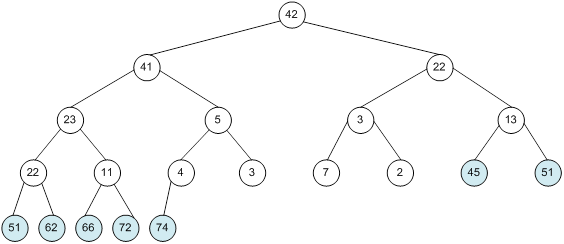
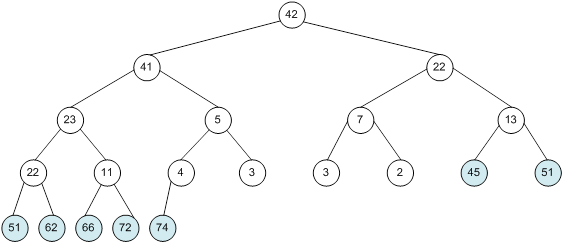
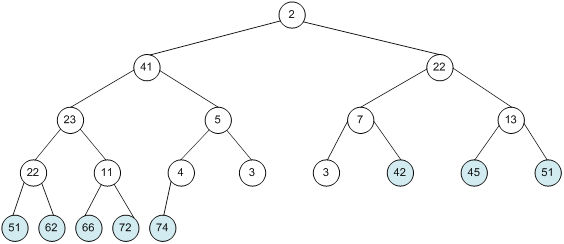
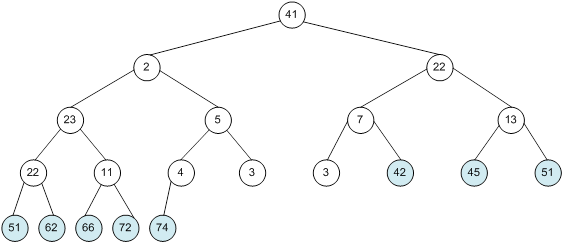
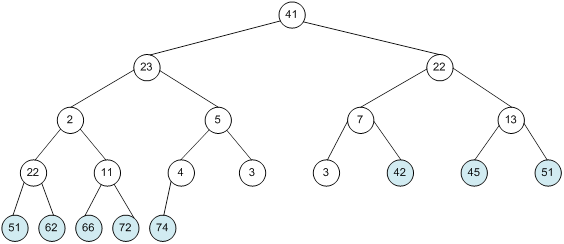
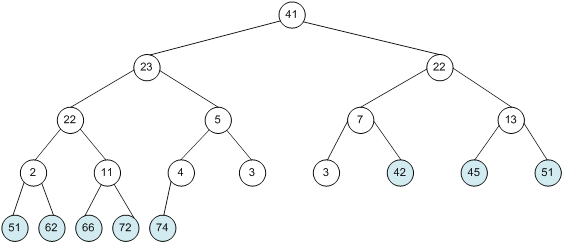
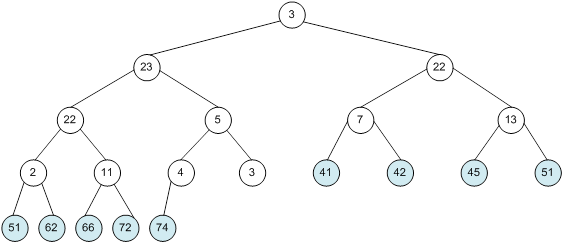
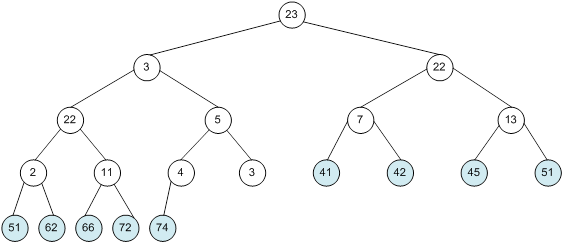
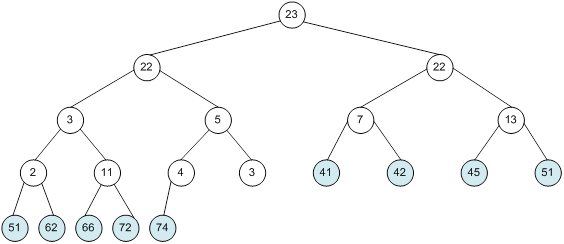
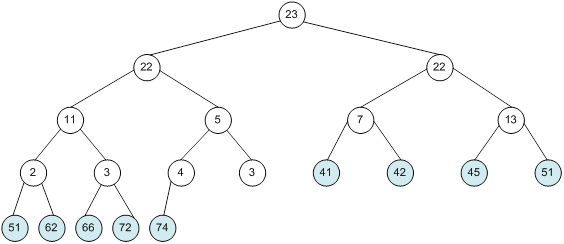
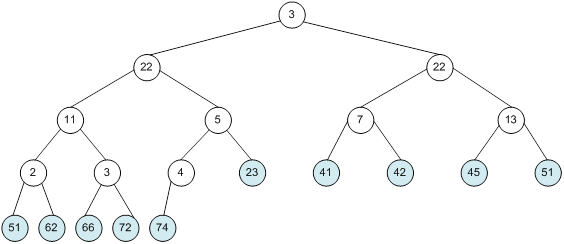
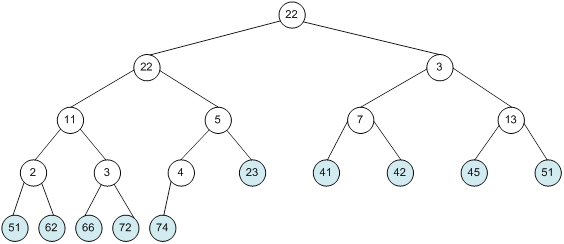
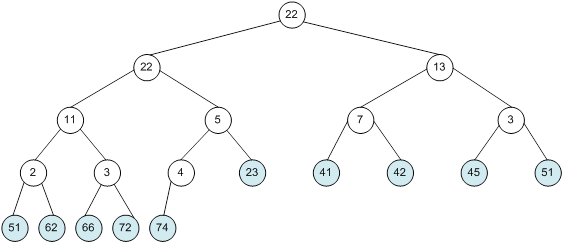
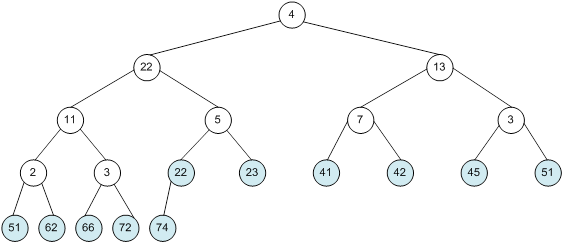
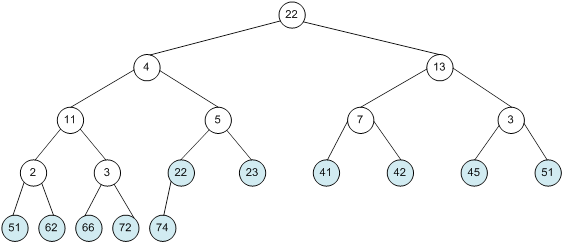
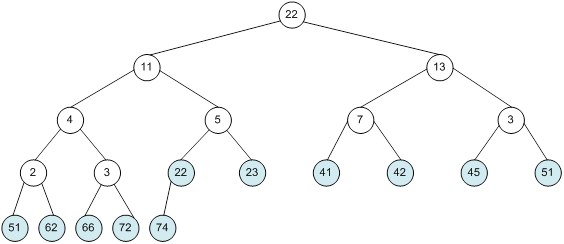
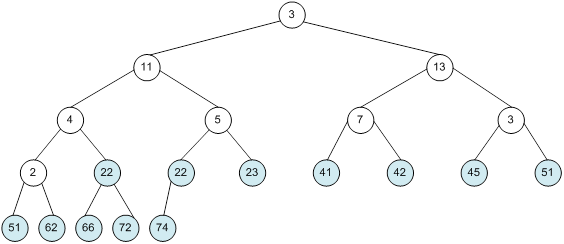
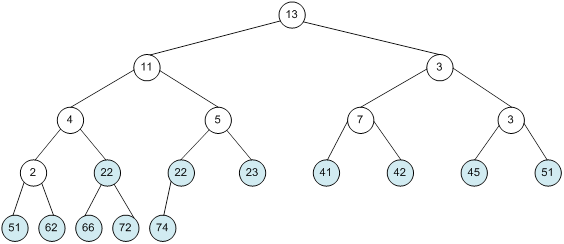
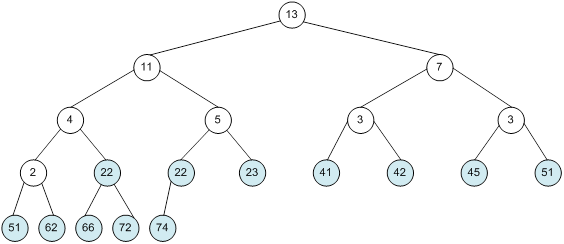
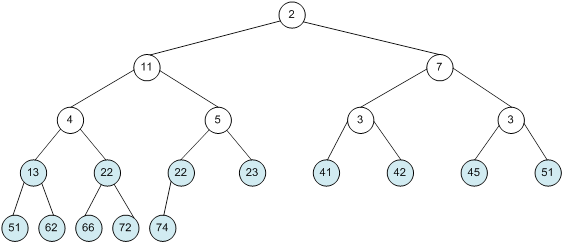
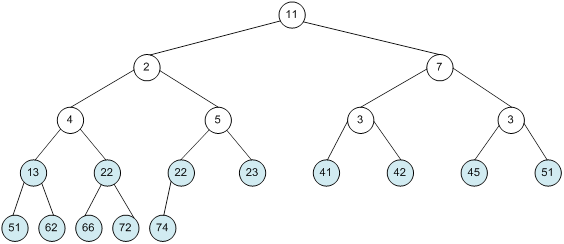
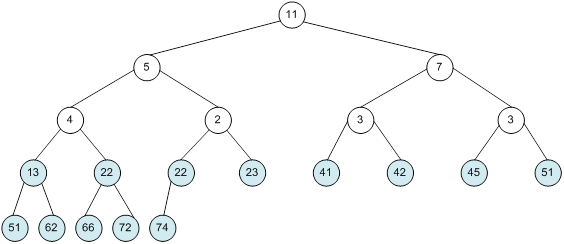
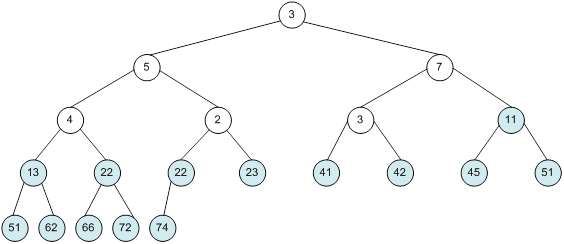
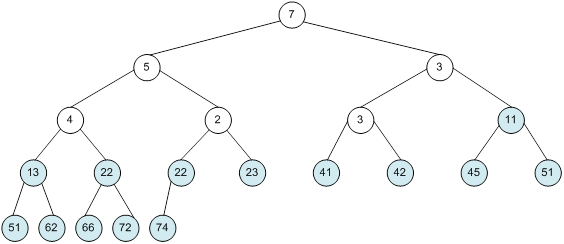
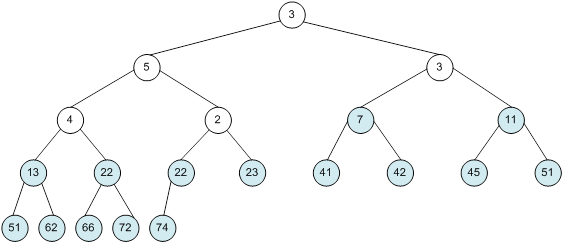
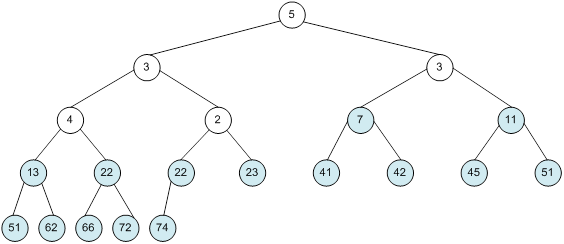
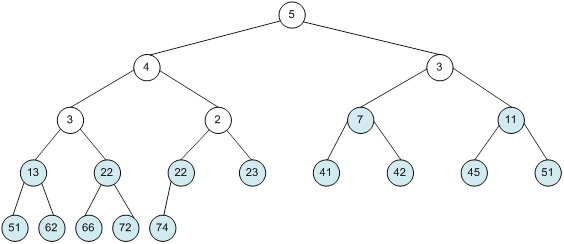
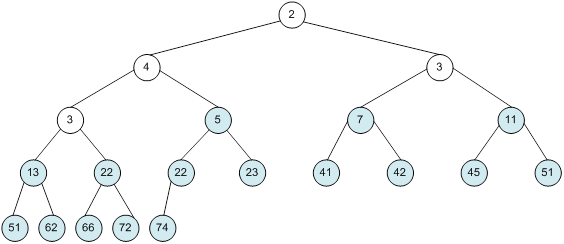
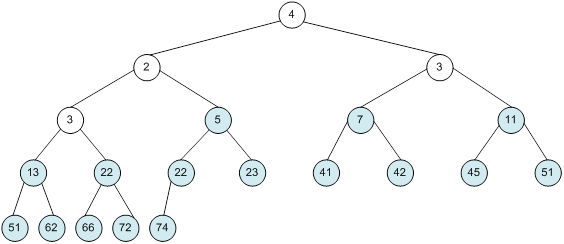

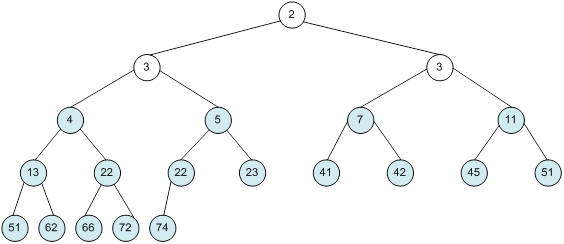
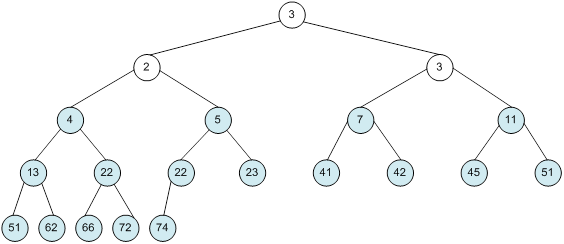
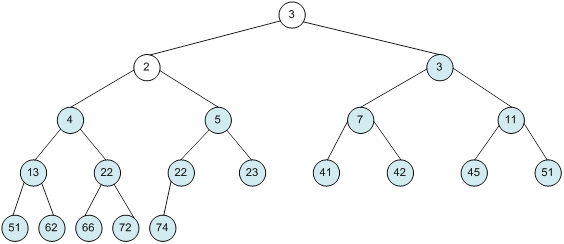
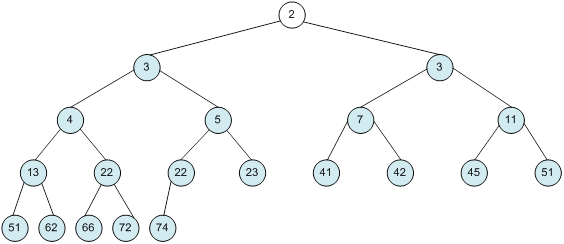
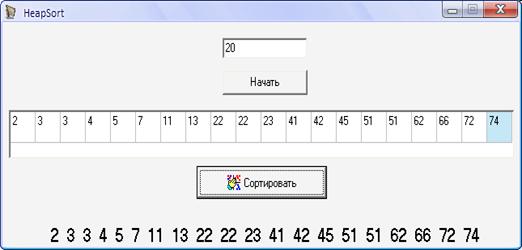
алгоритм програма елемент вікно
Опис використаних в реалізації методу процедур та функцій
Процедура Swap
Procedure Swap(i, j : Integer)
Переставляє місцями елементи масиву A[i] та A[j] за умови , якщо A[i] < A[j].
Процедура Conflict
Procedure Conflict(i, k : Integer)
Вирішує сімейний конфлікт у дереві : якщо найбільший із синів більше, ніж батько, то переставляються батько і цей син (процедура Swap).
Процедура SortTree
Procedure SortTree(i : Integer)
Будує сортуюче дерево за правилами :
1. A[1] - корінь дерева ;
2. Якщо A[i] - вузол дерева і 2i , то A[2*i] - вузол - “лівий син” вузла A[i]
3. Якщо A[i] - вузол дерева і 2i + 1 , то A[2*i+1] - вузол - “правий син” вузла A[i]
Правила 1-3 визначають у масиві структуру дерева, причому глибина дерева не перевершує [log2 n] + 1. Вони ж задають спосіб руху по дереву від кореня до листків. Рух вгору задається правилом 4:
4. Якщо A[i] - вузол дерева та i > 1, то A[i mod 2] - вузол - “батько” вузла A[i].
Процедура Show_result
Procedure Show_result
Виводить в циклі елементи відсортованого масиву на екран.
Процедура get_data
Procedure get_data
Зчитує значення елементів масиву для сортування.
Користувацьке вікно ( форма )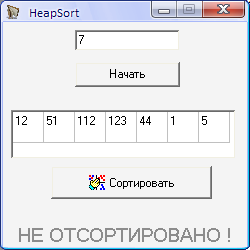
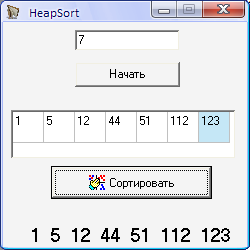
Текст програми
var
Form1: TForm1;
A:array[1..20] of real;
N,k:integer;
implementation
Procedure Swap(i, j : Integer);
Var b : Real;
Begin
If a[i] < a[j] then
begin
b := a[i];
a[i] := a[j];
a[j] := b
end
End;
Procedure Conflict(i, k : Integer);
Var j : Integer;
Begin
j := 2*i;
If j = k then
Swap(i, j)
else
if j < k then
begin
if a[j+1] > a[j] then
j := j + 1;
Swap(i, j);
Conflict(j, k)
End End;
Procedure SortTree(i : Integer);
begin
If i <= n div 2 then
begin
SortTree(2*i);
SortTree(2*i+1);
Conflict(i, n)
end
end;
procedure Show_result;
var i:integer;
begin
Form1.label1.Caption:='';
for i:=1 to N do
begin
Form1.Label1.Caption:=Form1.Label1.Caption+' '+floattostr(A[i]);
Form1.stringGrid1.Cells[i-1,0]:=floattostr(A[i]);
end; end;
procedure get_data;
var i:integer;
begin
for i:=1 to N do
begin
if Form1.StringGrid1.Cells[i-1,0]<>'' then
try
A[i]:=strtoint(Form1.StringGrid1.Cells[i-1,0])
except on EConvertError do showmessage('Недопустимый формат данных ! Присвоено значение "0"'); end
else
showmessage('Обнаружено пустое поле ! Присвоено значение "0"');
end;
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
var i:integer;
begin
get_data;
Label1.Caption:='';
Label1.Enabled:=true;
SortTree(1);
For k := n downto 2 do
begin
Swap(k, 1);
Conflict(1, k - 1) end;
show_result; end;
procedure TForm1.Button1Click(Sender: TObject);
begin
try
N:=strtoint(edit1.Text);
except on EConvertError do
edit1.Clear end;
Form1.Height:=250;
label1.visible:=true;
stringGrid1.Visible:=true;
bitbtn1.Visible:=true;
stringGrid1.ColCount:=n;
stringGrid1.RowCount:=1;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
Form1.Height:=120; end; end