Контрольная работа: Техника и технология кондиционирования воздуха в помещении
МИНОБРНАУКИ РОССИИ
ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СЕРВИСА И ЭКОНОМИКИ»
КИРОВСКИЙ ФИЛИАЛ
КОНТРОЛЬНАЯ РАБОТА
Тема: Техника и технология кондиционирования воздуха в помещении.
Дисциплина: техника и технология
Студент: Криницына Н.М.
Специальность: 080507 (5,5 лет)
Отделение: заочное курс: 2
Преподаватель: Антоненко О.О.
г. Киров 2011г.
Задача 1
коэффициент асимметрия индекс экономика
Приводятся данные по территориям Северо-Западного округа за 2002 год.
| № | Регионы |
Численность населения на 1.01.2000, млн. чел. |
Валовой региональный продукт, млрд. руб. |
Среднемесячная зарплата работающего в экономике, тыс.руб. |
Численность (среднегодовая) занятых в экономике |
Основные фонды в экономике (на конец года), млрд. руб. |
|
| всего, тыс. чел. | в % от численности населения | ||||||
| 1 | Карелия | 0,8 | 11,3 | 1,8 | 312 | 40,8 | 81,3 |
| 2 | Коми | 1,1 | 28,4 | 2,4 | 495 | 43,5 | 179,6 |
| 3 | Архангельская | 1,5 | 22,8 | 1,8 | 567 | 38,9 | 170,5 |
| 4 | Вологодская | 1,3 | 24,1 | 1,7 | 572 | 43,4 | 123,7 |
| 5 | Мурманская | 1,0 | 23,8 | 2,7 | 423 | 42,3 | 142,1 |
| 6 | СПб | 4,7 | 89,8 | 1,9 | 2330 | 50,0 | 425,3 |
| 7 | Ленинградская | 1,7 | 21,2 | 1,5 | 671 | 40,3 | 185,3 |
| 8 | Новгородская | 0,7 | 9,4 | 1,3 | 303 | 41,7 | 61,1 |
| 9 | Псковская | 0,8 | 6,5 | 1,0 | 302 | 37,7 | 69,1 |
Задание:
Необходимо сгруппировать территории со среднемесячной заработной платой работающего в экономике: «до 1,600 тыс. руб.»; «1,600 тыс. руб. и более». В каждой группе рассчитать:
- число территорий;
- долю занятых;
- фондовооруженность.
Оформить в виде таблицы с соблюдением правил.
Проанализировать полученные результаты.
Решение:
Проранжируем группировочный признак - среднемесячная зарплата работающего в экономике, тыс. руб. в прядке возрастания.
Таблица 1 - Ранжированный ряд распределение территорий Северо-Западного округа.
| Номер по ранжиру | Номер округа | Среднемесячная зарплата работающего в экономике, тыс. руб. |
| 1 | 9 | 1,0 |
| 2 | 8 | 1,3 |
| 3 | 7 | 1,5 |
| 4 | 4 | 1,7 |
| 5 | 1 | 1,8 |
| 6 | 3 | 1,8 |
| 7 | 6 | 1,9 |
| 8 | 2 | 2,4 |
| 9 | 5 | 2,7 |
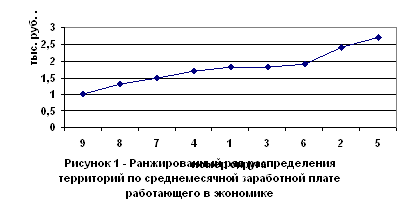
Образуем две группы со среднемесячной зарплатой работающего в экономике, «до 1,600 тыс. руб.» и «1,600 тыс. руб. и более».
Таблица 2 - Расчетная таблица группировки территорий Северо-Западного округа по среднемесячной заработной плате работающего в экономике.
| № группы | Среднемесячная зарплата работающего в экономике, тыс. руб. | Регионы |
Численность населения на 1.01.2000, млн. чел. |
Численность (среднегодовая) занятых в экономике, тыс. чел. |
Основные фонды в экономике (на конец года), млрд. руб. |
| 1 | до 1,600 | Псковская | 0,8 | 302 | 69,1 |
| Новгородская | 0,7 | 303 | 61,1 | ||
| Ленинградская | 1,7 | 671 | 185,3 | ||
|
Итого по 1 группе |
- |
3,2 |
1276 |
315,5 |
|
| 2 | 1,600 и более | Вологодская | 1,3 | 572 | 123,7 |
| Карелия | 0,8 | 312 | 81,3 | ||
| Архангельская | 1,5 | 567 | 170,5 | ||
| СПб | 4,7 | 2330 | 425,3 | ||
| Коми | 1,1 | 312 | 81,3 | ||
| Мурманская | 1,0 | 423 | 142,1 | ||
|
Итого по 2 группе |
- |
10,4 |
4699 |
1122,5 |
|
|
Итого по совокупности |
- |
13,6 |
5975 |
1438 |
Определим число территорий попавших в каждую из групп, а также долю занятых в экономике в общей численности населения как отношение численности занятых в экономике к общей численности населения и выразим в процентах. Показатель фондовооруженности – как отношение основных фондов в экономике к численности занятых в экономике. Результаты представим в таблице.
Таблица 3 - Группировка территорий Северо-Западного округа по среднемесячной заработной плате работающего в экономике.
| Группы регионов по среднемесячной зарплате работающих в экономике | Число регионов | Численность населения, млн. чел. | Основные фонды в экономике, млрд. руб. | Доля занятых в экономике. | Фондовооруженность | |
| Всего | На 1 регион | |||||
| А | 1 | 2 | 3 | 4 | 5=3/2 | 6=5/1 |
| до 1,600 тыс. руб. | 3 | 3,2 | 315,5 | 39,9 | 98,6 | 32,9 |
| 1,600 тыс. руб. и более | 6 | 10,4 | 1122,5 | 43,2 | 107,9 | 18,0 |
| Итого | 9 | 13,6 | 1438 | 41,5 | 103,3 | 25,4 |
В результате проведённого анализа, можно сделать вывод, что в Северо-Западном округе преобладают территории со среднемесячной заработной платой свыше 1600 тыс. руб. их шесть, а до 1600 тыс. руб. всего три. Данная группа при этом имеет большую долю (в расчёте на 1 регион) занятых в экономике и значительно меньшую фондовооружённость – 18 млн. руб./чел. против 32,9 млн. руб./чел. В регионах со средней заработной платой работников, занятых в экономике до 1600 руб. Наибольшая доля занятых в экономике от общей численности населения – 43,2% наблюдается во второй группе со среднемесячной заработной платой от 1600 тыс. руб. и более, однако показатель фондовооружённости здесь ниже, чем впервой группе и в среднем по совокупности. Наибольший уровень фондовооружённости отмечается в группе территорий со среднемесячной зарплатой работающего в экономике до 1600 тыс. руб. и составляет 247,3 тыс. руб. в расчете на одного человека занятого в экономике.
Задача 2
Приводятся сведения по регионам европейской части России
| Регионы | Численность занятых в экономике | Среднемесячный душевой доход населения, руб. | Стоимость валового регионального продукта в среднем на | ||
| всего, млн. чел. | в % от численности населения | 1-го занятого в экономике, тыс. руб. | 1 руб. стоимости основных фондов в экономике, коп. | ||
| Центральный | 13,3 | 45,5 | 2547 | 46,4 | 20,9 |
| Поволжский | 7,0 | 41,9 | 1183 | 34,2 | 15,1 |
Задание
Выполните расчет средних значений каждого показателя, укажите вид и форму использованных средних, приведите расчетные формулы, проверьте правильность результатов.
Решение:
Расчет средней численности занятых в экономике проводим по средней арифметической простой
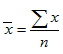
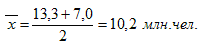
![]()
Средний процент численности занятых в экономике от общей численности населения определим по средней гармонической взвешенной, так как неизвестен показатель, находящийся в знаменателе данного отношения – общая численность населения.
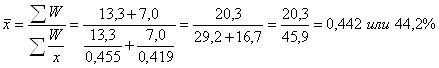 .
.
Средний показатель среднемесячного душевого дохода населения определяется как отношение общего валового дохода населения к численности населения. Неизвестным является числитель – валовой доход населения, которой представляет собой произведение среднемесячного душевого дохода населения на численность населения, таким образом, численность населения выступает частотой, следовательно, применяем формулу средней арифметической взвешенной.
![]()
Средняя стоимость валового регионального продукта в среднем на 1-го занятого в экономике определяется как отношение стоимости валового регионального продукта к численности населения занятого в экономике. Неизвестен числитель, расчет ведем по средней арифметической взвешенной, весом выступает численность населения занятого в экономике.
![]()
Расчет показателя средней стоимости валового регионального продукта в среднем на 1 руб. стоимости основных фондов в экономике проводим по средней гармонической взвешенной, так как неизвестен показатель стоимости основных фондов в экономике, находящийся в знаменателе. Весом выступает численность населения занятого в экономике.
![]() ;
;
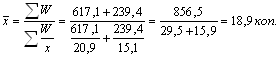
Задача 3
Приводятся данные за 2002 год о распределении территорий РФ по стоимости валового регионального продукта в среднем на 1-го работника, занятого в экономике, тыс. руб.
Группы территорий РФ по стоимости валового регионального продукта в среднем на 1-го работника, занятого в экономике, тыс. руб. |
Число территорий в каждой группе |
| От 12,5 до 22,4 | 16 |
| От 22,4 до 32,3 | 31 |
| От 32,3 до 42,3 | 14 |
| От 42,3до 62,1 | 8 |
| От 62,1 и более | 7 |
| Итого: | 76 |
Задание:
Выполните расчет абсолютных и относительных показателей вариации, коэффициент асимметрии и показатель моды, постройте на одном графике гистограмму и полигон распределения частот, выполните анализ полученных результатов.
Решение:
Составим расчетную таблицу:
Таблица 4 - Расчетная таблица для определения абсолютных и относительных показателей вариации.
| Валовой региональный продукт в среднем на 1-го работника, занятого в экономике, тыс. руб. |
Число территорий
|
Расчетные величины | ||||
|
середина интервала
|
|
|
|
|
||
| От 12,5 до 22,4 | 16 | 17,45 | 279,20 | -16,38 | 262,08 | 4292,87 |
| От 22,4 до 32,3 | 31 | 27,35 | 847,85 | -6,48 | 200,88 | 1301,70 |
| От 32,3 до 42,3 | 14 | 37,30 | 522,20 | 3,47 | 48,58 | 168,57 |
| От 42,3 до 62,1 | 8 | 52,20 | 417,60 | 18,37 | 146,96 | 2699,66 |
| От 62,1 до 81,9 | 7 | 72,00 | 504,00 | 38,17 | 267,19 | 10198,64 |
| Итого: | 76 | - | 2570,85 | - | 925,69 | 18661,44 |
Средний показатель валового регионального продукта в среднем на 1-го работника, занятого в экономике определим по формуле средней арифметической взвешенной
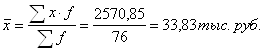
Абсолютные показатели вариации:
1. Размах вариации
![]()
2. Среднее линейное отклонение
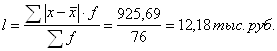
3. Дисперсия
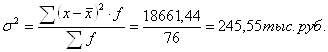
4. Среднее квадратическое отклонение
![]()
Относительные показатели вариации:
1. Коэффициент осцилляции
![]() .
.
2. Линейный коэффициент вариации
![]() .
.
3. Коэффициент вариации
![]() ,
,
так как коэффициент вариации больше 33%, следовательно, совокупность является неоднородной, а средняя величина считается неустойчивой характеристикой совокупности.
Модой называется наиболее часто встречающаяся величина признака.
В интервальном вариационном ряду распределения мода рассчитывается по формуле:
 , где
, где
![]() - нижняя граница модального
интервала;
- нижняя граница модального
интервала;
![]() - размер модального интервала;
- размер модального интервала;
![]() - частота модального интервала;
- частота модального интервала;
![]() - частота интервала предшествующего
модальному;
- частота интервала предшествующего
модальному;
![]() - частота интервала следующего за
модальным.
- частота интервала следующего за
модальным.
Модальным называется интервал, имеющий наибольшую частоту, в нашем случае это интервал от 22,4 до 32,3 тыс. руб.
![]()
Для определения симметричности совокупности используют коэффициент ассиметрии
![]() ,
,
так как коэффициент ассиметрии положительный, следовательно наблюдается правосторонняя ассиметрия.
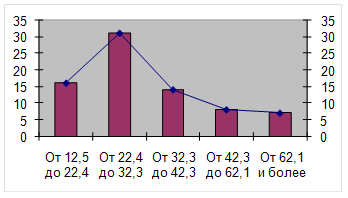
На представленной гистограмме и полигоне распределения отчетливо видно, что наибольшее количество регионов имеют на 1-го работника, занятого в экономике ВВП от 22,4 до 32,3 тыс. руб. Показатели вариации показывают достаточно большие отклонения от среднего значения. Имеется левосторонняя асимметрия.
Задача 4
Структура расходов домашних хозяйств (семей) на конечное потребление в 2002 году в федеральных округах Российской Федерации (в процентах от общего объема расходов на потребление).
| № | Расходы домашних хозяйств (семей) | Федеральные округа | |
| Северо-Западный | Сибирский | ||
| 1 | на покупку продуктов питания | 50,0 | 39,4 |
| 2 | стоимость натуральных поступлений продуктов питания | 5,0 | 14,4 |
| 3 | на покупку непродовольственных товаров | 27,4 | 30,4 |
| 4 | на покупку алкогольных напитков | 2,7 | 2,3 |
| 5 | на оплату услуг | 12,3 | 11,9 |
| 6 | стоимость предоставленных в натуральном выражении дотаций и льгот | 2,5 | 1,6 |
| Итого | 100,0 | 100,0 |
Задание:
Проанализируйте особенности структур, используя оценочные показатели различий структуры.
Решение:
| Федеральные округа | Абсолютная разница | Относительное соотношение | |||
| № | Расходы домашних хозяйств (семей) | Северо-Западный | Сибирский | ||
| 1 | на покупку продуктов питания | 50,0 | 39,4 | 10,6 | 1,27 |
| 2 | стоимость натуральных поступлений продуктов питания | 5,0 | 14,4 | -9,4 | 0,35 |
| 3 | на покупку непродовольственных товаров | 27,4 | 30,4 | -3 | 0,90 |
| 4 | на покупку алкогольных напитков | 12,7 | 2,3 | 10,4 | 5,52 |
| 5 | на оплату услуг | 12,3 | 11,9 | 0,4 | 1,03 |
| 6 | стоимость предоставленных в натуральном выражении дотаций и льгот | 2,5 | 1,6 | 0,9 | 1,56 |
| Итого | 100,0 | 100,0 |
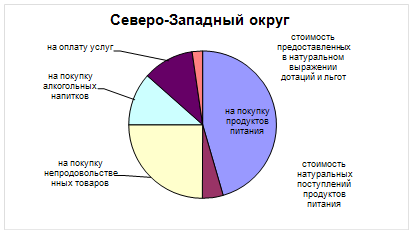
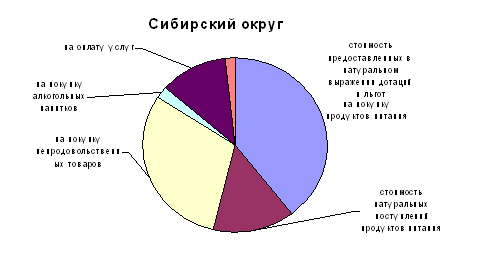
Анализируя структуру расходов домашних хозяйств в Северо-Западном и Сибирском федеральных округах, отметим, что наибольший удельный вес от общего объема расходов на потребление приходится на покупку продуктов питания. В Северо-Западном округе этот удельный вес составляет 50,0%, что выше, чем в Сибирском на 10,6 процентных пункта. При этом доля расходов, приходящихся на покупку непродовольственных товаров в Сибирском федеральном округе больше, чем в Северо-Западном округе на 3 процентных пункта. Значительные различия по округам, наблюдаются в стоимости натуральных поступлений продуктов питания, доля этих поступлений в Сибирском округе достигает 14,4 %, а Северо-Западном – лишь 5,0%, разница составляет 9,4 процентных пункта. Расходы на оплату услуг несколько (0,4 процентных пункта) превышают в Северо-Западном округе, по сравнению с Сибирским федеральным округом. Различия с структуре расходов на покупку алкогольных напитков и стоимости предоставленных в натуральном выражении дотаций и льгот незначительны и составляют от 0,4 до 0,9 процентных пункта, это превышение наблюдается в Северо-Западном округе.
Для обобщенного анализа различий в структуре рассчитаем интегральный коэффициент структурных сдвигов (показатель К. Гатева):
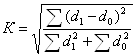 .
.
Измеряется от ![]() , чем ближе коэффициент к
1,тем сильнее изменения в структуре.
, чем ближе коэффициент к
1,тем сильнее изменения в структуре.
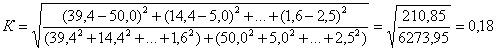 ,
,
следовательно различия в структуре незначительные.
Задача 5
Имеются фактические данные государственной статистики о системе учреждений отдыха.
| Виды учреждений отдыха | Число учреждений | В них отдыхало, тыс. чел. | ||
| 1998 | 2002 | 1998 | 2002 | |
| Дома отдыха и пансионаты | 372 | 394 | 970 | 1435 |
| Базы отдыха | 1542 | 1880 | 1251 | 1934 |
| Туристические базы | 185 | 193 | 520 | 137 |
| Итого: | - | - | 2741 | 3506 |
Задание:
1. Определите недостающий признак-фактор и рассчитайте его отчетные и базисные значения.
2. Рассчитайте общие индексы: а) числа учреждений; б) численности отдыхавших в них; в) индекс недостающего признак-фактора. Представьте результаты в системе взаимосвязанных индексов.
Решение:
1. Рассчитаем недостающий признак-фактор – это число отдохнувших в одном учреждении, как отношение общего числа отдохнувших в учреждениях к числу учреждений и данные расчета представим в таблице за базисный 1998 год (S0) и отчетный 2002 год (S1). Введем обозначения и определим условный показатель необходимый для дальнейшего анализа.
Таблица 5 - Данные государственной статистики о системе учреждений отдыха.
| Виды учреждений отдыха | Число учреждений |
В них отдыхало, тыс. чел. |
Число отдохнувших в одном учреждении, чел. | Условное число отдохнувших в учреждениях отдыха, тыс. чел. | |||
|
У0 |
У1 |
У0S0 |
У1S1 |
S0 |
S1 |
У0S1 |
|
| Дома отдыха и пансионаты | 372 | 394 | 970 | 1435 | 2608 | 3642 | 1355 |
| Базы отдыха | 1542 | 1880 | 1251 | 1934 | 811 | 1029 | 1587 |
| Туристические базы | 185 | 193 | 520 | 137 | 2811 | 710 | 131 |
| Итого: | - | - | 2741 | 3506 | - | - | 3073 |
2. Рассчитаем общие индексы:
а) числа учреждений
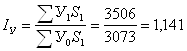 ;
;
б) численности отдыхавших в них
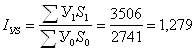 ;
;
в) числа отдохнувших в одном учреждении
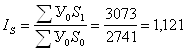 ;
;
Взаимосвязь индексов: ![]() , таким образом общее число
отдохнувших в 2002 году по сравнению с 1998 годом увеличилось на 27,9%, в том
числе за счет увеличения числа учреждений на 14,1% и увеличения числа
отдохнувших в каждом из них на 12,1%.
, таким образом общее число
отдохнувших в 2002 году по сравнению с 1998 годом увеличилось на 27,9%, в том
числе за счет увеличения числа учреждений на 14,1% и увеличения числа
отдохнувших в каждом из них на 12,1%.
Задача 6
Предлагается проанализировать данные о реализации фруктов в магазинах района.
| Группы фруктов | Выручка от реализации товаров, млн. руб. |
Индивидуальные индексы цен |
|
|
база |
отчет |
||
| Бананы | 80 | 85,0 | 0,90 |
| Яблоки | 132 | 149,6 | 1,04 |
| Апельсины | 65 | 72,3 | 1,09 |
| Итого | 277 | 306,9 | - |
Задание:
1. Рассчитайте темпы прироста цен по каждой из трех товарных групп.
2. Рассчитайте общий индекс цен как средний из индивидуальных по схеме: а) Паше; б) Ласпейреса.
3. Объясните причину различий их значений.
Решение:
1. Темпы прироста цен по каждой товарной группе представлены в таблице в виде индивидуальных индексов цен, так по группе бананов наблюдается снижение цен на 10%, а группе яблок увеличение - на 4%, а по апельсинам увеличение цен составило 9%.
2. Индекс цен Пааше
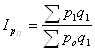 ,
,
так как ![]() , тогда средний
гармонический индекс цен Пааше будет
, тогда средний
гармонический индекс цен Пааше будет
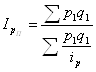 ;
;
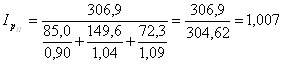 .
.
Общее повышение цен составило 7%.
Индекс цен Ласпейреса
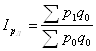 , так как
, так как ![]() , тогда средний
арифметический индекс цен Ласпейресса будет
, тогда средний
арифметический индекс цен Ласпейресса будет
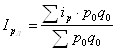 ;
; ![]() .
.
Повышение цен по всем товарным группам составило 11%.
3. При построении индекса цен Пааше объем товарооборота фиксируется на уровне отчетного периода, характеризуя изменение цены в расчете на количество и состав реализованной продукции отчетного периода. А в индексе цен Ласпейресса используются базисные веса, показывая во сколько раз изменились бы потребительские расходы в текущем периоде, по сравнению с базисным, если бы при изменении цен уровень потребления оставался прежним. Поэтому обе системы расчета дают различные результаты, хотя и достаточно близко отражают главные тенденции изменения товарооборота.
Задача 7
Приводятся данные государственной статистики о среднедушевых расходах за месяц, тыс. руб. по территориям Российской Федерации за 2002год.
| № | Территория | Расход | № | Территория | Расход | № | Территория | Расход |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | Белгородская обл. | 1,27 | 27 | Новгородская обл. | 1,52 | 53 | Саратовская обл. | 1,15 |
| 2 | Брянская обл. | 0,95 | 28 | Псковская обл. | 1,09 | 54 | Ульяновская обл. | 1,07 |
| 3 | Владимирская обл. | 0,97 | 29 | Респ. Адыгея | 0,78 | 55 | Курганская обл. | 0,96 |
| 4 | Воронежская обл. | 1,19 | 30 | Респ. Дагестан | 0,48 | 56 | Свердловская обл. | 1,74 |
| 5 | Ивановская обл. | 0,85 | 31 | Респ. Ингушетия | 0,26 | 57 | Тюменская обл. | 3,09 |
| 6 | Калужская обл. | 1,13 | 32 | Кабардино-балкарская респ. | 0,84 | 58 | Челябинская обл. | 1,57 |
| 7 | Костромская обл. | 0,98 | 33 | Респ. Калмыкия | 0,45 | 59 | Респ. Алтай | 0,77 |
| 8 | Курская обл. | 1,11 | 34 | Карачаево-Черкесская респ. | 0.72 | 60 | Респ. Бурятия | 1,18 |
| 9 | Липецкая обл. | 1,46 | 35 | Респ. Северная Осетия-Алания | 1,33 | 61 | Респ. Тыва | 0,57 |
| 10 | Московская обл. | 1,93 | 36 | Краснодарский край | 1,65 | 62 | Респ. Хакасия | 1,37 |
| 11 | г. Москва | 9,96 | 37 | Ставропольский край | 1,47 | 63 | Алтайский край | 1,10 |
| 12 | Орловская обл. | 1,24 | 38 | Астраханская обл. | 1,21 | 64 | Красноярский край | 1,77 |
| 13 | Рязанская обл. | 1,01 | 39 | Волгоградская обл. | 1,04 | 65 | Иркутская обл. | 1,86 |
| 14 | Смоленская обл. | 1,49 | 40 | Ростовская обл. | 1,61 | 66 | Кемеровская обл. | 1,61 |
| 15 | Тамбовская обл. | 1,27 | 41 | Респ. Башкортостан | 1,45 | 67 | Новосибирская обл. | 2,03 |
| 16 | Тверская обл. | 1,08 | 42 | Респ. Марий Эл | 0,70 | 68 | Омская обл. | 1,33 |
| 17 | Тульская обл. | 1,16 | 43 | Респ. Мордовия | 0,89 | 69 | Томская обл. | 1,60 |
| 18 | Ярославская обл. | 1,47 | 44 | Респ. Татарстан | 1,49 | 70 | Читинская обл. | 0,75 |
| 19 | Респ. Карелия | 1,59 | 45 | Удмуртская респ. | 1,22 | 71 | Респ. Саха | 2,48 |
| 20 | Респ. Коми | 1,92 | 46 | Чувашская респ. | 0,94 | 72 | Приморский край | 1,75 |
| 21 | Архангельская обл. | 1,29 | 47 | Кировская обл. | 1,10 | 73 | Хабаровский край | 1,90 |
| 22 | Вологодская обл. | 1,38 | 48 | Нижегородская обл. | 1,39 | 74 | Амурская обл. | 1,40 |
| 23 | Калининградская обл. | 1,78 | 49 | Оренбургская обл. | 1,06 | 75 | Камчатская обл. | 2,66 |
| 24 | Ленинградская обл. | 1,18 | 50 | Пензенская обл. | 0,90 | 76 | Магаданская обл. | 2,22 |
| 25 | г. Санкт-Петербург | 2,66 | 51 | Пермская обл. | 1,80 | 77 | Сахалинская обл. | 1,99 |
| 26 | Мурманская обл. | 2,59 | 52 | Самарская обл. | 2,76 |
Задание:
1. Провести 14%-ую бесповторную выборку, используя таблицу случайных чисел.
2. Рассчитайте выборочную величину среднемесячных душевых расходов и долю территорий, где душевые расходы меньше среднедушевого прожиточного минимума трудоспособного населения за месяц, который составил в 2000 году 1,32 тыс. руб.
3. Определите среднюю возможную ошибку и с вероятностью 0,9643 предельную ошибку для выборочной средней и для выборочной доли.
4. Рассчитайте доверительный интервал, в котором будут находиться генеральная средняя и генеральная доля.
Решение:
1.
Определим число
единиц выборочной совокупности при 14% выборке ![]() единиц.
С помощью таблицы случайных чисел проведем отбор единиц. Воспользуемся первой
строкой таблицы случайных чисел и так как исходные показатели двухзначные, то
ряд выпишем следующим образом: 66, 19, 42, 89, 26, 99, 54, 71, 66, 25, 45, 51,
56, 79, 53... Исключим значения больше 77, а также повторяющиеся, так как
выборка бесповторная, следовательно, ряд будет следующим: 66, 19, 42, 26, 54,
71, 25, 45, 51, 56, 53. Выпишем соответствующие им значения среднедушевых
расходов за месяц, тыс. руб.
единиц.
С помощью таблицы случайных чисел проведем отбор единиц. Воспользуемся первой
строкой таблицы случайных чисел и так как исходные показатели двухзначные, то
ряд выпишем следующим образом: 66, 19, 42, 89, 26, 99, 54, 71, 66, 25, 45, 51,
56, 79, 53... Исключим значения больше 77, а также повторяющиеся, так как
выборка бесповторная, следовательно, ряд будет следующим: 66, 19, 42, 26, 54,
71, 25, 45, 51, 56, 53. Выпишем соответствующие им значения среднедушевых
расходов за месяц, тыс. руб.
| № | Регион | Расход |
| 66 | Кемеровская обл. | 1,61 |
| 19 | Респ. Карелия | 1,59 |
| 42 | Респ. Марий Эл | 0,70 |
| 26 | Мурманская обл. | 2,59 |
| 54 | Ульяновская обл. | 1,07 |
| 71 | Респ. Саха | 2,48 |
| 25 | г. Санкт-Петербург | 2,66 |
| 45 | Удмуртская респ. | 1,22 |
| 51 | Пермская обл. | 1,80 |
| 56 | Свердловская обл. | 1.74 |
| 53 | Саратовская обл. | 1,15 |
2.
Определим
выборочную величину среднемесячных душевых расходов ![]() и долю территорий, где
душевые расходы меньше среднедушевого прожиточного минимума трудоспособного
населения за месяц, который составил в 2000 году 1,32 тыс. руб., следовательно
и долю территорий, где
душевые расходы меньше среднедушевого прожиточного минимума трудоспособного
населения за месяц, который составил в 2000 году 1,32 тыс. руб., следовательно![]() .
.
3. Средняя ошибка при случайном бесповторном отборе для выборочной средней определяется по формуле
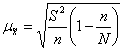 , где
, где
![]() - дисперсия признака в выборочной
совокупности;
- дисперсия признака в выборочной
совокупности;
![]() - объем выборки (число обследованных
единиц);
- объем выборки (число обследованных
единиц);
![]() - объем генеральной совокупности
(число входящих в нее единиц);
- объем генеральной совокупности
(число входящих в нее единиц);
![]()
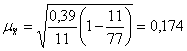 .
.
Средняя ошибка при случайном бесповторном отборе для выборочной доли определяется по формуле
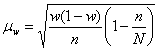 .
.
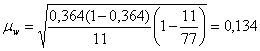 .
.
Предельная ошибка выборки ![]() , где
, где
![]() - нормированное отклонение или
«коэффициент доверия», зависящий от вероятности, с которой гарантируется
предельная ошибка выборки;
- нормированное отклонение или
«коэффициент доверия», зависящий от вероятности, с которой гарантируется
предельная ошибка выборки;
![]() - средняя ошибка выборки.
- средняя ошибка выборки.
Значение ![]() при
уровне вероятности 0,9643 составит 2,1.
при
уровне вероятности 0,9643 составит 2,1.
Предельная ошибка выборки для средней
![]() , а для выборочной доли
, а для выборочной доли ![]() .
.
4.
Доверительный
интервал, в котором будут находиться генеральная средняя ![]() , т.е.
, т.е. ![]() ,тогда
,тогда ![]() , следовательно
, следовательно ![]() и генеральная доля
и генеральная доля ![]() , т.е.
, т.е. ![]() , тогда
, тогда ![]() , следовательно
, следовательно ![]() или
или ![]() . Таким образом с
вероятностью 96,43% можно утверждать, что значение генеральной средней и доли
следует ожидать в этих пределах.
. Таким образом с
вероятностью 96,43% можно утверждать, что значение генеральной средней и доли
следует ожидать в этих пределах.
Задача 8
Предлагается проанализировать фактические данные о производстве тканей в РФ, млн. кв. м.
| Годы | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| Млн. кв. м | 7619 | 5090 | 3739 | 2197 | 1774 | 1431 | 1565 | 1384 | 1666 | 2329 | 2617 |
Задание:
1. Определите вид динамического ряда и постройте график фактических уровней.
2. Рассчитайте показатели динамики за каждый год изучаемого отрезка времени.
3. Выполните расчет динамических средних за I-ый период (1992-1996 гг.) и за II-ой период(1997-2002 гг.).
4. Проанализируйте результаты, сделайте выводы.
Решение:
1. Представленный динамический ряд является интервальным, так как его уровни характеризуют производство тканей в РФ за периоды времени – интервал равен году.
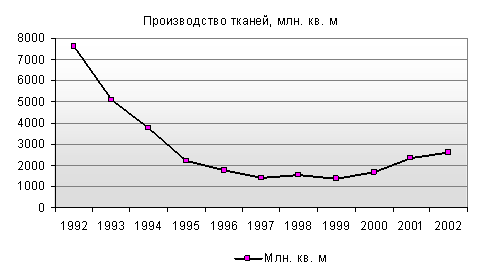
Рассчитаем показатели динамики за каждый год изучаемого отрезка времени:
Показатели динамики рассчитывают «цепным» и «базисным» способом. При базисном способе расчета Уi сравнивают с одним постоянным уровнем, принятым за базу сравнения (обычно с начальным уровнем У0). При цепном способе расчета каждый уровень ряда динамики Уi сравнивают с предыдущим уровнем ряда Уi-1, таким образом, мы получаем показатели с переменной базой сравнения.
Абсолютный прирост – разность двух уровней рядов динамики. Показывает на сколько данный уровень больше или меньше предыдущего или базисного.
![]() ;
; ![]() .
.
Темп роста – это отношение одного уровня рядов динамики к другому, принятому за базу сравнения (выражается в %).
![]() ;
; ![]() .
.
Темп прироста – отношение абсолютного прироста к уровню, принятому за базу сравнения. Характеризует абсолютный прирост в относительных величинах.
![]() ;
; ![]() .
.
Абсолютное значение 1% прироста определяется как отношение абсолютного прироста к темпу прироста, выраженному в %.
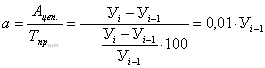 .
.
Расчеты представим в таблице:
Таблица 6 - Производство тканей в Российской Федерации.
| Годы | Производство тканей в РФ, млн. кв. м. | Обозначение уровня | Абсолютный прирост, млн. кв. м | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, млн. кв.м. | |||
| базисный | цепной | Базисный | Цепной | Базисный | Цепной | ||||
| 1992 | 7619 |
У0 |
- | - | 100,0 | - | 0 | - | - |
| 1993 | 5090 |
У1 |
-2529 | -2529 | 66,8 | 66,8 | -33,2 | -33,2 | 76,19 |
| 1994 | 3739 |
У2 |
-3880 | -1351 | 49,1 | 73,5 | -50,9 | -26,5 | 50,90 |
| 1995 | 2197 |
У3 |
-5422 | -1542 | 28,8 | 58,8 | -71,2 | -41,2 | 37,39 |
| 1996 | 1774 |
У4 |
-5845 | -423 | 23,8 | 80,7 | -76,2 | -19,3 | 21,97 |
| 1997 | 1431 |
У5 |
-6188 | -343 | 18,8 | 80,7 | -81,2 | -19,3 | 17,74 |
| 1998 | 1565 |
У6 |
-6054 | 134 | 20,5 | 109,4 | -79,5 | 9,4 | 14,31 |
| 1999 | 1384 |
У7 |
-6235 | -181 | 18,2 | 88,4 | -81,8 | -11,6 | 15,65 |
| 2000 | 1666 |
У8 |
-5953 | 282 | 21,9 | 120,4 | -78,1 | 20,4 | 13,84 |
| 2001 | 2329 |
У9 |
-5290 | 663 | 30,6 | 139,8 | -69,4 | 39,8 | 16,66 |
| 2002 | 2617 |
У10 |
-5002 | 288 | 34,3 | 112,4 | -65,7 | 12,4 | 23,29 |
3. Проведем расчет динамических средних за I-ый период (1992-1996 гг.) и за II-ой период (1997-2002 гг.).
Средний уровень
![]() ;
;
В I-ом периоде ![]()
Во II-ом периоде ![]()
Средний абсолютный прирост
![]() ,
,
где ![]() -
конечный уровень ряда динамики,
-
конечный уровень ряда динамики, ![]() -
начальный уровень,
-
начальный уровень, ![]() - число уровней
не считая начального.
- число уровней
не считая начального.
В I-ом периоде ![]()
Во II-ом периоде ![]()
Средний темп роста 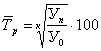 ;
;
В I-ом периоде ![]() 69,5%.
69,5%.
Во II-ом периоде ![]() 112,8%.
112,8%.
Средний темп прироста ![]() ;
;
В I-ом периоде ![]() = 69,5 –
100 = - 30,5%.
= 69,5 –
100 = - 30,5%.
Во II-ом периоде ![]() = 112,8
– 100 = 12,8%.
= 112,8
– 100 = 12,8%.
Таким образом, среднегодовые показатели ряда динамики в I-ом периоде (1992-1996 гг.) характеризуют тенденцию снижения объемов производства тканей в РФ в среднем ежегодно на 1461,25 млн.кв.м. или на 30,5% при среднегодовом объеме производства 4083,8 млн. кв.м., а во II-ом периоде (1997-2002 гг.) наблюдается тенденция увеличения ежегодно на 237,2 млн.кв.м. или на 12,8% при среднегодовом объеме производства 1832 млн. кв.м.ткан.