Контрольная работа: Розробка одноконтурної автоматичної системи регулювання (АСР)
ЗМІСТ
Вступ
1. Теоретична частина
2. Практична частина
Висновок
Література
Вступ
Тема контрольної роботи «Розробка одноконтурної автоматичної системи регулювання (АСР)» З дисципліни «Основи автоматики й автоматизації».
Проблема забезпечення необхідних властивостей лінійних автоматичних систем дуже складна. У ній можуть бути виділені насамперед наступні локальні задачі:
- забезпечення стійкості системи (стабілізація);
- підвищення запасу стійкості системи (демпфірування);
- підвищення точності регулювання в сталих режимах (зменшення або усунення статичної помилки відтворення завдання, зменшення або усунення впливу постійних збурюючих впливів);
- поліпшення перехідних процесів (збільшення швидкодії, максимальне зменшення динамічних помилок відтворення завдання і впливу збурень).
Якість регулювання системи в першу чергу визначається параметрами настроювання регуляторів. Однак у ряді випадків забезпечення стійкості системи або необхідного запасу стійкості не представляється можливим досягти тільки зміною цих параметрів.
Це зв'язано з тим, що необхідні значення настроювальних параметрів неможливо практично реалізувати при даній структурі системи.
З точки зору вимог до точності АСР в сталих режимах корекція динамічних властивостей АСР може знадобитися для збільшення порядку астатизму або коефіцієнта передачі системи при збереженні стійкості та визначеної якості перехідних процесів.
У цьому випадку необхідно застосовувати спеціальні пристрої, що корегують динамічні властивості системи таким чином, щоб забезпечувалася необхідна якість її функціонування. Існують різні методи підключення коригувальних пристроїв у систему регулювання. Розглянемо найбільш поширені з них [7].
1.Теоретична частина
лінійна автоматична система корегування
Послідовний коригувальний пристрій – підключають безпосередньо після датчика неузгодженості або після попереднього підсилювача (рис. 1).
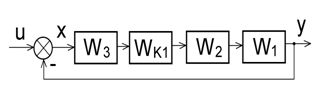
Рис. 1. Послідовне підключення коригувального пристрою
Передаточна
функція коригувального пристрою позначена як ![]() .
Підключення коригувального пристрою після попереднього підсилюваач застосовується
частіше. Справа в тому, що рівень сигналу неузгодженості звичайно дуже малий і
коригувальний пристрій знижує його ще більше. Тому при першому варіанті
включення послідовного коригувального пристрою треба мати попередній підсилювач
значно більшої чутливості, ніж при другому варіанті.
.
Підключення коригувального пристрою після попереднього підсилюваач застосовується
частіше. Справа в тому, що рівень сигналу неузгодженості звичайно дуже малий і
коригувальний пристрій знижує його ще більше. Тому при першому варіанті
включення послідовного коригувального пристрою треба мати попередній підсилювач
значно більшої чутливості, ніж при другому варіанті.
Паралельно–зустрічний коригувальний пристрій – його підключення показано на рис. 2.
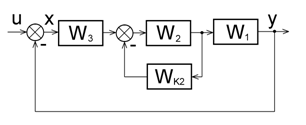
Рис. 2. Паралельно–зустрічне підключення коригувального пристрою
В даному випадку
коригувальний пристрій є зворотним зв’язком, як правило від’ємним, якій охоплює
один з елементів прямого ланцюга системи. Звичайно цей елемент є або виконавчим
елементом, або вихідним каскадом підсилювача (підсилювач потужності). Його
передаточну функцію позначимо ![]() .
.
Передаточна функція ділянки ланцюгу з паралельно–зустрічним коригувальним пристроєм:
 .
.
Звичайно в достатньо широкому й істотному для якості системи діапазоні частот справедливо нерівність:
![]() . (1)
. (1)
Тоді для цього діапазону частот справедливо:
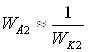 . (2)
. (2)
Таким чином, при задоволенні нерівності (1) властивості ділянки ланцюга з паралельно–зустрічним коригувальним пристроєм визначаються тільки лише властивостями цього коригувального пристрою.
Зазначена
обставина є великою перевагою паралельно-зустрічного коригувального пристрою.
При задоволенні нерівності (1) властивості ділянки ![]() прямого
ланцюга, охопленого паралельно-зустрічним коригувальним пристроєм, і їхні зміни
в процесі дії системи не впливають на властивості системи. Несуттєві
нелінійності цієї ділянки і зміни його параметрів (коефіцієнтів передатної
функції
прямого
ланцюга, охопленого паралельно-зустрічним коригувальним пристроєм, і їхні зміни
в процесі дії системи не впливають на властивості системи. Несуттєві
нелінійності цієї ділянки і зміни його параметрів (коефіцієнтів передатної
функції ![]() ) не позначаються на
динамічних властивостях системи. Це справедливо тільки при незмінних параметрах
самого паралельно-зустрічного пристрою.
) не позначаються на
динамічних властивостях системи. Це справедливо тільки при незмінних параметрах
самого паралельно-зустрічного пристрою.
Достоїнства даного коригувального пристрою також у тім, що його вхід підключений до виходу виконавчого елемента чи підсилювача потужності, тобто до виходу потужного елемента з високим рівнем сигналу. Тому в якості паралельно-зустрічних коригувальних пристроїв можуть бути використані навіть досить потужні елементи.
Варто помітити,
що вплив місцевих зворотних зв'язків, що реалізують паралельно-зустрічні
коригувальні пристрої, дуже різноманітно. Коригувальні зворотні зв'язки
поділяються на жорсткі і гнучкі. Жорсткий зворотний зв'язок діє на систему як у
перехідному, так і в сталому режимі, тобто ![]() ,
і реалізується він безінерційною або інерційною ланкою. Гнучкий зворотний
зв'язок діє лише в перехідних режимах. Реалізується він ланкою що диференціює,
з передатною функцією
,
і реалізується він безінерційною або інерційною ланкою. Гнучкий зворотний
зв'язок діє лише в перехідних режимах. Реалізується він ланкою що диференціює,
з передатною функцією
![]() ,
,
або ланкою, що інерційно-диференціює
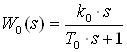 .
.
Паралельний коригувальний пристрій – це третій варіант включення пристрою в АСР (рис. 3).
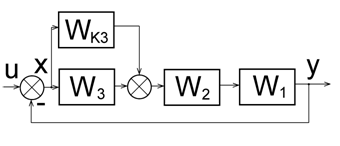
Рис. 3. Паралельне підключення коригувального пристрою.
Включений у такий
спосіб коригувальний пристрій будемо називати прямим паралельним і його
передатну функцію будемо позначати ![]() .
.
Іноді прямий паралельний коригувальний пристрій виявляється дуже зручним, тому що при меншій складності забезпечує потрібне перетворення сигналу керування.
Синтезують
коригувальні пристрої на підставі деякого комплексу вимог до властивостей
системи. Спочатку визначають необхідне значення передатної функції ![]() послідовного
коригувального пристрою. Потім з'ясовують, при яких значеннях передаточних
функцій
послідовного
коригувального пристрою. Потім з'ясовують, при яких значеннях передаточних
функцій ![]() паралельно-зустрічного коригувального
пристрою і
паралельно-зустрічного коригувального
пристрою і ![]() прямого паралельного
коригувального пристрою буде отриманий той же ефект. Після чого вже можна
вирішувати, якій коригувальний пристрій доцільніше створювати.
прямого паралельного
коригувального пристрою буде отриманий той же ефект. Після чого вже можна
вирішувати, якій коригувальний пристрій доцільніше створювати.
Складемо формули для такого розрахунку.
По кожній зі структурних схем (рис. 1,2,3) складемо передаточні функції розімкнутого ланцюга і дорівняємо ці вираження один одному. Одержуємо
 , (3)
, (3)
де ![]() .
.
З (3) визначають формули переходу від одного виду коригувального пристрою до іншого.

Якщо значення передатної
функції ![]() виявляється негативним, то
паралельно-зустрічний коригувальний пристрій повинний включатися у виді
позитивного зворотного зв'язку. При негативному значенні передатної функції
виявляється негативним, то
паралельно-зустрічний коригувальний пристрій повинний включатися у виді
позитивного зворотного зв'язку. При негативному значенні передатної функції ![]() вихідний сигнал прямого
паралельного коригувального пристрою повинний відніматися з вихідного сигналу
ділянки
вихідний сигнал прямого
паралельного коригувального пристрою повинний відніматися з вихідного сигналу
ділянки ![]() .
.
В даний час коригувальні пристрої є основним способом підвищення якості лінійних безупинних систем регулювання по відхиленню. Іноді в системі одночасно використовують два коригувальних пристрої: послідовний і паралельно-зустрічний, або паралельно-зустрічний і прямий паралельний. Таким чином, функції, що повинен виконувати коригувальний пристрій, розподіляються між двома коригувальними пристроями. Ці пристрої можуть бути виконані з більш простих елементів.
Розглянемо один з прикладів практичного застосування коригувального пристрою.
Виконавчий механізм (ВМ) – є невід’ємною частиною АСР. Він перетворює енергію керування, що надходить від регулятора, у механічну енергію переміщення регулюючого органа. При цьому, динамічні властивості АСР в значній мірі залежать від динаміки ВМ. Якщо ВМ має суттєву інерційність, це може викликати появу перерегулювання в роботі АСР. У момент часу, коли сигнал завдання на вході регулятора дорівнює сигналу зворотного зв’язку, регулятор мусить відключатися. Однак ВМ не може раптово зупинитися і продовжує рух. На вхід технологічного об’єкту керування (ТОК) поступає сигнал, який визначається лише неідеальністю ВМ, тому є “паразитним”. Це призводить до того, що на виході ТОК змінюється сигнал. Для знищення цього сигналу необхідно включення АСР в роботу. Подолати це явище можна за допомогою паралельно-зустрічного коригувального пристрою, якій здійснює допоміжній зворотній зв’язок за положенням штока чи вихідного валу ВМ. Такі зв’язки дозволяють зменшити інерційний вибіг ВМ, що покращує роботу системи в цілому [8]. На рис. 4 представлена структурна схема АСР при охоплені ВМ зворотнім зв’язком.
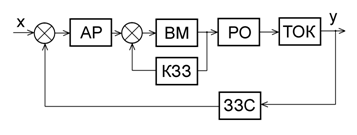
Рис. 4. Структурна схема АСР при охопленні виконавчого механізму зворотнім зв’язком за положенням штока (вихідного валу)
У системі задіяні такі блоки: АР – автоматичний регулятор; ВМ – виконавчий механізм; РО – регулюючий орган; ТОК – технологічний об’єкт керування; КЗЗ – коригувальний зворотній зв’язок; ЗЗС – зворотній зв’язок системи.
2.Практична частина
Завдання:
1. За одержаними даними розробити структурну схему одноконтурної АСР.
2. Розрахувати еквівалентну передаточну функцію АСР.
3. Побудувати перехідний процес для розробленої АСР.
4. Розробити структурну схему одноконтурної АСР, з підключенням коригувального зворотного зв’язку.
5. Розрахувати еквівалентну передаточну функцію АСР з коригувальним зворотнім зв’язком.
6. Побудувати перехідний процес для АСР з коригувальним зворотнім зв’язком.
7. Порівняти перехідні процеси АСР без коригувального зворотного зв’язку, та із коригувальним зворотнім зв’язком.
8. Зробити висновки щодо впливу коригувального зворотного зв’язку на якість роботи АСР.
Рішення:
Будемо вважати, що елементи АСР (рис. 4) мають такі передаточні функції:
- Автоматичний регулятор
![]() .
.
- Виконавчий механізм
![]() .
.
- Регулюючий орган
![]() .
.
- Технологічний об’єкт керування
![]() .
.
- Коригувальний зворотній зв’язок
![]() .
.
- Зворотній зв’язок системи
![]() .
.
Розрахуємо передаточну функцію одноконтурної АСР без коригувального зворотного зв’язку.
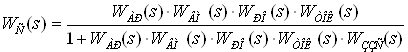 . (4)
. (4)
Підставивши значення передаточних функцій окремих елементів АСР, отримаємо таку передаточну функцію:
![]() . (5)
. (5)
Функція перехідного процесу має вигляд:
![]()
На рис. 5 приведена крива перехідного процесу АСР без коригувального зворотного зв’язку.
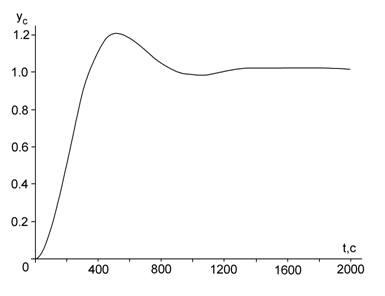
Рис. 5. Крива перехідного процесу одноконтурної АСР без коригувального зворотного зв’язку
Розрахуємо передаточну функцію системи (рис. 4) при охоплені ВМ коригувальним зворотним зв’язком.
Спочатку розрахуємо передаточну функцію ВМ при охоплені його коригувальним зворотним зв’язком.
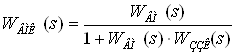 .
.
Тепер підставимо одержане вираження у передаточну функцію системи (4) замість передаточної функції для ВМ. Після цього передаточна функція системи набуде такого вигляду:
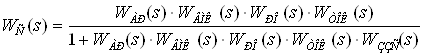 .
.
Підставивши конкретні значення для передаточних функцій окремих елементів і зробив відповідні перетворення, отримаємо передаточну функцію такого вигляду:
![]() . (6)
. (6)
Функція перехідного процесу має вигляд:
![]()
На рис. 6 приведена крива перехідного процесу АСР при охоплені ВМ коригувальним зворотним зв’язком.
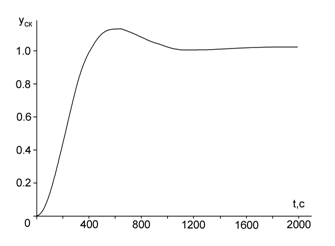
Рис. 6. Крива перехідного процесу АСР при охоплені ВМ коригувальним зворотним зв’язком
Порівняв передаточні функції одноконтурної АСР без коригувального зворотного зв’язку (5), та системи з охопленням ВМ коригувальним зворотним зв’язком, можна зробити такі висновки:
- Структура системи після введення коригувального зворотного зв’язку не змінилась.
- Збільшилось відношення постійної часу першого порядку до квадратного кореню з постійної часу другого порядку, що засвідчує зменшення коливальності системи. У свою чергу це має призводити до зменшення перерегулювання в системі.
Для підтвердження цих висновків, порівняємо графіки перехідних процесів систем.
На рис. 7 приведені криві перехідних процесів АСР без коригувального пристрою, та з охопленням ВМ коригувальним зворотним зв’язком.
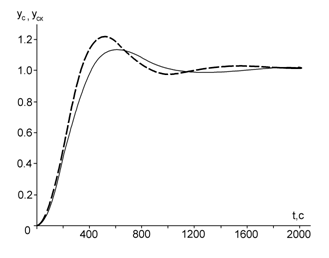
Рис. 7. Криви перехідних процесів АСР: пунктирна лінія – без коригувального зворотного зв’язку; суцільна лінія – при охоплені ВМ коригувальним зворотним зв’язком
Висновок
Порівняння кривих перехідних процесів АСР без коригувального зворотного зв’язку та із охопленням ВМ коригувальним зворотним зв’язком підтверджує покращення характеристик системи. Введення коригувального зворотного зв’язку зменшує ступінь коливальності системи, перерегулювання, а також час регулювання.
При проведенні розрахунків бажано користуватись пакетами прикладних програм для виконання математичних розрахунків на комп’ютері. До їх складу входять Maple, MathCAD і др. Відповідні функції, які реалізовані в даних пакетах, дозволяють легко робити зворотні перетворення Лапласа, переходячи від передаточної функції до функції часу, а також будувати графіки перехідних процесів.
При застосуванні пакетів прикладних програм можуть виникнути труднощі із реалізацією елементів чистого запізнення. В цьому випадку можна розкладати функцію елемента чистого запізнення в ряд Тейлора й брати тільки його лінійну частину.
Література
1. Кулаков М.В. Технологические измерения и приборы для химических производств. – М.: Машиностроение, 1983. – 424 с.
2. Фарзане Н.Г., Илясов Л.В., Азим-Заде А.Ю. Технологические измерения и приборы. – М.: Высш. шк., 1989. – 456 с.
3. Полоцкий Л.М., Лапшенков Г.И. Основы автоматики и автоматизации технологических процессов в химической промышленности. Руководство к лабораторным работам. /Под ред. Н.И. Гальперина. – М.: Химия, 1973. – 320 с.
4. Дианов В.Г. Технологические измерения и контрольно-измерительные приборы химических производств. – М.: Химия, 1973. – 328 с.
5. Стенцель Й.І. Математичне моделювання технологічних об’єктів керування. – К.: ІСДО, 1993. – 328 с.
6. Жданов Л.С., Жданов Г.Л. Физика. – М.: Наука. Главная редакция физико-математической литературы, 1987. – 512 с.
7. Теория автоматического управления: Учеб. для вузов в 2-х ч. Ч 1. /Н.А. Бабаков, А.А. Воронов, А.А. Воронова и др.; Под ред. А.А. Воронова. – М.: Высш. шк., 1986. – 367 с.
8. Клюев А.С., Минаев. Наладка систем контроля и автоматического регулирования. – Л.: Стройиздат, 1980. – 280 с.
9. Богородицкий Н.П., Пасынков В.В., Тареев Б.М. Электротехнические материалы. – Л.: Энергоатомидат, 1985. – 304 с.
10. Дульнев Г.Н. Тепло- и массообмен в радиоэлектронной аппаратуре. – М.: Высш. шк., 1984. – 247 с.
11. Манзон Б.М. Maple V Power Edition. – М.: Информационно-издательский дом «Филинъ», 1998. – 240 с.