Контрольная работа: Расчет балки

Задача №1.

привод крутящий момент балка

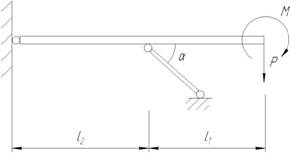
Р = 13 кН, М = 9 кН·м,

l₁ = 0,9 м, l₂ = 1,1 м,

α = 30°.

R_A – ? N_A – ? R_B – ?

Решение

Составим расчетную схему балки, опоры заменим реакциями опор (рис. 1).

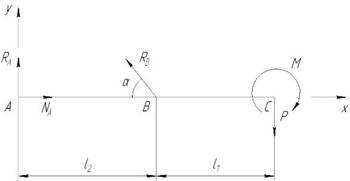
Рис. 1

Составим уравнение моментов относительно точки А:

ΣМ(А) = R_B·sinα·l₂ – M – P(l₁ + l₂) = 0;

Составим уравнение моментов относительно точки B:

ΣМ(B) = – R_A·l₂ – M – P·l₁ = 0;

Проверка:

ΣF_Y = R_B·sinα + R_A – P = 0;

63,6·sin30° – 18,8 – 13 = 0;

0 = 0 – реакции найдены верно.

Составим уравнение сил по оси х:

ΣF_Х = N_A – R_B·cosα = 0;

N_A = R_B·cosα = 63,6·cos30° = 55,1 кH.

Реакции опорного шарнира: R_A и N_A.

Сила, нагружающая стержень по модулю равна R_B и направлена в противоположную сторону.

Задача №2.

М₁ = 440 Н·м, М₂ = 200 Н·м,

М₃ = 860 Н·м, [τ]_кр = 100 МПа,

Ст3, круг, кольцо d₀/d = 0,7

d _кр – ? d₀ – ? d – ?

Решение

Для заданного бруса построим эпюру крутящих моментов (рис. 2).

Заданный брус имеет три участка нагружения.

Возьмем произвольное сечение в пределах I участка и отбросим левую часть бруса.

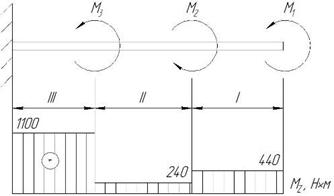
Рис. 2

На оставленную часть бруса действуют моменты М₁ и М_Z^I. Следовательно:

М_Z^I = М₁ = 440 Н∙м.

Взяв произвольное сечение в пределах II участка, и рассматривая равновесие оставленной части бруса получим:

М_Z^II = М₁ – M₂ = 440 – 200 = 240 Н∙м.

Взяв произвольное сечение в пределах III участка, и рассматривая равновесие оставленной части бруса получим:

М_Z^III = М₁ – M₂ + M₃ = 440 – 200 +860 = 1100 Н∙м.

По имеющимся данным строим эпюру крутящих моментов.

Условие прочности:

Отсюда:

Для круга:

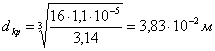
Для кольца:

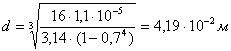
Массы брусьев.

Круг.

Кольцо.

Так как S₂ < S₁, то масса бруса с сечением в форме круга больше, чем с сечением в форме кольца.

Увеличим размер сечения в два раза.

Рассмотрим круг.

При увеличении размера сечения круга в 2 раза, нагрузку на брус можно увеличить в 8 раз.

Затраты материала увеличатся в 4 раза.

Аналогично получаются такие же результаты для сечения в форме кольца, так как формулы схожи.

Задача №3.

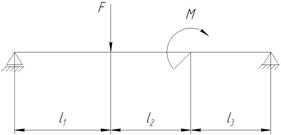
F = 21 кН, М = 13 кН·м,

l₁ = 0,9 м, [δ]_изг = 150 МПа,

l₂ = 0,5 м, l₃ = 0,7 м,

Ст3, швеллер, прямоугольник

h/b = 3

швеллер – ? h – ? b – ?

Решение

Отбросив опоры, заменим их действие на балку реакциями R_A и R_В. Определим значение R_A и R_В.

ΣМ_А(F_i) = F·l₁ + M – R_В (l₁ + l₂ + l₃) = 0;

ΣМ_B(F_i) = – F·(l₂ +l₃) + M + R_A (l₁ + l₂ + l₃) = 0;

Проверка:

ΣF_i = R_B + R_A – F = 0;

15,2 + 5,8 – 21 = 0;

0 = 0 – реакции найдены верно.

Балка имеет три участка нагружения.

Возьмем произвольное сечение в пределах I участка:

Q_y^I = R_A = 5,8 кН

М_Х^I = R_A∙z

При z = 0; М_Х^I(0) = 0.

При z = l₁; М_Х^I(0,9) = 5,8∙0,9 = 5,2 кН∙м.

Возьмем произвольное сечение в пределах II участка:

Q_y^II = R_A – F = 5,8 – 21 = -15,2 кН

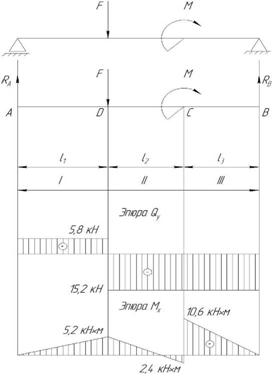
Рис. 3

М_Х^II = R_A∙z – F (z – l₁)

При z = l₁ + l₂; М_Х^II(1,4) = 5,8∙1,4 – 21∙0,5 = -2,4 кН∙м.

В точке, расположенной бесконечно близко справа от точки С:

М_Х^II’ = R_A∙z – F (z – l₁) + M

М_Х^II’ (1,4) = 5,8∙1,4 – 21∙0,5 + 13 = 10,6 кН∙м.

Возьмем произвольное сечение в пределах III участка:

Q_y^III = R_A – F = 5,8 – 21 = -15,2 кН

М_Х^III = R_A∙z – F (z – l₁) + M

В точке В: М_Х^III = 0.

По имеющимся данным строим эпюры поперечных сил и изгибающих моментов (рис. 3).

Условие прочности:

Отсюда:

Швеллер.

Берем швеллер №14а с W_X = 77,8 см³, S_X = 45,1 см³ = 4,51∙10^-5 м³.

Прямоугольник.

Так как S_Х < S, то масса балки с сечением в форме прямоугольника больше, чем масса балки из швеллера.

Увеличим размеры прямоугольного сечения в два раза.

- затраты материала увеличатся в два раза.

- нагрузку можно увеличить в два раза.

- затраты материала увеличатся в два раза.

- нагрузку можно увеличить в четыре раза.

Задача №4

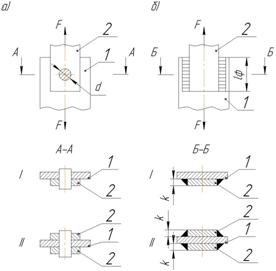
l_ф = 100 мм, [τ]_ср = 80 МПа,

k = 6 мм, [τ]’_ср = 100 МПа.

d – ?

Решение

Найдем силу F из условия прочности швов при срезе.

I схема.

F = 0,7·[τ]’_ср ·k·2·l_ф = 0,7·100·10⁶·0,006·2·0,1 = 84 кН

II схема.

F = 0,7·[τ]’_ср ·k·4·l_ф = 0,7·100·10⁶·0,006·4·0,1 = 168 кН

Условие прочности на срез:

Определим диаметр пальца из условия прочности при срезе.

I схема.

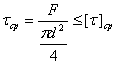
Берем d = 37 мм.

II схема.

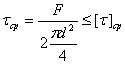
Берем d = 37 мм.

Задача №5.

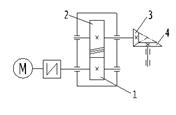
Р_дв = 4 кВт, ω_дв = 158 рад/с, Z₃ = 24, Z₄ = 36, ω_вых = 38 рад/с, η_ц = 0,97, η_к = 0,95,

а = 140 мм, ψ = 0,5.

η_общ – ? U_общ – ? Р_i – ? M_i – ?

Решение

Общий КПД привода:

η_общ = η_ц · η_к · η_м · η_п³

η_ц. – КПД зубчатой цилиндрической передачи;

η_к. – КПД зубчатой конической передачи;

η_м = 0,98 – КПД муфты;

η_п = 0,98…0,99; принимаем η_п = 0,98 – КПД пары подшипников качения.

η_общ = 0,97 · 0,95 · 0,98 · 0,98³ = 0,85

Общее передаточное отношение привода:

U_общ = ω_дв / ω_вых = 158 / 38 = 4,16

Передаточное отношение конической передачи:

U_к = Z₄ / Z₃= 36 / 24 = 1,5

Передаточное отношение цилиндрической передачи:

U_ц = U_общ / U_к = 4,16 / 1,5 = 2,77

Вал двигателя.

Р_дв = 4 кВт;

ω_дв = 158 рад/с;

Т_дв = Р_дв / ω_дв = 4000 / 158 = 25,32 Н·м.

Быстроходный вал редуктора.

Р₁ = Р_дв · η_м · η_п = 4 · 0,98 · 0,98 = 3,84 кВт;

ω₁ = ω_дв = 158 рад/с;

Т₁ = Т_дв · η_м · η_п = 25,32 · 0,98 · 0,98 = 24,32 Н·м.

Тихоходный вал редуктора.

Р₂ = Р₁ · η_п · η_ц = 3,84 · 0,98 · 0,97 = 3,65 кВт;

ω₂ = ω₁ / U_ц = 158 / 2,77 = 57,04 рад/с;

Т₂ = Т₁ · U_ц · η_ц. · η_п = 24,32 · 2,77 · 0,98 · 0,97 = 64,04 Н·м.

Выходной вал привода.

Р₃ = Р₂ · η_п · η_к = 3,65 · 0,98 · 0,95 = 3,4 кВт;

ω_вых = 38 рад/с;

Т₃ = Т₂ · U_к · η_к. · η_п = 64,04 · 1,5 · 0,98 · 0,95 = 89,43 Н·м.

Данный привод имеет две ступени. Первая ступень – косозубый цилиндрический редуктор. Вторая ступень – открытая коническая передача. Электродвигатель соединен с быстроходным валом редуктора муфтой. Основные технические характеристики привода:

·  КПД – 0,85;

·  Общее передаточное число – 4,16;

·  Вращающий момент на выходном валу – 89,43 Н·м;

·  Угловая скорость выходного вала – 38 рад/с.

Цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном диаметре, называют косозубыми. При работе такой передачи зубья входят в зацепление не сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка распределяется на несколько зубьев. В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность работы передачи и уменьшается шум. В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.

Недостатками косозубых колёс можно считать следующие факторы:

При работе косозубого колеса возникает механическая сила, направленная вдоль оси, что вызывает необходимость применения для установки вала упорных подшипников;

Увеличение площади трения зубьев (что вызывает дополнительные потери мощности на нагрев), которое компенсируется применением специальных смазок.

Основные формулы для расчета косозубой передачи приведены ниже.

Конические зубчатые колеса применяют в передачах, у которых оси валов пересекаются под некоторым углом. Наиболее распространены передачи с углом 90°.

Аналогами начальных и делительных цилиндров цилиндрических передач в конических передачах являются начальные и делительные конусы с углами δ₁ и δ₂.

При коэффициентах смещения инструмента х₁ + х₂ = 0 начальные и делительные конусы совпадают. Конусы, образующие которых перпендикулярны образующим елительных конусов, называют дополнительными конусами. Сечение зубьев дополнительным конусом называют торцовым сечением. Различают внешнее, внутреннее и среднее торцовые сечения.

Основными габаритными размерами для конических передач являются d_e2 и R_e, а нагрузка характеризуется моментом Т₂ на ведомом валу. Основные зависимости:

,

,

,

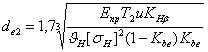d’_m1 = d’_e1(R’_e – 0,5b’)/R’_e,

m’_nm = m’_tmcosβ_n,

d_m1 = m_tmz₁, d_m2 = m_tmz₂.

Из различных типов конических колес с непрямыми зубьями на практике получили распространение колеса с косыми или тангенциальными зубьями и колеса с круговыми зубьями. Преимущественное применение получили колеса с круговыми зубьями. Они менее чувствительны к нарушению точности взаимного расположения колес, их изготовление проще.

Конические передачи применяются при пересекающихся валах. Конические передачи дорогие. Выгодны не прямозубые, а косозубые колеса, так как они позволяют уменьшить габариты и массу.

Выполним геометрический расчет передачи редуктора.

Модуль зацепления:

m = (0,01–0,02) α = 1,4 – 2,8 мм, принимаем m = 2 мм.

Ширина колеса:

b₂ = ψ · α = 0,5 · 140 = 70 мм

b₁ = b₂ + 5 = 70 + 5 = 75 мм – ширина шестерни.

Минимальный угол наклона зубьев:

β_min = arcsin = arcsin = 5,7°

При β = β_min сумма чисел зубьев z_c = z₁ + z₂ = (2α/m) cos β_min = (2 · 140/2) cos 5,7°= 139,3

Округляем до целого: z_c = 139

Угол наклона зубьев:

β = arccos = arccos = 6,85°,

при нем z_c = (2 · 140/2) cos 6,85° = 139

Число зубьев шестерни:

z₁ = z_c / (U_ц + 1) = 139 / (2,77 + 1) ≈ 37

z₂ = 139 – 37 = 102 – колеса.

Передаточное число:

U_ф = 102 / 37 = 2,76, отклонение ΔU = 0,02U – допустимо.

Диаметры делительных окружностей:

d₁ = m z₁ /cos β = 2 · 37 / cos 6,85° = 74,5 мм – шестерни;

d₂ = m z₂ /cos β = 2 · 102 / cos 6,85° = 205,5 мм – колеса.

Торцевой (окружной) модуль:

m_t = m /cos β = 2 / cos 6,85° = 2,014

Диаметры вершин зубьев:

d_а1 = d₁ + 2m = 74,5 + 2 · 2 = 78,5 мм;

d_а2 = d₂ + 2m = 205,5 + 2 · 2 = 209,5 мм.

Диаметры впадин зубьев:

d_f1 = d₁ - 2,5m = 74,5 – 2,5 · 2 = 69,5 мм;

d_f2 = d₂ - 2,5m = 205,5 – 2,5 · 2 = 200,5 мм.