Контрольная работа: Расчет режимов и характеристик электрических цепей с операционным усилителем
Расчёт режимов и характеристик электрических цепей с операционным усилителем
1. Задание
1. Для заданной схемы (рис 1.) рассчитать передаточную функцию цепи в смысле коэффициента передачи напряжения H(p).
Схема электрическая: Исходные данные:
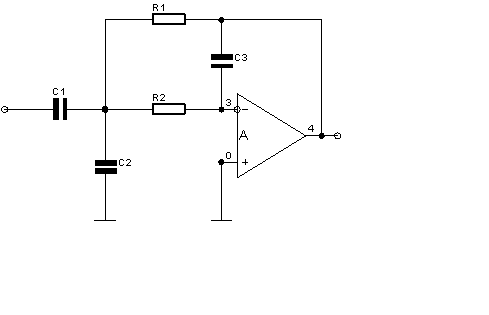
R1=R 2=10кОм;
C1=0.008мкФ;
C2 =0,002мкФ;
C3=0.01мкФ;
2. Построить карту передаточной функции и проверить H(p) по схеме.
3. Записать выражение частотных характеристик передаточной функции.
Комплексная частотная характеристика передаточной функции H(jω).
Амплитудо-частотная характеристика передаточной функции H(ω).
Фазочастотная характеристика передаточной функции φ(ω).
4. Рассчитать и построить временные характеристики.
Переходная характеристика передаточной функции h(t).
Импульсная характеристика передаточной функции g(t).
5. Рассчитать и построить реакцию цепи Uвых(t) на прямоугольный импульс с амплитудой напряжения Um(мВ).
2. Анализ схемы
Операционный усилитель в идеальном случае представляет собой усилитель с:
1. Бесконечно большим входным сопротивлением.
2. Бесконечно малым выходным сопротивлением.
3. Бесконечно большим коэффициентом усиления.
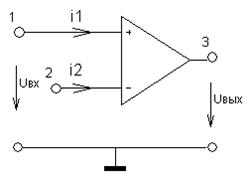
Схема эквивалентная ОУ:
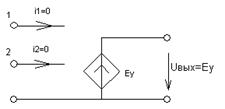
По первому свойству
можно предположить, что ток i1 практически равен нулю. Аналогично ток i2=0 Учитывая 3-е
свойство, можно записать, что ![]()
![]() ,
, ![]() . Напряжение на выходе – конечная
величина, следовательно
. Напряжение на выходе – конечная
величина, следовательно ![]() (Основное
расчетное свойство для цепи с ОУ) Заданная схема содержит 2 накопителя, т.е.
рассматриваемая цепь 2-го порядка. Согласно заданию, искомой ПФ является
Коэффициент передачи напряжения (КПН):
(Основное
расчетное свойство для цепи с ОУ) Заданная схема содержит 2 накопителя, т.е.
рассматриваемая цепь 2-го порядка. Согласно заданию, искомой ПФ является
Коэффициент передачи напряжения (КПН): 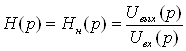 -ОКПН.
-ОКПН.
3. Расчет передаточной функции
Схема расчетная:
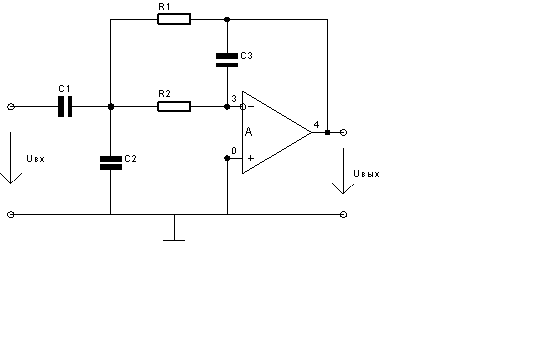
Шаг 1. Расчётная операторная схема

Шаг 2. Система уравнений методом узловых потенциалов.
Основное расчётное соотношение φ3(p)=0;
φ1(p)=Eвх(p); φ4(p)=Eу(p);
![]()

![]()
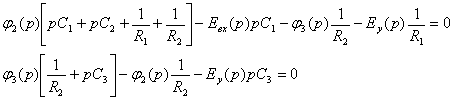
![]()
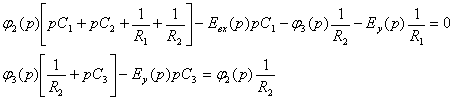
![]()
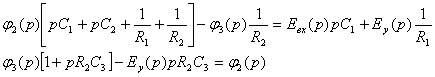

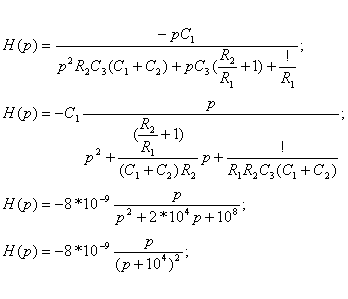
Ответ: ![]() .
.
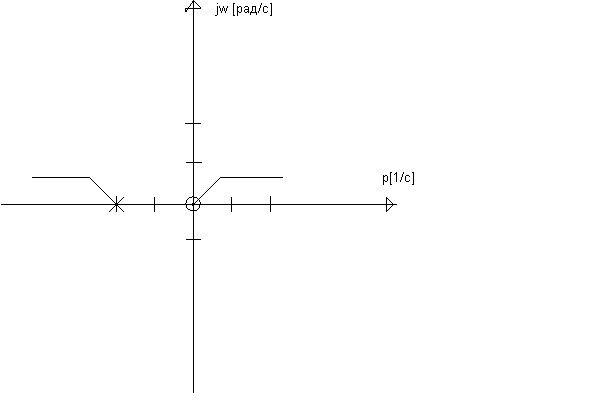
4. Карта передаточной функции, проверка передаточной функции по схеме
Картой ПФ называют чертеж на комплексной плоскости, где отмечены нули, полюса и масштабные коэффициенты.
Ноль: ![]()
Полюса: ![]()
![]()
![]()
![]()
![]()
![]()
Проверка ПФ по схеме: критерием правильности ПФ является полином знаменателя 2-го порядка. Полюса расположены в левой части полуплоскости. Они отрицательны, что соответствует корням схемы.
Проведем проверку в ряде точек:
1. ![]() ;
;
По ПФ ![]()
По схеме ![]()
![]()
2. ![]()
По ПФ ![]()
По схеме ![]()
![]()
5. Расчет частотных характеристик ПФ

Построение АЧХ и ФЧХ по карте нулей и полюсов.
![]()
![]()
|
|
|
|
|
|
| 0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
| 0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
АЧХ:
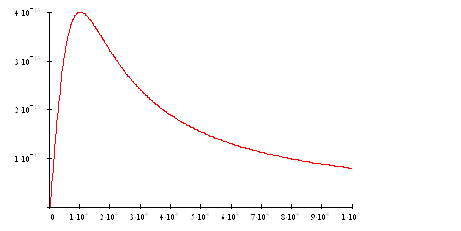
ФЧХ:
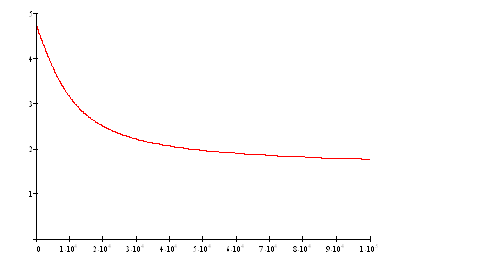
6. Временные характеристики
Временными характеристиками электрической цепи является переходная и импульсная характеристики.
ПХ: ![]()
ИХ: ![]()
Согласно заданию, временные характеристики получим по найденной передаточной функции H(p).
![]()
Импульсная
характеристика ![]() переходная
характеристика
переходная
характеристика![]()
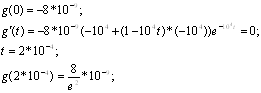
Расчёт импульсной характеристики
![]() Перейдём к оригиналу.
Перейдём к оригиналу. ![]()
![]()
![]()
Так как степени полиномов числителя и знаменателя равны, то дробь неправильная. Из неё можно выделитьцелую часть и простую дробь.
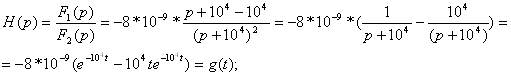
Ответ: ИХ ![]() 1/c.
1/c.
Расчёт переходной характеристики
![]()
![]()
Ответ: ПХ ![]() б/р.
б/р.
Графики:
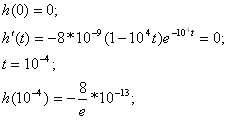
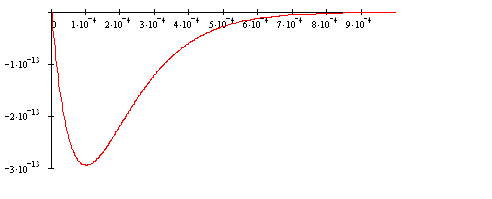
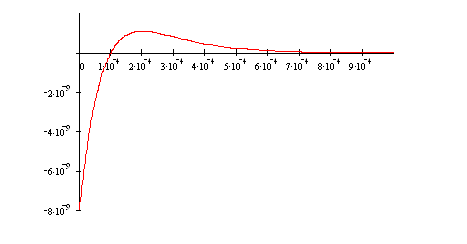
Проверка по соотношению:
![]()
Вывод: Полученные ИХ и ПХ друг другу соответствуют. Значит они верны.
7. Расчёт реакции цепи на прямоугольный импульс
Амплитуда
импульса ![]() Длительность:
Длительность: ![]()
![]()
Воздействие:
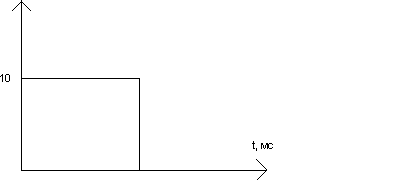
![]()
![]()
Расчёт
проведём с помощью ПХ h(t). Поскольку h(t) численно равна реакции на ступеньку, то ![]()
Ответ: 1-й интервал:
0<t<1.5*10-4,
![]()
2-ой
интервал: 1.5*10-4<t<∞, ![]()