Курсовая работа: Расчёт и анализ нерекурсивного цифрового фильтра
1. Краткое математическое описание методов расчёта
1.1. Общие положения
Цифровой фильтр полностью описывается своим разностным уравнением:
![]() (1)
(1)
Для
нерекурсивного цифрового фильтра ![]() и
уравнение принимает вид:
и
уравнение принимает вид:
![]() (2)
(2)
Зная коэффициенты разностного уравнения, можно легко получить выражение для передаточной функции фильтра (для НЦФ):
![]() (3)
(3)
Для образа выходного сигнала НЦФ справедливо выражение
![]() , (4)
, (4)
где ![]() – z-преобразования выходного
и входного сигналов фильтра.
– z-преобразования выходного
и входного сигналов фильтра.
Зная
выражение (4) и учитывая, что z-преобразование функции единичного скачка ![]() равно 1, можно получить
выражение для z-образа
импульсной характеристики
равно 1, можно получить
выражение для z-образа
импульсной характеристики ![]() :
:
![]() (5)
(5)
Из (5) следует, что отсчеты импульсной характеристики НЦФ численно равны коэффициентам разностного уравнения НЦФ, а сама импульсная характеристика и передаточная функция связаны парой z-преобразований (прямым и обратным).
Заменив в (4)
z на ![]() , получим комплексную
частотную характеристику:
, получим комплексную
частотную характеристику:
![]() (6)
(6)
Импульсная характеристика и комплексная частотная характеристика связаны парой преобразований Фурье:
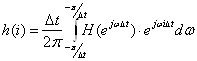 (7)
(7)
![]() (8)
(8)
Из комплексной частотной характеристики можно получить выражения для АЧХ и ФЧХ:
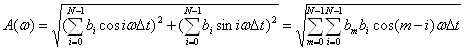 (9)
(9)
![]() (10)
(10)
Во все
вышеприведённые формулы входит интервал квантования ![]() .
Чтобы от него избавиться, частоту обычно нормируют. Это можно сделать с помощью
замены:
.
Чтобы от него избавиться, частоту обычно нормируют. Это можно сделать с помощью
замены:
![]() (11)
(11)
Так как
интервал определения ![]() , то интервал
определения
, то интервал
определения ![]() . Исходными данными для
проектирования фильтра является его АЧХ. Как правило, в зонах неопределённости
АЧХ некоторым образом доопределяют с тем, чтобы избежать явления Гиббса («выбросы»
характеристики в точках разрыва первого рода – «скачках»). В простейшем случае
доопределить АЧХ можно линейным законом. В этом случае АЧХ проектируемого
полосового фильтра будет выглядеть таким образом.
. Исходными данными для
проектирования фильтра является его АЧХ. Как правило, в зонах неопределённости
АЧХ некоторым образом доопределяют с тем, чтобы избежать явления Гиббса («выбросы»
характеристики в точках разрыва первого рода – «скачках»). В простейшем случае
доопределить АЧХ можно линейным законом. В этом случае АЧХ проектируемого
полосового фильтра будет выглядеть таким образом.
Аналитически АЧХ будет записываться в виде:
 (12)
(12)
При
проектировании часто полагают, что ФЧХ фильтра является линейной. В [1]
показывается, что в этом случае импульсная характеристика фильтра является либо
симметричной (![]() ), либо
антисимметричной (
), либо
антисимметричной (![]() ). Учитывая, что
порядок фильтра
). Учитывая, что
порядок фильтра ![]() может быть
чётным и нечётным, существует четыре вида ИХ с линейной ФЧХ:
может быть
чётным и нечётным, существует четыре вида ИХ с линейной ФЧХ:
1. N – нечётное, ИХ – симметричная
2. N – чётное, ИХ – симметричная
3. N – нечётное, ИХ – антисимметричная
4. N – чётное, ИХ – антисимметричная
цифровой фильтр выборка частотный
1.2 Метод частотной выборки
Основная идея метода частотной выборки – замену в выражениях (7) и (8) непрерывную частоту дискретизированной. В этом случае выражения (7) и (8) превращаются в пару дискретных преобразований Фурье:
![]() (13)
(13)
![]() (14)
(14)
Существует 2 метода дискретизации частоты (выражения записаны для нормированной частоты):
![]() (15)
(15)
![]() (16)
(16)
Выражения (13) и (14) записаны для первого метода дискретизации частоты. По условию задания необходимо использовать второй метод дискретизации частоты, в этом случае выражение (14) приобретает вид:
![]() (17)
(17)
Из (17) следует, что для определения импульсной характеристики необходимо знать частотную характеристику. Её можно записать в показательной форме:
![]() (18)
(18)
![]() (19)
(19)
При чётном N:
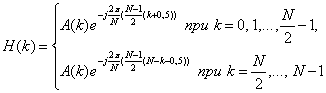 (20)
(20)
При нечётном N:
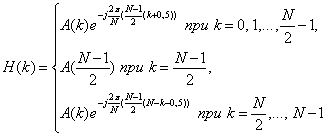 (21)
(21)
Подставляя
вместо ![]()
![]() , по выражениям (20) и (21)
можно найти
, по выражениям (20) и (21)
можно найти ![]() , а из (17) –
, а из (17) – ![]() .
.
1.3 М етод наименьших квадратов
При расчете коэффициентов импульсной характеристики используется формула вида:

после чего решается система уравнений:
![]() и находятся коэффициенты
Ск.
и находятся коэффициенты
Ск.
Далее из найденных Ск можно найти коэффициенты импульсной характеристики:
![]()
![]()
![]()
2. Расчётная часть
2.1 Расчёт методом частотной выборки
2.1.1 Расчёт импульсной характеристики
Расчёт импульсной характеристики для нечётных N осуществлялся по формулам (21) и (17), для чётных – по формулам (20) и (17). Результаты расчёта импульсной характеристики для N=15, 25 и 32 представлены в таблице 1.
Таблица 1. Результаты расчёта импульсной характеристики методом частотной выборки
|
i |
Значение импульсной
характеристики |
||
| N=15 | N=25 | N=32 | |
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
0,081 -0,013 0,025 -0,052 -0,303 0,03 0,46 0,03 -0,303 -0,052 0,025 -0,013 0,081 |
0,001497 0,001756 -0,02 -0,007456 -0,007554 0,028 0,061 -0,004905 0,034 -0,048 -0,297 -0,035 0,45 0,035 -0,297 -0,048 0,034 -0,004905 0,061 0,028 -0,007454 -0,007456 -0,02 0,001756 0,001497 |
0,001488 -0,008534 0,008698 -0,000256 0,003711 -0,011 0,015 -0,007875 -0,001266 0,053 0,029 0,0009025 0,04 -0,193 -0,224 0,321 0,321 -0,224 -0,193 0,04 0,0009025 0,029 0,053 0,001266 -0,007875 -0,015 -0,011 -0,003711 -0,000256 0,008698 -0,0008534 0,001488 |
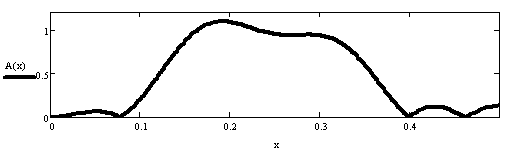
2.1.2 Расчёт АЧХ и ФЧХ
Расчёт АЧХ и
ФЧХ осуществлялся по формулам (9) и (10) для 50 значений частоты ![]() , взятой с шагом 0,01 (
, взятой с шагом 0,01 (![]() ). На рисунках приведены
графики рассчитанной АЧХ фильтра.
). На рисунках приведены
графики рассчитанной АЧХ фильтра.
Для расчёта точности аппроксимации запишем функцию ошибки аппроксимации:
![]() , (32)
, (32)
![]()
В таблице 2
приведены результаты расчёта точности аппроксимации ![]() .
.
Таблица 2. Результаты расчета точности аппроксимации для метода частотной выборки
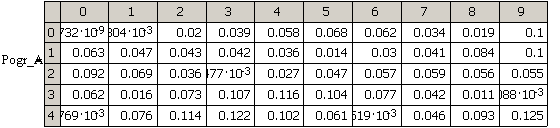
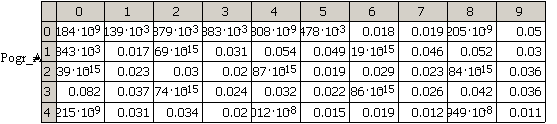
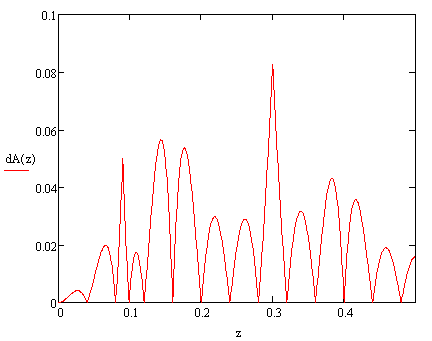
График функции точности аппроксимации для N=25
Максимальные ошибки аппроксимации (абсолютная погрешность) для трёх значений N приведены в таблице 3:
Абсолютная погрешность аппроксимации АЧХ, рассчитанной методом частотной выборки
|
Абсолютная погрешность аппроксимации АЧХ |
||
| N=13 | N=25 | N=32 |
| 0,125 | 0,082 | 0,049 |
2.2 Расчёт методом наименьших квадратов
2.2.1 Расчёт импульсной характеристики
Результаты расчёта импульсной характеристики для N=13, 25 и 32 представлены в таблице. Учитывая симметрию импульсной характеристики, приведена только половина отсчётов.
Результаты расчёта импульсной характеристики методом наименьших квадратов
|
i |
Значение импульсной
характеристики |
||
| N=13 | N=25 | N=32 | |
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
0,055 -0,004049 0,035 -0,042 -0,296 0,03 0,45 |
-0,003929 -0,003499 -0,012 0,008469 -0,008832 -0,026 0,055 0,035 -0,042 -0,296 0,03 0,45 |
0,002208 -0,005211 0,003349 0,003189 -0,003929 -0,003499 -0,012 -0,008469 -0,008832 0,026 0,055 -0,004049 0,035 -0,042 -0,296 0,45 0,45 |
2.2.2 Расчёт АЧХ и ФЧХ
Расчёт АЧХ и
ФЧХ осуществлялся по формулам (9) и (10) для 50 значений частоты ![]() , взятой с шагом 0,01 (
, взятой с шагом 0,01 (![]() ).
).
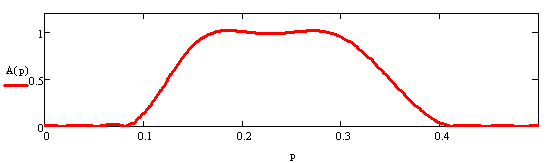
Заданная по условию и рассчитанная АЧХ фильтра для N=25 (метод наименьших квадратов)
2.2.3 Расчёт точности аппроксимации
Точность
аппроксимации оценивалась по формуле (32). В таблице (5) приведены результаты
расчёта ![]()
Результаты расчета точности аппроксимации для метода наименьших квадратов
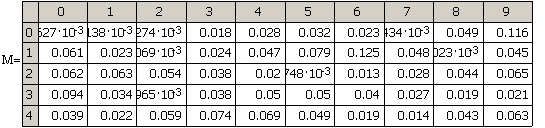
В таблице 6 приведена максимальная (абсолютная) погрешность аппроксимации для различных значений N.
Абсолютная погрешность аппроксимации для метода наименьших квадратов
|
Абсолютная погрешность аппроксимации АЧХ |
||
| N=135 | N=25 | N=32 |
| 0,125 | 0,057 | 0,051 |
2.3 Сравнение методов расчёта
Сравнивая результаты расчётов точности аппроксимации, приведённые в таблицах 2 и 6, можно сделать вывод, что метод наименьших квадратов обеспечивает более точную аппроксимацию при N=25 амплитудно-частотной характеристики по сравнению с методом частотной выборки. С увеличением порядка фильтра N точность аппроксимации увеличивается для обоих методов, но точность метода наименьших квадратов начинает уменьшаться по сравнению с методом частотной выборки.
Заключение
В данной курсовой работе был рассмотрен расчёт нерекурсивного цифрового фильтра двумя методами: методом наименьших квадратов и методом частотной выборки. Результаты расчётов точности аппроксимации для каждого метода позволяют сделать следующие выводы:
· Точность аппроксимации увеличивается с увеличением N (порядка фильтра)
· Метод наименьших квадратов обеспечивает более точную аппроксимацию при средних значениях N.