Реферат: Моделирование динамики урожайности зерновых культур в Нижнем Поволжье методом многократного выравнивания
Построение эконометрических моделей и адекватное оценивание их параметров служит основой для экономического анализа и прогнозирования, создавая возможность для принятия обоснованных экономических решений.
При изучении динамики необходимо четко разделить два ее элемента - тенденцию и колеблемость [1 - 3]. Акцент в изучении колеблемости нестационарных временных рядов смещается в сторону вариации отклонений фактических значений от значений, определяемых функцией тренда для каждого момента. Возникновение случайно распределенной во времени колеблемости зависит от того, насколько правильно выбран тип функции у=f (x) и как точно удалось определить ее параметры. В этой связи интересным является предложение М.М. Юзбашева - изучать колеблемость урожайности культур с помощью статистических характеристик, основанных на расчетах с применением скользящего тренда [2].
Целью настоящей работы является проведение анализа и краткосрочного прогнозирования урожайности зерновых культур. В качестве исходных данных принимались временные ряды урожайности зерновых культур по Волгоградской области за 1953-2007 гг. по данным Волгоградстата (табл.1). Урожайность зерновых культур в Волгоградской области за последние десятилетия увеличилась почти втрое и в среднем составила 11,86 ц/га при стандартном отклонении 5,04 ц/га.
Таблица 1 - Урожайность зерновых культур по Волгоградской области
| Год | Урожайность, ц/га | Год | Урожайность, ц/га | Год | Урожайность, ц/га | Год | Урожайность, ц/га | Год | Урожайность, ц/га |
| 1953 | 4,8 | 1964 | 14 | 1975 | 3,8 | 1986 | 10,6 | 1997 | 14,8 |
| 1954 | 3,6 | 1965 | 9,2 | 1976 | 19,2 | 1987 | 13,2 | 1998 | 4,7 |
| 1955 | 8,4 | 1966 | 12,5 | 1977 | 10,2 | 1988 | 18,5 | 1999 | 7 |
| 1956 | 4,8 | 1967 | 11,2 | 1978 | 19,7 | 1989 | 18,4 | 2000 | 12,2 |
| 1957 | 3,9 | 1968 | 12,9 | 1979 | 6,8 | 1990 | 20,6 | 2001 | 17 |
| 1958 | 13,7 | 1969 | 6,4 | 1980 | 11,9 | 1991 | 14,4 | 2002 | 16,1 |
| 1959 | 5,5 | 1970 | 17,5 | 1981 | 8,2 | 1992 | 15,4 | 2003 | 15,2 |
| 1960 | 10,4 | 1971 | 10,8 | 1982 | 10,2 | 1993 | 20,1 | 2004 | 19,5 |
| 1961 | 10 | 1972 | 4,5 | 1983 | 13,1 | 1994 | 12 | 2005 | 18,5 |
| 1962 | 14,3 | 1973 | 17,2 | 1984 | 4,1 | 1995 | 5,9 | 2006 | 17,1 |
| 1963 | 6,1 | 1974 | 16 | 1985 | 14,1 | 1996 | 8,8 | 2007 | 13,5 |
Скользящая одиннадцатилетняя средняя, сглаживая колебания отдельных уровней, отчетливо показывает тенденцию повышения уровней. Если разбить ряд на пять частей, то средние уровни также подтверждают этот вывод: за 1953-1563 гг. средний уровень равен 7,77; за 1964-1974 гг. - 12,02; за 1975-1985 гг. - 11,03; за 1986-1996 гг. - 14,35; за 1997-2007 гг. - 14,15. Существенного различия в величине повышения среднегодовых уровней нет.
Для выявления типа тренда была проведена проверка статистической гипотезы о постоянстве того или иного показателя динамики, и, в первую очередь, гипотезы о линейной форме уравнения тренда, т.е. о несущественности различий цепных абсолютных изменений [2].
По ряду сглаженных уровней
вычислялись абсолютные цепные приросты, которые разбивались на два подпериода. Для
каждого подпериода рассчитывали среднюю ![]() , ее квадратическое
отклонение s∆k и среднюю ошибку среднего изменения m∆k. Существенность различий между средними абсолютными изменениями проверим
по t-критерию Стьюдента.
, ее квадратическое
отклонение s∆k и среднюю ошибку среднего изменения m∆k. Существенность различий между средними абсолютными изменениями проверим
по t-критерию Стьюдента.
Средняя случайная ошибка разностей двух выборочных средних оценок:
![]() (1)
(1)
Критерий Стьюдента для оценки существенности различия двух среднегодовых приростов:
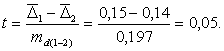
Критическое значение t-критерия при уровне значимости 0,05 и при 42 степенях свободы равно 2,018. Фактическое значение меньше. Следовательно, гипотеза о равенстве приростов не отклоняется и тенденцию динамики на всем протяжении ряда можно считать линейной.
Однократное аналитическое выравнивание неполно освобождает параметры тренда от влияния колеблемости. Для дальнейшего исключения искажающего влияния колебаний на параметры тренда можно применить метод многократного скользящего выравнивания [2].
Сущность методики состоит в том, что параметры тренда вычисляются не сразу по всему ряду длиной n периодов времени, а скользящим методом - сначала за первые m периодов времени, затем за период от 2-го до от m+1, далее от 3-го до (m+2) - го уровня и т.д.
Если число исходных уровней ряда равно n, а длина скользящей базы расчета параметров равна m, то число скользящих баз составит: L=n+1-m.
Смысл многократного скользящего выравнивания в том, что при последовательных сдвигах базы расчета параметров на концах ее и в середине окажутся разные уровни с разными по знаку и величине отклонениями от тренда.
Поэтому при одних сдвигах базы параметры будут завышаться, при других - занижаться, а при последующем усреднении значений параметров по всем сдвигам базы расчета произойдет дальнейшее взаимопогашение искажений параметров тренда колебаниями уровней.
Поскольку уже было установлено, что тренд имеет линейную форму, проводим расчет среднегодового абсолютного прироста, т.е. параметра b уравнения линейного тренда, скользящим способом по 39-летним базам:
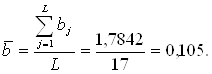
При условии отсчета времени от середины периода свободный член тренда - это средняя величина уровня за период: а = 625,5/55 = 11,86.
Уравнение тренда принимает вид:
![]() (2)
(2)
Расчетное значение F-критерия Фишера равно 5,1 и больше табличного 4,1, что свидетельствует о существенности полученного уравнения.
Проверка случайности остатков модели (2) проводилась по критерию восходящих и нисходящих серий [1].
Для временного ряда отклонений от тренда урожайности зерновых культур было определено 40 серий при максимальной длине каждой - 3 наблюдения. Расчетное значение количества серий составило 30, K0 (n) =6. Таким образом, получены соотношения: 40>30 и 3<6. Это свидетельствует о целесообразности использования линейного тренда в качестве адекватной модели динамического процесса урожайности зерновых за 1953-2007 гг.
Представленная информация свидетельствует о наличии значительной вариации ряда отклонений. Исследования временного ряда отклонений от тренда на соответствие нормальному закону распределения проводились с помощью расчетов коэффициентов асимметрии (A = - 0,102) и эксцесса (E = - 0,883). Следовательно, остатки имеют распределение, близкое к нормальному. В этом случае вероятность того, что отдельные колебания не превысят среднюю величину s (t), составляет 0,68.
Для выявления типа колебаний использовался, предложенный М. Кендэлом прием [2], состоящий в подсчете "поворотных точек" в ряду отклонений от тренда. При этом отклонение, либо большее по алгебраической величине, либо меньшее двух соседних, отмечается точкой.
При маятниковой колеблемости все отклонения, кроме двух крайних, будут поворотными, следовательно, их число составит n-2. При долгопериодических циклах на цикл приходятся один минимум и один максимум, а общее число точек составит: 2 (n/l), где l - длительность цикла. Для случайно распределенной колеблемости во времени число поворотных точек в среднем составит: 2/3 (n-2) [2].
Фактическое число поворотных точек в анализируемом ряду составило 40, что свидетельствует о наличии случайно распределенных во времени колебаний.
Показателями силы колебаний уровней являются: амплитуда отклонений уровней отдельных периодов или моментов от тренда (по модулю), среднее абсолютное отклонение уровней от тренда (по модулю), среднее квадратическое отклонение уровней от тренда, а также относительные меры колеблемости: относительное линейное отклонение от тренда и коэффициент колеблемости.
Особенностью методики вычисления средних отклонений от тренда является необходимость учета потерь степеней свободы колебаний на величину, равную числу параметров уравнения тренда (p).
Учитывая потерю степеней свободы, основные абсолютные показатели колеблемости вычисляются по формулам:
среднее линейное отклонение 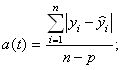 (3)
(3)
среднее квадратическое отклонение 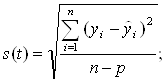 (4)
(4)
коэффициент колеблемости ![]() (5)
(5)
Тренд принимаем по результатам многократного скользящего выравнивания. Амплитуда колебаний составила от 3,6 ц/га в 1954 г. до 20,6 ц/га в 1990 г., т.е.17. Среднее линейное отклонение составляет a (t) =3,88 ц/га. Среднее квадратическое отклонение уровней от тренда составило: s (t) =4,59 ц/га. Коэффициент колеблемости: v (t) =38,7%. Колеблемость урожайности сильная.
Близость фактического распределения временного ряда остатков к нормальному позволяет рассчитать доверительные границы для показателей колеблемости и глубже проанализировать динамику урожайности культур.
Для среднего квадратического
отклонения доверительная граница существования при α=0,05 имеет вид: 4,59 ± 0,19 ц/га (![]() ).
).
Средняя ошибка репрезентативности выборочной оценки для коэффициента колеблемости:
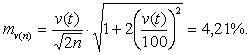 (6)
(6)
Таким образом, доверительный интервал для коэффициента колеблемости равен 38,71 ± 8,45%.
Близость фактических уровней к тренду характеризует показатель устойчивости, который равен разности между единицей и относительным показателем колеблемости: 1-v (t). В нашем случае он равен 61,3 %.
Устойчивость во втором смысле характеризует не сами по себе уровни, а процесс их направленного изменения. В качестве показателя устойчивости тенденции используем коэффициент корреляции рангов Ч. Спирмена ρ. В случае полной устойчивости возрастания уровней коэффициент корреляции рангов равен +1. При полной противоположности рангов уровней рангам лет коэффициент Спирмена равен - 1. При хаотическом чередовании рангов уровней коэффициент близок к нулю, это означает неустойчивость какой-либо тенденции. [2]
Коэффициент корреляции Спирмена по данным о динамике урожайности составил: ρ = 0,448. Положительное значение ρ указывает на наличие тенденции повышения уровней, причем устойчивость этой тенденции средняя.
Методика статистического прогноза по тренду и колеблемости основана, на их экстраполяции, т.е. на предположении, что параметры тренда и колебаний сохраняются до прогнозируемого периода. Осуществим прогнозирование урожайности зерновых культур по тренду с учетом колеблемости. За основу прогнозов возьмем параметры, полученные методом многократного скользящего выравнивания. Параллельно покажем и результаты расчетов при однократном выравнивании.
Вычисляем "точечный прогноз" - значение уровня тренда при подстановке в его уравнение номера 2009 г.:
![]() .
.
Наиболее вероятное значение урожайности зерновых культур Волгоградской области в 2009 г. составит около 14,9 ц/га. Однако параметры тренда, полученные по ограниченному числу уровней ряда, - это лишь выборочные средние оценки, не свободные от влияния распределения колебаний отдельных уровней во времени.
Средние ошибки прогноза положения линейного тренда на год с номером tk рассчитываются по формулам:
для однократного выравнивания:
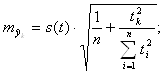 (7)
(7)
для многократного выравнивания:
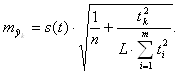 (8)
(8)
В таблице 2 приведены уравнения линейного и параболического
трендов, а также значения скорректированного коэффициента детерминации ![]() и средней ошибки прогноза положения тренде для каждого из них на 2009 г.
и средней ошибки прогноза положения тренде для каждого из них на 2009 г.
Согласно данным табл.2 наиболее высокое значение скорректированного коэффициента детерминации имеет параболический тренд.
Таблица 2 - Средние ошибки прогноза в зависимости от типа тренда
| Тип тренда | Уравнение |
|
Средняя ошибка прогноза |
|
Линейный (однократное выравнивание) |
|
0, 196 | 1,28 |
|
Параболический (однократное выравнивание) |
|
0, 209 | 0,97 |
| Линейный (многократное выравнивание) |
|
0,183 | 0,77 |
Средняя ошибка прогноза для параболического на 27% ниже, чем для линейного тренда при однократном выравнивании. Однако, выравнивание по всем n = 55 уровням несколько завышает значение среднего абсолютного прироста, так как начальный уровень имеет малое значение (4,8), а конечный уровень - большее (13,5). Однократное выравнивание дает величину среднегодового повышения урожайности на 0,139 ц/га.
Избежать преимущественного влияния уровней, стоящих на концах временного ряда, позволяет многократное выравнивание, при котором значение параметра b = 0,105. Следовательно, метод многократного выравнивания на 40% снизил среднюю ошибку прогноза положения линейного тренда.
Предельная ошибка прогноза положения линейного тренда при многократном выравнивании: ∆=m∙tкр=0,77∙2,006=1,54 ц/га. С вероятностью 0,95 можно ожидать, что трендовая компонента величины урожайности в 2009г. составит от 13,4 до16,4 ц/га.
Однако фактические уровни ряда отклоняются от тренда. Уровень урожайности в 2009 г. также может быть не равен трендовому значению. Ошибка прогноза конкретного уровня включает две неопределенности: во-первых, мы не знаем точно, где окажется тренд в 2009 г., а во-вторых, в какую сторону и на сколько уровень ряда отклонится в 2009 г. от его положения. Считая колебания случайно распределенными во времени, т.е. независимыми от тренда, определим ошибку прогноза уровня конкретного года по правилу сложения независимых дисперсий:
![]() (9)
(9)
С вероятностью 0,95 ошибка прогноза уровня урожайности не превзойдет 9,3 ц/га, и доверительные границы прогноза составят от 5,6 до 24,2 ц/га. Как видим, точность прогноза невелика, разброс возможных значений достиг 18,6 ц/га, а вероятная ошибка составила 62 % точечного прогноза.
Итоги прогностических расчетов средней урожайности зерновых в Волгоградской области в 2009-2011 гг. представлены в таблице 3.
Значительная изменчивость v (t) =38,7% уровней урожайности зерновых культур обуславливает необходимость оценки рисков больших отклонений от тренда. При близком к нормальному закону распределении отклонений от тренда вероятность того, что урожайность зерновых культур в 2009 г. окажется в среднем за год ниже 5,6 ц/га, составит 2,5%. Риск того, что отклонение от тренда превысит 3 ц/га равен 25%.
Таблица 3 - Прогноз урожайности зерновых культур Волгоградской области, ц/га
| Годы | "Точечный прогноз" | Доверительные границы прогнозного значения | |||
| линии тренда | урожайности | ||||
| нижняя | верхняя | нижняя | верхняя | ||
| 2009 | 14,9 | 13,4 | 16,4 | 5,57 | 24,25 |
| 2010 | 15 | 13,5 | 16,5 | 5,67 | 24,36 |
| 2011 | 15,1 | 13,6 | 16,6 | 5,77 | 24,47 |
Таким образом, с помощью использованной методики многократного выравнивания, по сравнению с однократным выравниванием, удается уменьшить среднюю ошибку прогноза трендовой компоненты в анализируемом периоде. В то же время отметим, что главной составляющей погрешности прогноза конкретного уровня является не ошибка прогноза положения тренда, а погрешность, обусловленная колеблемостью уровней урожайности относительно тренда. Поэтому суммарная ошибка прогноза конкретного уровня за счет применения многократного выравнивания сократилась в меньшей степени, чем трендовой компоненты.
зерновой урожайность эконометрическое моделирование
Список использованной литературы
1. Гришин, А.Ф. Статистические модели в экономике / А.Ф. Гришин, С.Ф. Котов-Дарти, В.Н. Ягунов. - Ростов н/Д: "Феникс", 2005. - 344 с.
2. Елисеева, И.И. Общая теория статистики: Учебник / И.И. Елисеева, М.М. Юзбашев / Под ред.И. И. Елисеевой. - 5-е изд., перераб. и доп. - М.: Финансы и статистика, 2006. - 656 с.