Дипломная работа: Обобщённо булевы решетки
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
Вятский
государственный гуманитарный университет
Математический факультет
Кафедра алгебры и геометрии
Выпускная квалификационная работа
Обобщенно булевы решетки
Выполнил:
студент V курса математического факультета
Онучин Андрей Владимирович
Научный руководитель:
к.ф.-м.н.,
доцент кафедры алгебры и геометрии ВятГГУ
Чермных Василий Владимирович
Рецензент:
д.ф.-м.н., профессор, зав. кафедрой алгебры и геометрии ВятГГУ
Вечтомов Евгений Михайлович
Работа допущена к защите в государственной аттестационной комиссии
«___» __________2005 г. Зав. кафедрой Е.М. Вечтомов
«___»__________2005 г. Декан факультета В.И. Варанкина
Киров
2005
Содержание
Введение.......................................................................................................... 3
Глава 1............................................................................................................. 4
1.1. Упорядоченные множества................................................................... 4
1.2. Решётки.................................................................................................. 5
1.3. Дистрибутивные решётки..................................................................... 7
1.4. Обобщённые булевы решётки, булевы решётки................................. 8
1.5. Идеалы................................................................................................... 9
Глава 2........................................................................................................... 11
2.1. Конгруэнции....................................................................................... 11
2.2. Основная теорема............................................................................... 16
Библиографический список.......................................................................... 22
Введение
Булева решётка представляет собой классический математический объект, который начал интенсивно изучаться в работах М. Стоуна 30-е годы 20-го века, расширением этого понятия до обобщённо булевых решёток занимались Г. Гретцер и Е. Шмидт в своих трудах конца 50-х годов.
Цель данной работы: установление взаимно однозначного соответствия между конгруэнциями и идеалами в обобщённо булевых решётках. (Для булевых решёток это положение доказано в книге [2], кроме того, сформулировано в книге [3] в качестве упражнений). А также – установление связи между обобщённо булевыми решётками и булевыми кольцами.
Данная дипломная работа состоит из двух глав: в первой главе даны основные понятия, а так же содержатся базовые сведения из теории решёток. Кроме того, в первой главе рассмотрено несколько простейших теорем.
Вторая глава представляет собой основную часть данной дипломной работы. Опираясь на работы Гретцера Г., но более подробно, рассмотрены свойства конгруэнций и связь конгруэнций и идеалов в обобщённо булевых решётках (Теоремы 2.1, 2.2, 2.3.). Кроме того реализована основная цель данной дипломной работы: установлена связь между булевыми кольцами и обобщённо булевыми решётками (Основная теорема).
Глава 1
1.1. Упорядоченные множества
Упорядоченным
множеством P называется непустое множество, на
котором определено бинарное отношение ![]() ,
удовлетворяющее для всех
,
удовлетворяющее для всех ![]() следующим
условиям:
следующим
условиям:
1. Рефлексивность: ![]() .
.
2. Антисимметричность. Если
![]() и
и ![]() , то
, то ![]() .
.
3. Транзитивность. Если ![]() и
и ![]() , то
, то ![]() .
.
Если ![]() и
и ![]() , то говорят, что
, то говорят, что ![]() меньше
меньше ![]() или
или ![]() больше
больше ![]() , и пишут
, и пишут ![]() или
или ![]() .
.
Примеры упорядоченных множеств:
1.
Множество целых положительных чисел, а ![]() означает,
что
означает,
что ![]() делит
делит ![]() .
.
2.
Множество всех
действительных функций ![]() на отрезке
на отрезке ![]() и
и ![]() означает, что
означает, что ![]() для
для ![]() .
.
Цепью называется упорядоченное множество, на котором для
любых ![]() имеет место
имеет место ![]() или
или ![]() .
.
Используя отношение
порядка, можно получить графическое представление любого конечного
упорядоченного множества P.
Изобразим каждый элемент множества P в виде небольшого кружка, располагая x выше y,
если ![]() . Соединим x и y отрезком. Полученная фигура называется диаграммой
упорядоченного множества P.
. Соединим x и y отрезком. Полученная фигура называется диаграммой
упорядоченного множества P.
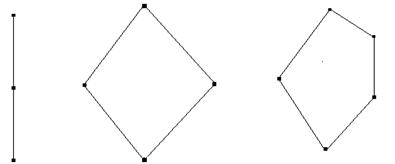 |
Примеры диаграмм упорядоченного множества:
1.2. Решётки
Верхней гранью подмножества Х в упорядоченном множестве Р называется элемент a из Р, больший или равный всех x из X.
Точная верхняя грань подмножества X упорядоченного множества P – это такая его верхняя грань, которая меньше любой другой его верхней грани. Обозначается символом sup X и читается «супремум X».
Согласно аксиоме антисимметричности упорядоченного множества, если точная верхняя грань существует, то она единственна.
Понятия нижней грани и точной нижней грани (которая обозначается inf X и читается «инфинум») определяются двойственно. Также, согласно аксиоме антисимметричности упорядоченного множества, если точная нижняя грань X существует, то она единственна.
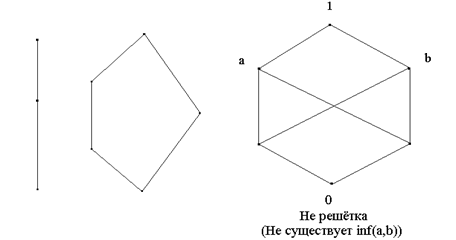 |
Решёткой
Примеры решёток:
Примечание. Любая цепь
является решёткой, т.к. ![]() совпадает
с меньшим, а
совпадает
с меньшим, а ![]() с большим из элементов
с большим из элементов ![]() .
.
Наибольший элемент, то есть элемент, больший или равный каждого элемента упорядоченного множества, обозначают 1, а наименьший элемент, то есть меньший или равный каждого элемента упорядоченного множества, обозначают 0.
На решётке можно рассматривать две бинарные операции:
![]() - сложение и
- сложение и
![]() - произведение
- произведение
Эти операции обладают следующими свойствами:
1. ![]() ,
, ![]() идемпотентность;
идемпотентность;
2. ![]() ,
, ![]() коммутативность;
коммутативность;
3. ![]() ,
, ![]() ассоциативность;
ассоциативность;
4. ![]() ,
, ![]() законы поглощения.
законы поглощения.
ТЕОРЕМА 1.1. Пусть L - множество с двумя бинарными операциями ![]() , обладающими свойствами
(1) – (4). Тогда отношение
, обладающими свойствами
(1) – (4). Тогда отношение ![]() (или
(или ![]() ) является порядком на L, а возникающее упорядоченное
множество оказывается решёткой, причём:
) является порядком на L, а возникающее упорядоченное
множество оказывается решёткой, причём: ![]() и
и
![]() .
.
Доказательство. Рефлексивность отношения ![]() вытекает из свойства (1). Заметим,
что оно является следствием свойства (4):
вытекает из свойства (1). Заметим,
что оно является следствием свойства (4):
![]()
![]()
Если ![]() и
и ![]() , то есть
, то есть ![]() и
и ![]() , то в силу свойства (2),
получим
, то в силу свойства (2),
получим ![]() . Это означает, что
отношение
. Это означает, что
отношение ![]() антисимметрично.
антисимметрично.
Если ![]() и
и ![]() , то применяя свойство (3),
получим:
, то применяя свойство (3),
получим: ![]() , что доказывает
транзитивность отношения
, что доказывает
транзитивность отношения ![]() .
.
Применяя свойства (3), (1), (2), получим:
![]() ,
,
![]() .
.
Следовательно, ![]() и
и ![]() .
.
Если ![]() и
и ![]() , то используя свойства (1)
– (3), имеем:
, то используя свойства (1)
– (3), имеем:
![]() , т.е.
, т.е. ![]() .
.
По определению точней
верхней грани убедимся, что ![]() .
.
Из свойств (2), (4)
вытекает, что ![]() и
и ![]() .
.
Если ![]() и
и ![]() , то по свойствам (3), (4)
получим:
, то по свойствам (3), (4)
получим:
![]() .
.
Отсюда по свойствам (2) и (4) следует, что
![]() .
.
Таким образом, ![]() .
.
Пусть L решётка, тогда её наибольший элемент 1 характеризуется одним из свойств:
1.![]()
![]() .
.
2.![]()
![]() .
.
Аналогично
характеризуется наименьший элемент ![]() :
:
1.![]()
![]()
2.![]()
![]() .
.
1.3. Дистрибутивные решётки
Решётка L называется дистрибутивной,
если для любых ![]() выполняется:
выполняется:
D1. ![]() .
.
D2. ![]() .
.
В любой решётке тождества D1 и D2 равносильны. Доказательство этого факта содержится в книге [2], стр. 24.
Примеры дистрибутивных решёток:
1.
Множество
целых положительных чисел, ![]() означает,
что
означает,
что ![]() делит
делит ![]() . Это решётка с операциями
НОД и НОК.
. Это решётка с операциями
НОД и НОК.
2. Любая цепь является дистрибутивной решёткой.
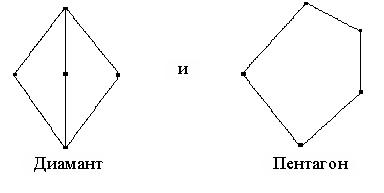 |
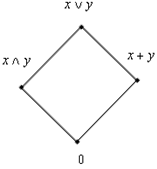
ТЕОРЕМА 1.2. Решётка L с 0 и 1 является дистрибутивной тогда и только тогда, когда она не содержит подрешёток вида
Доказательство этой теоремы можно найти в книге [1].
1.4. Обобщённо булевы решётки, булевы решётки
Всюду далее под словом «решётка» понимается произвольная дистрибутивная решётка с 0.
Решётка L
называется обобщённой булевой, если для любых элементов ![]() и d из L, таких что
и d из L, таких что ![]() существует относительное
дополнение на интервале
существует относительное
дополнение на интервале ![]() , т.е.
такой элемент
, т.е.
такой элемент ![]() из L, что
из L, что ![]() и
и ![]() .
.
(Для ![]() ,
, ![]() , интервал
, интервал ![]() |
|![]() ; для
; для ![]() ,
, ![]() можно так же определить полуоткрытый
интервал
можно так же определить полуоткрытый
интервал ![]() |
|![]() ).
).
ТЕОРЕМА 1.3. (О единственности относительного дополнения в обобщённо булевой решётке). Каждый элемент обобщённо булевой решётки L имеет только одно относительное дополнение на промежутке.
Доказательство. Пусть для элемента ![]() существует два
относительных дополнения
существует два
относительных дополнения ![]() и
и ![]() на интервале
на интервале ![]() . Покажем, что
. Покажем, что ![]() . Так как
. Так как ![]() относительное дополнение
элемента
относительное дополнение
элемента ![]() на промежутке
на промежутке ![]() , то
, то ![]() и
и ![]() , так же
, так же ![]() относительное дополнение
элемента
относительное дополнение
элемента ![]() на промежутке
на промежутке ![]() , то
, то ![]() и
и ![]() .
.
Отсюда
![]()
![]() ,
,
таким образом ![]() , т.е. любой элемент
обобщённой булевой решётки имеет на промежутке только одно относительное
дополнение.
, т.е. любой элемент
обобщённой булевой решётки имеет на промежутке только одно относительное
дополнение.
Решётка L называется
булевой, если для любого элемента ![]() из
L существует дополнение,
т.е. такой элемент
из
L существует дополнение,
т.е. такой элемент ![]() из L, что
из L, что ![]() и
и ![]()
ТЕОРЕМА 1.4. (О единственности дополнения в булевой решётке). Каждый элемент булевой решётки L имеет только одно дополнение.
Доказательство аналогично доказательству теоремы 1.3.
ТЕОРЕМА 1.5. (О связи обобщённо булевых и булевых решёток).
Любая булева решётка является обобщённо булевой, обратное утверждение не верно.
Доказательство. Действительно, рассмотрим
произвольную булеву решётку L. Возьмём элементы a и d из L, такие что ![]() . Заметим, что
относительным дополнением элемента a до элемента d является элемент
. Заметим, что
относительным дополнением элемента a до элемента d является элемент ![]() , где a’ – дополнение элемента a в булевой решётке L. Действительно,
, где a’ – дополнение элемента a в булевой решётке L. Действительно, ![]() , кроме того
, кроме того ![]() . Отсюда следует, что
решётка L является обобщённо булевой.
. Отсюда следует, что
решётка L является обобщённо булевой.
1.5. Идеалы
Подрешётка I решётки L называется идеалом,
если для любых элементов ![]() и
и ![]() элемент
элемент ![]() лежит в I. Идеал I называется собственным,
если
лежит в I. Идеал I называется собственным,
если ![]() . Собственный идеал решётки
L называется простым,
если из того, что
. Собственный идеал решётки
L называется простым,
если из того, что ![]() и
и ![]() следует
следует ![]() или
или ![]() .
.
Так как
непустое пересечение любого числа идеалов снова будет идеалом, то мы можем
определить идеал, порождённый множеством H в решётке L, предполагая, что H не совпадает с пустым
множеством. Идеал, порождённый множеством H будет обозначаться через
(H]. Если ![]() , то вместо
, то вместо ![]() будем писать
будем писать ![]() и называть
и называть ![]() главным идеалом.
главным идеалом.
ТЕОРЕМА
1.5.
Пусть L – решётка, а H и I – непустые подмножества в
L, тогда I является идеалом тогда и
только тогда, когда если ![]() , то
, то ![]() , и если
, и если ![]() , то
, то ![]() .
.
Доказательство.
Пусть I – идеал, тогда ![]() влечёт за собой
влечёт за собой ![]() , так как I – подрешётка. Если
, так как I – подрешётка. Если ![]() , то
, то ![]() и условия теоремы
проверены.
и условия теоремы
проверены.
Обратно,
пусть I удовлетворяет этим условиям и ![]() . Тогда
. Тогда ![]() и так как
и так как ![]() , то
, то ![]() , следовательно, I – подрешётка. Наконец,
если
, следовательно, I – подрешётка. Наконец,
если ![]() и
и ![]() , то
, то ![]() , значит,
, значит, ![]() и I является идеалом.
и I является идеалом.
Глава 2
2.1. Конгруэнции
Отношение
эквивалентности
(т.е. рефлексивное, симметричное и транзитивное бинарное отношение) ![]() на решётке L называется конгруэнцией на L, если
на решётке L называется конгруэнцией на L, если ![]() и
и
![]() совместно влекут за собой
совместно влекут за собой ![]() и
и ![]() (свойство стабильности).
Простейшими примерами являются ω, ι, определённые так:
(свойство стабильности).
Простейшими примерами являются ω, ι, определённые так:
![]() (ω)
(ω)![]()
![]() ;
; ![]() (ι)
для всех
(ι)
для всех ![]() .
.
Для ![]() обозначим через
обозначим через ![]() смежный класс,
содержащий элемент
смежный класс,
содержащий элемент ![]() , т.е.
, т.е. ![]() |
|![]()
Пусть L – произвольная решётка и ![]() . Наименьшую конгруэнцию,
такую, что
. Наименьшую конгруэнцию,
такую, что ![]() для всех
для всех ![]() , обозначим через
, обозначим через ![]() и назовём конгруэнцией,
порождённой множеством
и назовём конгруэнцией,
порождённой множеством ![]() .
.
ЛЕММА 2.1. Конгруэнция ![]() существует для любого
существует для любого ![]() .
.
Доказательство. Действительно, пусть Ф = ![]() |
|![]() для всех
для всех ![]()
![]() . Так как пересечение в
решётке
. Так как пересечение в
решётке ![]() совпадает с
теоретико-множественным пересечением, то
совпадает с
теоретико-множественным пересечением, то ![]() для
всех
для
всех ![]() . Следовательно, Ф=
. Следовательно, Ф=![]() .
.
В двух случаях мы будем
использовать специальные обозначения: если ![]() или
или
![]() и
и ![]() - идеал, то вместо
- идеал, то вместо ![]() мы пишем
мы пишем ![]() или
или ![]() соответственно.
Конгруэнция вида
соответственно.
Конгруэнция вида ![]() называется
главной; её значение объясняется следующей леммой:
называется
главной; её значение объясняется следующей леммой:
ЛЕММА 2.2. ![]() =
=![]() |
|![]() .
.
Доказательство. Пусть ![]() , тогда
, тогда ![]() , отсюда
, отсюда ![]() . С другой стороны
рассмотрим
. С другой стороны
рассмотрим ![]() , но тогда
, но тогда ![]() . Поэтому
. Поэтому ![]() и
и ![]() .
.
Заметим, что ![]() - наименьшая конгруэнция,
относительно которой
- наименьшая конгруэнция,
относительно которой ![]() , тогда как
, тогда как ![]() - наименьшая конгруэнция,
такая, что
- наименьшая конгруэнция,
такая, что![]() содержится в одном смежном классе. Для произвольных
решёток о конгруэнции
содержится в одном смежном классе. Для произвольных
решёток о конгруэнции ![]() почти ничего не
известно. Для дистрибутивных решёток важным является следующее описание
конгруэнции
почти ничего не
известно. Для дистрибутивных решёток важным является следующее описание
конгруэнции ![]() :
:
ТЕОРЕМА 2.1. Пусть ![]() -
дистрибутивная решётка,
-
дистрибутивная решётка, ![]() и
и ![]() . Тогда
. Тогда ![]() и
и ![]() .
.
Доказательство. Обозначим через Ф бинарное
отношение, определённое следующим образом: ![]() и
и
![]() .
.
Покажем, что Ф – отношение эквивалентности:
1) Ф – отношение рефлексивности: x·a = x·a ; x+b = x+b;
2) Ф – отношение симметричности:
![]()
![]() x·a = y·a и x+b = y+b
x·a = y·a и x+b = y+b ![]() y·a = x·a и y+b = x+b
y·a = x·a и y+b = x+b ![]()
![]() ;
;
3) Ф – отношение транзитивности.
Пусть ![]()
![]() x·a = y·a и x+b = y+b и пусть
x·a = y·a и x+b = y+b и пусть ![]()
![]() y·с = z·с и y+d = z+d. Умножим обе части x·a = y·a на элемент с, получим x·a·c = y·a·c. А обе части y·с = z·с умножим на элемент a, получим y·c·a = z·c·a. В силу симметричности x·a·c = y·a·c = z·a·c. Аналогично получаем x+b+d = y+b+d = z+b+d. Таким образом
y·с = z·с и y+d = z+d. Умножим обе части x·a = y·a на элемент с, получим x·a·c = y·a·c. А обе части y·с = z·с умножим на элемент a, получим y·c·a = z·c·a. В силу симметричности x·a·c = y·a·c = z·a·c. Аналогично получаем x+b+d = y+b+d = z+b+d. Таким образом ![]() .
.
Из всего выше обозначенного следует, что Ф – отношение эквивалентности.
Покажем, что Ф
сохраняет операции. Если ![]() и z
и z![]() L, то (x+z) ·a = (x·a) + (z·a) = (y·a) + (z·a) = (y+z) ·a и (x+z)+b = z+(x+b) = z+(y+b); следовательно,
L, то (x+z) ·a = (x·a) + (z·a) = (y·a) + (z·a) = (y+z) ·a и (x+z)+b = z+(x+b) = z+(y+b); следовательно, ![]() .
Аналогично доказывается, что
.
Аналогично доказывается, что ![]() и,
таким образом, Ф – конгруэнция.
и,
таким образом, Ф – конгруэнция.
Наконец, пусть ![]() - произвольная
конгруэнция, такая, что
- произвольная
конгруэнция, такая, что ![]() , и пусть
, и пусть ![]() .
Тогда x·a = y·a, x+b = y+b ,
.
Тогда x·a = y·a, x+b = y+b , ![]() и
и ![]() . Поэтому вычисляя по модулю
. Поэтому вычисляя по модулю ![]() , получим
, получим
![]()
![]()
![]() , т.е.
, т.е. ![]() , и таким образом,
, и таким образом, ![]() .
.
СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ
2.1. Пусть I – произвольный идеал дистрибутивной
решётки L. Тогда ![]() в
том и только том случае, когда
в
том и только том случае, когда ![]() для
некоторого
для
некоторого ![]() . В частности, идеал I является смежным классом по модулю
. В частности, идеал I является смежным классом по модулю ![]() .
.
Доказательство. Если ![]() , то
, то ![]() и элементы x·y·i, i принадлежат идеалу I.
и элементы x·y·i, i принадлежат идеалу I.
Действительно ![]() .
.
Покажем, что ![]() .
.
Воспользуемся тем, что ![]() (*), заметим, что
(*), заметим, что ![]() и
и ![]() , поэтому мы можем
прибавить к тождеству (*)
, поэтому мы можем
прибавить к тождеству (*) ![]() или
или ![]() , и тождество при этом
будет выполняться.
, и тождество при этом
будет выполняться.
![]() Прибавим
Прибавим ![]() :
:
![]() , получим
, получим ![]() .
.
![]() Прибавим
Прибавим ![]() :
:
![]() , получим
, получим ![]() .
.
Отсюда ![]() . Таким образом,
. Таким образом,![]() .
.
Обратно согласно лемме 2,
![]() |
|![]()
Однако ![]() и поэтому
и поэтому ![]() |
|![]()
Если ![]() , то
, то ![]() откуда
откуда
![]() .
.
Действительно, ![]() (**).
(**).
Рассмотрим правую часть этого тождества:
Объединим первое и второе слагаемые –
![]() .
.
Объединим первое и третье слагаемые –
![]() ,
,
таким образом ![]() (***)
(***)
Заметим, что ![]() , поэтому прибавим к обеим
частям выражения (***) y:
, поэтому прибавим к обеим
частям выражения (***) y:
![]()
![]()
Но ![]() , отсюда
, отсюда ![]() .
.
Следовательно, условие
следствия из теоремы 2.1. выполнено для элемента ![]() .
Наконец, если
.
Наконец, если ![]() и
и ![]() , то
, то ![]() , откуда
, откуда ![]() и
и ![]() , т.е.
, т.е. ![]() является смежным классом.
является смежным классом.
ТЕОРЕМА 2.2. Пусть L – булева решётка. Тогда отображение ![]()
![]()
![]() является взаимно
однозначным соответствием между конгруэнциями и идеалами решётки L. (Под
является взаимно
однозначным соответствием между конгруэнциями и идеалами решётки L. (Под ![]()
![]() понимаем класс нуля по
конгруэнции
понимаем класс нуля по
конгруэнции ![]() , под
, под ![]() понимаем решётку
конгруэнций.)
понимаем решётку
конгруэнций.)
 Доказательство. В силу следствия из теоремы 2.1. это
отображение на множество идеалов; таким образом мы должны только доказать, что
оно взаимно однозначно, т.е. что смежный класс
Доказательство. В силу следствия из теоремы 2.1. это
отображение на множество идеалов; таким образом мы должны только доказать, что
оно взаимно однозначно, т.е. что смежный класс ![]() определяет
конгруэнцию
определяет
конгруэнцию ![]() . Это утверждение, однако,
очевидно. Действительно
. Это утверждение, однако,
очевидно. Действительно ![]() тогда и
только тогда, когда
тогда и
только тогда, когда ![]() (*), последнее
сравнение в свою очередь равносильно сравнению
(*), последнее
сравнение в свою очередь равносильно сравнению ![]() ,
где с – относительное дополнение элемента
,
где с – относительное дополнение элемента ![]() в
интервале
в
интервале ![]() .
.
Действительно, помножим выражение (*) на с:
![]() , но
, но![]() ,
а
,
а ![]() , отсюда
, отсюда ![]() .
.
Таким образом, ![]() в том и только том случае,
когда
в том и только том случае,
когда ![]() .
.
Примечание. Приведённое доказательство не полностью использует условие, что L – дистрибутивная решётка с дополнениями. Фактически, мы пользовались только тем, что L имеет нуль и является решёткой с относительными дополнениями. Такая решётка называется обобщённой булевой решёткой.
ТЕОРЕМА 2.3 (Хасимото [1952]). Пусть L – произвольная решётка. Для того,
чтобы существовало взаимно однозначное соответствие между идеалами и
конгруэнциями решётки L,
при котором идеал, соответствующий конгруэнции ![]() ,
являлся бы смежным классом по
,
являлся бы смежным классом по ![]() ,
необходимо и достаточно, чтобы решётка L была обобщённой булевой.
,
необходимо и достаточно, чтобы решётка L была обобщённой булевой.
 Доказательство. Достаточность следует из
доказательства теоремы 2.2. Перейдём к доказательству необходимости.
Доказательство. Достаточность следует из
доказательства теоремы 2.2. Перейдём к доказательству необходимости.
Идеалом, соответствующим
конгруэнции ![]() , должен быть (0]; следовательно,
L имеет нуль 0.
, должен быть (0]; следовательно,
L имеет нуль 0.
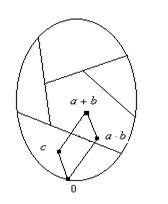
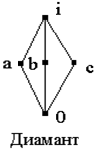
 Если L содержит диамант
Если L содержит диамант ![]() , то идеал (a] не может быть смежным классом, потому что из
, то идеал (a] не может быть смежным классом, потому что из ![]() следует
следует ![]() и
и ![]() . Но
. Но ![]() , значит, любой смежный
класс, содержащий
, значит, любой смежный
класс, содержащий ![]() , содержит и
, содержит и ![]() , и
, и ![]() .
.
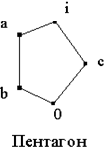
Аналогично, если L содержит пентагон ![]() и смежный класс содержит
идеал
и смежный класс содержит
идеал ![]() , то
, то ![]() и
и ![]() , откуда
, откуда ![]() . Следовательно, этот
смежный класс должен содержать
. Следовательно, этот
смежный класс должен содержать ![]() и
и ![]() .
.
Итак, решётка L не содержит подрешёток, изоморфных ни диаманту, ни пентагону. Поэтому, по теореме 1.2., она дистрибутивна.
Пусть ![]() и
и ![]() . Согласно следствию из
теоремы 2.1., для конгруэнции
. Согласно следствию из
теоремы 2.1., для конгруэнции ![]() идеал
идеал ![]() так же является смежным
классом, следовательно,
так же является смежным
классом, следовательно, ![]() ,
откуда
,
откуда ![]() . Опять применяя следствие
из теоремы 2.1. получим,
. Опять применяя следствие
из теоремы 2.1. получим, ![]() для
некоторого
для
некоторого ![]() . Так как
. Так как ![]() , то
, то ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() о
полу орого ледствие 4 получим, цииодержать , соответствующим конгруэнции
образом мы должны только доказать, ______________ и
о
полу орого ледствие 4 получим, цииодержать , соответствующим конгруэнции
образом мы должны только доказать, ______________ и ![]() , т.е. элемент
, т.е. элемент ![]() является относительным
дополнением элемента
является относительным
дополнением элемента ![]() в интервале
в интервале ![]() .
.
2.2. Основная теорема
(1)
 Пусть
Пусть ![]() -
обобщённая булева решётка. Определим бинарные операции
-
обобщённая булева решётка. Определим бинарные операции ![]() на B, полагая
на B, полагая ![]() и
обозначая через
и
обозначая через ![]() относительное
дополнение элемента
относительное
дополнение элемента ![]() в интервале
в интервале ![]() . Тогда
. Тогда ![]() - булево кольцо, т.е.
(ассоциативное) кольцо, удовлетворяющее тождеству
- булево кольцо, т.е.
(ассоциативное) кольцо, удовлетворяющее тождеству ![]() (а
следовательно и тождествам
(а
следовательно и тождествам ![]() ,
, ![]() ).
).
(2)
Пусть ![]() - булево кольцо. Определим
бинарные операции
- булево кольцо. Определим
бинарные операции ![]() и
и ![]() на
на ![]() , полагая, что
, полагая, что ![]() и
и ![]() . Тогда
. Тогда ![]() - обобщённая булева
решётка.
- обобщённая булева
решётка.
Доказательство.
(1)
Покажем, что ![]() - кольцо.
- кольцо.
Напомним определение. Кольцо ![]() - это
непустое множество
- это
непустое множество ![]() с заданными на
нём двумя бинарными операциями
с заданными на
нём двумя бинарными операциями ![]() ,
которые удовлетворяют следующим аксиомам:
,
которые удовлетворяют следующим аксиомам:
1. Коммутативность сложения:
![]() выполняется
выполняется ![]() ;
;
2. Ассоциативность сложения:
![]() выполняется
выполняется ![]() ;
;
3. Существование нуля, т.е. ![]() ,
, ![]() ;
;
4. Существование
противоположного элемента, т.е. ![]() ,
, ![]() ,
, ![]() ;
;
5. Ассоциативность
умножения: ![]() ,
, ![]() ;
;
6. Закон дистрибутивности.
Проверим, выполняются ли аксиомы кольца:
1. Относительным
дополнением до ![]() элемента
элемента ![]() будет элемент
будет элемент ![]() , а относительным
дополнением
, а относительным
дополнением ![]() элемент
элемент ![]()
![]() .
В силу того, что
.
В силу того, что ![]() , а так же
единственности дополнения имеем
, а так же
единственности дополнения имеем ![]() .
.
2. Покажем, что ![]() .
.
 Рассмотрим все возможные
группы вариантов:
Рассмотрим все возможные
группы вариантов:
1) Пусть ![]() , тогда
, тогда ![]() (Далее везде под элементом
x будем понимать сумму
(Далее везде под элементом
x будем понимать сумму ![]() ).
).
Аналогично получаем ![]() в случаях
в случаях ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() . Заметим, что когда один
из элементов равен нулю (например, c),
то получаем тривиальные варианты (a+b=a+b).
. Заметим, что когда один
из элементов равен нулю (например, c),
то получаем тривиальные варианты (a+b=a+b).
2) Пусть ![]() , а элемент c не сравним с ними. Возможны
следующие варианты:
, а элемент c не сравним с ними. Возможны
следующие варианты:
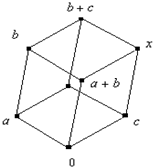
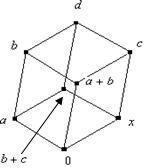
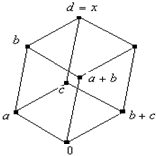
Нетрудно заметить, что во
всех этих случаях ![]() , кроме того:
, кроме того:
если c=a+b, то (a+b)+c=0=a+(b+c);
если c=0, то получаем тривиальный вариант.
Вариант, когда c равен наибольшему элементу решётки d, мы уже рассматривали.
Если c=b, то (a+b)+c=(a+b)+b=a и a+(b+c)=a+(b+b)=a.
Если c=a, то (a+b)+c=(a+b)+a=b и a+(b+c)=a+(b+a)=b.
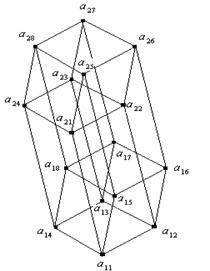 Аналогично
для случаев
Аналогично
для случаев ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
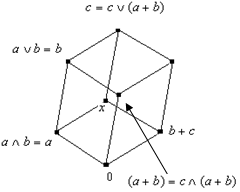
3) Под элементами нижнего
уровня будем понимать элементы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , т.е. те элементы 4-х
мерного куба, которые образуют нижний трёхмерный куб.
, т.е. те элементы 4-х
мерного куба, которые образуют нижний трёхмерный куб.
Под элементами верхнего
уровня будем понимать элементы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , т.е. те элементы 4-х
мерного куба, которые образуют верхний трёхмерный куб.
, т.е. те элементы 4-х
мерного куба, которые образуют верхний трёхмерный куб.
Под фразой «элемент
верхнего уровня, полученный из элемента ![]() нижнего
уровня сдвигом по соответствующему ребру» будем понимать элемент
нижнего
уровня сдвигом по соответствующему ребру» будем понимать элемент ![]() верхнего уровня.
верхнего уровня.
Пусть a, b, c несравнимы. Рассмотрим следующие варианты: ![]() и
и ![]() .
.
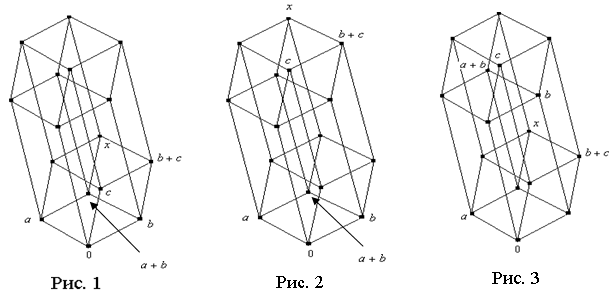 Пусть
Пусть ![]() .
Заметим, что это возможно только в случаях, когда
.
Заметим, что это возможно только в случаях, когда ![]() принадлежат
нижнему уровню, причём лежат на позициях элементов
принадлежат
нижнему уровню, причём лежат на позициях элементов ![]() (рис.
1). Либо a, b остаются на своих позициях, элемент c сдвигается на верхний уровень по
соответствующему ребру (рис. 2). Либо элемент a остаётся на своей позиции, элементы b, c сдвигаются на верхний уровень по соответствующему
ребру (рис 3).
(рис.
1). Либо a, b остаются на своих позициях, элемент c сдвигается на верхний уровень по
соответствующему ребру (рис. 2). Либо элемент a остаётся на своей позиции, элементы b, c сдвигаются на верхний уровень по соответствующему
ребру (рис 3).
 Нетрудно
заметить, что во всех этих случаях
Нетрудно
заметить, что во всех этих случаях ![]() .
.
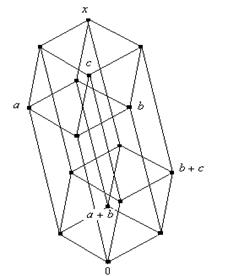
Пусть ![]() , здесь так же
, здесь так же ![]() .
.
Таким образом мы рассмотрели все основные группы вариантов расположения элементов a, b, c и во всех этих случаях ассоциативность сложения выполняется.
3. Рассмотрим в решётке
элемент ![]() , к нему существует
относительное дополнение
, к нему существует
относительное дополнение ![]() до
элемента
до
элемента ![]() , т.е.
, т.е. ![]() и
и ![]() . Учитывая, что в решётке
. Учитывая, что в решётке ![]() и
и ![]() , имеем следующее:
, имеем следующее: ![]() и
и ![]() . Отсюда
. Отсюда ![]() .
.
4. Рассмотрим
относительное дополнение элемента ![]() до
до ![]() , это элемент
, это элемент ![]() . Таким образом:
. Таким образом: ![]() и
и ![]() . Учитывая, что в решётке
выполняются тождества
. Учитывая, что в решётке
выполняются тождества ![]() и
и ![]() имеем следующее:
имеем следующее: ![]() и
и ![]() . Отсюда
. Отсюда ![]() .
.
5. Так как в решётке
выполняется ассоциативность ![]() , а так
же имея
, а так
же имея ![]() , то
, то ![]() .
.
6. Докажем
дистрибутивность ![]() или что то же
самое
или что то же
самое
![]() (*).
(*).
Докажем, что дополнения
левой и правой частей выражения (*) до верхней грани ![]() совпадают.
совпадают.
Нетрудно заметить, что
дополнением правой части выражения (*) до элемента ![]() будет
являться элемент
будет
являться элемент ![]() .
.
Покажем это:
![]() , по определению относительного
дополнения элемента
, по определению относительного
дополнения элемента ![]() (
(![]() ), где за
), где за ![]() приняли элемент
приняли элемент ![]() , а элемент
, а элемент ![]() за
за ![]() .
.
![]() , по определению относительного
дополнения элемента
, по определению относительного
дополнения элемента ![]() (
(![]() ) , где за
) , где за ![]() приняли элемент
приняли элемент ![]() , а элемент
, а элемент ![]() за
за ![]() .
.
Покажем, что и для левой
части (*) элемент ![]() будет являться
относительным дополнением до верхней грани
будет являться
относительным дополнением до верхней грани ![]() :
:
![]() , т.к.
, т.к. ![]() .
.
![]()
Мы показали, что
дополнения элементов ![]() и
и ![]() до верхней грани
до верхней грани ![]() совпадают, следовательно,
в силу единственности дополнения
совпадают, следовательно,
в силу единственности дополнения ![]() . А
значит и
. А
значит и ![]() , т.е. дистрибутивность
доказана.
, т.е. дистрибутивность
доказана.
Таким образом, для ![]() все аксиомы кольца
выполняются.
все аксиомы кольца
выполняются.
Заметим, что ![]() выполняется в силу того,
что
выполняется в силу того,
что ![]() , а в решётке
, а в решётке ![]() .
.
Также выполняется ![]() , потому что
, потому что ![]() .
.
Таким образом, ![]() - булево кольцо.
- булево кольцо.
Доказательство (2). Частичную
упорядоченность ![]() имеем исходя из
того, что исходное булево кольцо
имеем исходя из
того, что исходное булево кольцо ![]() -
частично упорядоченное множество. Кроме того
-
частично упорядоченное множество. Кроме того ![]() -
решётка, т.к.
-
решётка, т.к. ![]() существуют sup(x,y) и inf(x,y), заданные соответствующими правилами:
существуют sup(x,y) и inf(x,y), заданные соответствующими правилами: ![]() и
и ![]() .
.
Покажем, что решётка
дистрибутивна, т.е. что выполняется тождество ![]() (*)
(*)
Рассмотрим левую часть выражения (*):
![]() .
.
Рассмотрим правую часть выражения (*):
![]() ,
,
т.о. тождество ![]() верно, т.е. решётка
верно, т.е. решётка ![]() является дистрибутивной.
является дистрибутивной.
Покажем, что у каждого
элемента ![]() в дистрибутивной решётке
в дистрибутивной решётке ![]() есть относительное
дополнение. Для этого рассмотрим произвольные элементы
есть относительное
дополнение. Для этого рассмотрим произвольные элементы ![]() , но они так же должны
являться элементами решётки
, но они так же должны
являться элементами решётки ![]() ,
следовательно, в ней должны лежать и
,
следовательно, в ней должны лежать и ![]() ,
которым в кольце соответствуют
,
которым в кольце соответствуют ![]() .
.
Рассмотрим элемент булева
кольца ![]() (в решётке лежит
соответствующий ему элемент), заметим, что
(в решётке лежит
соответствующий ему элемент), заметим, что
![]()
и ![]() .
.
Поэтому элемент ![]() будет являться в
дистрибутивной решётке
будет являться в
дистрибутивной решётке ![]() относительным
дополнением
относительным
дополнением ![]() до верхней грани
до верхней грани ![]() .
.
Таким образом, ![]() будет являться
дистрибутивной решёткой с относительными дополнениями (обобщённой булевой).
будет являться
дистрибутивной решёткой с относительными дополнениями (обобщённой булевой).
Библиографический список
1. Гретцер, Г. Общая теория решёток [Текст] / Г. Гретцер. – М.: Мир, 1982.
2. Биркгоф, Г. Теория решёток [Текст] / Г. Биркгоф. – М.: Наука, 1984.
3. Скорняков, Л.А. Элементы алгебры [Текст] / Л.А. Скорняков. – М.: Наука, 1989.