Контрольная работа: Определение интегралов
Задание. Найти неопределенные интегралы. Результат проверить дифференцированием.
а)

Используемый прием интегрирования называется подведением под знак дифференциала. Проверим результат дифференцированием.

б)
В этом интеграле также используется подведение под знак дифференциала
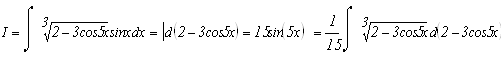
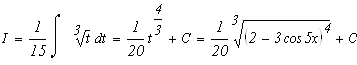
Проверим результат дифференцированием.
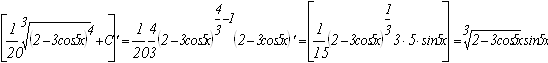
в)
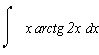
Для решения этого интеграла воспользуемся формулой интегрирования "по частям". Приведем формулу интегрирования по частям:
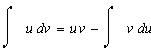
В этом интеграле распишем составляющие следующим образом:
![]()
![]()
Продифференцируем u и проинтегрируем dv чтобы мы могли применить формулу интегрирования по частям:

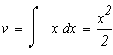
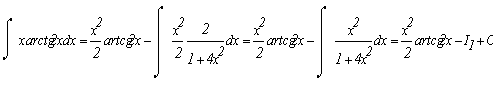
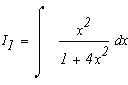
Подинтегральное выражение есть неправильная рациональная дробь. Необходимо привести ее к сумме правильных рациональных дробей, выполнив деление углом числитель на знаменатель.
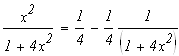

Вернемся к исходному интегралу:
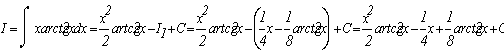
Проверим результат дифференцированием:
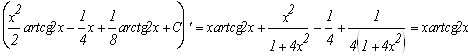

г)
интеграл дифференцирование уравнение парабола
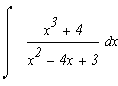
Подинтегральное выражение является неправильной рациональной дробью. Необходимо преобразовать ее в сумму правильных рациональных дробей, выполнив деление углом числитель на знаменатель:
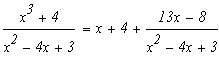
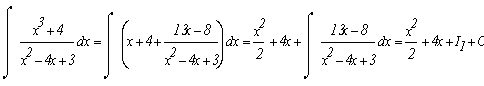

Подинтегральное выражение представляет собой правильную рациональную дробь. Чтобы проинтегрировать её необходимо её представить в виде суммы простейших дробей. Найдем корни знаменателя
![]()
по теореме Виета
![]()
![]()
![]()
Разложим правильную рациональную дробь в сумму простейших методом неопределенных коэффициентов:

Приравнивая коэффициенты при одинаковых степенях х, составим систему линейных алгебраических уравнений для определения неизвестных коэффициентов А и В:
![]()
![]()
![]()
Решая СЛАУ находим значения коэффициентов:
![]()
![]()
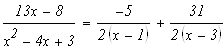

Возвратимся к исходному интегралу:
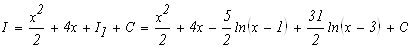
Результат проверим дифференцированием:
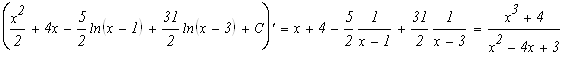
Задание. Вычислить по формуле Ньютона-Лейбница определенный интеграл.
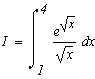
Перейдем к замене переменных в определенном интеграле:
![]()
![]()
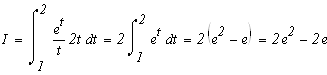
Задание.
Вычислить площадь фигуры, ограниченной параболой ![]() и прямой
и прямой ![]() . Сделать чертеж.
. Сделать чертеж.
Решение.
Площадь области S, ограниченной снизу функцией g(x), сверху- функцией f(x),
слева - вертикальной прямой ![]() , справа - вертикальной прямой
равна
, справа - вертикальной прямой
равна ![]() равна
определенному интегралу:
равна
определенному интегралу:
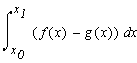
Так
как мы пока не знаем, какая же из функций является большей на отрезке ![]() , построим
чертеж. Точки
, построим
чертеж. Точки ![]() ,
, ![]() являются абсциссами точек
пересечения графиков этих двух функций.
являются абсциссами точек
пересечения графиков этих двух функций.

Как видно из построения парабола лежит выше прямой на отрезке, поэтому:
![]()
![]()
Абсциссы точек пересечения суть соответственно -6 и -1. Эти значения мы также можем получить решив в системе уравнения двух кривых
![]()
![]()
![]()
![]()
![]()
по
теореме Виета имеем: ![]() ,
, ![]() . Теперь осталось только применить
формулу вычисления площади криволинейной области:
. Теперь осталось только применить
формулу вычисления площади криволинейной области:

|
|

Найти
общее решение дифференциального уравнения ![]() и частное решение,
удовлетворяющее начальному условию
и частное решение,
удовлетворяющее начальному условию ![]() при
при ![]()
![]()
Решение:
имеем линейное уравнение первого порядка. будем искать решение уравнения в виде
произведения двух функций от х: ![]()
Запишем исходное выражение в виде:
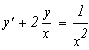
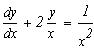
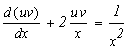
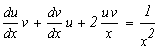
![]()
Выберем
функцию ![]() такой
чтобы выражение в скобках равнялось нулю:
такой
чтобы выражение в скобках равнялось нулю:
![]()
Разделяя переменные в этом дифференциальном уравнении относительно функции v, находим:
![]()
![]()
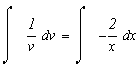
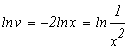
![]()
Так
как выражение в скобках подобрано так, чтобы оно равнялось нулю, подставим
найденное значение ![]() в уравнение
в уравнение 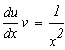 для определения u.
для определения u.
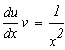
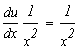
![]()
![]()
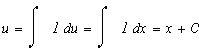
Таким образом находим общее решение системы
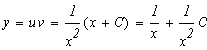
Подберем
переменную С так чтобы выполнились начальные условия ![]() , что будет являться частным
решением дифференциального уравнения:
, что будет являться частным
решением дифференциального уравнения:
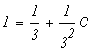
![]()
Полученное частное решение дифференциального уравнения, соответствующее поставленным начальным условиям.
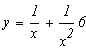
Задание.
Найти общее решение дифференциального уравнения ![]() и частное решение,
удовлетворяющее начальным условиям
и частное решение,
удовлетворяющее начальным условиям ![]() ,
, ![]() при
при ![]() . (
. (![]() ,
,![]() )
)
Решение: Пусть имеем неоднородное линейное уравнение второго порядка:
![]()
Структура общего решения такого уравнения определяется следующей теоремой:
Теорема: Общее решение неоднородного уравнения представляется как сумма какого-нибудь частного решения этого уравнения y* и общего уравнения y соответствующего однородного уравнения:
![]()
Чтобы найти общее решение соответствующего однородного уравнения (то есть такого, в котором правая часть равна нулю) необходимо найти корни характеристического уравнения и по ним определить вид решения.
Характеристическое уравнение в нашем случае есть:
![]()
имеет
действительные и различные корни: ![]() ,
, ![]() .
.
Общий
интеграл есть: ![]()
Правая
часть линейного уравнения второго порядка имеет вид: ![]() , где
, где ![]() - многочлен
0-й степени, =2 (не является корнем
характеристического многочлена).
- многочлен
0-й степени, =2 (не является корнем
характеристического многочлена).
поэтому частное решение следует искать в виде:
![]()
где
![]() -
постоянный коэффициент, подлежащий определению. Подставляя y* в заданное
уравнение, будем иметь:
-
постоянный коэффициент, подлежащий определению. Подставляя y* в заданное
уравнение, будем иметь:
![]()
![]()
![]()
![]()
Имеем решение . Итак, частное решение нашли в виде:
![]()
Таким образом, общий интеграл данного уравнения имеет вид:
![]()
Для определения коэффициентов С1 и С2 используем начальные условия:
При х=0 функция равна 2
![]()
![]()
При х=0 первая производная функции равна -1:
![]()
![]()
Составим систему из этих двух уравнений и решим её относительно неизвестных С1 и С2
![]()
![]()
![]()
![]()
![]()
Таким образом, частное решение данного дифференциального уравнения запишется в виде:
![]()
![]()
![]()
| Большая коллекция шпор для МАТАНа (1 семестр 1 курс) | |
|
1. Векторы. Действия над векторами. Вектором наз. упорядоченная совокупность чисел Х={X1,X2,...Xn} вектор дан в n-мерном пространстве. Т(X1,X2,X3). n ... Рациональная дробь наз. правильной если степень числителя меньше степени знаменателя, т.е. m 5. Дифференцирование неявных функций Пусть уравнение определяет как неявную функцию от х. а) продифференцируем по х обе части уравнения , получим уравнение первой степени ... |
Раздел: Рефераты по математике Тип: шпаргалка |
| Содержание и значение математической символики | |
|
Курсовая работа Выполнила студентка факультета математики 4 курс 4 группа Клочанова Ольга Михайловна Российский государственный педагогический ... Кроме формул, представляющих собой обращение упомянутых формул дифференцирования, Лейбниц дал две работы об интегрировании рациональных дробей (1701 и 1703 гг.) Существенно то, что Лейбниц отчетливо определил взаимоотношение интегрирования дифференциальных уравнений и интегрирования функций (первое следует считать выполненным, если оно ... |
Раздел: Рефераты по математике Тип: дипломная работа |
| Управление сложными системами | |
|
Лекция №1. 11.02.2003 Раздел 1. Основные понятия теории сложности 1.1. Сложность Сложность - свойство современных систем управления. Различают ... Применяя к уравнению (X) пункта № 4.1.1.2.2 преобразование Лапласа при нулевых начальных условиях, с учётом свойств линейности и дифференцирования получим: Из теории дифференциальных уравнений известно, что решение уравнения (5) при известных начальных условиях может быть получено в следующем виде: |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Вклад Л.Эйлера в развитие математического анализа | |
|
План Введение 1 Понятие математического анализа. Исторический очерк 2 Вклад Л.Эйлера в развитие математического анализа 3 Дальнейшее развитие ... При этом элементы функционального анализа и теории интеграла Лебега даются факультативно, а ТФКП, вариационное исчисление, теория дифференциальных уравнений читаются отдельными ... Он продвинул его обоснование, существенно развил интегральное исчисление, методы интегрирования обыкновенных дифференциальных уравнений и уравнений в частных производных. |
Раздел: Рефераты по математике Тип: реферат |
| Методы решения уравнений, содержащих параметр | |
|
Выпускная квалификационная работа Выполнил тудент V курса математического факультета Кузнецов Е.М. Вятский государственный гуманитарный университет ... Имеются задачи (№№971, 972) на применение обратного утверждения теоремы Виета, говорящее о том, что сумма и произведение корней уравнения равны коэффициентам этого уравнения. Процесс решения дробно-рациональных уравнений протекает по обычной схеме: данное уравнение заменяется целым путем умножения обеих частей уравнения на общий знаменатель левой и ... |
Раздел: Рефераты по математике Тип: курсовая работа |