Курсовая работа: Статистические методы анализа результатов деятельности коммерческих банков
КУРСОВАЯ РАБОТА
По дисциплине: «Статистика»
на тему
«Статистические методы анализа результатов деятельности коммерческих банков»
Оглавление
Введение
1. Статистические методы анализа результатов деятельности коммерческих банков
1.1 Основные направления и показатели статистики кредита
1.2 Показатели статистики денежных вкладов, их динамика
1.3 Математическое дисконтирование и банковский учёт
2. Расчетная часть
3. Анализ некоторых аспектов деятельности Сберегательного банка РФ за 2006-2007 гг.
Заключение
Список использованной литературы
Приложения
Введение
В современном обществе статистика как наука выполняет важную роль в механизме управления экономикой. С помощью статистических методов осуществляется сбор, обработка, обобщение и анализ экономической информации, характеризующей развитие страны, культуры и уровня жизни населения. Все это позволяет выявить взаимосвязи между изучаемыми явлениями, определить тенденцию развития, сопоставить и сравнить с международной ситуацией и, в конечном счете, принять эффективные управленческие решения на уровне предприятия, региона или всей страны.
С переходом к рыночной экономике значение статистики возросло, появилась необходимость приведения её в соответствие с международными стандартами. Кроме того, важнейшим направлением развития статистики в последнее время стала разработка методологии и организации получения информации о теневой экономике, результаты деятельности которой скрываются от статистических органов.
Свою роль в процессе сбора и анализа информации статистика играет и в банковской сфере, которая интенсивно развивается с появлением новых видов банковских продуктов. В связи с ростом популярности кредитов в нашей стране развивается статистика кредита.
В данной работе будут рассмотрены основные показатели деятельности коммерческих банков и статистические методы их изучения.
Целью выполнения работы является изучение методики проведения статистических расчётов и формирование выводов на их основе.
1. Статистические методы анализа результатов деятельности коммерческих банков
1.1 Основные направления и показатели статистики кредита
Кредит – это предоставление финансовых ресурсов одним хозяйствующим субъектом другому на условиях срочности, платности и возвратности. Видами кредита в РФ являются:
- государственный кредит (средства, привлеченные государством в виде займов, эмиссии ценных бумаг);
- банковский кредит (выдаваемый банками предприятиям и физическим лицам);
- межбанковский кредит (размещения банками друг у друга денежных средств в форме депозитов и на короткие сроки).
Ссудный капитал образуют временно свободные, высвобожденные в процессе кругооборота денежные средства государства, физических и юридических лиц, переданные на добровольной основе для капитализации и извлечения прибыли. Кредиты различаются по срочности (краткосрочный, среднесрочный, долгосрочный) и по обеспеченности (необеспеченные и под залог векселей, товарных документов, ценных бумаг, недвижимости, страхование ответственности).
К наиболее важным показателям банковского кредита следует отнести:
- общий размер кредитования банками отраслей экономики и населения;
- доля краткосрочного и доля долгосрочного кредитования в общей сумме кредитов;
- просроченная задолженность по ссудам банков;
- процент за кредит и ставка рефинансирования.
Для обобщения и сравнения используются средние величины:
1. Средний размер кредита
Р¯= 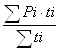 ,
,
где Рi – размер i–й ссуды, ti – срок i–й ссуды.
2. Средний срок пользования кредитами
t¯ = 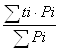
3. Среднее число оборотов ссуд за год
n¯= 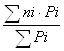 или n¯=
или n¯= ![]()
4. Средняя процентная годовая ставка кредита (i¯):
i¯= 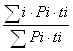
Большое внимание в статистике уделяется показателям долгосрочных ссуд: остаткам задолженности, суммам выданных ссуд, их составу и динамике.
Самостоятельным объектом в статистике кредита является изучение просроченных ссуд по их объёму, составу и динамике. По состоянию на конец года определяют по банку в целом:
1. Абсолютную сумму просроченных кредитов (остатков задолженности)
Рпр = ∑ Рiпр
Относительные показатели просроченной задолженности по ссудам:
а) по сумме Кпр(р) = 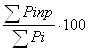 ;
;
б) по сроку Кпр(t) = 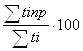 ,
,
где tiпр – число просроченных дней по погашению i-го кредита;
в) по сумме и сроку Кпр =  .
.
Выявление статистических закономерностей в поведении ссудной задолженности является важным средством улучшения уровня управления кредитными ресурсами [1, с. 382-393].
1.2 Показатели статистики денежных вкладов, их динамика
Сбережения и временно свободные денежные средства населения привлекаются сберегательными кредитными учреждениями на выгодное хранение. В сбережениях заинтересованы как банки, так и физические лица, поэтому в банковской системе сберегательное дело занимает особое место. По состоянию на конец 2007 года при численности населения республики Башкортостан 4 млн. человек в Сберегательном банке РФ обслуживаются 6 миллионов счетов клиентов, он по-прежнему остаётся лидером по привлечению средств населения, более половины всех вложений[1]. Основная задача банка обеспечить эффективное перераспределение этих временно свободных финансовых средств между экономическими агентами, это определяет необходимость проведения статистического анализа вкладов населения.
К числу основных показателей денежных вкладов относятся: средний размер вклада, оборачиваемость вкладного рубля, эффективность вкладных операций. Средний размер вклада характеризует достигнутый уровень сбережений, который формируется под влиянием множества факторов: уровня жизни населения, изменения покупательной способности денег, степени удовлетворения предметами потребления, уровня цен на товары и услуги, склонности населения к сбережениям и т.д.
1. Средний размер вклада
l¯= ![]() или l¯ =
или l¯ = 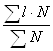
где В – сумма вкладов, N – количество вкладов.
2. Средний срок хранения вкладов
t¯= B¯: ![]() ,
,
где В¯- средний остаток вкладов, Ов – сумма выданных вкладов за период Д, Д – число календарных дней в периоде.
3. Число оборотов
n = ![]()
![]()
Данный показатель показывает, сколько раз обернулись денежные средства во вкладах за определенный период, чем больше оборотов совершают средства, тем эффективнее они используются [1, с. 401-403].
1.3 Математическое дисконтирование и банковский учёт
статистика кредит банковский дисконтирование
В финансово-кредитных расчётах важную роль играет фактор времени. Это объясняется принципом «неравноценности» денег на разные временные даты. В связи с этим нельзя суммировать деньги на разные моменты времени.
Для сопоставимости денег, относящихся к разным датам, прибегают к дисконтированию, т.е. приведению к заданному моменту времени. Дисконтирование применяется, например, при покупке банком краткосрочных финансовых обязательств (векселей, тратт), оплата которых производится в будущем. В зависимости от вида процентной ставки различают два метода дисконтирования: математическое дисконтирование и банковский (коммерческий) учёт. В первом случае используется ставка наращения, во втором – учётная ставка [1, c.446].
При математическом дисконтировании современная капитализированная величина суммы S определяется из уравнения:
S = P·(1+ni),
P = S·![]() или P = S·(1+ni)ˉ¹,
или P = S·(1+ni)ˉ¹,
где ![]() - дисконтный множитель, который показывает, какую долю
составляет первоначальная величина долга Р в окончательной сумме S.
- дисконтный множитель, который показывает, какую долю
составляет первоначальная величина долга Р в окончательной сумме S.
Заметим, что дисконт по соглашению сторон может быть установлен и в виде абсолютной величины для всего срока (без расчёта по формуле).
Суть операции учёта векселя заключается в том, что банк или другое финансовое учреждение до наступления срока платежа по векселю или иному платёжному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает его с дисконтом (со скидкой), получив при наступлении срока векселя деньги, банк реализует дисконт. Владелец векселя с помощью его учёта имеет возможность получить деньги, хотя не в полном объёме, однако раньше указанного срока.
Таким образом, сумма, выплачиваемая при учёте векселя, будет равна:
Р = S –Snd = S·(1-nd),
где n – срок от момента учёта до даты погашения векселя, (1-nd) – дисконтный множитель.
Отсюда срок ссуды равен
n = ![]() ,
,
а величина учётной ставки
d = ![]() .
.
Операция дисконтирования по учётной ставке и начисления простых процентов могут совмещаться. Тогда сумма при учёте обязательства с начислением простых процентов равна
Р2 = Р1(1+n1i)(1-n2d),
где Р1 – первоначальная сумма ссуды,
n1 – срок начисления процентов,
n2 – срок от момента учёта обязательства до даты погашения долга, n1<n2. Простая учётная ставка применяется также, когда необходимо определить сумму, на которую выписывается вексель, если задана текущая стоимость долга.
S = P ·![]() .
.
Процесс дисконтирования по сложной учётной ставке происходит с замедлением, т.к. на каждом этапе во времени учётная ставка применяется не к первоначальной сумме (как при учёте по простой учётной ставке), а к сумме, меньшей на величину дисконта, определенного на предыдущем шаге.
P = S(1-dc)ⁿ,
где dc – сложная годовая учётная ставка.
В рассматриваемых методах наращения все денежные величины применялись по номиналу, т.е. не принималась во внимание реальная покупательная способность денег. Вместе с тем инфляция в современной экономике стала неотъемлемым элементом экономического развития, поэтому её, конечно, необходимо учитывать при проведении финансовых расчётов.
Изменение покупательной способности денег характеризуется с помощью индекса покупательной способности денег (рубля) I n.c.p . Этот индекс равен обратной величине индекса цен. Тогда реальная наращенная сумма денег с учётом её обесценивания будет равна:
С = S·I n.c.p .
Итак, при анализе деятельности коммерческих банков применяются следующие показатели: ряды динамики, абсолютные, относительные и средние величины, индексы, элементы корреляционно-регрессионного анализа; используются методы сводки, группировки; конечные результаты исследования представляются с помощью различных статистических графиков (диаграммы, картограммы). Источником информации может быть публикуемая отчётность банка, как годовая, так и периодическая. Основным видом статистического наблюдения является выборочное, т.к. оно позволяет оценить всю генеральную совокупность при анализе лишь её части.
2. Расчетная часть
Имеются следующие выборочные данные о деятельности российских коммерческих банков с ценными бумагами (выборка 3%-ная механическая), млн. руб.:
| № банка п/п | Вложения в ценные бумаги | Прибыль | № банка п/п | Вложения в ценные бумаги | Прибыль |
| 1 | 4069 | 110 | 19 | 9087 | 439 |
| 2 | 4279 | 538 | 20 | 8016 | 441 |
| 3 | 3959 | 85 | 21 | 7324 | 237 |
| 4 | 1032 | 60 | 22 | 3445 | 282 |
| 5 | 4152 | 39 | 23 | 2079 | 191 |
| 6 | 5347 | 153 | 24 | 2058 | 201 |
| 7 | 2286 | 215 | 25 | 648 | 12 |
| 8 | 2948 | 224 | 26 | 2673 | 77 |
| 9 | 2914 | 203 | 27 | 3145 | 282 |
| 10 | 1600 | 64 | 28 | 2048 | 451 |
| 11 | 2145 | 11 | 29 | 287 | 50 |
| 12 | 3811 | 153 | 30 | 2571 | 306 |
| 13 | 889 | 121 | 31 | 2081 | 440 |
| 14 | 584 | 94 | 32 | 3787 | 204 |
| 15 | 990 | 105 | 33 | 2131 | 63 |
| 16 | 1618 | 93 | 34 | 7298 | 650 |
| 17 | 1306 | 329 | 35 | 4729 | 538 |
| 18 | 1981 | 451 | 36 | 7096 | 175 |
Задание 1
Признак – вложения в ценные бумаги.
Число групп – пять.
Решение.
Построим статистический ряд распределения по признаку – вложения в ценные бумаги, образовав 5 групп с равными интервалами. Для этого определим величину интервала:
i = (9087-287)/5=1760.
Таким образом, получены следующие интервалы:
1) 287+1760=2047;
2) 2047+1760=3807;
3) 3807+1760=5567;
4) 5567+1760=7327;
5) 7327+1760=9087.
Составим расчётную таблицу.
Таблица 1 – Группировка банков по вложениям в ценные бумаги
| № | Интервал | число банков в группе (f) | Середина интервала (x) | x·f | (x-x¯)² | (x-x¯)²·f |
| 1 | 287-2047 | 10 | 1167 | 11670 | 4840000 | 48400000 |
| 2 | 2047-3807 | 14 | 2927 | 40978 | 193600 | 2710400 |
| 3 | 3807-5567 | 7 | 4687 | 32809 | 1742400 | 12196800 |
| 4 | 5567-7327 | 3 | 6447 | 19341 | 9486400 | 28459200 |
| 5 | 7327-9087 | 2 | 8207 | 16414 | 23425600 | 46851200 |
| итого | - | 36 | - | 121212 | 39688000 | 138617600 |
Рассчитаем средние значения x:
1) для несгруппированных данных x¯= 116413/36=3233,6944 (млн.руб);
2) для сгруппированных данных x¯= 121212/36=3367 (млн.руб).
Рассчитаем дисперсию:
σ² = 39688000/36=1102444,4.
Рассчитаем среднее квадратическое отклонение:
σ = (σ²)¹/²= 1049,9735, т.е. отклонение коммерческих банков по признаку вложений в ценные бумаги от среднего значения составляет 1049,9735 млн.руб.
Рассчитаем коэффициент вариации:
ν = σ / x¯ = 1049,9735/3367= 0,3118 или 31,18%, значение коэффициента показывает, что совокупность неоднородная, связь слабая, заметная.
Рассчитаем значения моды и медианны:
2047-3807 - модальный интервал, т.к. он имеет наибольшую частоту f=14.
Мо = 2047+1760·[(14-10)/((14-10)·(14-7))]=2298,4284.
2047-3807 – медианный интервал, т.к. его кумулятивная частота больше половины суммы частот (24>36:2).
Ме = 2047+1760·[((0,5·36)-10)/14]=3052,7141.
Задание 2
Связь между признаками – вложения в ценные бумаги и прибыль.
Решение.
Пусть y – прибыль банка.
i = 650-11/5=127,8.
Таким образом, получим следующие пять интервалов:
1) 11-138,8;
2) 138,8-266,6;
3) 266,6-394,4;
4) 394,4-522,2;
5) 522,2-650.
Построим корреляционную таблицу.
Таблица 2 – Корреляционная связь между прибылью и вложениями в ценные бумаги коммерческих банков
| Прибыль | Вложения в ценные бумаги | Итого | ||||
| 287-2047 | 2047-3807 | 3807-5567 | 5567-7327 | 7327-9087 | ||
| 11-138,8 | 8 | 3 | 3 | 14 | ||
| 138,8-266,6 | 6 | 2 | 2 | 10 | ||
| 266,6-394,4 | 1 | 3 | 4 | |||
| 394,4-522,2 | 1 | 2 | 2 | 5 | ||
| 522,2-650 | 2 | 1 | 3 | |||
| Итого | 10 | 14 | 7 | 3 | 2 | 36 |
Составим расчетную таблицу.
Таблица 3. Корреляционно-регрессионный анализ показателей коммерческих банков
| № п/п | Вложения в ценные бумаги | f | Прибыль | yi¯-yобщ¯ | (yi¯-yобщ¯)² | (yi¯-yобщ¯)²·f | |
| Всего | На 1 банк | ||||||
| 1 | 287-2047 | 10 | 1379 | 137.9 | -86.7389 | 7523.6348 | 75236.3485 |
| 2 | 2047-3807 | 14 | 3150 | 225 | 0.3611 | 0.1304 | 1.8256 |
| 3 | 3807-5567 | 7 | 1616 | 230.8571 | 6.2183 | 38.6667 | 270.6668 |
| 4 | 5567-7327 | 3 | 1062 | 354 | 129.3611 | 16734.2971 | 50202.8912 |
| 5 | 7327-9087 | 2 | 880 | 440 | 215.3611 | 46380.4082 | 92760.8164 |
| Итого | 36 | 8087 | 224.6389 | 218472.5484 |
Рассчитаем межгрупповую и общую дисперсию[2].
σ²м/г = (yi¯-yобщ¯)²·f / ∑f = 218472,5484/36=6068,68.
σ²общ = y²¯- (y¯)² = 2823993/36 – (224.6389)² = 78444.25 - 50462.635 = 27981.615.
Рассчитаем коэффициент детерминации:
η² = σ²м/г / σ²общ = 6068,68 / 27981,615 = 0,217- характеризует долю результативного признака, которая формируется под влиянием фактора, в данном случае она мала, связь между факторами непрямая. Доля вариации признака, которая формируется под влиянием неучтенных в задаче признаков составляет 0,783 (1-0,217).
Найдем эмпирическое корреляционное отношение:
η = 0,466, т.е. теснота связи между результативным признаком (y) и фактором признаком (x) – умеренная.
Задание 3
По результатам выполнения задания 1 с вероятностью 0,954 определите:
1. Ошибку выборки средней величины вложения средств банками в ценные бумаги и границы, в которых будет находится средняя величина вложений в генеральной совокупности.
2. Ошибку выборки доли банков с вложениями средств в ценные бумаги 3811 млн. руб. и более и границы, в которых будет находится генеральная доля.
Решение.
1. Имеем следующие данные:
n = 36, т.к. выборка механическая 3%-ная, то N = 36:0,03 = 1200, x˜=3233.6944 (для несгруппированных данных при 3%-ной выборке), простая дисперсия для несгруппированных данных равна σ² = 4829787,323.Для вероятности 0,954 находим t=2.
Δx˜= 2· ![]() ≈721,49.
≈721,49.
Таким образом, генеральная средняя будет находится в интервалах 3233,6944 – 721,49 ≤ x¯≤ 3233,6944 + 721,49,
2512,20 ≤ x¯≤ 3955,18.
Можно утверждать с вероятностью 0,954, что средняя величина вложений средств банками в ценные бумаги колеблется от 2512,20 до 3955,18 млн. руб.
2. По условию задачи n / N = 0.03 или 3%, выборочная доля (доля банков с вложениями средств в ценные бумаги 3811 млн. руб. и более равна w = 12/36 = 0,3333. Для вероятности 0,954 находим t=2. Предельную ошибку выборки определяем по формуле бесповторного отбора:
Δw = 2· ≈0.15.
≈0.15.
Предельная ошибка выборки, %:
Δ% = ![]() ·100 =
45%.
·100 =
45%.
Генеральная доля имеет находится в пределах:
w - Δw ≤ p ≤ w + Δw; тогда для нашей задачи находим 0.18 ≤ p ≤ 0.48.
Таким образом, с вероятностью 0,954 можно утверждать, что доля коммерческих банков с вложениями средств в ценные бумаги 3811 млн. руб. и более колеблется от 18 до 48%.
Задание 4
Имеются следующие данные по коммерческому банку о просроченной задолженности по кредитным ссудам:
| Год | Задолженность по кредиту, млн. руб. (y) | По сравнению с предыдущим годом |
абсол. знач. 1% прироста, млн. руб. (А%) |
||
| Абсолютный прирост, млн. руб. (Δy) |
Темп роста, % (Тр) |
Темп прироста, % (Тпр) |
|||
| 2000 | 1600 | - | - | - | - |
| 2001 | 1700 | +100 |
106,25 |
6.25 |
16 |
| 2002 | 1800 |
+100 |
105,88 | 5,88 | 17 |
| 2003 | 2340 | +540 | 130.0 |
30,0 |
18 |
| 2004 | 2538,9 | +198,9 |
108,5 |
8.5 | 23,4 |
Определите:
1. Задолженность по кредиту за каждый год.
2. Недостающие показатели анализа ряда динамики и внесите их в таблицу.
3. Основную тенденцию развития методом аналитического выравнивания.
Осуществите прогноз задолженности на следующие два года на основе найденного тренда.
Постройте графики. Сделайте выводы.
Решение.
1) Тпр (2001) = 106,25-100 = 6,25% по формуле Тпр = Тр-100;
2) Δy (2001) = 6.25·16 = +100 млн. руб. по формуле А% = Δy / Тпр;
3) y (2000) = 16·100 = 1600 млн. руб. по формуле А% = Δy / Тпр = 0,01yi-1;
4) y (2001) = 1600 + 100 = 1700 млн. руб.;
5) y (2002) = 1700+100 = 1800 млн. руб.;
6) Тр(2002) = (1800 / 1700) ·100 = 105,88%;
7) Тпр (2002) = 105,88-100 = 5,88%;
8) А% (2002) = 100 / 5,88 = 17 млн. руб.;
9) y (2003) = (130/100)·1800 = 2340 млн. руб.;
10) Δy (2003) = 2340-1800 = 540 млн. руб.;
11) А% (2003) = 540 / 30 = 18 млн. руб.;
12) у (2004) = (108,5 / 100)·2340 = 2538,9 млн. руб.;
13) Δу (2004) = 2538,9-2340 = 198,9 млн. руб.;
14) Тпр (2004) = 108,5-100 = 8,5%;
15) А% (2004) = 198,9 /8,5 = 23,4 млн. руб. [2, с. 287-298].
3. С помощью метода наименьших квадратов построим математическую модель, выражающую общую тенденцию изучаемого объекта. Для этого понадобятся данные следующей таблицы.
Таблица 4 – Построение линейной модели
| t | xt | t·xt | t² | xt^ | ε |
| 1 | 1600 | 1600 | 1 | 1492.22 | -107.78 |
| 2 | 1700 | 3400 | 4 | 1744 | 44 |
| 3 | 1800 | 5400 | 9 | 1995.78 | 195.78 |
| 4 | 2340 | 9360 | 16 | 2247.56 | -92.44 |
| 5 | 2538.9 | 12694.5 | 25 | 2499.34 | -39.56 |
| ∑ | 9978.9 | 32454.5 | 55 | 0 | |
| сред.зн. | 1995.78 | 6490.9 | 11 |
Линейная модель имеет вид: у = а1+ао·t. Найдем значения а1 и ао по формулам:
а1 = (t¯·xt - x¯· t¯) / (t²¯- (t¯)²) = (6490.9 – 1995.78·3) / (11-3²) = 503.56 / 2 = 251.78;
ао = x¯- a1· t¯ = 1995.78 – 251.78·3 = 1240.44.
Получили линейную модель y = 1240.44+251.78t.
Подставив в найденное уравнение t = 6, t = 7 получим точечные прогнозы на следующие два года. Прогнозная задолженность по кредиту на 2005 и 2006 соответственно равна 2751,12 и 3002,9 млн. руб.[2, с.298-317].
Фактические и расчетные данные по кредитной задолженности представлены в виде графика.
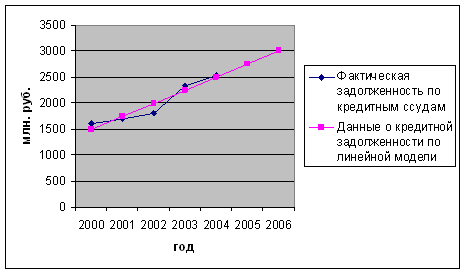
Рис. 1 – Просроченная задолженность по кредитным ссудам по коммерческому банку
3. Анализ некоторых аспектов деятельности Сберегательного банка РФ за 2006-2007 гг.
По данным расчётов, представленных в приложении 2, на основании консолидированного бухгалтерского баланса[3], следует отметить, что в целом в 2007 году наблюдается положительная динамика по всем показателям по сравнению с 2006 годом. Увеличение активной части баланса произошло в основном за счёт увеличения кредитов клиентам на 54,55%, а также за счёт увеличения торговых ценных бумаг на 16,89% и денежных средств на 15,57%.
К значительным изменениям в пассивной части баланса следует отнести увеличение средств других банков на 79,14%, средств клиентов на 52,74%, выпущенных долговых ценных бумаг на 32,41% и вкладов физических лиц на 31,08%. Заметно увеличилась величина эмиссионного дохода на 2321,22 млн. руб. Нераспределенная прибыль увеличилась на 48,35%.
Важнейшим показателем при анализе деятельности любого банка является величина и структура вкладов физических лиц и средств клиентов. Представим данную информацию графически.
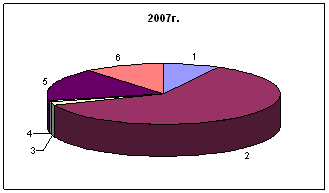
Рис. 2 – Структура вкладов и средств клиентов
1 – текущие счета физических лиц;
2 – срочные вклады физических лиц;
3 – расчётные счёта государственных и общественных организаций;
4 – срочные депозиты государственных и общественных организаций;
5 – расчётные счета прочих юридических лиц;
6 – срочные депозиты прочих юридических лиц.
Как видно из диаграммы, срочные вклады физических лиц занимают большую долю в структуре средств клиентов банка, по состоянию на 31 декабря 2007 они составили 2379647 млн. руб. при общей сумме вкладов и средств клиентов 3877620 млн. руб. Следует отметить, что Сбербанк остаётся на протяжении многих лет лидером среди других коммерческих банков по привлечению средств физических лиц во вклады, т.к. заслужил репутацию надёжного банка.
Наряду со вкладами в настоящее время одной из самых распространенных услуг банка является кредитование как физических, так и юридических лиц. По видам кредиты клиентам и средства в других банках можно разделить на следующие группы:
1 – коммерческое кредитование юридических лиц;
2 – специализированное кредитование юридических лиц;
3 – потребительские ссуды физическим лицам;
4 – жилищное кредитование физическим лицам;
5 – средства в других банках.
Заметим, что кредитование юридических лиц занимают большую долю в общей сумме выданных банком кредитов, это объясняется, прежде всего, размером кредита, ведь на развитие даже одного предприятия необходимы большие объёмы вложений, нежели на потребительские цели частных клиентов банка. Представим структуру кредитов, выданных банком, в динамике двух последних отчётных лет.
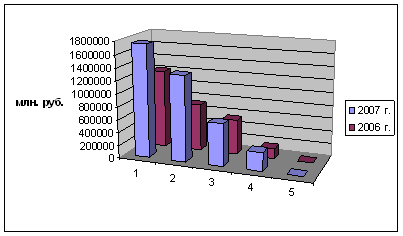
Рис. 3 – Динамика и структура кредитов и средств в других банках за 2006-2007гг.
Итак, структура практические не изменилась, а вот увеличение в абсолютном выражении на лицо.
Таким образом, при анализе отчётности Сбербанка РФ в целом наблюдается положительная динамика, что свидетельствует об устойчивом развитии, а репутация крупного надёжного банка позволяет ему оставаться лидером по привлечению средств физических и юридических лиц. Конечно, лишь этим деятельность банка не ограничивается, множество аспектов не были затронуты, но судить об общем направлении развития можно.
Заключение
Статистика – общественная наука, которая изучает количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной. Без статистических методов исследования невозможно представить анализ деятельности предприятия или изучение социально-экономического явления, поэтому роль статистики среди экономических наук значительна. Область применения статистики разнообразна, включая и банковскую деятельность.
Следует отметить, что статистика развивается и на основе её методов разрабатываются прикладные пакеты программ для ЭВМ, чтобы обеспечить удобство и простоту расчётов, а также сократить время анализа.
При выполнении данной работы применялся пакет прикладных программ обработки электронных таблиц MS Excel.
Список использованной литературы
1. Гусаров В.М. Статистика: Учеб. пособие для вузов. – М.: ЮНИТИ-ДАНА, 2001.
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. – М.: Инфра-М, 2003.
3. Башкирский вестник Сбербанка, 2007 №57.
4. www.sbrf.ru/ruswin/analitika/analitika.php.
Приложение 1
Расчётные данные к задаче
| x | y | x² | y² | x·y | σ² |
| 4069 | 110 | 16556761 | 12100 | 447590 | 697735.3711 |
| 4279 | 538 | 18309841 | 289444 | 2302102 | 1092663.704 |
| 3959 | 85 | 15673681 | 7225 | 336515 | 526068.1489 |
| 1032 | 60 | 1065024 | 3600 | 61920 | 4847458.427 |
| 4152 | 39 | 17239104 | 1521 | 161928 | 843285.0934 |
| 5347 | 153 | 28590409 | 23409 | 818091 | 4466060.371 |
| 2286 | 215 | 5225796 | 46225 | 491490 | 898124.76 |
| 2948 | 224 | 8690704 | 50176 | 660352 | 81621.31559 |
| 2914 | 203 | 8491396 | 41209 | 591542 | 102204.5378 |
| 1600 | 64 | 2560000 | 4096 | 102400 | 2668957.538 |
| 2145 | 11 | 4601025 | 121 | 23595 | 1185255.593 |
| 3811 | 153 | 14523721 | 23409 | 583083 | 333281.7045 |
| 889 | 121 | 790321 | 14641 | 107569 | 5497592.038 |
| 584 | 94 | 341056 | 8836 | 54896 | 7020880.649 |
| 990 | 105 | 980100 | 11025 | 103950 | 5034164.76 |
| 1618 | 93 | 2617924 | 8649 | 150474 | 2610468.538 |
| 1306 | 329 | 1705636 | 108241 | 429674 | 3716005.871 |
| 1981 | 451 | 3924361 | 203401 | 893431 | 1569243.371 |
| 9087 | 439 | 82573569 | 192721 | 3989193 | 34261185.93 |
| 8016 | 441 | 64256256 | 194481 | 3535056 | 22870446.43 |
| 7324 | 237 | 53640976 | 56169 | 1735788 | 16730599.54 |
| 3445 | 282 | 11868025 | 79524 | 971490 | 44650.03781 |
| 2079 | 191 | 4322241 | 36481 | 397089 | 1333319.26 |
| 2058 | 201 | 4235364 | 40401 | 413658 | 1382257.427 |
| 648 | 12 | 419904 | 144 | 7776 | 6685815.76 |
| 2673 | 77 | 7144929 | 5929 | 205821 | 314378.26 |
| 3145 | 282 | 9891025 | 79524 | 886890 | 7866.704475 |
| 2048 | 451 | 4194304 | 203401 | 923648 | 1405871.316 |
| 287 | 50 | 82369 | 2500 | 14350 | 8683008.149 |
| 2571 | 306 | 6610041 | 93636 | 786726 | 439163.9267 |
| 2081 | 440 | 4330561 | 193600 | 915640 | 1328704.482 |
| 3787 | 204 | 14341369 | 41616 | 772548 | 306147.0378 |
| 2131 | 63 | 4541161 | 3969 | 134253 | 1215935.038 |
| 7298 | 650 | 53260804 | 422500 | 4743700 | 16518579.65 |
| 4729 | 538 | 22363441 | 289444 | 2544202 | 2235938.704 |
| 7096 | 175 | 50353216 | 30625 | 1241800 | 14917404.2 |
| 116413 | 8087 | 550316415 | 2823993 | 32540230 | 173872343.6 |
| 3233.694 | 78444.25 | 4829787.323 |
Приложение 2
Анализ показателей консолидированного бухгалтерского баланса Сбербанка РФ за 2007 год
| 31 декабря 2006 | 31 декабря 2007 | Абсол. прирост | Темп роста | Темп прироста | Абсол. Зн. 1% прироста | |
| АКТИВЫ | ||||||
| Денежные средства и их эквиваленты | 209603 | 242231 | 32628 | 115.57 | 15.57 | 2096.03 |
| Обязательные резервы в ЦБ РФ | 77915 | 56790 | -21125 | 72.89 | -27.11 | 779.15 |
| Торговые ценные бумаги | 210641 | 246221 | 35580 | 116.89 | 16.89 | 2106.41 |
| Прочие ценные бумаги | 237847 | 247024 | 9177 | 103.86 | 3.86 | 2378.47 |
| Средства в других банках | 5631 | 5071 | -560 | 90.06 | -9.94 | 56.31 |
| Кредиты клиентам | 2537464 | 3921546 | 1384082 | 154.55 | 54.55 | 25374.64 |
| Инвестиционные ценные бумаги для продажи | х | 10094 | х | х | х | х |
| Инвест. ценные бумаги, удерживаемые до погашения | 26198 | х | х | х | х | х |
| Отложенный налоговый актив | х | 68 | х | х | х | х |
| Основные средства | 125216 | 146850 | 21634 | 117.28 | 17.28 | 1252.16 |
| Прочие активы | 36158 | 52913 | 16755 | 146.34 | 46.34 | 361.58 |
| ИТОГО АКТИВОВ | 3466673 | 4928808 | 1462135 | 142.18 | 42.18 | 34666.73 |
| ОБЯЗАТЕЛЬСТВА | ||||||
| Средства других банков | 44836 | 80321 | 35485 | 179.14 | 79.14 | 448.36 |
| Вклады физических лиц | 2046035 | 2681986 | 635951 | 131.08 | 31.08 | 20460.35 |
| Средства клиентов | 782789 | 1195634 | 412845 | 152.74 | 52.74 | 7827.89 |
| Выпущенные долговые ценные бумаги | 123729 | 163827 | 40098 | 132.41 | 32.41 | 1237.29 |
| Прочие заёмные средства | 107332 | 112025 | 4693 | 104.37 | 4.37 | 1073.32 |
| Отложенное налоговое обязательство | 3604 | х | х | х | х | х |
| Прочие обязательства | 22944 | 32754 | 9810 | 142.76 | 42.76 | 229.44 |
| Субординированный займ | 26880 | 25064 | -1816 | 93.24 | -6.76 | 268.8 |
| ИТОГО ОБЯЗАТЕЛЬСТВ | 3158149 | 4291611 | 1133462 | 135.89 | 35.89 | 31581.49 |
| СОБСТВЕННЫЕ СРЕДСТВА | ||||||
| Уставный капитал | 79981 | 87742 | 7761 | 109.70 | 9.70 | 799.81 |
| Эмиссионный доход | 10016 | 232493 | 222477 | 2321.22 | 2221.22 | 100.16 |
| Фонд переоценки зданий | 15344 | 14815 | -529 | 96.55 | -3.45 | 153.44 |
| Фонд переоценки инвест. ценных бумаг для продажи | х | 733 | х | х | х | х |
| Нераспределенная прибыль | 203183 | 301414 | 98231 | 148.35 | 48.35 | 2031.83 |
| ИТОГО СОБСТВЕННЫХ СРЕДСТВ | 308524 | 637197 | 328673 | 206.53 | 106.53 | 3085.24 |
| ИТОГО ОБЯЗАТЕЛЬСТВ И СОБСТВЕННЫХ СР-В | 3466673 | 4928808 | 1462135 | 142.18 | 42.18 | 34666.73 |
[1] Башкирский вестник Сбербанка, 2007 №57.
[2] Для расчёта в данном случае и ниже используются данные приложения 1.
[3] По данным сайта www.sbrf.ru