Учебное пособие: Множественная регрессия и корреляция
Множественная регрессия и корреляция
Пусть требуется построить линейную модель зависимости
некоторого выходного экономического показателя ![]() ,
называемого объясняемой переменной от набора входных показателей
,
называемого объясняемой переменной от набора входных показателей ![]() , называемых объясняющими
переменными. Основным методом построения таких моделей является метод
наименьших квадратов, смысл которого состоит в том, чтобы подобрать параметры
модели, минимизирующие суммы квадратов отклонений модельных значений
объясняемой переменной от истинных значений. Метод наименьших квадратов
реализован во всех статистических пакетах программ, а также в средствах
статистического пакета Анализа данных Microsoft Excel.
, называемых объясняющими
переменными. Основным методом построения таких моделей является метод
наименьших квадратов, смысл которого состоит в том, чтобы подобрать параметры
модели, минимизирующие суммы квадратов отклонений модельных значений
объясняемой переменной от истинных значений. Метод наименьших квадратов
реализован во всех статистических пакетах программ, а также в средствах
статистического пакета Анализа данных Microsoft Excel.
Пусть ![]() -
- ![]() наблюдений объясняемой
переменной, а
наблюдений объясняемой
переменной, а ![]() -
- ![]() наблюдений
наблюдений ![]() объясняющих переменных.
Задача состоит в построении по данной выборке линейной модели зависимости
объясняемой переменной от вектора объясняющих переменных.
объясняющих переменных.
Задача состоит в построении по данной выборке линейной модели зависимости
объясняемой переменной от вектора объясняющих переменных.
![]() .
.
Здесь ![]() –
коэффициенты модели, которые надо определить, а
–
коэффициенты модели, которые надо определить, а ![]() -
ошибка измерения модели.
-
ошибка измерения модели.
Для адекватной работы метода наименьших квадратов требуется выполнение следующих гипотез:
1.
![]() . (спецификация модели).
. (спецификация модели).
2.
![]() -детерминированные величины, причем
в матрице
-детерминированные величины, причем
в матрице

столбцы линейно независимые, т.е. ранг этой матрицы равен ![]() .
.
3.
![]() - случайная величина,
удовлетворяющая условиям
- случайная величина,
удовлетворяющая условиям
3а. ![]() , математическое
ожидание ошибки равно нулю;
, математическое
ожидание ошибки равно нулю;
3b. ![]() , дисперсия
ошибки не зависит от номера наблюдения;
, дисперсия
ошибки не зависит от номера наблюдения;
3с. ![]() , т.е. ошибки
разных наблюдений не зависят друг от друга.
, т.е. ошибки
разных наблюдений не зависят друг от друга.
Справедлива теорема Гаусса-Маркова, что при этих условиях метод наименьших квадратов дает наилучшую в некотором смысле модель. Если некоторые из условий не выполняются, то приходится использовать более сложные методы.
В результате применения метода наименьших квадратов находятся
оценки коэффициентов модели ![]() . По
этим оценкам и по значениям объясняющих переменных
. По
этим оценкам и по значениям объясняющих переменных ![]() строятся
модельные значения объясняемой переменной
строятся
модельные значения объясняемой переменной ![]() .
Обозначим через
.
Обозначим через ![]() отклонение
истинного значения объясняемой переменной от модельного для
отклонение
истинного значения объясняемой переменной от модельного для ![]() -го наблюдения (
-го наблюдения (![]() ). Качество модели
оценивается через сумму квадратов отклонений модели
). Качество модели
оценивается через сумму квадратов отклонений модели
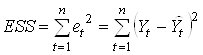 .
.
![]() ( error sum of squares) называется суммой квадратов
ошибок.
( error sum of squares) называется суммой квадратов
ошибок.
Метод наименьших квадратов состоит в том, что среди всех
возможных наборов коэффициентов модели находится набор, минимизирующий ![]() .
.
Если все коэффициенты модели, кроме константы ![]() , равны нулю, то
, равны нулю, то ![]() - среднему значению
объясняемой переменной. Тогда сумма квадратов отклонений равна
- среднему значению
объясняемой переменной. Тогда сумма квадратов отклонений равна
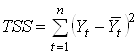 .
.
![]() ( total sum of squares) называется общей суммой
квадратов.
( total sum of squares) называется общей суммой
квадратов.
За счет того, что не все коэффициенты модели равны нулю, сумма квадратов отклонений уменьшается. В соответствии с этим величина
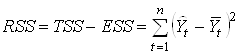
означает объясненную сумму квадратов (regression sum of squares).
После получения оценок ![]() необходимо
определить, все ли из них значимо отличаются от нуля, так как, если коэффициент
равен нулю, это означает, что соответствующая объясняющая переменная не
участвует в модели. Коэффициент значим, если гипотезу его равенства нулю надо
отвергнуть. Соответственно значимостью коэффициента называется вероятность того,
что его знак совпадает со знаком его оценки.
необходимо
определить, все ли из них значимо отличаются от нуля, так как, если коэффициент
равен нулю, это означает, что соответствующая объясняющая переменная не
участвует в модели. Коэффициент значим, если гипотезу его равенства нулю надо
отвергнуть. Соответственно значимостью коэффициента называется вероятность того,
что его знак совпадает со знаком его оценки.
Для полученной модели необходимо уметь определять, можно ли отбросить несколько входящих в нее объясняющих переменных или добавить переменные, не входящие в модель. С этой целью, проводят тест для определения какая модель лучше – «длинная» или «короткая». Также необходимо проверять однородность модели для разных наборов переменных. Для этого предназначен тест Чоу. Для оценки адекватности модели надо проверять тесты на выполнение условий теоремы Гаусса-Маркова.
Тест на выбор «длинной» или «короткой» регрессии
Данный тест используется для отбора наиболее существенных
объясняющих переменных. Например, переход от большого числа исходных
показателей состояния анализируемой системы к меньшему числу наиболее
информативных переменных может быть обусловлен дублированием информации,
доставляемой сильно взаимосвязанными признаками или неинформативностью
признаков, мало меняющихся при переходе от одного объекта к другому. Так, если
две какие-либо объясняющие переменные сильно коррелированы с результирующим
показателем ![]() и друг с
другом, то часто бывает достаточно включения в модель одной из них, а
дополнительным вкладом от включения другой можно пренебречь.
и друг с
другом, то часто бывает достаточно включения в модель одной из них, а
дополнительным вкладом от включения другой можно пренебречь.
Пусть ![]() .
Предположим, что модель не зависит от последних
.
Предположим, что модель не зависит от последних ![]() объясняющих
переменных и их можно исключить из модели. Это соответствует гипотезе
объясняющих
переменных и их можно исключить из модели. Это соответствует гипотезе
![]() ,
,
т.е. последние ![]() коэффициентов
коэффициентов
![]() равны
равны ![]() .
.
Тест по проверке данной гипотезы состоит в следующем:
1. Построить по МНК «длинную» (unrestricted) регрессию по
всем параметрам ![]() и найти для нее
и найти для нее ![]() .
.
2. Используя МНК, построить «короткую» (restricted) регрессию
по первым ![]() параметрам
параметрам ![]() и найти для нее
и найти для нее ![]() .
.
3. Вычислить F-статистику:
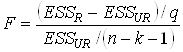
4. Найти критическую точку распределения Фишера при выбранном
уровне значимости ![]() :
: ![]() .
.
5. Если ![]() , то
гипотеза
, то
гипотеза ![]() отвергается, т.е. следует
использовать «длинную» модель.
отвергается, т.е. следует
использовать «длинную» модель.
Если ![]() , то гипотеза
, то гипотеза ![]() принимается, т.е. лучше
«короткая» модель.
принимается, т.е. лучше
«короткая» модель.
Тест Чоу на однородность зависимости объясняемой переменной от объясняющих
На практике нередки случаи, когда имеются две выборки пар
значений зависимой и объясняющей переменных ![]() .
Например, одна выборка пар значений переменных объемом
.
Например, одна выборка пар значений переменных объемом ![]() получена при одних
условиях, а другая, объемом
получена при одних
условиях, а другая, объемом ![]() , -
при несколько измененных условиях. Необходимо выяснить, действительно ли две
выборки однородны в регрессионном смысле? Другими словами, можно ли объединить
две выборки в одну и рассматривать единую модель регрессии
, -
при несколько измененных условиях. Необходимо выяснить, действительно ли две
выборки однородны в регрессионном смысле? Другими словами, можно ли объединить
две выборки в одну и рассматривать единую модель регрессии ![]() по
по ![]() (гипотеза
(гипотеза ![]() )?
)?
Для проверки гипотезы ![]() применяется
тест Чоу (Chow), состоящий в следующем:
применяется
тест Чоу (Chow), состоящий в следующем:
1. Используя МНК, построить модель по выборке объемом ![]() и найти для нее
и найти для нее ![]() .
.
2. Пусть есть основание предполагать, что вся выборка состоит
из двух подвыборок объемами ![]() и
и ![]() соответственно. Для каждой
из них строится линейная регрессия.
соответственно. Для каждой
из них строится линейная регрессия.![]() - сумма
квадратов отклонений значений
- сумма
квадратов отклонений значений ![]() от
регрессионных значений
от
регрессионных значений ![]() , посчитанных по
первой подвыборке,
, посчитанных по
первой подвыборке, ![]() – сумма
квадратов отклонений значений
– сумма
квадратов отклонений значений ![]() от
регрессионных значений
от
регрессионных значений ![]() , посчитанных по
второй подвыборке.
, посчитанных по
второй подвыборке.
![]()
3. Вычислить F – статистику:
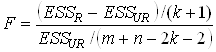 ,
,
где ![]() –
число объясняющих переменных модели.
–
число объясняющих переменных модели.
4. Найти критическую точку распределения Фишера при выбранном
уровне значимости ![]() .
.
5. Если ![]() , то мы
можем объединить две выборки в одну. Если
, то мы
можем объединить две выборки в одну. Если ![]() ,
то необходимо использовать две модели.
,
то необходимо использовать две модели.
Тесты на гетероскедастичность
Гомоскедастичность – дисперсия каждого отклонения ![]() одинакова
для всех значений
одинакова
для всех значений ![]() .
.
Гетероскедастичность – дисперсия объясняемой переменной (следовательно, и случайных ошибок) непостоянна.
В тестах на гетероскедастичность проверяется основная
гипотеза ![]() (т.е. модель
гомоскедастична) против альтернативной гипотезы
(т.е. модель
гомоскедастична) против альтернативной гипотезы ![]() :
не
:
не ![]() (т.е. модель гетероскедастична).
(т.е. модель гетероскедастична).
Тест Гольдфельда – Куандта (Goldfeld - Quandt)
Этот тест применяется, как правило, когда есть предположение о прямой зависимости дисперсии ошибок от величины некоторой объясняющей переменной, входящей в модель.
Предполагается, что ![]() имеет
нормальное распределение. Тест включает в себя следующие шаги:
имеет
нормальное распределение. Тест включает в себя следующие шаги:
1. Упорядочить данные по убыванию (или по возрастанию) той независимой переменной, относительно которой есть подозрение на гетероскедастичность.
2. Исключить ![]() средних
(в этом упорядочении) наблюдений (
средних
(в этом упорядочении) наблюдений (![]() , где
, где ![]() – общее количество
наблюдений).
– общее количество
наблюдений).
3. Провести две независимых регрессии первых 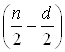 наблюдений и последних
наблюдений и последних 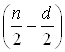 наблюдений и найти,
соответственно,
наблюдений и найти,
соответственно, ![]() и
и ![]() . Из
. Из ![]() и
и ![]() выбираем большую и меньшую
величины, соответственно,
выбираем большую и меньшую
величины, соответственно, ![]() и
и ![]() .
.
4. Составить статистику 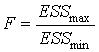 и
найти по распределению Фишера
и
найти по распределению Фишера 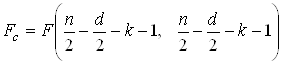 , где
, где ![]() – число объясняющих
переменных модели.
– число объясняющих
переменных модели.
5. Если ![]() , то
гипотеза
, то
гипотеза ![]() отвергается, т.е. модель
гетероскедастична, а если
отвергается, т.е. модель
гетероскедастична, а если ![]() , то
гипотеза
, то
гипотеза ![]() принимается, т.е. модель
гомоскедастична.
принимается, т.е. модель
гомоскедастична.
Тест Бреуша – Пагана (Breusch - Pagan)
Этот тест применяется в тех случаях, когда предполагается,
что дисперсии ![]() зависят от
некоторых дополнительных переменных. Пусть
зависят от
некоторых дополнительных переменных. Пусть ![]() ,
,
![]() . Тест состоит в следующем:
. Тест состоит в следующем:
1. Провести обычную регрессию и получить ![]() . (Для этого в диалоговом
окне Регрессия установить флажок на функцию Остатки)
. (Для этого в диалоговом
окне Регрессия установить флажок на функцию Остатки)
2. Построить оценку ![]() .
.
3. Провести регрессию 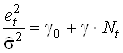 и найти для нее
объясненную часть вариации
и найти для нее
объясненную часть вариации ![]() .
.
4. Построить статистику ![]() .
.
5. Если ![]() (где p
– число переменных, от которых зависит
(где p
– число переменных, от которых зависит ![]() ),
то имеет место гетероскедастичность.
),
то имеет место гетероскедастичность.
Если ![]() , то -
гомоскедастичность.
, то -
гомоскедастичность.
![]() - критическая точка распределения
- критическая точка распределения ![]() (хи-квадрат) при выбранном
уровне значимости
(хи-квадрат) при выбранном
уровне значимости ![]() , для нахождения
которой выполнить следующую последовательность действий: fx
, для нахождения
которой выполнить следующую последовательность действий: fx![]() Статистические
Статистические![]() ХИ2ОБР
ХИ2ОБР
![]()
Тест Дарбина – Уотсона (Darbin-Watson) на наличие автокорреляции
Этот тест используется для обнаружения автокорреляции первого
порядка, т.е. проверяется некоррелированность не любых, а только соседних
величин ![]() . Соседними обычно
считаются соседние во времени (при рассмотрении временных рядов) или по
возрастанию объясняющей переменной
. Соседними обычно
считаются соседние во времени (при рассмотрении временных рядов) или по
возрастанию объясняющей переменной ![]() значения
значения
![]() .
.
![]()
Гипотеза ![]() (автокорреляция
отсутствует).
(автокорреляция
отсутствует).
Общая схема критерия Дарбина – Уотсона следующая:
1. По эмпирическим данным построить уравнение регрессии по
МНК и определить значения отклонений ![]() для
каждого наблюдения t (t = 1, 2, …, n).
для
каждого наблюдения t (t = 1, 2, …, n).
2. Рассчитать статистику DW:
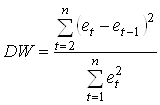
3. По таблице критических точек распределения Дарбина
–Уотсона для заданного уровня значимости ![]() ,
числа наблюдений
,
числа наблюдений ![]() и количества
объясняющих переменных
и количества
объясняющих переменных ![]() определить два
значения:
определить два
значения: ![]() - нижняя граница и
- нижняя граница и ![]() - верхняя граница (таблица
2).
- верхняя граница (таблица
2).
Полный вариант таблицы приведен в разделе Математико-статистические таблицы (Таблица 5. Значения dH и dB критерия Дарбина—Уотсона на уровне значимости = 0,05 (n — число наблюдений, р — число объясняющих переменных). множественный корреляция регрессия
Таблица 2.
| Статистика Дарбина – Уотсона, уровень значимости 0,05 | |||||||||||
|
|
1 | 2 | 3 | 4 | 5 | |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
20 | 1,20 | 1,41 | 1,1 | 1,54 | 1,00 | 1,67 | 0,90 | 1,83 | 0,79 | 1,99 |
|
21 | 1,22 | 1,42 | 1,13 | 1,54 | 1,03 | 1,66 | 0,93 | 1,81 | 0,83 | 1,96 |
|
22 | 1,24 | 1,43 | 1,15 | 1,54 | 1,05 | 1,66 | 0,96 | 1,80 | 0,86 | 1,94 |
|
23 | 1,26 | 1,44 | 1,17 | 1,54 | 1,08 | 1,66 | 0,99 | 1,79 | 0,90 | 1,92 |
|
24 | 1,27 | 1,45 | 1,19 | 1,55 | 1,10 | 1,66 | 1,01 | 1,78 | 0,93 | 1,90 |
|
25 | 1,29 | 1,45 | 1,21 | 1,55 | 1,12 | 1,66 | 1,04 | 1,77 | 0,95 | 1,89 |
4. Сделать выводы по правилу:
![]() - существует положительная автокорреляция (
- существует положительная автокорреляция (![]() ),
), ![]() отвергается;
отвергается;
![]() - вывод о наличии автокорреляции не определен;
- вывод о наличии автокорреляции не определен;
![]() - автокорреляция отсутствует,
- автокорреляция отсутствует, ![]() принимается;
принимается;
![]() - вывод о наличии автокорреляции не определен;
- вывод о наличии автокорреляции не определен;
![]() - существует отрицательная автокорреляция (
- существует отрицательная автокорреляция (![]() ),
), ![]() отвергается.
отвергается.