Реферат: Вибір оптимальних варіантів систем методами векторної оптимізації
ВИБІР ОПТИМАЛЬНИХ ВАРІАНТІВ СИСТЕМ МЕТОДАМИ ВЕКТОРНОЇ ОПТИМІЗАЦІЇ
Вступ
проектування оптимальна система векторна оптимізація
Початкові етапи проектування оптимальних систем базуються на основних положеннях теорії векторної (багатокритеріальної) оптимізації. Векторна оптимізація визначає правила вибору оптимальних проектних рішень - варіантів побудови системи з урахуванням сукупності показників якості системи. Методи векторної оптимізації набули бурхливого розвитку як у галузі загальносистемного аналізу, так і у галузі радіотехнічних систем, зокрема, систем електрозв’язку. Це було визвано об'єктивною необхідністю враховувати при проектуванні сукупність, як правило, протирічивих техніко-економічних вимог до системи. Основні положення векторної оптимізації використовуються в задачах синтезу і аналізу системи, коли створюється проект оптимальної системи з використанням математичних моделей повідомлень, сигналів, завад, критеріїв оптимальності, а також методів вибору оптимальних проектних рішень.
В даному розділі розглядається формалізована постановка та основні особливості розв'язання задач векторної оптимізації, що виникають на початкових етапах проектування системи при виборі оптимальних варіантів за сукупністю показників якості. Основні положення теорії векторної оптимізації викладені на основі систематизації та узагальнення вказаних вище робіт.
1 Постановка задачі проектування оптимальної системи
При проектуванні систем постановка задачі відіграє важливу роль. Недаром
кажуть, що правильна постановка задачі наполовину дає її успішне розв'язання. Розглянемо особливості та проблеми постановки задачі проектування
оптимальної системи з урахуванням сукупності показників якості. Альтернативне проектне рішення ![]() - це варіант побудови системи
- це варіант побудови системи ![]() . У
загальному вигляді систему можна подати як упорядковану множину елементів,
відносин між ними та їх властивостей. Їх однозначне задавання цілком визначає
побудову й ефективність системи. Вважатимемо, що варіант побудови системи
. У
загальному вигляді систему можна подати як упорядковану множину елементів,
відносин між ними та їх властивостей. Їх однозначне задавання цілком визначає
побудову й ефективність системи. Вважатимемо, що варіант побудови системи ![]() задається структурою
задається структурою ![]() і вектором параметрів
і вектором параметрів ![]() . Для інформаційних систем
також повинна бути задана множина вхідних впливів
. Для інформаційних систем
також повинна бути задана множина вхідних впливів ![]() і
результатів роботи системи
і
результатів роботи системи ![]() , що
фактично визначає систему
, що
фактично визначає систему ![]() як
відображення множини
як
відображення множини ![]() на множину Y -
на множину Y -
![]() .
.
Ці абстрактні означення системи повинні бути конкретизовані в процесі проектування. Зокрема, для інформаційної системи множина вхідних впливів - це множина сигналів і завад, що повинні бути описані певними математичними моделями. При проектуванні має бути визначена структура системи як сукупність відповідних елементів і зв'язків між ними, а також повинні бути отримані значення параметрів цієї системи.
Вихідні дані для
проектування системи включать: сукупність умов роботи системи ![]() та обмежень на умови
роботи, на структуру і параметри системи
та обмежень на умови
роботи, на структуру і параметри системи ![]() ;
сукупність показників якості
;
сукупність показників якості ![]() та
обмежень на значення цих показників якості
та
обмежень на значення цих показників якості ![]() ;
критерій оптимальності системи.
;
критерій оптимальності системи.
Розглянемо приклади вихідних даних при проектуванні систем зв'язку. До
умов роботи ![]() системи зв'язку може
відноситись: вид і характеристики повідомлень, сигналів, завад, каналів
зв'язку. Обмеження на структуру системи
системи зв'язку може
відноситись: вид і характеристики повідомлень, сигналів, завад, каналів
зв'язку. Обмеження на структуру системи ![]() залежно
від конкретної задачі можуть бути задані як слабкі, так і жорсткі. Зокрема, це
загальні вимоги до класу систем зв'язку, наприклад, вимоги, щоб система була
одноканальною, мала вільний доступ, не включала зворотного (службового) каналу,
ретрансляторів. За більш жорсткіших обмежень
задається принцип роботи системи, вид модуляції, декомпозиція системи і навіть
повністю структура, а в процесі оптимізації варіюється лише вектор внутрішніх
параметрів системи. При цьому обмеження на параметри системи (наприклад,
параметри модуляції, потужність сигналу або завади, число каналів) можуть бути
типу рівностей, нерівностей
або деякого функціонального
зв'язку.
залежно
від конкретної задачі можуть бути задані як слабкі, так і жорсткі. Зокрема, це
загальні вимоги до класу систем зв'язку, наприклад, вимоги, щоб система була
одноканальною, мала вільний доступ, не включала зворотного (службового) каналу,
ретрансляторів. За більш жорсткіших обмежень
задається принцип роботи системи, вид модуляції, декомпозиція системи і навіть
повністю структура, а в процесі оптимізації варіюється лише вектор внутрішніх
параметрів системи. При цьому обмеження на параметри системи (наприклад,
параметри модуляції, потужність сигналу або завади, число каналів) можуть бути
типу рівностей, нерівностей
або деякого функціонального
зв'язку.
Вектор показників якості ![]() включає сукупність зовнішніх параметрів
системи зв'язку, що характеризують основні тактико-технічні характеристики
системи (швидкість передавання повідомлень, імовірність похибок передавання,
пропускну здатність, надійність). При постановці задачі задаються не числові
значення, а лише склад показників якості, які повинні враховуватися при
оптимізації системи. На початкових етапах проектування, як правило, до уваги
беруть лише найбільш важливі показники. Обмеження
включає сукупність зовнішніх параметрів
системи зв'язку, що характеризують основні тактико-технічні характеристики
системи (швидкість передавання повідомлень, імовірність похибок передавання,
пропускну здатність, надійність). При постановці задачі задаються не числові
значення, а лише склад показників якості, які повинні враховуватися при
оптимізації системи. На початкових етапах проектування, як правило, до уваги
беруть лише найбільш важливі показники. Обмеження ![]() що
накладаються на числові значення показників якості, можуть бути також типу рівностей, нерівностей або функціонального зв'язку.
що
накладаються на числові значення показників якості, можуть бути також типу рівностей, нерівностей або функціонального зв'язку.
Системи, які задовольняють сукупність даних ![]() ,
називають допустимими, а такі системи, які задовольняють ще й обмеження на
значення показників якості
,
називають допустимими, а такі системи, які задовольняють ще й обмеження на
значення показників якості ![]() -
строго допустимими. Раніше при проектуванні систем обмежувалися вибором строго
допустимих систем. З ускладненням і збільшенням вартості систем, що
проектуються, актуальним стає пошук оптимальних за сукупністю показників якості
систем.
-
строго допустимими. Раніше при проектуванні систем обмежувалися вибором строго
допустимих систем. З ускладненням і збільшенням вартості систем, що
проектуються, актуальним стає пошук оптимальних за сукупністю показників якості
систем.
З усіх строго допустимих систем оптимальною (найкращою) є та система,
якій відповідає найкраще (у раніше встановленому розумінні) значення вектора ![]() . Для вибору оптимальної
системи слід обрати чи обґрунтувати критерій переваги однієї системи над другою
(критерій оптимальності), тобто правило, на основі якого одне значення вектора
. Для вибору оптимальної
системи слід обрати чи обґрунтувати критерій переваги однієї системи над другою
(критерій оптимальності), тобто правило, на основі якого одне значення вектора ![]() слід визнати кращим порівняно
з іншим його значенням.
слід визнати кращим порівняно
з іншим його значенням.
Таким чином, задача проектування оптимальної системи формулюється так:
знайти таку систему, яка задовольняє сукупності вихідних даних ![]() і при цьому має
значення вектора показників якості
і при цьому має
значення вектора показників якості ![]() , найкраще за обраним критерієм переваги.
, найкраще за обраним критерієм переваги.
Проектування, що проводиться з урахуванням сукупності показників якості ![]() , називають векторним синтезом (векторною
оптимізацією, оптимізацією за векторним критерієм, багатокритеріальною
оптимізацією). На відмінність від цього синтез системи з урахуванням одного
показника якості
, називають векторним синтезом (векторною
оптимізацією, оптимізацією за векторним критерієм, багатокритеріальною
оптимізацією). На відмінність від цього синтез системи з урахуванням одного
показника якості ![]() називається
скалярним.
називається
скалярним.
Залежно від сформульованих вихідних даних знаходження оптимальної системи може зводиться до розв'язання різних у математичному відношенні оптимізаційних задач:
1. Синтез оптимальної структури системи, що означає знаходження оптимального оператора системи.
Параметрична оптимізація, тобто вибір оптимальних значень параметрів системи при заданій її структурі.
3. Дискретний вибір оптимальних варіантів системи із скінченного числа допустимих варіантів.
Математичні методи оптимізації параметрів і дискретного вибору добре розвинуті й широко використовуються при проектуванні систем. Синтез структури системи є складнішою задачею і часто наштовхується на труднощі не лише математичного, а й принципового характеру, що зв'язані з інформаційною невизначеністю при формулюванні умов роботи системи, а також при виборі узагальненої цільової функції системи.
В останньому випадку виникає непроста задача «апроксимації» функції вибору оптимальної системи, яка є в уяві замовника системи, іншою функцією вибору, що формалізується у вигляді певного критерію оптимальності з використанням строгих математичних методів. Як правило, відразу не вдається вибрати глобальний критерій оптимальності у вигляді скалярної цільової функції, що включає сукупність показників якості, і оптимізація якої привела б до вибору єдиного варіанта системи. Тому доводиться вводити сукупність цільових функцій, зв'язанних з відповідними показниками якості, що приводить до необхідності розв'язання задач векторної оптимізаціі. При введенні векторної цільової функції
![]() (1)
(1)
множина
допустимих варіантів системи ![]() відображується
у критеріальний простір векторних оцінок
відображується
у критеріальний простір векторних оцінок ![]() .
Це дає можливість порівнювати варіанти системи між собою у критеріальному
просторі
.
Це дає можливість порівнювати варіанти системи між собою у критеріальному
просторі ![]() і вибирати оптимальні
варіанти системи. Вибір оптимальних варіантів системи пов'язаний з певним
критерієм оптимальності.
і вибирати оптимальні
варіанти системи. Вибір оптимальних варіантів системи пов'язаний з певним
критерієм оптимальності.
2 Формування множини припустимих варіантів системи на основі морфологічного підходу
При задаванні множини припустимих варіантів технічних систем широкого застосування набув морфологічний підхід, для якого характерні такі чинники:
-виявлення максимального
переліку основних функцій системи та декомпозиція системи на підсистеми за
функціональними ознаками ![]() ;
;
-визначення різних
альтернативних способів реалізації кожної підсистеми і задання припустимих
варіантів їх побудови ![]() ;
;
-формування різних варіантів
побудови системи в цілому на основі морфологічних класів – множини варіантів
побудови кожної підсистеми, для яких виконуються умови ![]() ,
, ![]() .
.
Формується
морфологічна таблиця (табл. 1). Кожен варіант побудови системи визначаеться різними можливими варіантами підсистем. При формуванні припустимої множини
варіантів системи повинні враховуватися обмеження на структуру, параметри і
технічну реалізацію окремих підсистеми та системи в цілому, а також припустимі
комбінації поєднання окремих варіантів підсистем між собою. Кількість можливих
варіантів системи визначається так:  .
.
Таблиця 1 - Морфологічна таблиця для задання множини припустимих варіантів системи
| Морфологічні класи |
Можливі способи реалізації підсистеми |
Кількість способів реалізації системи |
|
|
|
|
|
|
|
|
| .... | ... | ... |
|
|
|
|
| ... | ... | ... |
|
|
|
|
3 Вибір критерію оптимальності системи
Дуже важливим при розв'язанні задач оптимізації є питання вибору критерію оптимальності системи. Саме критерій оптимальності визначає істинну цінність проектованої системи. Ніякі зручності математичного чи іншого характеру не можуть компенсувати шкідливих наслідків застосування неадекватного критерію оптимальності системи.
Вибір критерію оптимальності, як уже зазначалося, зв'язаний з формалізацією уяви замовника системи про її оптимальність. Існує два підходи до опису переваги одного варіанта системи над іншим: ординалістичний і кардиналістичний.
Кардиналістичний підхід до опису переваги замовника приписує кожній системі ![]() якесь числове значення функції корисності
якесь числове значення функції корисності ![]() .
Функція корисності визначає відповідний порядок (або перевагу)
.
Функція корисності визначає відповідний порядок (або перевагу) ![]() на множині
на множині ![]() тоді і тільки тоді, коли для різних варіантів
тоді і тільки тоді, коли для різних варіантів ![]() виконуєтся нерівність
виконуєтся нерівність ![]() . У цьому випадку кажуть, що функція корисності
. У цьому випадку кажуть, що функція корисності ![]() є індикатором переваги
є індикатором переваги ![]() . Фактично цей
підхід зв'язаний із заданням такої скалярної цільової функції,
оптимізація якої у загальному випадку може привести до вибору єдиного найкращого варіанту системи.
. Фактично цей
підхід зв'язаний із заданням такої скалярної цільової функції,
оптимізація якої у загальному випадку може привести до вибору єдиного найкращого варіанту системи.
Однак на початкових етапах проектуваннях систем задати скалярну функцію корисності досить складно, тому спочатку вводять сукупність показників якості та зв’язаних з ними цільових функцій (1). Це пов'язано з такими причинами: багатогранність технічних вимог, які висуваються до проектуємої системи; необхідність забезпечення оптимальності системи за різних умов її роботи; система складається з декількох взаємозалежних між собою підсистем і оптимальність системи в цілому визначається ефективністю її складових частин.
У зв’язку з тим, що систему ![]() доводиться характеризувати сукупністю показників
якості (цільових функції), це ускладнює процес вибору оптимальних
варіантів систем. При цьому мають
місце три випадки: показники якості не пов'язані між собою; показники якості зв'язані між собою, але є узгодженими; показники якості зв'язані між
собою і є конкуруючими (антагоністичними).
доводиться характеризувати сукупністю показників
якості (цільових функції), це ускладнює процес вибору оптимальних
варіантів систем. При цьому мають
місце три випадки: показники якості не пов'язані між собою; показники якості зв'язані між собою, але є узгодженими; показники якості зв'язані між
собою і є конкуруючими (антагоністичними).
У першому випадку знаходження оптимальних варіантів системи виконується шляхом оптимізації по кожній із цільових функцій незалежно
![]() . (2)
. (2)
У другому випадку оптимальні варіанти можуть знаходитися також шляхом оптимізації окремих цільових функцій, тобто цей випадок близький до першого.
У третьому випадку оптимуми по різним цільових функціях не збігаються. Розв’язанням цієї задачі є узгоджений оптимум цільових функцій. Узгоджений оптимум полягає в тому, що досягається мінімальне (максимальне) значення кожнієї цільової функції за умови, що інші цільові функції приймають фіксовані, але довільні значення.
Ординалістичний підхід апелює до порядку (краще-гірше) і базується на введенні певних бінарних відношень на множині допустимих
систем. У цьому випадку поняття переваги замовника системи - це бінарне
відношення ![]() на множині допустимих
систем
на множині допустимих
систем ![]() , яке відображує уяву
замовника системи, що система
, яке відображує уяву
замовника системи, що система ![]() краща
за систему
краща
за систему ![]() :
: ![]() .
.
На практиці часто при виборі системи на множині ![]() можна керуватися
відношенням строгої переваги
можна керуватися
відношенням строгої переваги ![]() , що є асиметричним і транзитивним. При
цьому система
, що є асиметричним і транзитивним. При
цьому система ![]() називається оптимальною
за відношенням
називається оптимальною
за відношенням ![]() , якщо не існує іншої системи
, якщо не існує іншої системи ![]() , для якої справедливе
відношення
, для якої справедливе
відношення ![]() . Множина оптимальних систем за
відношенням
. Множина оптимальних систем за
відношенням ![]() означається як
означається як ![]() . Залежно від структури допустимої множини
. Залежно від структури допустимої множини ![]() і властивостей відношення
і властивостей відношення ![]() множина оптимальних систем може включати єдиний
елемент, скінченне або нескінченне число елементів. Якщо відношення нероздільності
збігається з відношенням рівності
множина оптимальних систем може включати єдиний
елемент, скінченне або нескінченне число елементів. Якщо відношення нероздільності
збігається з відношенням рівності ![]() , то
множина
, то
множина ![]() (якщо вона не порожня) складається з єдиного
елемента.
(якщо вона не порожня) складається з єдиного
елемента.
Із введенням сукупності цільових функцій кожна система відображується на
простір векторних оцінок (критеріальний простір). При цьому
вказане відношення строгої переваги існує і для оцінок. Узгодженість відношення переваги на множині
проектних рішень ![]() і просторі векторних оцінок
і просторі векторних оцінок ![]() встановлює аксіома Парето. Згідно з нею для будь-яких двох векторних оцінок
встановлює аксіома Парето. Згідно з нею для будь-яких двох векторних оцінок ![]() , що
задовольняють векторну нерівність
, що
задовольняють векторну нерівність ![]() ,
завжди виконується відношення
,
завжди виконується відношення ![]() .
.
Множину оптимальних оцінок відносно ![]() на просторі
на просторі ![]() називають
множиною Парето-оптимальних (оптимальних за Парето) або ефективних оцінок і
позначають
називають
множиною Парето-оптимальних (оптимальних за Парето) або ефективних оцінок і
позначають ![]() . Включення
. Включення ![]() має місце тоді і
тільки тоді, коли немає оцінок, для яких виконується нерівність
має місце тоді і
тільки тоді, коли немає оцінок, для яких виконується нерівність ![]() . Такий критерій вибору оптимальних рішень
називають безумовним критерієм переваги (БКП) або критерієм Парето.
. Такий критерій вибору оптимальних рішень
називають безумовним критерієм переваги (БКП) або критерієм Парето.
Проектні рішення, тобто варіанти побудови системи ![]() , для
яких справджується включення
, для
яких справджується включення ![]() називають
Парето-оптимальними відносно векторної цільової функції
називають
Парето-оптимальними відносно векторної цільової функції ![]() на множині
на множині ![]() і позначають як
і позначають як ![]() . Іншими словами,
. Іншими словами, ![]() тоді і тільки тоді, коли не існує такої системи
тоді і тільки тоді, коли не існує такої системи ![]() , для якої виконується векторна
нерівність.
, для якої виконується векторна
нерівність.
![]() . (3)
. (3)
Співвідношення (3) означає, що виконуються нерівності ![]() для всіх
для всіх ![]() і принаймні для одного з показників якості
виконується строга нерівність.
і принаймні для одного з показників якості
виконується строга нерівність.
Слід зазначити, що відношення строгої переваги ![]() , яке має місце для векторних оцінок, перетворюється при
, яке має місце для векторних оцінок, перетворюється при ![]() на відношення
на відношення ![]() для скалярних оцінок. При
цьому Парето-оптимальна оцінка збігається з максимальним елементом множини
для скалярних оцінок. При
цьому Парето-оптимальна оцінка збігається з максимальним елементом множини ![]() , якому відповідає оптимум скалярної
цільової функції
, якому відповідає оптимум скалярної
цільової функції ![]() . Таким чином, поняття Парето-оптимальності слід
розглядати як узагальнення поняття оптимуму на випадок кількох цільових
функцій. При цьому оптимум за Парето - це узгоджений
оптимум зв'язаних між собою і конкуруючих показників якості системи.
. Таким чином, поняття Парето-оптимальності слід
розглядати як узагальнення поняття оптимуму на випадок кількох цільових
функцій. При цьому оптимум за Парето - це узгоджений
оптимум зв'язаних між собою і конкуруючих показників якості системи.
Для Парето-оптимальних проектних рішень характерні такі властивості:
1. Усі елементи множини
допустимих варіантів системи ![]() , що не належать до множини Парето-оптимальних
, що не належать до множини Парето-оптимальних ![]() ,
є безумовно гіршими.
,
є безумовно гіршими.
Жодна Парето-оптимальна система з множини ![]() не може бути визнана
безумовно гіршою або кращою порівняно з іншою системою цієї множини. Це
означає, що всі вони є незрівнянними за критерієм Парето - безумовним критерієм
переваги.
не може бути визнана
безумовно гіршою або кращою порівняно з іншою системою цієї множини. Це
означає, що всі вони є незрівнянними за критерієм Парето - безумовним критерієм
переваги.
3. Якщо множина ![]() узгоджена, тобто містить лише один елемент (систему), то відповідний варіант системи є найкращим.
узгоджена, тобто містить лише один елемент (систему), то відповідний варіант системи є найкращим.
4. Кожній
Парето-оптимальній системі відповідає потенціально можливе значення кожного із
показників якості ![]() , що може бути
досягнуто за фіксованих, але довільних значень інших
, що може бути
досягнуто за фіксованих, але довільних значень інших ![]() показників якості. Це
властивість
показників якості. Це
властивість ![]() -кратного оптимуму.
Сукупність таких оптимальних значень показників якості є багатовимірними
потенціальними характеристиками системи (БПХ).
-кратного оптимуму.
Сукупність таких оптимальних значень показників якості є багатовимірними
потенціальними характеристиками системи (БПХ).
5. Оптимальна поверхня, що є геометричним місцем Парето-оптимальних оцінок, має строго монотонний характер, тобто кожна із функцій
![]() ,
,
![]() , (4)
, (4)
..........................
![]()
для Парето-оптимальних оцінок монотонно спадає щодо кожного з аргументів. Ці залежності називаються багатовимірними діаграмами обміну (БДО) для Парето-оптимальних систем.
Порівняно з одновимірними потенціальними характеристиками системи БПХ та зв'язані з ними БДО характеризуються двома важливими властивостями. По-перше, вони дають найкраще (потенціальне можливе) значення не одного, а кожного з обраних показників якості. По-друге, вони вказують, яким чином слід змінити значення одних показників якості для поліпшення інших показників якості і за рахунок якої зміни структури чи параметрів системи це можна зробити.
4 Деякі методи знаходження Парето-оптимальних рішень
Більшість методів знаходження Парето-оптимальних рішень базується на тих
чи інших умовах Парето-оптимальності. У загальному випадку використовуються
достатні й необхідні умови Парето-оптимальності. Зокрема, рішення є
Парето-оптимальним, якщо воно є рішеннями задачі максимізації певної функції,
зростаючої за відношенням ![]() .
Фактично розв'язання задачі Парето-оптимізації зводиться до множини відповідних
задач скалярної оптимізації за деяких обмежень. Якщо використані умови
оптимальності є також і достатніми, то знайдена у такій спосіб множина рішень є
множиною Парето-оптимальних рішень. У противному випадку, знайдена множина може
включати і зайві рішення, що мають бути відкинуті.
.
Фактично розв'язання задачі Парето-оптимізації зводиться до множини відповідних
задач скалярної оптимізації за деяких обмежень. Якщо використані умови
оптимальності є також і достатніми, то знайдена у такій спосіб множина рішень є
множиною Парето-оптимальних рішень. У противному випадку, знайдена множина може
включати і зайві рішення, що мають бути відкинуті.
Знаходження множини Парето-оптимальних систем може здійснюватися або безпосередньо перебиранням усіх строго допустимих варіантів системи та перевіркою умови (3), або з використанням спеціальних методів, наприклад, методу послідовних поступок, вагового методу, методу робочих характеристик. Вибір відповідного методу оптимізації залежить від змісту сформульованих вихідних даних, типу поставленої задачі проектування. Розглянемо особливості деяких методів.
Метод перебору. При розв'язанні
оптимізаційної задачі методом перебору згідно з умовою (3) припускається, що множина ![]() має
скінченну потужність. Такі задачі виникають, наприклад, при виборі з уже
відомих (“у натурі” або у вигляді технічних проектів) варіантів систем.
Зокрема, множина допустимих систем може формуватися на основі відомого
морфологічного підходу як різні допустимі комбінації певної кількості
підсистем. Тут суттєво зазначити, що навіть для порівняно простих систем, які
складаються лише з кількох підсистем, кількість допустимих комбінацій останніх
може бути значною (десятки і сотні тисяч). Тому, хоча принципових труднощів при
використанні методу перебору не існує, проте на практиці можливі складнощі
обчислювального характеру.
має
скінченну потужність. Такі задачі виникають, наприклад, при виборі з уже
відомих (“у натурі” або у вигляді технічних проектів) варіантів систем.
Зокрема, множина допустимих систем може формуватися на основі відомого
морфологічного підходу як різні допустимі комбінації певної кількості
підсистем. Тут суттєво зазначити, що навіть для порівняно простих систем, які
складаються лише з кількох підсистем, кількість допустимих комбінацій останніх
може бути значною (десятки і сотні тисяч). Тому, хоча принципових труднощів при
використанні методу перебору не існує, проте на практиці можливі складнощі
обчислювального характеру.
Метод робочих характеристик. Метод полягає у тому, що шукається оптимум однієї із цільових, наприклад, першої функції на множині строго допустимих систем при умові, що на всі цільові функції накладаються обмеження типу рівності
![]() , при
, при ![]() , (5)
, (5)
де ![]() - фіксовані, але довільні значення показників якості.
- фіксовані, але довільні значення показників якості.
Очевидно, оптимальне значення показника ![]() у
загальному випадку залежатиме від фіксованих значень інших показників якості
у
загальному випадку залежатиме від фіксованих значень інших показників якості ![]() . Знайдені у такий спосіб
залежності за допустимих комбінацій фіксованих значень
. Знайдені у такий спосіб
залежності за допустимих комбінацій фіксованих значень ![]() у критеріальному просторі являють собою
робочу поверхню. Робочій поверхні відповідає сім'я одновимірних робочих
характеристик
у критеріальному просторі являють собою
робочу поверхню. Робочій поверхні відповідає сім'я одновимірних робочих
характеристик ![]() виду
виду
![]() ,
,
![]() , (6)
, (6)
...........................
![]() .
.
Тут підкреслені змінні, що розглядаються як фіксовані параметри.
Робоча поверхня має такі характерні властивості:
1. Робоча поверхня включає усі Парето-оптимальні точки, але поряд з ними має і ряд безумовно гірших точок. Вони мають бути відкинуті з подальшого розгляду.
Необхідною і достатньою умовою збіжності робочої поверхні з Парето-оптимальною множиною, є її строга монотонність, тобто монотонно спадний характер відносно кожного з аргументів. В цьому випадку робоча поверхня визначає БПХ системи.
Основні складнощі при використанні методу робочих характеристик полягають
у розв'язанні задачі скалярної оптимізації в умовах ![]() -го
обмеження типу рівностей. Але у багатьох практичних випадках таку задачу
вдається довести до одержання конкретної структури системи з довільними
параметрами.
-го
обмеження типу рівностей. Але у багатьох практичних випадках таку задачу
вдається довести до одержання конкретної структури системи з довільними
параметрами.
Ваговий метод. При його застосуванні Парето-оптимальні рішення знаходяться шляхом оптимізації зваженої суми цільових функцій виду
![]() . (7)
. (7)
Тут ![]() — скінченні додаткові зважуючі коефіцієнти. При цьому знаходиться
оптимальне значення
— скінченні додаткові зважуючі коефіцієнти. При цьому знаходиться
оптимальне значення ![]() і відповідні
йому значення показників якості
і відповідні
йому значення показників якості ![]() ,
,
![]() . (8)
. (8)
У загальному випадку значення ![]() залежать
від обраних вагових коефіцієнтів
залежать
від обраних вагових коефіцієнтів ![]() :
:
![]() ,
,
![]() ,
,
….…...................... (9)
![]() .
.
Для розв'язання оптимізаційної задачі (7), а також для знаходження залежностей (9) необхідно виконати оптимізацію для всіх можливих комбінацій коефіцієнтів
![]() .
.
Розв'язавши систему із ![]() рівнянь
(9) можна дістати залежність
рівнянь
(9) можна дістати залежність
![]() . (10)
. (10)
У ![]() -вимірному просторі
векторних оцінок ця залежність розглядається, як рівняння вагової поверхні.
Неважко бачити, що використання вагового методу зводиться до скалярної
оптимізації, зокрема, відомим методом множників Лагранжа.
-вимірному просторі
векторних оцінок ця залежність розглядається, як рівняння вагової поверхні.
Неважко бачити, що використання вагового методу зводиться до скалярної
оптимізації, зокрема, відомим методом множників Лагранжа.
Вагова поверхня має такі властивості:
1. Включає тільки Парето-оптимальні точки, тобто жодна з безумовно гірших точок не може належати цій поверхні.
У багатьох випадках вагова поверхня є повністю визначеною і неперервною в
усьому діапазоні значень показників якості ![]() .
У таких випадках вагова поверхня збігається з Парето оптимальною множиною.
.
У таких випадках вагова поверхня збігається з Парето оптимальною множиною.
Отже, при використанні розглянутих методів, а також їхніх модифікацій векторна оптимізаційна задача зводиться у математичному відношенні до розв'язання множини скалярних оптимізаційних задач з урахуванням різного роду обмежень.
У загальному випадку при розв'язанні оптимізаційних задач (5), (7) варіюється оператор системи ![]() , тобто як структура
, тобто як структура ![]() , так і параметри
, так і параметри ![]() системи. При цьому
можуть бути використані методи варіаційного числення, функціонального аналізу,
теорії статистичних рішень, теорії інформації. При фіксованій структурі системи
системи. При цьому
можуть бути використані методи варіаційного числення, функціонального аналізу,
теорії статистичних рішень, теорії інформації. При фіксованій структурі системи ![]() задача синтезу зводиться до задачі
оптимізації вектора параметрів
задача синтезу зводиться до задачі
оптимізації вектора параметрів ![]() .
Ця задача у ряді випадків може розв'язуватися методами лінійного, нелінійного
чи динамічного програмування.
.
Ця задача у ряді випадків може розв'язуватися методами лінійного, нелінійного
чи динамічного програмування.
Якщо знайдена множина Парето ![]() порівняно
вузька, то за оптимальне рішення може бути прийнята люба Парето-оптимальна
оцінка і відповідна їй система. У таких випадках можна вважати, що відношення
строгої переваги
порівняно
вузька, то за оптимальне рішення може бути прийнята люба Парето-оптимальна
оцінка і відповідна їй система. У таких випадках можна вважати, що відношення
строгої переваги ![]() збігається з відношенням
збігається з відношенням ![]() на множині векторних
оцінок, а тому
на множині векторних
оцінок, а тому ![]() . При цьому
часто і не вдаються до пошуку всієї множини Парето-оптимальних систем, а зразу
вибирають один із Парето-оптимальних варіантів.
. При цьому
часто і не вдаються до пошуку всієї множини Парето-оптимальних систем, а зразу
вибирають один із Парето-оптимальних варіантів.
Проте часто множина ![]() є
занадто обширною. Це свідчить, що відношення
є
занадто обширною. Це свідчить, що відношення ![]() та
та ![]() хоча
і зв'язані аксіомою Парето, але не збігаються. Для звуження множини
Парето-оптимальних оцінок слід використати умовний критерій переваги (УПК),
який зводиться до задання деякої скалярної цільової функції. УКП може бути
заданий після одержання додаткової інформації та введенні різного роду умов.
хоча
і зв'язані аксіомою Парето, але не збігаються. Для звуження множини
Парето-оптимальних оцінок слід використати умовний критерій переваги (УПК),
який зводиться до задання деякої скалярної цільової функції. УКП може бути
заданий після одержання додаткової інформації та введенні різного роду умов.
При цьому постає запитання: чи має сенс виконувати синтез на основі безумовного критерію переваги - критерію Парето, якщо на заключному етапі все ж доводиться вводити умовний критерій переваги. В обґрунтування доцільності пошуку Парето-оптимальних варіантів систем з використанням БКП на початкових етапах оптимального проектування зазначимо таке:
1. БКП дає змогу знайти всі Парето-оптимальні системи, тобто відкинути безумовно гірші варіанти системи.
БКП дає змогу знайти потенціальні (найкращі можливі) значення кожного із показників якості і зв'язок між ними.
3. Методи відшукання Парето-оптимальних систем зводяться у математичному відношенні до оптимізації скалярних цільових функцій, тобто зводять розв'язання задачі векторного синтезу до деякої множини задач скалярного синтезу.
4. У виродженому випадку БКП дає змогу знайти єдину найкращу систему.
5. У невиродженому випадку знаходження Парето-оптимальних систем часто приводить до однієї структури системи, але з різними параметрами.
6. Навіть тоді, коли на заключному етапі синтезу для вибору єдиної системи доводиться вводити УКП, то краще вводити різного роду умовності на більш пізньому етапі синтезу.
5 Методи звуження множини Парето-оптимальних рішень
Формальна модель задачі Парето-оптимізації не містить інформації для
вибору єдиної альтернативи. При цьому множина допустимих варіантів системи лише
звужується до множини Парето шляхом виключення безумовно гірших варіантів за
відношенням ![]() . Проте для наступних етапів проектування
системи, як правило, має бути обраний єдиний варіант системи. Тому виникає
необхідність звуження множини Парето-оптимальних рішень із залученням
додаткової інформації про відношення
. Проте для наступних етапів проектування
системи, як правило, має бути обраний єдиний варіант системи. Тому виникає
необхідність звуження множини Парето-оптимальних рішень із залученням
додаткової інформації про відношення ![]() . Така інформація з'являється в результаті різностороннього аналізу
структури і параметрів Парето-оптимальних варіантів системи, багатовимірних
діаграм обміну показників якості системи, відносної важливості показників
якості, порівняльного аналізу одержаних варіантів системи між собою.
. Така інформація з'являється в результаті різностороннього аналізу
структури і параметрів Парето-оптимальних варіантів системи, багатовимірних
діаграм обміну показників якості системи, відносної важливості показників
якості, порівняльного аналізу одержаних варіантів системи між собою.
Отримана при цьому додаткова інформація може бути використана для
побудови скалярної цільової функції ![]() , оптимізація якої на множині Парето-оптимальних рішень
, оптимізація якої на множині Парето-оптимальних рішень ![]() приводить до вибору
єдиного оптимального варіанта системи
приводить до вибору
єдиного оптимального варіанта системи
![]() . (11)
. (11)
Загальна вимога до функції ![]() зводиться
до того, щоб вона була монотонною (зростаючою чи спадною) по кожному зі своїх
аргументів.
зводиться
до того, щоб вона була монотонною (зростаючою чи спадною) по кожному зі своїх
аргументів.
Існують як об'єктивні, так і суб'єктивні підходи до побудови такої
функції. У ряді випадків на основі розгляду призначення системи, що
проектується у складі більш складної надсистеми (комплексу), об'єктивними
методами може бути встановлено взаємозв'язок показників якості системи ![]() з якимось показником
якості
з якимось показником
якості ![]() надсистеми у вигляді
відповідної функції
надсистеми у вигляді
відповідної функції ![]() . Проте у
більшості випадків об'єктивно ввести таку функцію не вдається і доводиться
вдаватись до її побудови значною мірою суб'єктивними методами. Розглянемо деякі
з них.
. Проте у
більшості випадків об'єктивно ввести таку функцію не вдається і доводиться
вдаватись до її побудови значною мірою суб'єктивними методами. Розглянемо деякі
з них.
Вибір оптимальних рішень з використанням функцій цінності. Одним із широко використовуваних методів звуження
множини Парето-оптимальних рішень є використання скалярної функції цінності
(корисності), оптимізація якої веде до вибору одного з оптимальних варіантів
системи. Числову функцію ![]() називають
функцією цінності для відношення строгої переваги
називають
функцією цінності для відношення строгої переваги ![]() , якщо для довільних оцінок
, якщо для довільних оцінок ![]() ,
, ![]() у просторі
у просторі ![]() нерівність
нерівність ![]() має
місце тоді і тільки тоді, коли
має
місце тоді і тільки тоді, коли ![]() . Припустимо, що відношення строгої переваги
. Припустимо, що відношення строгої переваги ![]() задовольняє аксіому Парето. При цьому із
нерівності
задовольняє аксіому Парето. При цьому із
нерівності ![]() випливає відношення
випливає відношення ![]() , що означає
, що означає ![]() ,
тобто функція цінності
,
тобто функція цінності ![]() , є зростаючою за
відношенням
, є зростаючою за
відношенням ![]() . Якщо існує функція
цінності
. Якщо існує функція
цінності ![]() , то оптимальна оцінка знаходиться шляхом максимізації цієї функції на
множині Парето
, то оптимальна оцінка знаходиться шляхом максимізації цієї функції на
множині Парето
![]() . (12)
. (12)
Тобто відшукання оптимальної оцінки зводиться до розв'язання задачі
скалярної оптимізації функції багатьох змінних ![]() .
.
При цьому можуть бути побудовані адитивна, мультиплікативна, полінійна функції цінності.
Процедура утворення функції
цінності ![]() інколи
називається згорткою векторного критерію
інколи
називається згорткою векторного критерію ![]() .
.
Операція згортки можлива, якщо:
- частинні критерії кількісно
сумарні по важливості, тобто кожному з них відповідає певне число ![]() , яке визначає його
відносну важливість відповідно до інших критеріїв;
, яке визначає його
відносну важливість відповідно до інших критеріїв;
- частинні критерії є однорідні, тобто кількісно порівнюються в одній вимірності.
Існують різноманітні форми подання узагальненого скалярного критерію та вибору відповідних оптимальних рішень. Зокрема, це такі способи згортки частинних критеріїв:
- формується узагальнений критерій, чисельник якого складає добуток критеріїв, які підлягають максимізації, а знаменник - добуток критеріїв, які підлягають мінімізації;
- формується узагальнений критерій з використання елементів теорії адитивної корисності, тобто підсумовування частинних критеріїв за певною вагою коефіцієнтів вибору чисельника і знаменника;
- формується узагальнений критерій відносно всіх частинних критеріїв.
Узагальнена функція цінності може набирати такого вигляду
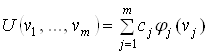 , (13)
, (13)
де ![]() - одновимірні функції цінності, що характеризують цінність системи за
- одновимірні функції цінності, що характеризують цінність системи за ![]() -м показником якості;
-м показником якості; ![]() - шкалюючі коефіцієнти.
- шкалюючі коефіцієнти.
Задача побудови функції
(13) зводиться до оцінки
коефіцієнтів ![]() , вибору виду функцій
, вибору виду функцій ![]() , перевірки їх незалежності
за перевагою
, перевірки їх незалежності
за перевагою ![]() , перевірки узгодженості побудованої функції цінності. У ряді випадків може бути використана функція цінності (13) у вигляді
, перевірки узгодженості побудованої функції цінності. У ряді випадків може бути використана функція цінності (13) у вигляді
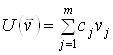 . (14)
. (14)
При цьому використовуються різні методи одержання додаткової інформації
про значення коефіцієнтів ![]() .
Зокрема, це добре розроблені методи експертних оцінок. Вони зводяться до опитування вибраної групи експертів про цінність
одержаних Парето-оптимальних варіантів системи, відносну важливість показників
якості та інше. Існують добре розроблені методики врахування одержаної
інформації, які реалізовані у методі Сааті.
.
Зокрема, це добре розроблені методи експертних оцінок. Вони зводяться до опитування вибраної групи експертів про цінність
одержаних Парето-оптимальних варіантів системи, відносну важливість показників
якості та інше. Існують добре розроблені методики врахування одержаної
інформації, які реалізовані у методі Сааті.
Інколи для вибору єдиного варіанту обмежуються так званою пороговою оптимізацією: найбільш вагомий критерій піддається оптимізації, інші включаються до системи обмежень. Слід зауважити, що існує також багато інших принципів та підходів до вибору єдиного варіанту з використанням скалярних критеріїв оптимальності. Фактично співвідношення (14) визначає байесовий детермінований критерій оптимальності. За умов невизначеності про умови вибору рішень використовує методи теорії ігор. Такі ситуації вибору проектних рішень при створенні систем часто називають «іграми з природою». Для прийняття рішень вишукують найкращу стратегію, з використанням критерія Вальда, критерія Севіджа, критерія Гурвіца, критерія Лапласа та інших.
Вибір оптимальних рішень на основі теорії розмитих множин. Цей підхід базується на тому, що через
апріорну невизначеність поняття «найкращий варіант системи» неможливо визначити
точно. Можна вважати, що це поняття являє собою розмиту множину і для оцінки
системи можуть бути використані основні положення теорії розмитих множин. У загальному випадку розмита
множина ![]() на множині
на множині ![]() задається функцією
належності
задається функцією
належності ![]() :
: ![]() , яка зіставляє з кожним елементом
, яка зіставляє з кожним елементом ![]() дійсне
число
дійсне
число ![]() на інтервалі
на інтервалі ![]() . Це число називається ступенем належності
елемента
. Це число називається ступенем належності
елемента ![]() розмитій множині
розмитій множині ![]() . Чим воно ближче до
. Чим воно ближче до ![]() , тим вищий ступінь належності. Функція
, тим вищий ступінь належності. Функція ![]() є узагальненням
характеристичної функції множин, яка набуває лише два значення:
є узагальненням
характеристичної функції множин, яка набуває лише два значення: ![]() - при
- при ![]() і
і ![]() - при
- при ![]() .
У випадку дискретних множин використовується запис розмитої множини як множини
пар
.
У випадку дискретних множин використовується запис розмитої множини як множини
пар ![]() .
.
Згідно з цими основними положеннями кожний показник якості системи може
задаватися у вигляді розмитої множини ![]() ,
де
,
де ![]() - функція належності конкретного
- функція належності конкретного ![]() -го
показника якості розмитій множині найкращого значення.
-го
показника якості розмитій множині найкращого значення.
Такий запис окремого показника якості має високу інформативність, оскільки дає уяву про фізичну природу показника якості, конкретне його значення і цінність відносно найкращого (екстремального) значення, що характеризує функція належності. Універсальна форма функції належності, яка може бути використана як скалярна цільова функція, має такий вид
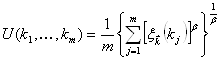 . (15)
. (15)
Перевагою такої цільової функції є те, що вибором параметра ![]() може бути реалізовано широкий клас
функцій від лінійної адитивної за умови
може бути реалізовано широкий клас
функцій від лінійної адитивної за умови ![]() , до сугубо нелінійної при
, до сугубо нелінійної при ![]() .
.
Вибір оптимального варіанту при строго впорядкованих за важливістю
показниках якості.
Інколи для замовника
системи за результатами аналізу Парето-оптимальних варіантів, а також їх БДО
виявляється бажаним одержати якомога більше значення одного з показників
якості, наприклад ![]() , навіть за
рахунок погіршення інших показників якості. Це означає, що показник
, навіть за
рахунок погіршення інших показників якості. Це означає, що показник ![]() є важливішим порівняно з
іншими показниками якості.
є важливішим порівняно з
іншими показниками якості.
Можливий також випадок, коли весь набір показників якості ![]() , строго упорядкований за
важливістю, тобто показник
, строго упорядкований за
важливістю, тобто показник ![]() більш
важливий, ніж показники
більш
важливий, ніж показники ![]() ,
показник
,
показник ![]() більш важливий, ніж показники
більш важливий, ніж показники ![]() і т.д.
Цьому відповідає ситуація, коли при порівнянні оцінок систем використовується
лексикографічне відношення. Наведемо означення цього відношення та особливості
використання при виборі єдиного варіанту системи.
і т.д.
Цьому відповідає ситуація, коли при порівнянні оцінок систем використовується
лексикографічне відношення. Наведемо означення цього відношення та особливості
використання при виборі єдиного варіанту системи.
Нехай є два вектори оцінок ![]() ,
, ![]() . Лексикографічне
відношення
. Лексикографічне
відношення ![]() має місце тоді і тільки тоді, коли
виконується одна з таких умов
має місце тоді і тільки тоді, коли
виконується одна з таких умов
![]() ,
,
![]() , (16)
, (16)
............................
![]() .
.
Для ![]() лексикографічне відношення
збігається з відношенням
лексикографічне відношення
збігається з відношенням ![]() на
підмножині дійсних чисел. При виконанні відношення
на
підмножині дійсних чисел. При виконанні відношення ![]() кажуть, що вектор
кажуть, що вектор ![]() лексикографічно більший за вектор
лексикографічно більший за вектор ![]() .
.
Якщо використовується лексикографічне відношення при виборі єдиної
системи, то це означає, що із пари оцінок (і відповідних їм систем) перевага
віддається тій оцінці (системі), в якої перша
компонента вектора ![]() (тобто оцінка показника якості
(тобто оцінка показника якості ![]() ) більша, незалежно від
співвідношення по інших компонентах вектора. Якщо перші компоненти оцінок
однакові, то перевага віддається тій оцінці (системі), в якої більша друга
компонента вектора
) більша, незалежно від
співвідношення по інших компонентах вектора. Якщо перші компоненти оцінок
однакові, то перевага віддається тій оцінці (системі), в якої більша друга
компонента вектора ![]() (оцінка показника якості
(оцінка показника якості ![]() ). Наступні компонентам вектора
). Наступні компонентам вектора ![]() можуть при цьому
значно програвати відповідним компонентам вектора
можуть при цьому
значно програвати відповідним компонентам вектора ![]() .
.
Аналогічні висновки мають місце при рівності перших двох компонент, трьох
компонент і так далі до ![]() компонент
векторів
компонент
векторів ![]() і
і ![]() . У таких
випадках стверджують, що компоненти
. У таких
випадках стверджують, що компоненти ![]() , тобто
оцінки показників якості системи
, тобто
оцінки показників якості системи ![]() строго
упорядковані за важливістю.
строго
упорядковані за важливістю.
У визначенні лексикографічного відношення важливу роль відіграє порядок перерахування показників якості. Зміна нумерації показників якості приводить до другого лексикографічного відношення. Крім згаданих вище методів побудови скалярної цільової функції і вибору варіанта з множини Парето-оптимальних, існує і багато інших. Вибір підходящого методу визначається вихідними даними та типом конкретної оптимізаційної задачі. Але якби-то не було, оптимальні варіанти системи слід шукати серед Парето-оптимальних розв'язків задачі. Тобто етап Парето-оптимізації є обов'язковим при проектуванні систем з урахуванням сукупності показників якості.