Контрольная работа: Уравнения, содержащие параметр
Городская конференция учащихся муниципальных образовательных учреждений, занимающихся учебно-воспитательной деятельностью
«Шаги в науку»
Научное общество учащихся «Поиск»
Муниципального образовательного учреждения
«Средняя общеобразовательная школа №86 г.Омска»
Научное направление: «Математика»
Уравнения, содержащие параметр
Соколова Александра Михайловна
ученица 10 класса МОУ
«СОШ №86 г.Омска»
Руководитель: Дощанова Тиштых Мухановна,
учитель математики
Омск 2011
Содержание
Введение
1. Знакомство с параметрами
1.1 Решение уравнений первой степени с одним неизвестным
1.2 Решение линейных уравнений с модулем
1.3 Решение квадратных уравнений
2. Примеры решений уравнений с параметром из ГИА и ЕГЭ части С
Заключение
Введение
В настоящее время различные задачи с параметрами – это одни из самых сложных заданий на экзаменах. А ведь в экзаменационных заданиях они есть как за 9 класс, так и за 11, но многие ученики даже не берутся решать эти задания, так как заведомо считают, что не смогут их решить, даже не попробовав. А на деле, чтобы справиться с ними, нужно всего лишь проявить логику, включить смекалку и ничего сложного не окажется.
Свою работу я захотела посвятить заданиям с параметрами, так как именно они вызывают у большинства учеников наибольшие затруднения. Мне самой нужно будет сдавать ЕГЭ, и поэтому, обращаясь к этой теме, я хотела бы облегчить и себе, и своим слушателям, тяжесть решения задач с параметрами.
Цель моей работы - научиться решать уравнения с параметрами и познакомить учеников с методами решения подобных заданий.
Я поставила перед собой следующие задачи:
1. Самой научиться решать уравнения с параметрами различных видов.
2. Познакомить учащихся с разными методами решения подобных уравнений.
3. Вызвать интерес учеников к дальнейшему изучению задач с параметрами.
В моей работе я рассмотрю следующие виды заданий с параметрами:
1) решение уравнений первой степени с одним неизвестным;
2) решение линейных уравнений с модулем;
3) решение квадратных уравнений.
уравнение параметр неизвестное модуль
1. Знакомство с параметрами
Для начала, стоило бы пояснить, что собой представляют уравнения с параметрами, которым посвящена моя работа. Итак, если уравнение (или неравенство), кроме неизвестных, содержит числа, обозначенные буквами, то оно называется параметрическим, а эти буквы – параметрами.
Если параметру, содержащемуся в уравнении (неравенстве), придать некоторое значение, то возможен один из двух следующих случаев:
1) получится уравнение (неравенство), содержащее лишь данные числа и неизвестные (т.е. без параметров);
2) получится условие, лишенное смысла.
В первом случае значение
параметра считается допустимым, во втором – недопустимым. ![]()
Решить уравнение (неравенство), содержащее параметр, - это значит, для каждого допустимого значения параметра найти множество всех значений данного уравнения (неравенства).
К сожалению, не редко при
решении примеров с параметрами многие ограничиваются тем, что составляют
формулы, выражающие значения неизвестных через параметры. Например, при решении
уравнения ![]() переходят к у равнению
переходят к у равнению ![]() ; при m=
; при m=![]() записывают единственное решение
записывают единственное решение 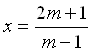 . Но ведь при m= -1 – бесчисленное множество
решений, а при m=1, решений нет.
. Но ведь при m= -1 – бесчисленное множество
решений, а при m=1, решений нет.
Пример 1. Решить
уравнение ![]() .
.
Сразу видно, что при решении этого уравнения стоит рассмотреть следующие случаи:
1) a=1, тогда уравнение принимает вид ![]() и не имеет решений;
и не имеет решений;
2) при а=-1 получаем ![]() и, очевидно, х любое;
и, очевидно, х любое;
3) при ![]()
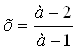 .
.
Ответ: при a=1 решений нет, при а=-1 х любое, при
![]()
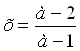 .
.
Пример 2. Решить
уравнение ![]()
Очевидно, что ![]() , а
, а ![]() , то есть х=b/2, но
, то есть х=b/2, но ![]() ,
то есть 2
,
то есть 2![]() b/2, b
b/2, b![]() 4.
4.
Ответ: при b![]() 4 х=b/2; при b=4 нет
решений.
4 х=b/2; при b=4 нет
решений.
Пример 3. При каких а
уравнение ![]() имеет единственное
решение?
имеет единственное
решение?
Сразу хочу обратить
внимание на распространенную ошибку – считать данное уравнение квадратным. На
самом деле это уравнение степени не выше второй! При а – 2=0, а = 2, уравнение
вырождается в линейное имеет единственный корень х=1/4. Если же а![]() 2, то мы действительно
имеем дело с квадратным уравнением, которое даёт единственное решение при D=0
2, то мы действительно
имеем дело с квадратным уравнением, которое даёт единственное решение при D=0 ![]() ,
,
![]() , а=1, а=6.
, а=1, а=6.
Ответ: при а=2, а=1, а=6.
1.1 Решение уравнений первой степени с одним неизвестным
Решить такое уравнение – это значит:
1) определить множество допустимых значений неизвестного и параметров;
2) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнений.
Простейшее уравнение первой степени с одним неизвестным имеет вид ах-b=0.
![]()
![]()
![]()
![]()
![]() При
При ![]() уравнение
имеет единственное решение
уравнение
имеет единственное решение 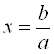 ,
которое будет: положительным, если
,
которое будет: положительным, если 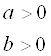 или
или ![]() ; нулевым, если
; нулевым, если ![]() ; отрицательным, если
; отрицательным, если 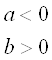 или
или ![]() .
.
Если а=0, то при b=0 бесчисленное множество решений, а
при b![]() 0 решений нет.
0 решений нет.
Пример 1. Для каждого
значения а решить уравнение ![]() ; найти
при каких а корни больше нуля.
; найти
при каких а корни больше нуля.
Это уравнение не является
линейным уравнением (т.е. представляет собой дробь), но при х![]() -1 и х
-1 и х![]() 0 сводится к таковому:
0 сводится к таковому: ![]() или а-1-х=0.
или а-1-х=0.
Мы уже выявили допустимые
значения икс (х![]() -1 и х
-1 и х![]() 0), выявим теперь
допустимые значения параметра а:
0), выявим теперь
допустимые значения параметра а:
а-1-х=0 ![]() а=х+1
а=х+1
Из этого видно, что при х![]() 0 а
0 а![]() 1, а при х
1, а при х![]() -1 а
-1 а![]() 0.
0.
Таким образом, при а![]() 1 и а
1 и а![]() 0 х=а-1 и это корень
больше нуля при а>1.
0 х=а-1 и это корень
больше нуля при а>1.
Ответ: при а<0 х=а-1;
при ![]() решений нет, а при a>1 корни положительны.
решений нет, а при a>1 корни положительны.
Пример 2. Решить
уравнение ![]() (1).
(1).
Допустимыми значениями k и x будут значения, при которых ![]()
![]() .
.
Приведём уравнение к простейшему виду:
9х-3k=kx-12
(9 – k)x =3k-12 (2)
Найдём k, при которых изначальное уравнение не имеет смысла:
Подставив в (2) ![]() , получим:
, получим:
![]() .
.
Если подставим ![]() , то получим так же
, то получим так же ![]() .
.
Таким образом, при ![]() уравнение (1) не имеет
числового смысла, т.е.
уравнение (1) не имеет
числового смысла, т.е. ![]() - это
недопустимые значения параметра k для
(1). При
- это
недопустимые значения параметра k для
(1). При ![]() мы можем решать только
уравнение (2).
мы можем решать только
уравнение (2).
1.
Если ![]() , то уравнение (2) и вместе
с ним уравнение (1) имеют единственное решение
, то уравнение (2) и вместе
с ним уравнение (1) имеют единственное решение ![]() ,
которое будет:
,
которое будет:
а) положительным, если ![]() , при 4<k<9, с учётом
, при 4<k<9, с учётом ![]() :
: ![]() ;
;
б) нулевым, если ![]() ;
;
в) отрицательным, если ![]() и k>9 с учётом
и k>9 с учётом
![]() , получаем
, получаем ![]() .
.
2.
Если ![]() , то уравнение (2) решений
не имеет.
, то уравнение (2) решений
не имеет.
Ответ: а) ![]() при
при ![]() и
и ![]() , причём х>0 для
, причём х>0 для ![]() ; x=0 при k=4; x<0 при
; x=0 при k=4; x<0 при ![]() ;
;
б) при ![]() уравнение не имеет решений.
уравнение не имеет решений.
1.2 Решение линейных уравнений с модулем
Для начала, стоит вспомнить, что такое модуль числа. Итак, абсолютной величиной или модулем числа называется само число х, если х положителен, число (-х), если х отрицателен, или нуль, если х=0. Значение модуля может быть только положительным.
Чтобы понять решение параметрических уравнений, содержащих знак модуля, лучше всего продемонстрировать решение наглядно, т.е. привести примеры:
Пример 1. Решить уравнение |x-2|=b.
Так как, по определению
модуля, |x-2|![]() ,
то при b<0 данное уравнение решений не
имеет. Если b=0, то уравнение имеет решение х=2.
,
то при b<0 данное уравнение решений не
имеет. Если b=0, то уравнение имеет решение х=2.
Если b>0, то решениями уравнения являются числа x=2+b и x=2-b.
Ответ: при b<0 решений нет, при b=0 х=2, при b>0 х=2+b и x=2-b.
Пример 2. Решить уравнение |x-a|=|x-4|. Удобнее всего данное уравнение решить методом интервалов, для двух случаев:
1) a![]() ;
;
2) 4![]() .
.
1. Первый интервал:
![]()
![]()
![]()
![]()
![]() ;
;
Второй интервал:
![]()
![]()
![]()

![]() , т.е. если а<4, то
, т.е. если а<4, то ![]() .
.
Третий интервал:
![]()
![]() а=4, т.е. если а=4,
то
а=4, т.е. если а=4,
то ![]() .
.
2. Первый интервал:
![]()
 а=4,
а=4, ![]() .
.
![]() Второй интервал:
Второй интервал:
![]()
![]()

![]() a>4,т.е. если 4<а, то
a>4,т.е. если 4<а, то ![]()
Третий интервал:
![]()
![]()
![]()
![]()
![]()
Ответ: при а=4 х-любое;,
при а<4 ![]() .
.
Пример 3. Для каждого значения параметра а найти все значения х, удовлетворяющие уравнению |x+3|– a| x – 1| =4.
Рассмотрим 3 промежутка:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() и решим исходное уравнение
на каждом промежутке.
и решим исходное уравнение
на каждом промежутке.
1. ![]() ,
, ![]() .
.
При а=1 уравнение не
имеет решений, но при а![]() 1 уравнение имеет
корень
1 уравнение имеет
корень ![]() . Теперь надо выяснить, при
каких а х попадает на промежуток x<
– 3, т.е.
. Теперь надо выяснить, при
каких а х попадает на промежуток x<
– 3, т.е. ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Следовательно, исходное
уравнение на x< – 3 имеет один корень
. Следовательно, исходное
уравнение на x< – 3 имеет один корень ![]() при
при ![]() , а на остальных а корней
не имеет.
, а на остальных а корней
не имеет.
2. ![]() .
. ![]() .
.
При а= – 1 решением
уравнения является любое х; но мы решаем на промежутке ![]() . Если а
. Если а![]() 1, то уравнение имеет один
корень х=1.
1, то уравнение имеет один
корень х=1.
3. ![]() .
. ![]() .
.
При а=1 решением является
любое число, но мы решаем на ![]() . Если а
. Если а![]() 1, то х=1.
1, то х=1.
Ответ: при ![]()
![]() ; при а= – 1
; при а= – 1 ![]() и при а
и при а![]() 1 х=1; при а=1
1 х=1; при а=1 ![]() и при а
и при а![]() 1 х=1.
1 х=1.
1.3 Решение квадратных уравнений с параметром
Для начала напомню, что
квадратное уравнение – это уравнение вида ![]() ,
где а, b и с – числа, причем, а
,
где а, b и с – числа, причем, а![]() 0.
0.
Условия параметрических
квадратных уравнений могут быть различны, но для решений всех их нужно
применять свойства обыкновенного квадратного уравнения ![]() :
:
а) Если D>0, а>0, то уравнение имеет два действительных различных корня, знаки которых при с>0 одинаковые и противоположны по знаку коэффициента b, а при с<0, причем по абсолютной величине больше тот, знак которого противоположен коэффициенту b.
б) Если D=0, а>0, то уравнение имеет два действительных и равных между собой корня, знак которых противоположен знаку коэффициента b.
в) Если D<0, а>0, то уравнение не имеет действительных корней.
Аналогично можно представить свойства корней при а<0. Кроме того, в квадратных уравнениях справедливы следующие утверждения:
1. Если поменять местами коэффициенты а и с, то корни полученного квадратного уравнения будут обратны корням данного.
2. Если поменять знак коэффициента b, корни полученного квадратного уравнения будут противоположны корням данного.
3. Если коэффициенты а и с разных знаков, то уравнение имеет действительные корни.
Пример1. Найти все
значения параметра а, для которых квадратное уравнение ![]() : а) имеет два различных
корня; б) не имеет корней; в) имеет два равных корня.
: а) имеет два различных
корня; б) не имеет корней; в) имеет два равных корня.
Данное уравнение по
условию является квадратным, поэтому а![]() -1.
Рассмотрим дискриминант данного уравнения:
-1.
Рассмотрим дискриминант данного уравнения:
![]()
При а>-1 уравнение имеет два различных корня, т.к. D>0, при a<-1 уравнение корней не имеет, т.к. D<0, а двух одинаковых корней это уравнение иметь не может, т.к. D=0 при а=-1, а это противоречит условию задачи.
Пример2. Решить уравнение
![]()
При а=0 уравнение
является линейным 2х+1=0, которое имеет единственное решение х=-0.5. А при а![]() 0, уравнение является
квадратным и его дискриминант D=4-4a.
0, уравнение является
квадратным и его дискриминант D=4-4a.
При а>1 D<0 поэтому уравнение корней не
имеет. При а=1 D=0, поэтому
уравнение имеет два совпадающих корня ![]() =-1.
=-1.
При a<1, но а![]() 0, D>0 и данное уравнение имеет два различных корня
0, D>0 и данное уравнение имеет два различных корня
![]() ;
; ![]() .
.
Ответ: ![]() и
и ![]() при a<1, но а
при a<1, но а![]() 0; х=-0.5 при а=0;
0; х=-0.5 при а=0; ![]() =-1 при а=1.
=-1 при а=1.
Пример3. Корни уравнения ![]() таковы, что
таковы, что ![]() . Найдите а.
. Найдите а.
По теореме Виета ![]() и
и ![]() . Возведём обе части
первого равенства в квадрат:
. Возведём обе части
первого равенства в квадрат: ![]() .
Учитывая, что
.
Учитывая, что ![]() , а
, а ![]() , получаем:
, получаем: ![]() или
или ![]() ,
, ![]()
![]() . Проверка показывает, что
все значения
. Проверка показывает, что
все значения ![]() удовлетворяют условию.
удовлетворяют условию.
Ответ: ![]()
2. Примеры решений уравнений с параметром из ГИА и ЕГЭ части С
Узнав всю теоретическую основу и методы решений различных уравнений, содержащих параметр, я решила применить свои знания на практике. Мы выбрали несколько вариантов заданий ГИА и ЕГЭ из части С, представляющих собой именно те виды уравнений, которые были представлены в моей работе, а именно: уравнение первой степени с одним неизвестным, уравнение с модулем и квадратное уравнение. Ниже будут предложены решения этих уравнений.
1. Определить значения k, при которых корни уравнения ![]() положительны.
положительны.
Сразу можно выделить, что
![]() ,
, ![]() , из этого следует, что при
, из этого следует, что при
![]() уравнение не имеет смысла.
уравнение не имеет смысла.
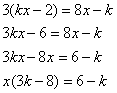
В уравнение х(3k-8)=6-k подставим недопустимые значения х, чтобы узнать, при каких k уравнение не имеет смысла:
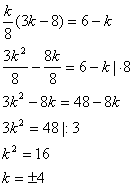
Итак, мы выяснили, что ![]() .
.
Выразим х: ![]() . Х будет больше нуля, если
. Х будет больше нуля, если
![]() .
.
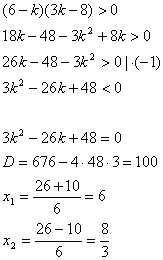
Учитывая, что ![]() ,
, ![]() ,
, ![]() . Ответ:
. Ответ: ![]() ,
, ![]() .
.
2. При каких значениях а
уравнение ![]() имеет равные корни?
имеет равные корни?
Уравнение имеет равные корни в том случае, если дискриминант равен нулю. Найдем дискриминант данного уравнения и приравняем его к нулю:
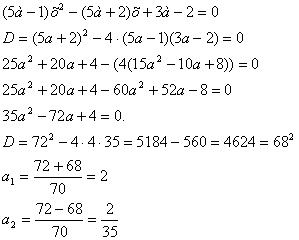
Ответ: при а=2 и а=2/35.
3. Для каждого значения параметра а найти все значения х, удовлетворяющие уравнению a|x+3|+2|x+4|=2.
1) х+3=0 2) х+4=0
х= – 3 х= – 4 .
х+3 – – +
![]()
х+4 – -4 + -3 +
Рассмотрим 3 промежутка.
1. ![]()
а(-(х+3)+2(-(х+4)=2
-ах – 3а –2х – 8=2
х(- а – 2)=10+3а (при а![]() - 2)
- 2)
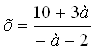 .
.
Теперь надо выяснить, при
каких а х попадает на промежуток ![]() .
.
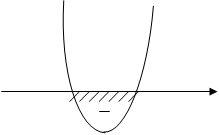
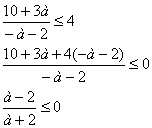
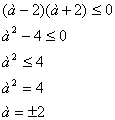
Следовательно, на
промежутке ![]() уравнение имеет
единственный корень
уравнение имеет
единственный корень ![]() при
при ![]() .
.
2. ![]() .
.
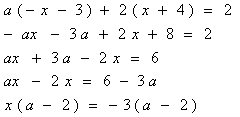
=> При а![]() 2 х= -3
2 х= -3
При а=2 ![]() .
.
3. ![]()
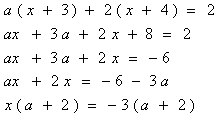
=> При а![]() -2 х= -3
-2 х= -3
При а= -2 ![]() .
.
Ответ: 1. при ![]()
![]()
2. при а![]() 2 х= -3
2 х= -3
при а=2 ![]() .
.
3. при а![]() -2 х= -3
-2 х= -3
при а= -2 ![]() .
.
Заключение
Итак, проделав эту работу, я действительно поняла, как решаются уравнения с параметрами, приобрела навык решения и, надеюсь, теперь не столкнусь с трудностями при решении подобных заданий на экзамене. Я надеюсь, что моя работа поможет ученикам успешнее и смелее решать различные задачи с параметрами.
Конечно, не все далось сразу и легко – чтобы научиться решать уравнения с параметрами, нужно выйти за рамки представлений об уравнении, при этом не забывая о свойствах того или иного типа уравнения. Удаётся это не сразу. К тому же, в школьной программе задачам с параметрами не уделяется должного внимания, поэтому, увидев такое на экзамене, конечно, можно растеряться. Но я надеюсь, что вызвала интерес учащихся к изучению таких интересных и нестандартных заданий, как уравнения, содержащие параметр.
| Самостоятельная работа как средство обучения решению уравнений в 5-9 ... | |
|
... РФ Светлоградский педагогический колледж Дипломная работа Самостоятельная работа как средство обучения решению уравнений в 5 - 9 классах Выполнила: Например, введение арифметического квадратного корня из рациональных чисел позволяет записывать корни не только уравнений вида х2 = b, где b-неотрицательное рациональное число, но ... Одна из важнейших таких связей - приложения методов, разрабатываемых в линии уравнений, к исследованию функции (например, к заданиям на нахождение области определения некоторых ... |
Раздел: Рефераты по педагогике Тип: реферат |
| Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ ... | |
|
Кольцом называется числ. множ. На котором выполняются три опер-ии: слож, умнож, вычит. Полем наз. Числ множ. На котором выполняются 4 операции: слож ... 2. Скал. произв. двух векторов равно произведению модуля одного из них на проекцию другого на направление третьего (a",b")=|a"|*прA" b" 3.Скалярное произ a" на сумму b"+c" равно ... x"=x1cos -Ey1sin +a y"=x1sin +Ey1cos +b рассмотрим произведение d*h: x"=k*xcos -Ek*ysin +a y"=k*xsin +Ek*ycos +b вынесем к и приведем к виду x"=k*(xcos -Eysin )+a y"=k(xsin +Eycos ... |
Раздел: Рефераты по математике Тип: реферат |
| Методы решения уравнений, содержащих параметр | |
|
Выпускная квалификационная работа Выполнил тудент V курса математического факультета Кузнецов Е.М. Вятский государственный гуманитарный университет ... При изучении темы "Квадратные уравнения" в разделе дополнительных упражнений для более углубленного повторения материала предлагаются уравнения, содержащие параметр (№№ 645, 646 ... Дело в том, что если дискриминант D=0 при а=ао, то при переходе значения D через точку ао дискриминант может изменить знак (например, при а<ао D < 0, а при а>ао D > 0). Вместе с ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| Комплексные числа (избранные задачи) | |
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ "ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ... ... для комплексных чисел в алгебраической форме, степень мнимой единицы, модуль комплексного числа, а также излагается правило извлечения квадратного корня из комплексного числа. Лучше сначала считать х параметром и решать квадратное относительно а уравнение , а затем поменять x и a ролями. |
Раздел: Рефераты по математике Тип: дипломная работа |
| Элективный курс по алгебре для 9-го класса на тему "Квадратные ... | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования "Вятский государственный ... К таким задачам относятся: задачи на применение теоремы Виета, на соотношения между корнями квадратного уравнения, на взаимное расположение корней квадратного уравнения, решение ... 5. Найдите все значения параметра k, при которых уравнение (k-2)x-2kx+2k-3=0 имеет хотя бы один корень? |
Раздел: Рефераты по педагогике Тип: дипломная работа |