Лабораторная работа: Математическое моделирование работы систем массового обслуживания
ЛАБОРАТОРНАЯ РАБОТА
Математическое моделирование работы систем массового обслуживания
Задание
Вариант 1. Газозаправочная станция для автомобилей располагает двумя газовыми насосами. В очереди, ведущей к насосам, могут расположиться не более пяти автомашин, включая те, которые обслуживаются. Если уже нет места, прибывающие автомобили уезжают искать другую заправку. Распределение прибывающих автомобилей является пуассоновским с математическим ожиданием 20 автомобилей в час. Время обслуживания клиентов имеет экспоненциальное распределение с математическим ожиданием 6 минут.
На основе расчета функциональных характеристик СМО определить:
– процент автомобилей, которые будут искать другую заправку;
– процент времени, когда используется только один из насосов;
– процент времени использования двух насосов;
– вероятность того, что прибывающий автомобиль найдет свободное место в очереди;
– среднее время пребывания автомобиля на газозаправочной станции.
массовый обслуживание транспорт автомобильный
Функциональные характеристики СМО
|
Характеристика |
Описание |
Значение |
| l | интенсивность входного потока заявок | 20 |
| m | интенсивность обслуживания | 10 |
| | относительная нагрузка на систему | 2,00000 |
|
эфф |
эффективная интенсивность поступления заявок в систему | 13,3333 |
|
Lq |
среднее число заявок в очереди | 2,00000 |
|
Ls |
среднее число находящихся в системе заявок | 3,73333 |
|
Wq |
средняя продолжительность пребывания заявки в очереди | 0,11538 |
|
Ws |
средняя продолжительность пребывания заявки в системе | 0,21538 |
|
p0 |
вероятность состояния S0 |
0,06667 |
|
p1 |
вероятность состояния S1 |
0,13333 |
|
P2 |
вероятность состояния S2 |
0,13333 |
|
P3 |
вероятность состояния S3 |
0,13333 |
|
P4 |
вероятность состояния S4 |
0,13333 |
|
P5 |
вероятность состояния S5 |
0,13333 |
|
P6 |
вероятность состояния S6 |
0,13333 |
|
P7 |
вероятность состояния S7 |
0,13333 |
Интерпретация полученных результатов.
– процент автомобилей, которые будут искать другую заправку = pc+m = p7 = 13,33%
– процент времени, когда используется только один из насосов = p1 = 13,33%
– процент времени использования двух насосов = p2 + … +p7 = 80%
– вероятность того, что прибывающий автомобиль найдет свободное место в очереди = 1 – p7 = 86,67%
– среднее время пребывания автомобиля на газозаправочной станции = Ws = 0,21538 ч. = 13 минут
Контрольные вопросы:
1. Из каких основных компонентов состоит СМО?
Системы массового обслуживания (СМО) – это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, которые удовлетворяются с помощью имеющихся в распоряжении системы каналов обслуживания (сервисов).
Основными компонентами СМО являются два потока событий:
1) входной поток заявок (требований на обслуживание), характеризующийся своей интенсивностью l (средним количеством клиентов, поступающих в систему в единицу времени) или средним интервалом времени между их последовательными поступлениями tпост;
2) выходной поток заявок, описываемый интенсивностью обслуживания m (средним количеством обслуженных заявок в единицу времени) или средней продолжительностью обслуживания tобсл.
Для СМО разомкнутого типа, у которых входной и выходной потоки подчинены распределению Пуассона, в качестве исходных данных для расчета функциональных характеристик используются:
· интенсивность входного потока заявок l;
· интенсивность обслуживания m;
· количеством параллельно работающих однородных сервисов (обслуживающих каналов) с;
· максимальная емкость очереди m;
· мощность источника заявок f.
2. Какие бывают СМО?
Состоянием системы называется число находящихся в данный момент в СМО заявок n. Поступающие заявки могут сразу попасть на обслуживание (если сервис свободен) или ожидать в очереди.
Если максимально допустимое число мест в очереди m конечно, то в СМО могут происходить отказы в предоставлении сервиса (система с отказами). Отклоняются от обслуживания те заявки, в момент прихода которых все места в очереди случайно оказались занятыми или при m = 0 (система без очереди) все каналы обслуживания оказались занятыми. В СМО с неограниченной длиной очереди (m = ¥) пришедшая заявка при невозможности немедленного обслуживания ожидает обслуживания при любой длине очереди и продолжительности времени ожидания.
По способу отбора из очереди заявок для обслуживания различают следующие виды дисциплины очереди:
1) первым пришел – первым обслуживается (FCFS);
2) последним пришел – первым обслуживается (LCFS);
3) случайный отбор заявок (SIRO);
4) ограничено время пребывания заявки в очереди;
5) с приоритетами, при которой некоторые находящиеся в очереди заявки имеют право первоочередного обслуживания (например, срочные работы выполняются раньше обычных).
По числу каналов обслуживания c различают одноканальные и многоканальные СМО. Многоканальные СМО разделяют:
· по характеристикам каналов – на однородные и неоднородные СМО;
· по расположению каналов – на СМО с параллельным и последовательным расположением сервисов.
В некоторых СМО интенсивность входного потока может зависеть от числа заявок, уже находящихся в системе (СМО замкнутого типа). В такой системе конечность очереди является следствием ограниченности мощности источника, создающего заявки на обслуживание. В СМО с источником бесконечной мощности (СМО разомкнутого типа) интенсивность входного потока практически не зависит от состояния системы.
3. Как определить основные функциональные характеристики СМО?
Наиболее употребляемыми функциональными характеристиками стационарных СМО являются следующие:
· pотк – вероятность отказа в обслуживании (средняя доля заявок, получивших отказ в обслуживании):
– для СМО с отказами
![]() ;
;
– для СМО с неограниченной очередью
pотк = 0;
· q – относительная пропускная способность системы (средняя доля обслуженных заявок; вероятность обслуживания)
q = 1 – pотк;
· – относительная нагрузка на систему
r = l / m;
· эфф – эффективная интенсивность поступления заявок в систему (абсолютная пропускная способность системы; среднее число заявок, обслуживаемых системой в единицу времени)
· Lq – среднее число заявок в очереди (средняя длина очереди):
– для СМО без очереди
Lq = 0;
– для СМО с ограниченной очередью

– для СМО с неограниченной очередью
![]() ;
;
· Ls – среднее число находящихся в системе заявок
· Wq – среднее время (средняя продолжительность) пребывания заявки в очереди
· Ws – среднее время (средняя продолжительность) пребывания заявки в системе
·
![]() – среднее
количество занятых средств обслуживания
– среднее
количество занятых средств обслуживания
![]() ;
;
· pn – вероятность того, что в системе находится n заявок
– для СМО с отказами
![]() ;
; 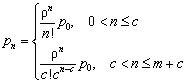 ;
;
– для СМО с неограниченной очередью
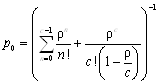 ;
;
В ходе работы я научилась определять количественные показатели качества функционирования системы массового обслуживания.
| Установки погружных центробежных насосов (УЭЦН) | |
|
СОДЕРЖАНИЕ лист Аннотация (русский язык) Аннотация (английский язык) ВВЕДЕНИЕ 1.АНАЛИЗ СУЩЕСТВУЮЩИХ СХЕМ И КОНСТРУКЦИЙ. 1.1.Назначение и технические ... Модули насосные устанавливаются между входным модулем и модулем-секцией погружного насоса. Комплектация несоотв. заявке |
Раздел: Рефераты по геологии Тип: реферат |
| ... для ремонта ходовой части легковых автомобилей для ГУ санаторий " ... | |
|
Федеральное агентство по образованию Владивостокский государственный университет экономики и сервиса Институт информатики инноваций и бизнес-систем ... Кафедра Сервиса и технической эксплуатации автомобилей Электрокарбюраторный цех предназначен для обслуживания приборов электрооборудования автомобиля, неисправность которых не может быть устранена при ТО непосредственно на автомобиле ... |
Раздел: Рефераты по транспорту Тип: дипломная работа |
| Разработка и исследование имитационной модели разветвленной СМО ... | |
|
Аннотация к работе "Разработка и исследование имитационной модели разветвленной СМО (системы массового обслуживания) в среде VB5" Работа посвящена ... В качестве таких показателей (в зависимости от обстановки и целей исследования) могут применяться разные величины, например: среднее число заявок, обслуживаемых СМО в единицу ... Это и есть формула Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время ... |
Раздел: Рефераты по радиоэлектронике Тип: реферат |
| ... обслуживания и ремонта карбюраторов двигателей легковых автомобилей | |
|
Введение Самый перспективный бизнес на рынке техники - автосервис. Спрос на автосервис постоянно увеличивается. Парк автомашин будет расти еще много ... Топливные фильтры для двигателей легковых автомобилей иногда выполняют совместно с карбюратором или топливным насосом. Показано, что для городских СТО производственная программа характеризуется числом комплексно обслуживаемых автомобилей в год, т.е. автомобилей, которым на станции выполняется весь ... |
Раздел: Рефераты по транспорту Тип: дипломная работа |
| Система массового обслуживания с ограниченным временем ожидания | |
|
Федеральное агентство по образованию РФ ФГОУ СПО "Перевозский строительный колледж" Курсовая работа по дисциплине "Математические методы" на тему "СМО ... Рассмотрим простейшую СМО с ожиданием - одноканальную систему (n - 1), в которую поступает поток заявок с интенсивностью ; интенсивность обслуживания (т.е. в среднем непрерывно ... Определим характеристики СМО: вероятность отказа , относительную пропускную способность q, абсолютную пропускную способность А, среднюю длину очереди , среднее число заявок ... |
Раздел: Рефераты по математике Тип: курсовая работа |