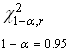Курсовая работа: Комплексная статистическая обработка экспериментальных данных
Министерство образования и науки Украины
Пояснительная записка
к курсовой работе
по дисциплине Статистика
Комплексная статистическая обработка экспериментальных данных
Реферат
Объектом исследования данной работы является комплексный анализ сгенерированных выборок случайных величин и подбор их закона распределения.
Целью работы является изучение методов и приемов анализа статистической информации, получение навыков и опыта работы в пакете STATISTICA.
В данной работе применялись широко используемые статистические методы обработки и анализа данных.
Результатом работы является освоение методов обработки данных статистического наблюдения, их анализа с помощью обобщающих показателей, установление теоретических законов распределения случайных величин и доказательство адекватности этих законов.
Данную курсовую работу можно использовать в качестве наглядного пособия по обработке статистических данных для различных учебных целей и задач.
Задание на курсовой проект
По специально сгенерированному имитатору получить последовательности случайных чисел двух типов:
а) ![]() ,
,
где ![]() – номер варианта,
– номер варианта,
![]() - номер измерения случайной величины,
- номер измерения случайной величины,
![]() – случайное число, возвращаемое при обращении к
стандартной функции выбранного языка программирования – датчику случайных
чисел.
– случайное число, возвращаемое при обращении к
стандартной функции выбранного языка программирования – датчику случайных
чисел.
б) ![]() .
.
Для исследований предусмотреть следующие объёмы измерений для каждой из случайных величин: 100, 200, …, 1000 (объёмы выборок).
Произвести статистический анализ каждой из полученных выборок для двух случайных величин в следующей последовательности:
а) найти размах варьирования;
б) определить целесообразное количество групп по формуле Стерджесса, построить группировку и интервальный ряд;
в) привести графическое изображение полигона частот, гистограммы, кумуляты и эмпирической функции распределения;
г) вычислить и
проанализировать точечные оценки ![]() и
и ![]() для простого и интервального рядов; построить и
проанализировать зависимость величины точечной оценки от объема выборки и от
номера эксперимента (10 выборок для объема выборки 1000);
для простого и интервального рядов; построить и
проанализировать зависимость величины точечной оценки от объема выборки и от
номера эксперимента (10 выборок для объема выборки 1000);
д) построить
доверительные интервалы для ![]() и
и ![]() , используя различные значения доверительной
вероятности (0,9; 0,95; 0,975; 0,995; 0,999) и проанализировать зависимость
длины доверительного интервала от объёма выборки и от величины доверительной
вероятности;
, используя различные значения доверительной
вероятности (0,9; 0,95; 0,975; 0,995; 0,999) и проанализировать зависимость
длины доверительного интервала от объёма выборки и от величины доверительной
вероятности;
е) вычислить и проанализировать медиану, коэффициент вариации, коэффициент асимметрии и эксцесс, моду; проанализировать зависимости числовых характеристик от объема выборки;
ж) оценить однородность каждой из выборок, используя:
1) коэффициент вариации;
2) метод ![]() -статистик Ирвина.
-статистик Ирвина.
з) определить, близки ли к нормальному распределению полученные эмпирические распределения на основе:
1) анализа числовых характеристик положения и вариации;
2) на основе критерия согласия Пирсона;
и) по виду гистограмм выдвинуть гипотезу о предполагаемых законах распределений исследуемых случайных величин, определить оценки параметров предполагаемых распределений (метод моментов и максимального правдоподобия) и проверить гипотезу о законе распределения по критерию Пирсона.
Введение
С давних пор человечество осуществляло учет многих сопутствующих его жизнедеятельности явлений и предметов, а также связанных с ними вычислений. Люди получали разносторонние, хотя и различающиеся полнотой сведения на различных этапах общественного развития. Данные учитывались повседневно в процессе принятия хозяйственных решений, а в обобщенном виде и на государственном уровне – при определении направления экономической и социальной политики, характера внешнеполитической деятельности.
Выполняя самые разнообразные функции сбора, систематизации и анализа сведений, характеризующих экономическое и социальное развитие общества, статистика всегда играла роль главного поставщика факторов для управленческих, научно-исследовательских и прикладных практических нужд различного рода структур, организаций и населения. Роль статистики в нашей жизни настолько значительна, что люди, часто не задумываясь и не осознавая, постоянно используют элементы статистической методологии в повседневной практике.
Применяя статистические методы в экономических исследованиях, можно осуществлять стратегическое планирование, а также анализировать и прогнозировать рыночную конъюнктуру, уменьшая степень неопределенности в отношении внешнего окружения.
С увеличением объемов информации, становится актуальным вопрос ее компьютерной обработки. Получение навыков обработки и анализа экспериментальных данных с помощью компьютера, например, в пакете STATISTICA дает возможность получить полную информацию об исследуемом объекте и найти оптимальное решение конкретной поставленной задачи.
1. Генерация исходных данных
В данной курсовой работе вместо статистического наблюдения используются случайные величины, сгенерированные по следующим формулам:
1) непрерывная случайная величина X, определяемая по формуле 1.1;
![]() (1.1)
(1.1)
2) непрерывная случайная величина У, определяемая по формуле 1.2.
![]() (1.2)
(1.2)
где ![]() ,
, ![]() - значения случайной величины X и У в различных опытах;
- значения случайной величины X и У в различных опытах;
![]() - случайное число, равномерно распределенное на
отрезке [0, 1], возвращаемое при обращении к стандартной функции на выбранном
языке программирования к датчику случайных чисел; Для генерации исходных
данных были использованы следующие методы:
- случайное число, равномерно распределенное на
отрезке [0, 1], возвращаемое при обращении к стандартной функции на выбранном
языке программирования к датчику случайных чисел; Для генерации исходных
данных были использованы следующие методы:
1) Для случайной величины ![]() в окне Variable в поле Long Name была введена формула 1.3:
в окне Variable в поле Long Name была введена формула 1.3:
![]() (1.3)
(1.3)
2) Для случайной величины ![]() был создан программный имитатор в модуле STATISTICA BASIC. Реализация алгоритма генерации данных в модуле STATISTICA BASIC приведена в приложении А.
был создан программный имитатор в модуле STATISTICA BASIC. Реализация алгоритма генерации данных в модуле STATISTICA BASIC приведена в приложении А.
В результате были получены выборки, объемом 100, 200…1000 значений для каждой из случайных величин.
2. Первичная обработка результатов наблюдения
2.1 Построение вариационного ряда
Вариационный ряд - упорядоченные по возрастанию значения признака.
Построение вариационного ряда в пакете STATISTICA производилось следующим образом:
в модуле Basic Statistics and Tables: Analysis → Frequency tables → кнопка Variables для выбора переменной → отметили All distinct values → ОК.
Размах варьирования ![]() – абсолютная величина разности между максимальным
– абсолютная величина разности между максимальным ![]() и минимальным
и минимальным ![]() значениями (вариантами) изучаемого признака:
значениями (вариантами) изучаемого признака:
![]() (2.1)
(2.1)
Построение размаха варьирования в пакете STATISTICA производилось следующим образом:
в модуле Basic Statistics and Tables: Analysis → Descriptive statistics → Variables (выбрать переменную) → нажали Box & whisker plot for all variables → выбрали Median / Quart. / Range → ОК.
Значения размаха варьирования для заданных выборок в таблице 2.1.
Таблица 2.1 – Размах варьирования для заданных выборок
|
|
|
|||||
| Выборка |
|
|
|
|
|
|
| 100 | 25,201 | 6,993 | 18,209 | 28,805 | 2,429 | 26,376 |
| 500 | 25,110 | 6,984 | 18,126 | 33,695 | 0,196 | 33,499 |
| 1000 | 25,237 | 6,711 | 18,466 | 33,962 | -1,574 | 35,536 |
Случайная величина ![]() имеет меньший размах, чем случайная величина
имеет меньший размах, чем случайная величина ![]() .
.
2.2 Группировка статистических данных
Число групп определяется по формуле Стерджесса (2.2):
![]() , (2.2)
, (2.2)
где ![]() – количество групп;
– количество групп;
![]() – объем выборки.
– объем выборки.
После определения числа групп следует определить интервалы группировки - значения варьирующего признака, лежащие в определенных границах. Величина равного интервала определяется по формуле (2.3):
|
где ![]() – число групп интервалов,
– число групп интервалов,
![]() – размах выборки .
– размах выборки .
Ниже приведены значения числа групп интервалов для всех выборок:
При ![]() :
: ![]() .
.
При ![]() :
: ![]() .
.
При ![]() :
:![]() .
.
При ![]() :
:![]() .
.
При ![]() :
: ![]() .
.
При ![]() :
:![]() .
.
При ![]() :
:![]() .
.
При ![]() :
:![]() .
.
При ![]() :
: ![]() .
.
При ![]() :
: ![]() .
.
Построение интервального ряда в пакете STATISTICA производилось следующим образом:
а) Analysis→Frequency tables→Variables(выбрали переменную);
б) установили количество интервалов в “No. of exact intervals”, посчитанных по формуле Стерджесса;
в) установили флажки в Display options:
- Cumulative frequencies – накопленные частоты;
- Percentages - частости;
- Cumulative percentages – накопленные частости.
Интервальные ряды по каждой выборке для случайных величин X и Y приведены в таблицах 2.2-2.7 и Д.1-Д.14.
Таблица 2.2 - Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. частота | Процент | Кумул. процент | |
| 5,475289<x<=8,510050 | 8 | 8 | 8,00000 | 8,0000 |
| 8,510050<x<=11,54481 | 15 | 23 | 15,00000 | 23,0000 |
| 11,54481<x<=14,57957 | 16 | 39 | 16,00000 | 39,0000 |
| 14,57957<x<=17,61433 | 18 | 57 | 18,00000 | 57,0000 |
| 17,61433<x<=20,64909 | 20 | 77 | 20,00000 | 77,0000 |
| 20,64909<x<=23,68385 | 13 | 90 | 13,00000 | 90,0000 |
| 23,68385<x<=26,71862 | 10 | 100 | 10,00000 | 100,0000 |
Таблица 2.3 -
Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. частота | Процент | Кумул. процент | |
| 5,850935<x<=8,116734 | 25 | 25 | 5,00000 | 5,0000 |
| 8,116734<x<=10,38253 | 62 | 87 | 12,40000 | 17,4000 |
| 10,38253<x<=12,64833 | 64 | 151 | 12,80000 | 30,2000 |
| 12,64833<x<=14,91413 | 55 | 206 | 11,00000 | 41,2000 |
| 14,91413<x<=17,17993 | 70 | 276 | 14,00000 | 55,2000 |
| 17,17993<x<=19,44573 | 64 | 340 | 12,80000 | 68,0000 |
| 19,44573<x<=21,71153 | 74 | 414 | 14,80000 | 82,8000 |
| 21,71153<x<=23,97733 | 59 | 473 | 11,80000 | 94,6000 |
| 23,97733<x<=26,24313 | 27 | 500 | 5,40000 | 100,0000 |
Таблица 2.4 -
Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. частота | Процент | Кумул. процент | |
| 5,745344<x<=7,797069 | 50 | 50 | 5,00000 | 5,0000 |
| 7,797069<x<=9,848795 | 106 | 156 | 10,60000 | 15,6000 |
| 9,848795<x<=11,90052 | 134 | 290 | 13,40000 | 29,0000 |
| 11,90052<x<=13,95225 | 88 | 378 | 8,80000 | 37,8000 |
| 13,95225<x<=16,00397 | 117 | 495 | 11,70000 | 49,5000 |
| 16,00397<x<=18,05570 | 121 | 616 | 12,10000 | 61,6000 |
| 18,05570<x<=20,10742 | 107 | 723 | 10,70000 | 72,3000 |
| 20,10742<x<=22,15915 | 117 | 840 | 11,70000 | 84,0000 |
| 22,15915<x<=24,21087 | 111 | 951 | 11,10000 | 95,1000 |
| 24,21087<x<=26,26260 | 49 | 1000 | 4,90000 | 100,0000 |
Таблица 2.5 -
Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 0,231076<x<=4,627075 | 1 | 1 | 1,00000 | 1,0000 |
| 4,627075<x<=9,023072 | 6 | 7 | 6,00000 | 7,0000 |
| 9,023072<x<=13,41907 | 20 | 27 | 20,00000 | 27,0000 |
| 13,41907<x<=17,81507 | 31 | 58 | 31,00000 | 58,0000 |
| 17,81507<x<=22,21107 | 22 | 80 | 22,00000 | 80,0000 |
| 22,21107<x<=26,60706 | 17 | 97 | 17,00000 | 97,0000 |
| 26,60706<x<=31,00306 | 3 | 100 | 3,00000 | 100,0000 |
Таблица 2.6 -
Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -1,89766<x<=2,289667 | 2 | 2 | 0,40000 | 0,4000 |
| 2,289667<x<=6,476997 | 21 | 23 | 4,20000 | 4,6000 |
| 6,476997<x<=10,66433 | 59 | 82 | 11,80000 | 16,4000 |
| 10,66433<x<=14,85166 | 125 | 207 | 25,00000 | 41,4000 |
| 14,85166<x<=19,03899 | 147 | 354 | 29,40000 | 70,8000 |
| 19,03899<x<=23,22632 | 99 | 453 | 19,80000 | 90,6000 |
| 23,22632<x<=27,41365 | 39 | 492 | 7,80000 | 98,4000 |
| 27,41365<x<=31,60098 | 7 | 499 | 1,40000 | 99,8000 |
Таблица 2.7 -
Интервальный ряд СВ ![]() при
при ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -3,54794<x<=0,400491 | 5 | 5 | 0,50000 | 0,5000 |
| 0,400491<x<=4,348925 | 9 | 14 | 0,90000 | 1,4000 |
| 4,348925<x<=8,297359 | 61 | 75 | 6,10000 | 7,5000 |
| 8,297359<x<=12,24579 | 177 | 252 | 17,70000 | 25,2000 |
| 12,24579<x<=16,19423 | 279 | 531 | 27,90000 | 53,1000 |
| 16,19423<x<=20,14266 | 267 | 798 | 26,70000 | 79,8000 |
| 20,14266<x<=24,09110 | 154 | 952 | 15,40000 | 95,2000 |
| 24,09110<x<=28,03953 | 38 | 990 | 3,80000 | 99,0000 |
| 28,03953<x<=31,98797 | 8 | 998 | 0,80000 | 99,8000 |
| 31,98797<x<=35,93640 | 2 | 1000 | 0,20000 | 100,0000 |
2.3 Графическое изображение рядов распределения
Графическое изображение интервальных рядов включает построения полигона частот, гистограммы и кумуляты.
В пакете STATISTICA построение полигона происходит следующим образом:
а) Analysis → Frequency tables → Variables (выбрать переменную);
б) установить количество интервалов в “No. of exact intervals”;
в) Frequency tables → Count;
г) нажать правую кнопку мыши и из выпадающего списка выбрать “Custom Graphs”;
д) 2D Graphs → Graph Type → Line Plot. [1]
Построение кумуляты:
а)Analysis → Frequency tables → Variables (выбрать переменную);
б) установить количество интервалов в “No. of exact intervals”;
в) Frequency tables → Cumul. Count;
г) нажать правую кнопку мыши и выбрать “Custom Graphs”;
д) 2D Graphs → Graph Type →
Line Plot (Bar ![]() ).
).
Построение гистограммы происходит следующим образом:
а) Analysis → Frequency tables → Variables (выбрать переменную);
б) установить количество интервалов в “No. of exact intervals”;
в) Frequency tables → Percent;
г) нажать правую кнопку мыши и из выпадающего списка выбрать “Custom Graphs”;
д) 2D Graphs → Graph Type →
Bar ![]()
2.4 Точечные оценки средних показателей
Точечная оценка математического ожидания по вариационному ряду вычисляется по формуле (2.4):
|
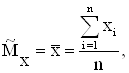
где ![]() – значения элементов выборки.
– значения элементов выборки.
Оценка дисперсии по вариационному ряду вычисляется по формуле (2.5).
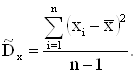
|
Вычисление оценки математического ожидания по интервальному вариационному ряду осуществляется по формуле (2.6):
|
где ![]() – середина
– середина ![]() -го интервала;
-го интервала;
![]() – статистическая вероятность
(частость) попадания в
– статистическая вероятность
(частость) попадания в ![]() -тый интервал.
-тый интервал.
Оценка дисперсии для интервального ряда вычисляется по формуле (2.7):
|
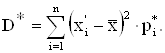
Вычисление точечных оценок по вариационному ряду в пакете STATISTICA:
Analysis → Descriptive statistics → Categorization → Number of intervals (установить количество интервалов) → More statistics → Mean, Variance. [2]
Значения точечных оценок математического ожидания и дисперсии для простого и интервального рядов приведены в таблице 2.8.
Таблица 2.8 – Оценки математического ожидания и дисперсии
| Выборка | Математическое ожидание | Дисперсия | ||
| Простой ряд | Интервальный ряд | Простой ряд | Интервальный ряд | |
|
|
16,254 | 16,279 | 27,849 | 28,517 |
|
|
16,189 | 16,174 | 26,259 | 26,598 |
|
|
15,950 | 16,006 | 27,608 | 28,330 |
|
|
16,668 | 16,936 | 31,125 | 31,113 |
|
|
15,989 | 16,007 | 30,406 | 31,242 |
|
|
15,792 | 15,740 | 27,059 | 28,636 |
Из приведенных данных видно, что полученные оценки математического ожидания и дисперсии по вариационному (простому) и интервальному рядам имеют близкие значения. Причем, чем больше объем выборки, тем более точный результат. От номера эксперимента, то есть от количества испытаний величины точечной оценки не зависят. Это видно на рисунках 2.25 – 2.32.
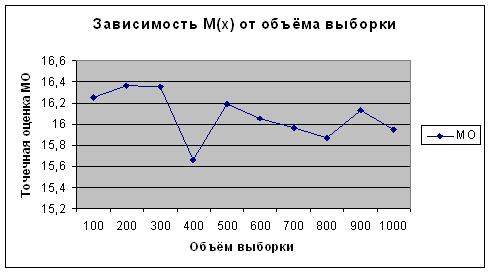
Рисунок 2.25 -
Зависимость ![]() от объема выборки для
от объема выборки для ![]()
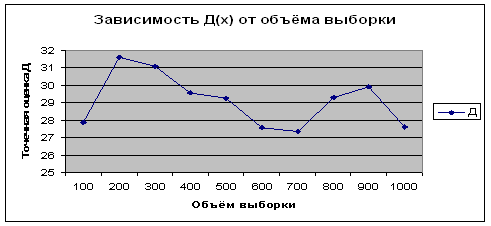
Рисунок 2.26 -
Зависимость ![]() от объема выборки для
от объема выборки для ![]()

Рисунок 2.27 -
Зависимость ![]() от объема выборки для
от объема выборки для ![]()
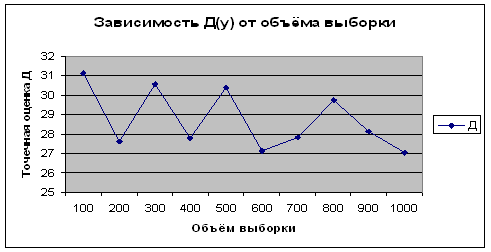
Рисунок 2.28 -
Зависимость ![]() от объема выборки для
от объема выборки для ![]()
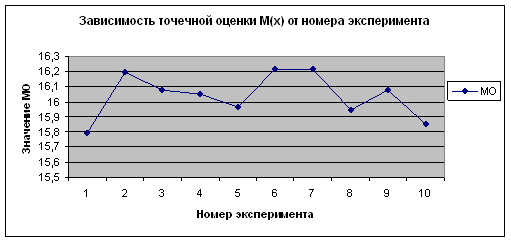
Рисунок 2.29 -
Зависимость ![]() от номера эксперимента по
от номера эксперимента по ![]()
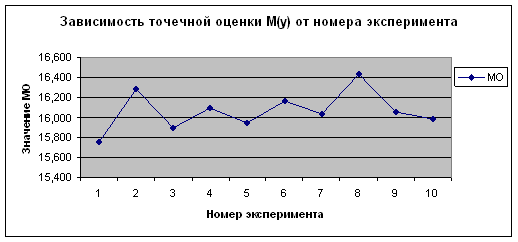
Рисунок 2.30 -
Зависимость ![]() от номера эксперимента по
от номера эксперимента по ![]()
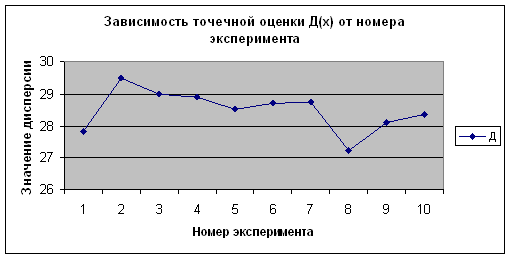
Рисунок 2.31 -
Зависимость ![]() от номера эксперимента по
от номера эксперимента по ![]()
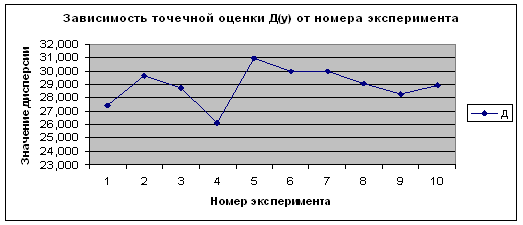
Рисунок 2.32 -
Зависимость ![]() от номера эксперимента по
от номера эксперимента по ![]()
В таблице 2.9 приведены
оценки математического ожидания и дисперсии, вычисленные для 10 выборок по 1000
элементов в каждой для случайной величины ![]() и случайной величины
и случайной величины ![]() .
.
Таблица 2.9 – Точечные
оценки выборок из 1000 элементов для ![]() и
и ![]()
|
|
|
|||
| Выборка |
|
|
|
|
| 1 | 15,792 | 27,832 | 15,754 | 27,421 |
| 2 | 16,193 | 29,501 | 16,283 | 29,650 |
| 3 | 16,076 | 29,006 | 15,900 | 28,716 |
| 4 | 16,052 | 28,884 | 16,096 | 26,124 |
| 5 | 15,968 | 28,508 | 15,947 | 30,983 |
| 6 | 16,212 | 28,710 | 16,163 | 29,956 |
| 7 | 16,215 | 28,747 | 16,030 | 30,011 |
| 8 | 15,945 | 27,243 | 16,428 | 29,069 |
| 9 | 16,080 | 28,103 | 16,054 | 28,265 |
| 10 | 15,853 | 28,369 | 15,980 | 28,913 |
2.5 Доверительные интервалы
Для того чтобы оценить достоверность оценок, вводят понятие доверительный интервал и доверительная вероятность.
|
![]()
где ![]() – математическое
ожидание генеральной совокупности;
– математическое
ожидание генеральной совокупности;
![]() - доверительная вероятность;
- доверительная вероятность;
![]() - оценка математического
ожидания;
- оценка математического
ожидания;
|
![]()
где ![]() - квантиль нормального
распределения, получается обратным интерполированием из таблицы для функции
распределения стандартного нормального закона. Вычисляется по формуле (2.9).
- квантиль нормального
распределения, получается обратным интерполированием из таблицы для функции
распределения стандартного нормального закона. Вычисляется по формуле (2.9).
|
|
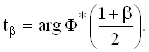
![]() - оценка дисперсии, вычисляется
по формуле (2.10).
- оценка дисперсии, вычисляется
по формуле (2.10).
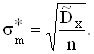
Доверительный интервал для дисперсии определяется по формуле (2.11).
|
![]()
где ![]() – дисперсия генеральной
совокупности;
– дисперсия генеральной
совокупности;
![]() – оценка дисперсии.
– оценка дисперсии.
![]() – квантиль нормального
распределения.
– квантиль нормального
распределения.
Оценка стандартного отклонения в зависимости от закона распределения случайной величины имеет различное значение.
Для нормального закона распределения эта величина будет равна:
![]()
Для равномерного:
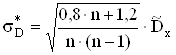
Ниже в таблицах 2.10-2.21 приведены доверительные интервалы математического ожидания исследуемых выборок.
-точный метод
Таблица 2.10 -
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
15,378 | 17,130 |
|
|
15,207 | 17,301 |
|
|
15,053 | 17,455 |
|
|
14,739 | 17,769 |
|
|
14,481 | 18,027 |
-грубый метод
Таблица 2.11 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
15,376 | 17,132 |
|
|
15,207 | 17,301 |
|
|
15,058 | 17,450 |
|
|
14,753 | 17,755 |
|
|
14,508 | 18,000 |
-точный метод
Таблица 2.12 -
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
15,811 | 16,566 |
|
|
15,738 | 16,639 |
|
|
15,673 | 16,704 |
|
|
15,542 | 16,835 |
|
|
15,408 | 16,940 |
-грубый метод
Таблица 2.13 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
15,795 | 16,553 |
|
|
15,722 | 16,626 |
|
|
15,657 | 16,691 |
|
|
15,526 | 16,822 |
|
|
15,420 | 16,928 |
-точный метод
Таблица 2.14 -
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
15,677 | 16,224 |
|
|
15,624 | 16,276 |
|
|
15,577 | 16,323 |
|
|
15,483 | 16,418 |
|
|
15,447 | 16,565 |
-грубый метод
Таблица 2.15 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
15,729 | 16,283 |
|
|
15,676 | 16,336 |
|
|
15,629 | 16,383 |
|
|
15,533 | 16,479 |
|
|
15,456 | 16,556 |
-точный метод
Таблица 2.16 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
15,742 | 17,595 |
|
|
15,561 | 17,775 |
|
|
15,399 | 17,938 |
|
|
15,066 | 18,270 |
|
|
15,084 | 18,788 |
-грубый метод
Таблица 2.17 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
16,018 | 17,854 |
|
|
15,843 | 18,029 |
|
|
15,687 | 18,185 |
|
|
15,369 | 18,503 |
|
|
15,112 | 18,760 |
-точный метод
Таблица 2.18 – Доверительные
интервалы для СВ ![]() ,
, ![]()
|
|
15,583 | 16,396 |
|
|
15,505 | 16,474 |
|
|
15,435 | 16,544 |
|
|
15,294 | 16,685 |
|
|
15,177 | 16,837 |
-грубый метод
Таблица 2.19 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
15,596 | 16,418 |
|
|
15,517 | 16,497 |
|
|
15,447 | 16,567 |
|
|
15,305 | 16,709 |
|
|
15,190 | 16,824 |
-точный метод
Таблица 2.20 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
15,521 | 16,063 |
|
|
15,469 | 16,115 |
|
|
15,423 | 16,161 |
|
|
15,329 | 16,255 |
|
|
15,178 | 16,302 |
-грубый метод
Таблица 2.21 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
15,462 | 16,018 |
|
|
15,408 | 16,072 |
|
|
15,361 | 16,119 |
|
|
15,264 | 16,216 |
|
|
15,187 | 16,293 |
Длины доверительных интервалов для математического ожидания при различных уровнях доверительной вероятности приведены в таблице 2.22.
Таблица 2.22 – Длины доверительных интервалов
| Длина интервала | |||||
|
|
|
|
|
|
|
|
|
1,752 | 2,094 | 2,402 | 3,03 | 3,546 |
|
|
0,755 | 0,901 | 1,031 | 1,293 | 1,532 |
|
|
0,547 | 0,652 | 0,746 | 0,935 | 1,118 |
|
|
1,853 | 2,214 | 2,539 | 3,204 | 3,704 |
|
|
0,813 | 0,969 | 1,109 | 1,391 | 1,66 |
|
|
0,542 | 0,646 | 0,738 | 0,926 | 1,124 |
В таблицах 2.23 – 2.34 указаны доверительные интервалы дисперсии исследуемых выборок.
-точный метод
Таблица 2.23 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
25,059 | 32,793 |
|
|
24,452 | 33,693 |
|
|
23,926 | 34,524 |
|
|
22,914 | 36,280 |
|
|
22,095 | 37,873 |
-грубый метод
Таблица 2.24 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
26,084 | 30,950 |
|
|
25,619 | 31,415 |
|
|
25,205 | 31,829 |
|
|
24,362 | 32,672 |
|
|
23,681 | 33,353 |
-точный метод
Таблица 2.25 – Доверительные
интервалы для СВ ![]() ,
, ![]()
|
|
23,373 | 30,586 |
|
|
22,807 | 31,426 |
|
|
22,316 | 32,201 |
|
|
21,372 | 33,838 |
|
|
20,608 | 35,324 |
-грубый метод
Таблица 2.26 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
24,329 | 28,867 |
|
|
23,895 | 29,301 |
|
|
23,508 | 29,688 |
|
|
22,722 | 30,474 |
|
|
22,088 | 31,108 |
-точный метод
Таблица 2.27 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
22,258 | 29,128 |
|
|
21,719 | 29,928 |
|
|
21,252 | 30,666 |
|
|
20,354 | 32,225 |
|
|
19,626 | 33,640 |
-грубый метод
Таблица 2.28 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
23,169 | 27,491 |
|
|
22,756 | 27,904 |
|
|
22,388 | 28,272 |
|
|
21,639 | 29,021 |
|
|
21,035 | 29,625 |
-точный метод
Таблица 2.29 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
27,340 | 35,779 |
|
|
26,678 | 36,761 |
|
|
26,104 | 37,667 |
|
|
25,000 | 39,582 |
|
|
24,106 | 41,321 |
-грубый метод
Таблица 2.30 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
28,459 | 33,767 |
|
|
27,951 | 34,275 |
|
|
27,499 | 34,727 |
|
|
26,579 | 35,647 |
|
|
25,837 | 36,389 |
-точный метод
Таблица 2.31 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
26,575 | 34,777 |
|
|
25,931 | 35,732 |
|
|
25,374 | 36,613 |
|
|
24,301 | 38,474 |
|
|
23,431 | 40,164 |
-грубый метод
Таблица 2.32 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
27,662 | 32,822 |
|
|
27,168 | 33,316 |
|
|
26,729 | 33,755 |
|
|
25,835 | 34,649 |
|
|
25,114 | 35,370 |
-точный метод
Таблица 2.33 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
25,163 | 32,930 |
|
|
24,554 | 33,834 |
|
|
24,026 | 34,668 |
|
|
23,010 | 36,431 |
|
|
22,187 | 38,031 |
-грубый метод
Таблица 2.34 –
Доверительные интервалы для СВ ![]() ,
, ![]()
|
|
26,193 | 31,079 |
|
|
25,726 | 31,546 |
|
|
25,310 | 31,962 |
|
|
24,463 | 32,809 |
|
|
23,780 | 33,492 |
В таблице 2.35 показано изменение длины доверительного интервала для дисперсии в зависимости от объема выборки и величины доверительной вероятности.
Таблица 2.35 – Длины доверительных интервалов
| Величина интервала | |||||
|
|
|
|
|
|
|
|
|
7,734 | 9,241 | 10,598 | 13,366 | 15,778 |
|
|
7,213 | 8,619 | 9,885 | 12,466 | 14,716 |
|
|
4,322 | 5,148 | 5,884 | 7,382 | 8,590 |
|
|
8,439 | 10,083 | 11,563 | 14,582 | 17,215 |
|
|
8,202 | 9,801 | 11,239 | 14,173 | 16,733 |
|
|
7,767 | 9,280 | 10,642 | 13,421 | 15,844 |
Анализируя полученные данные можно заметить, что при увеличении уровня доверительной вероятности увеличивается величина доверительного интервала, а при увеличении объема выборки она уменьшается. Это справедливо как для доверительных интервалов математического ожидания, так и для дисперсии. [3]
2.6 Другие точечные оценки интервального ряда (мода, медиана, коэффициент вариации, коэффициент асимметрии, эксцесс)
Модой в вариационном ряду является наиболее часто встречающееся значение признака.
Мода по интервальному ряду вычисляется по формуле (2.13):
![]() (2.13)
(2.13)
где ![]() – левая граница модального интервала (модальным
называется интервал, имеющий наибольшую частость);
– левая граница модального интервала (модальным
называется интервал, имеющий наибольшую частость);
![]() – величина интервала группировки;
– величина интервала группировки;
![]() – частота модального интервала;
– частота модального интервала;
![]() – частота интервала,
предшествующего модальному;
– частота интервала,
предшествующего модальному;
![]() – частота интервала, следующего
за модальным.
– частота интервала, следующего
за модальным.
Медиана – серединное наблюдение в выборке длиной n.
При нечетном n медиана в вариационном ряду есть
значение ряда с номером ![]() .
.
При четном n медиана есть полусумма значений с
номерами ![]() и
и
![]() . В
интервальном ряду для нахождения медианы применяется формула (2.14):
. В
интервальном ряду для нахождения медианы применяется формула (2.14):
|
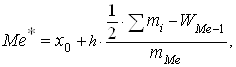
где ![]() – нижняя граница медианного интервала (медианным
называется интервал, накопленная частота которого превышает половину общей
суммы частот);
– нижняя граница медианного интервала (медианным
называется интервал, накопленная частота которого превышает половину общей
суммы частот);
![]() – величина интервала группировки;
– величина интервала группировки;
![]() – частота медианного интервала;
– частота медианного интервала;
![]() – накопленная частота интервала, предшествующего
медианному.
– накопленная частота интервала, предшествующего
медианному.
Коэффициент вариации вычисляется по формуле (2.15):
|
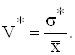
На основе момента третьего порядка (смотри формулу 2.16) выборочный коэффициент асимметрии находится по формуле (2.17):
|
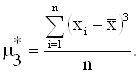
|
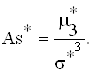
С помощью момента четвертого порядка характеризуют свойство рядов распределения, называемое эксцессом. Показатель эксцесса для ранжированного ряда находится по формуле (2.18).
|
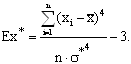
Вычисление точечных оценок по вариационному ряду в пакете STATISTICA происходит следующим образом:
Analysis → Descriptive statistics:
а) Categorization → Number of intervals (установить количество интервалов);
б) нажать кнопку More statistics → откроется окно Statistics, где можно выбрать следующие показатели:
- Mean – выборочное среднее;
- Median – медиана;
- Standard Deviation – стандартное отклонение среднего значения;
- Variance – выборочная дисперсия;
- Skewness – выборочный коэффициент асимметрии;
- Kurtosis – выборочный коэффициент эксцесса;
в) выбрать необходимые параметры и нажать ОК.
Значения медианы, коэффициента вариации, коэффициента ассиметрии и эксцесса приведены в таблице 2.36.
Таблица 2.36 - Медиана, коэффициент вариации, коэффициент ассиметрии и эксцесс
| Выборка | Медиана | Коэф. ассиметрии | Эксцесс | Коэф. вариации |
|
|
16,587 | -0,009 | -1,017 | 0,326 |
|
|
16,501 | -0,058 | -1,160 | 0,317 |
|
|
16,119 | 0,007 | -1,192 | 0,329 |
|
|
16,531 | -0,086 | -0,449 | 0,335 |
|
|
16,013 | -0,022 | -0,138 | 0,345 |
|
|
15,795 | -0,080 | 0,170 | 0,329 |
Анализируя полученные данные, можно сказать, что обе случайные величины имеют практически симметричное распределение, т. к. коэффициенты асимметрии всех выборок близки к нулю,
Случайная величина ![]() имеет более пологое распределение (эксцесс для всех
ее выборок имеет отрицательное значение). А эксцесс выборок случайной величины
имеет более пологое распределение (эксцесс для всех
ее выборок имеет отрицательное значение). А эксцесс выборок случайной величины ![]() практически равен нулю, т.е. "крутизна"
распределения случайной величины Y
близка к нормальному распределению.
практически равен нулю, т.е. "крутизна"
распределения случайной величины Y
близка к нормальному распределению.
2.7 Оценка однородности выборки
Любая исследуемая совокупность содержит как значения признаков, сложившихся под влиянием факторов, непосредственно характерных для анализируемой совокупности, так и значения признаков, полученных под воздействием иных факторов, не характерных для основной совокупности.
Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). [4]
Из таблицы 2.36 видно, что однородными можно считать выборки
случайной величины ![]() при
при ![]() равном 100, 500, 1000 и
равном 100, 500, 1000 и ![]() при n равном 1000.
при n равном 1000.
Однородность выборки
можно проверить, также используя метод Ирвина, основанный на определении ![]() -статистики. При его использовании выявление
аномальных наблюдений производится по формуле (2.19).
-статистики. При его использовании выявление
аномальных наблюдений производится по формуле (2.19).
|
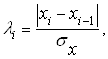
где ![]() – упорядоченная (по возрастанию или по убыванию)
исследуемая совокупность;
– упорядоченная (по возрастанию или по убыванию)
исследуемая совокупность;
![]() – значение ряда;
– значение ряда;
![]() – предыдущее значение ряда;
– предыдущее значение ряда;
![]() – среднеквадратическое отклонение.
– среднеквадратическое отклонение.
Если расчетное значение превысит уровень критического, то оно признается аномальным.
Произведя соответствующие
расчёты в Microsoft Excel мы убедились, что ни одно из расчётных значений не
превышает уровень критического значения. Это значит, что все выборки случайных
величин ![]() и
и ![]() – однородны.
– однородны.
2.8 Проверка нормальности эмпирического распределения
2.8.1 Проверка нормальности эмпирического распределения на основе анализа точечных оценок числовых характеристик
Если среднее арифметическое, медиана и мода имеют близкие значения, это указывает на вероятное соответствие изучаемого распределения нормальному закону. Для нормального распределения коэффициент асимметрии и эксцесса равны нулю, а для равномерного эксцесс равен -1,2.
В таблице 2.37 приведены данные для проверки вышеуказанных утверждений.
Таблица 2.37 – Анализ числовых характеристик положения и вариации
|
равномерный закон (СВ |
нормальный закон (СВ |
|||||||
| выборка |
|
|
|
выборка |
|
|
||
| 100 | 16,254 | 16,587 | -0,009 | -1,017 | 100 | 16,668 | 16,531 | -0,449 |
| 200 | 16,369 | 15,840 | 0,034 | -1,264 | 200 | 15,688 | 15,703 | 0,712 |
| 300 | 16,355 | 16,335 | -0,092 | -1,270 | 300 | 15,696 | 15,655 | 0,472 |
| 400 | 15,658 | 15,581 | 0,056 | -1,254 | 400 | 16,770 | 16,954 | -0,196 |
| 500 | 16,189 | 16,501 | -0,058 | -1,160 | 500 | 15,989 | 16,013 | -0,138 |
| 600 | 16,048 | 15,897 | -0,022 | -1,158 | 600 | 16,049 | 16,008 | -0,077 |
| 700 | 15,964 | 15,956 | -0,017 | -1,159 | 700 | 16,319 | 16,576 | -0,128 |
| 800 | 15,867 | 15,649 | 0,072 | -1,218 | 800 | 15,990 | 16,082 | 0,172 |
| 900 | 16,132 | 16,028 | -0,022 | -1,243 | 900 | 15,885 | 15,749 | -0,092 |
| 1000 | 15,950 | 16,119 | 0,007 | -1,192 | 1000 | 15,792 | 15,795 | 0,170 |
Анализируя полученные
данные, можно сделать вывод о том что значения медианы и среднего
арифметического для выборок случайной величины ![]() и
и ![]() имеют практически равное значение.
Для выборки
имеют практически равное значение.
Для выборки ![]() значение коэффициента ассиметрии, а
для выборки случайной величины
значение коэффициента ассиметрии, а
для выборки случайной величины ![]() значение эксцесса практически равно
0. Для случайной величины
значение эксцесса практически равно
0. Для случайной величины ![]() значение эксцесса практически -1,2.
Таким образом, все это свидетельствует о близости распределения случайной
величины
значение эксцесса практически -1,2.
Таким образом, все это свидетельствует о близости распределения случайной
величины ![]() нормальному распределению, а
случайной величины
нормальному распределению, а
случайной величины ![]() равномерному.
равномерному.
2.9 Определение закона распределения случайных величин
2.9.1 Определение закона распределения случайной величины по виду гистограммы
По виду гистограмм, приведенных на рисунках 2.19-2.21 делаем
предположение о том, что случайная величина ![]() подчиняется равномерному закону распределения, а
случайная величина
подчиняется равномерному закону распределения, а
случайная величина ![]() соответствует нормальному закону
распределения, что можно увидеть на рисунках 2.22-2.24.
соответствует нормальному закону
распределения, что можно увидеть на рисунках 2.22-2.24.
2.9.2 Определение оценок параметров распределений
Метод моментов
Метод моментов заключается в том, что определенное количество статистических начальных и (или) центральных моментов приравнивается к соответствующим теоретическим моментам распределения случайной величины. Уравнения метода показано в формуле (2.23).
|
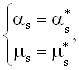
|
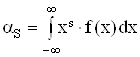 .
.
![]() – статистическая оценка
соответствующего теоретического момента
– статистическая оценка
соответствующего теоретического момента ![]() -того порядка, вычисляется по формуле (2.25):
-того порядка, вычисляется по формуле (2.25):
|
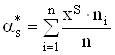 .
.
![]() – теоретический центральный момент s-того порядка, вычисляется по формуле
(2.26):
– теоретический центральный момент s-того порядка, вычисляется по формуле
(2.26):
|
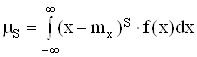 .
.
![]() – статистическая оценка
теоретического центрального момента
– статистическая оценка
теоретического центрального момента ![]() -того порядка, вычисляется по формуле (2.27):
-того порядка, вычисляется по формуле (2.27):
|
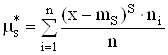 .
.
Из системы (2.23) находятся параметры распределения. Число уравнений в системе зависит от количества неизвестных параметров. Для нормального и равномерного законов, система должна содержать два уравнения, для экспоненциального – одно.
Для равномерного закона распределения система (2.23) принимает вид (2.28):
![]()
|
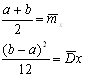
Из системы 2.28 нужно
найти параметры ![]() и
и ![]() .
.
В таблице 2.38 приведены значения этих параметров, найденные методом моментов и методом максимального правдоподобия.
Таблица 2.38 – Значения
параметров ![]() и
и ![]()
|
моментов) |
правдоподобия) |
∆ |
моментов) |
правдоподобия) |
∆ |
|
|
|
6,993 | 6,996 | 0,003 | 25,201 | 25,542 | 0,341 |
|
|
6,984 | 7,313 | 0,329 | 25,110 | 25,065 | 0,045 |
|
|
6,711 | 6,849 | 0,138 | 25,237 | 25,051 | 0,186 |
Из таблицы видно, что
значения параметров, найденные разными методами, практически совпадают. Это
подтверждает, что случайная величина ![]() распределена по равномерному закону.
распределена по равномерному закону.
Метод максимального правдоподобия
По методу максимального правдоподобия, строится так называемая функция правдоподобия (2.29):
|
где ![]() – выборка,
– выборка,
![]() – вектор параметров.
– вектор параметров.
Необходимо найти такие
значения вектора ![]() , чтобы функция
, чтобы функция ![]() достигала максимума. Для этого строят систему
правдоподобия (2.30), содержащую частные производные от функции правдоподобия
по всем переменным, приравненные к нулю. Для упрощения вычислений переходят к
функции
достигала максимума. Для этого строят систему
правдоподобия (2.30), содержащую частные производные от функции правдоподобия
по всем переменным, приравненные к нулю. Для упрощения вычислений переходят к
функции ![]() , равной логарифму натуральному от
, равной логарифму натуральному от ![]() :
:
|
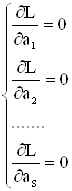 .
.
Оценки параметров, получаемые из этой системы, называют оценками максимального правдоподобия.
Для равномерного закона функция правдоподобия будет иметь вид (2.31)
|

где ![]() и
и ![]() – параметры распределения.
– параметры распределения.
Данная функция будет достигать максимума при условии (2.32):
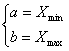
Судя по полученным
оценкам параметров распределения, можно сделать вывод, что наше предположение
было верно изначально и случайная величина ![]() действительно распределена равномерно.
действительно распределена равномерно.
2.10 Проверка нормальности эмпирического распределения на основе критериев согласия Пирсона
Для проверки гипотезы о соответствии эмпирического распределения нормальному закону распределения необходимо ввести нулевую гипотезу, которая будет проверяться по критерию Пирсона.
![]() : генеральная совокупность распределена по нормальному
закону.
: генеральная совокупность распределена по нормальному
закону.
В качестве меры
расхождения для критерия ![]() выбирается величина, равная
взвешенной сумме квадратов отклонений статистической вероятности от
соответствующей теоретической вероятности, рассчитанных по нормальному закону
теоретического распределения
выбирается величина, равная
взвешенной сумме квадратов отклонений статистической вероятности от
соответствующей теоретической вероятности, рассчитанных по нормальному закону
теоретического распределения ![]() вычисляется по формуле (2.20)
вычисляется по формуле (2.20)
|
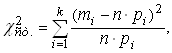
где ![]() – частота попадания в
i-тый интервал;
– частота попадания в
i-тый интервал;
![]() – объем выборки;
– объем выборки;
![]() – теоретическая вероятность попадания i-тый интервал:
– теоретическая вероятность попадания i-тый интервал:
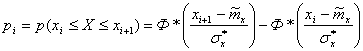
|
Общая схема применения
критерия ![]() :
:
1. Определение меры расхождения по формуле 2.20;
2.
Задание уровня
значимости ![]() ;
;
3.
Определение числа
степеней свободы ![]() по формуле 2.22.
по формуле 2.22.
![]() , (2.22)
, (2.22)
где ![]() – количество интервалов в интервальном ряду;
– количество интервалов в интервальном ряду;
![]() – число налагаемых связей, равное числу параметров
– число налагаемых связей, равное числу параметров
предполагаемого закона распределения
4. Область принятия основной гипотезы:
![]() .
.
Выполнение в пакете STATISTICA.
В модуле Nonparametric Statistics (непараметрическая статистика), Distribution Fitting. В поле Continuous Distributions представлены непрерывные распределения, а в поле Discrete Distributions - дискретные распределения (закон распределения выбираем дважды щелкнув на его название мышью) ® Variable (выбрать переменную) ® в поле Plot distribution выбираем Frequency distribution (частоты распределения) ® в поле Kolmogorov-Smirnov test ставим No → установим необходимые параметры числа интервалов, верхней и нижней границ, среднего и дисперсии → Graph. Результаты проверки соответствия гипотезы приведены в таблице 2.39 и показаны на рисунках 2.41-2.46
Таблица 2.39 – Значения ![]() и χ2крит для случайных
величин
и χ2крит для случайных
величин ![]() и
и
![]()
| Выборка |
|
|
|
Гипотеза |
|
|
4 | 9,49 | 7,53 | Принимается |
|
|
4 | 9,49 | 11,815 | Отвергается |
|
|
5 | 11,1 | 11,95 | Отвергается |
|
|
5 | 11,1 | 25,54 | Отвергается |
|
|
6 | 12,59 | 45,51 | Отвергается |
|
|
6 | 12,59 | 39,83 | Отвергается |
|
|
6 | 12,59 | 48,77 | Отвергается |
|
|
7 | 14,1 | 40,81 | Отвергается |
|
|
7 | 14,1 | 49,97 | Отвергается |
|
|
7 | 14,1 | 76,75 | Отвергается |
|
|
4 | 9,49 | 2,04 | Принимается |
|
|
4 | 9,49 | 2,12 | Принимается |
|
|
5 | 11,1 | 2,78 | Принимается |
|
|
5 | 11,1 | 2,99 | Принимается. |
|
|
6 | 12,59 | 3,15 | Принимается |
|
|
6 | 12,59 | 4,61 | Принимается |
|
|
6 | 12,59 | 5,07 | Принимается |
|
|
7 | 14,1 | 5,86 | Принимается |
|
|
7 | 14,1 | 6,32 | Принимается |
|
|
7 | 14,1 | 7,16 | Принимается |
На основе полученных
данных можно сделать вывод, что случайная величина ![]() распределена по нормальному
закону, а случайная величина
распределена по нормальному
закону, а случайная величина ![]() не распределена по нормальному
закону.
не распределена по нормальному
закону.
Анализируя получившиеся
графики, делаем вывод, что случайная величина ![]() распределена по равномерному закону, а случайная величина
распределена по равномерному закону, а случайная величина
![]() – по нормальному.
– по нормальному.
Заключение
В ходе курсовой работы были освоены методы обработки данных статистического наблюдения, их анализа с помощью обобщающих показателей, установление теоретических законов распределения случайных величин и доказательство адекватности этих законов. Также в результате выполнения данной работы мы приобрели навыки и опыт работы в пакете STATISTICА.
В ходе анализа данных, были сделаны выводы, что основной частью статистического анализа является выявление закона распределения случайной величины, а также, выявление основных факторов, оказывающих влияние на качество оцениваемых параметров закона распределения (длина выборки, её однородность, величина доверительной вероятности). Был произведен статистический анализ каждой из полученных в ходе генерации выборок данных двух случайных величин, был найден закон их распределения. Рассмотрены основные числовые характеристики положения и вариации нормального и равномерного закона.
Полученный опыт работы со статистическими данными и методами их обработки на компьютере позволит гораздо быстрее и эффективнее применять эти методы обработки информации в повседневной жизни, в частности, для экономических исследований и разработок.
Перечень ссылок
случайный величина интервальный выборка
1. Теория статистики: Учебник / Под ред. проф. Р. А. Шмойловой. - 3-е изд., перераб. -М.: Финансы и статистика, 2000. - 560 с.
2. Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник / Под ред. чл.-корр. РАН И. И. Елисеевой. – М.: Финансы и статистика, 1998. – 365 с.: ил.
3. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. – М.: Наука, 1969. – 509 с.
4. Гурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для втузов. Изд. 5-е перераб. и доп. – М.: Высш. школа, 1977. – 397 с.
5. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: Unity, 2000. – 544 с.
6. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969. – 576 с.
7. Боровиков В. STATISTICA: искусство анализа данных на компьютере. Для профессионалов. - СПб.: Питер, 2001. - 656 с.
Приложение А
Генерация исходных данных
СВ ![]() в пакете STATISTICA
в пакете STATISTICA
Dim ADS As Spreadsheet
Dim STBReport As Report
Dim SUM As Double
Dim LOOP_CASE As Double
Dim I As Double
Sub Main
Set ADS = ActiveDataSet
Set STBReport = Reports.New
For LOOP_CASE = 1 To NCASES(ADS)
For I = 1 To n
SUM = 0
For L = 1 To 300
SUM = SUM + Uniform(1)
Next L
ADS.Value (LOOP_CASE, 1) = N * ((1 / 15) * SUM - 9)
Next I
NEXT_CASE:
Next LOOP_CASE
End Sub
Приложение Б
Интервальные ряды для СВ ![]() и
и ![]()
Таблица Д.1 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,289175<x<=8,355050 | 14,000 | 14,000 | 7,000 | 7,000 |
| 8,355050<x<=11,42093 | 34,000 | 48,000 | 17,000 | 24,000 |
| 11,42093<x<=14,48680 | 33,000 | 81,000 | 16,500 | 40,500 |
| 14,48680<x<=17,55268 | 33,000 | 114,000 | 16,500 | 57,000 |
| 17,55268<x<=20,61855 | 29,000 | 143,000 | 14,500 | 71,500 |
| 20,61855<x<=23,68443 | 23,000 | 166,000 | 11,500 | 83,000 |
| 23,68443<x<=26,75030 | 34,000 | 200,000 | 17,000 | 100,000 |
Таблица Д.2 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,502861<x<=8,114160 | 25,000 | 25,000 | 8,333 | 8,333 |
| 8,114160<x<=10,72546 | 37,000 | 62,000 | 12,333 | 20,667 |
| 10,72546<x<=13,33676 | 40,000 | 102,000 | 13,333 | 34,000 |
| 13,33676<x<=15,94806 | 39,000 | 141,000 | 13,000 | 47,000 |
| 15,94806<x<=18,55936 | 39,000 | 180,000 | 13,000 | 60,000 |
| 18,55936<x<=21,17066 | 41,000 | 221,000 | 13,667 | 73,667 |
| 21,17066<x<=23,78195 | 51,000 | 272,000 | 17,000 | 90,667 |
| 23,78195<x<=26,39325 | 28,000 | 300,000 | 9,333 | 100,000 |
Таблица Д.3 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,555859<x<=8,176674 | 33,000 | 33,000 | 8,250 | 8,250 |
| 8,176674<x<=10,79749 | 69,000 | 102,000 | 17,250 | 25,500 |
| 10,79749<x<=13,41830 | 54,000 | 156,000 | 13,500 | 39,000 |
| 13,41830<x<=16,03912 | 54,000 | 210,000 | 13,500 | 52,500 |
| 16,03912<x<=18,65993 | 51,000 | 261,000 | 12,750 | 65,250 |
| 18,65993<x<=21,28075 | 58,000 | 319,000 | 14,500 | 79,750 |
| 21,28075<x<=23,90156 | 54,000 | 373,000 | 13,500 | 93,250 |
| 23,90156<x<=26,52238 | 27,000 | 400,000 | 6,750 | 100,000 |
Таблица Д.4 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,616825<x<=7,918099 | 42,000 | 42,000 | 7,000 | 7,000 |
| 7,918099<x<=10,21937 | 60,000 | 102,000 | 10,000 | 17,000 |
| 10,21937<x<=12,52065 | 79,000 | 181,000 | 13,167 | 30,167 |
| 12,52065<x<=14,82192 | 78,000 | 259,000 | 13,000 | 43,167 |
| 14,82192<x<=17,12319 | 75,000 | 334,000 | 12,500 | 55,667 |
| 17,12319<x<=19,42447 | 69,000 | 403,000 | 11,500 | 67,167 |
| 19,42447<x<=21,72574 | 92,000 | 495,000 | 15,333 | 82,500 |
| 21,72574<x<=24,02701 | 70,000 | 565,000 | 11,667 | 94,167 |
| 24,02701<x<=26,32829 | 35,000 | 600,000 | 5,833 | 100,000 |
Таблица Д.5 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,638499<x<=7,943963 | 48,000 | 48,000 | 6,857 | 6,857 |
| 7,943963<x<=10,24943 | 80,000 | 128,000 | 11,429 | 18,286 |
| 10,24943<x<=12,55489 | 80,000 | 208,000 | 11,429 | 29,714 |
| 12,55489<x<=14,86035 | 100,000 | 308,000 | 14,286 | 44,000 |
| 14,86035<x<=17,16582 | 91,000 | 399,000 | 13,000 | 57,000 |
| 17,16582<x<=19,47128 | 83,000 | 482,000 | 11,857 | 68,857 |
| 19,47128<x<=21,77675 | 94,000 | 576,000 | 13,429 | 82,286 |
| 21,77675<x<=24,08221 | 89,000 | 665,000 | 12,714 | 95,000 |
| 24,08221<x<=26,38767 | 35,000 | 700,000 | 5,000 | 100,000 |
Таблица Д.6 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,746050<x<=7,794074 | 50,000 | 50,000 | 6,250 | 6,250 |
| 7,794074<x<=9,842099 | 87,000 | 137,000 | 10,875 | 17,125 |
| 9,842099<x<=11,89012 | 88,000 | 225,000 | 11,000 | 28,125 |
| 11,89012<x<=13,93815 | 110,000 | 335,000 | 13,750 | 41,875 |
| 13,93815<x<=15,98617 | 77,000 | 412,000 | 9,625 | 51,500 |
| 15,98617<x<=18,03420 | 84,000 | 496,000 | 10,500 | 62,000 |
| 18,03420<x<=20,08222 | 83,000 | 579,000 | 10,375 | 72,375 |
| 20,08222<x<=22,13025 | 77,000 | 656,000 | 9,625 | 82,000 |
| 22,13025<x<=24,17827 | 96,000 | 752,000 | 12,000 | 94,000 |
| 24,17827<x<=26,22630 | 48,000 | 800,000 | 6,000 | 100,000 |
Таблица Д.7 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 5,747041<x<=7,795948 | 46,000 | 46,000 | 5,111 | 5,111 |
| 7,795948<x<=9,844855 | 118,000 | 164,000 | 13,111 | 18,222 |
| 9,844855<x<=11,89376 | 93,000 | 257,000 | 10,333 | 28,556 |
| 11,89376<x<=13,94267 | 84,000 | 341,000 | 9,333 | 37,889 |
| 13,94267<x<=15,99158 | 107,000 | 448,000 | 11,889 | 49,778 |
| 15,99158<x<=18,04048 | 85,000 | 533,000 | 9,444 | 59,222 |
| 18,04048<x<=20,08939 | 108,000 | 641,000 | 12,000 | 71,222 |
| 20,08939<x<=22,13830 | 88,000 | 729,000 | 9,778 | 81,000 |
| 22,13830<x<=24,18720 | 108,000 | 837,000 | 12,000 | 93,000 |
| 24,18720<x<=26,23611 | 63,000 | 900,000 | 7,000 | 100,000 |
Таблица Д.8 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -3,85839<x<=1,661475 | 2,000 | 2,000 | 1,000 | 1,000 |
| 1,661475<x<=7,181336 | 7,000 | 9,000 | 3,500 | 4,500 |
| 7,181336<x<=12,70120 | 47,000 | 56,000 | 23,500 | 28,000 |
| 12,70120<x<=18,22106 | 79,000 | 135,000 | 39,500 | 67,500 |
| 18,22106<x<=23,74092 | 54,000 | 189,000 | 27,000 | 94,500 |
| 23,74092<x<=29,26078 | 8,000 | 197,000 | 4,000 | 98,500 |
| 29,26078<x<=34,78064 | 3,000 | 200,000 | 1,500 | 100,000 |
Таблица Д.9 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -3,50252<x<=1,766314 | 2,000 | 2,000 | 0,667 | 0,667 |
| 1,766314<x<=7,035144 | 13,000 | 15,000 | 4,333 | 5,000 |
| 7,035144<x<=12,30397 | 63,000 | 78,000 | 21,000 | 26,000 |
| 12,30397<x<=17,57280 | 106,000 | 184,000 | 35,333 | 61,333 |
| 17,57280<x<=22,84163 | 91,000 | 275,000 | 30,333 | 91,667 |
| 22,84163<x<=28,11046 | 21,000 | 296,000 | 7,000 | 98,667 |
| 28,11046<x<=33,37929 | 3,000 | 299,000 | 1,000 | 99,667 |
| 33,37929<x<=38,64812 | 1,000 | 300,000 | 0,333 | 100,000 |
Таблица Д.10 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| 1,299935<x<=5,325310 | 5,000 | 5,000 | 1,250 | 1,250 |
| 5,325310<x<=9,350685 | 31,000 | 36,000 | 7,750 | 9,000 |
| 9,350685<x<=13,37606 | 63,000 | 99,000 | 15,750 | 24,750 |
| 13,37606<x<=17,40143 | 117,000 | 216,000 | 29,250 | 54,000 |
| 17,40143<x<=21,42681 | 109,000 | 325,000 | 27,250 | 81,250 |
| 21,42681<x<=25,45218 | 55,000 | 380,000 | 13,750 | 95,000 |
| 25,45218<x<=29,47756 | 16,000 | 396,000 | 4,000 | 99,000 |
| 29,47756<x<=33,50293 | 4,000 | 400,000 | 1,000 | 100,000 |
Таблица Д.11 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -1,98797<x<=1,772650 | 1,000 | 1,000 | 0,167 | 0,167 |
| 1,772650<x<=5,533271 | 12,000 | 13,000 | 2,000 | 2,167 |
| 5,533271<x<=9,293892 | 54,000 | 67,000 | 9,000 | 11,167 |
| 9,293892<x<=13,05451 | 100,000 | 167,000 | 16,667 | 27,833 |
| 13,05451<x<=16,81513 | 166,000 | 333,000 | 27,667 | 55,500 |
| 16,81513<x<=20,57576 | 154,000 | 487,000 | 25,667 | 81,167 |
| 20,57576<x<=24,33638 | 88,000 | 575,000 | 14,667 | 95,833 |
| 24,33638<x<=28,09700 | 17,000 | 592,000 | 2,833 | 98,667 |
| 28,09700<x<=31,85762 | 8,000 | 600,000 | 1,333 | 100,000 |
Таблица Д.12 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -2,68355<x<=1,245110 | 2,000 | 2,000 | 0,286 | 0,286 |
| 1,245110<x<=5,173768 | 10,000 | 12,000 | 1,429 | 1,714 |
| 5,173768<x<=9,102425 | 41,000 | 53,000 | 5,857 | 7,571 |
| 9,102425<x<=13,03108 | 149,000 | 202,000 | 21,286 | 28,857 |
| 13,03108<x<=16,95974 | 180,000 | 382,000 | 25,714 | 54,571 |
| 16,95974<x<=20,88840 | 178,000 | 560,000 | 25,429 | 80,000 |
| 20,88840<x<=24,81705 | 102,000 | 662,000 | 14,571 | 94,571 |
| 24,81705<x<=28,74571 | 31,000 | 693,000 | 4,429 | 99,000 |
| 28,74571<x<=32,67437 | 7,000 | 700,000 | 1,000 | 100,000 |
Таблица Д.13 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -1,52038<x<=2,421483 | 4,000 | 4,000 | 0,500 | 0,500 |
| 2,421483<x<=6,363342 | 37,000 | 41,000 | 4,625 | 5,125 |
| 6,363342<x<=10,30520 | 69,000 | 110,000 | 8,625 | 13,750 |
| 10,30520<x<=14,24706 | 185,000 | 295,000 | 23,125 | 36,875 |
| 14,24706<x<=18,18892 | 231,000 | 526,000 | 28,875 | 65,750 |
| 18,18892<x<=22,13078 | 175,000 | 701,000 | 21,875 | 87,625 |
| 22,13078<x<=26,07264 | 75,000 | 776,000 | 9,375 | 97,000 |
| 26,07264<x<=30,01449 | 20,000 | 796,000 | 2,500 | 99,500 |
| 30,01449<x<=33,95635 | 3,000 | 799,000 | 0,375 | 99,875 |
| 33,95635<x<=37,89821 | 1,000 | 800,000 | 0,125 | 100,000 |
Таблица Д.14 - Интервальный ряд СВ ![]() ,
, ![]()
| Частота | Кумул. | Процент | Кумул. | |
| -1,06170<x<=2,578305 | 3,000 | 3,000 | 0,333 | 0,333 |
| 2,578305<x<=6,218309 | 36,000 | 39,000 | 4,000 | 4,333 |
| 6,218309<x<=9,858313 | 71,000 | 110,000 | 7,889 | 12,222 |
| 9,858313<x<=13,49832 | 171,000 | 281,000 | 19,000 | 31,222 |
| 13,49832<x<=17,13832 | 277,000 | 558,000 | 30,778 | 62,000 |
| 17,13832<x<=20,77832 | 176,000 | 734,000 | 19,556 | 81,556 |
| 20,77832<x<=24,41833 | 110,000 | 844,000 | 12,222 | 93,778 |
| 24,41833<x<=28,05833 | 47,000 | 891,000 | 5,222 | 99,000 |
| 28,05833<x<=31,69833 | 7,000 | 898,000 | 0,778 | 99,778 |
| 31,69833<x<=35,33834 | 2,000 | 900,000 | 0,222 | 100,000 |
| Серьёзные лекции по высшей экономической математике | |
|
Комбинаторные задачи. 1.Сколькими способами колода в 52 карты может быть роздана 13-ти игрокам так, чтобы каждый игрок получил по одной карте каждой ... Для доказательства несмещённости некоторых точечных оценок будем рассматривать выборку объема n как систему n независимых случайных величин x1, x2,... xn , каждая из которых имеет ... Пусть случайная величина (можно говорить о генеральной совокупности) распределена по нормальному закону, для которого известна дисперсия D = 2 ( > 0). Из генеральной совокупности ... |
Раздел: Рефераты по математике Тип: реферат |
|
4. МЕТОД ВЫБОРОЧНЫХ НАБЛЮДЕНИЙ 4.1. Выборочное исследование При статистическом исследовании экономических явлений могут применяться выборочные ... Основная масса элементов засоренной выборки является реализацией случайной величины X , закон распределения которой известен. Значение коэффициента доверия зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n . Английский ученый Стьюдент доказал, что в случаях ... |
Раздел: Рефераты по статистике Тип: реферат |
| Трансформации социально-экономических систем в КНР и Венгрии | |
|
Санкт-Петербургский государственный политехнический университет Институт интеллектуальных систем и технологий Кафедра Мировой экономики Курсовой ... изучение распределения частот значений переменной (изучение вариационных рядов) Предполагается, что случайная величина у имеет нормальный закон распределения с условным математическим ожиданием y, являющимся функцией от аргументов xj и постоянной, не зависящей ... |
Раздел: Рефераты по международным отношениям Тип: реферат |
|
Министерство образования Украины Харьковский государственный технический университет радиоэлектроники Кафедра ПОЭВМ Комплексная курсовая работа по ... Доверительный интервал для дисперсии (2,78993E+11; 5,36744E+11). Получим следующее количество интервалов группировки размах/длина интервала=9.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в табл. |
Раздел: Рефераты по экономико-математическому моделированию Тип: реферат |
| Организация и содержание элективного курса "Основы теории ... | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования "Вятский государственный ... Для интервального вариационного ряда ломаная начинается с точки, абсцисса, которой равна началу первого интервала, а ордината - накопленной частоте, равной нулю. 2. Дискретная случайная величина имеет только 2 возможных значения х и у, причем x<y. Вероятность того, что Х примет значение х =0,6. Найти закон распределения величины Х, если ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |