Курсовая работа: Психолого-педагогический анализ процесса развития мышления у детей шестого года жизни посредством игр
Содержание
Введение
Глава 1. Теоретические основы развития мышления у детей шестого года жизни посредством занимательных задач
Глава 2. Педагогические условия развития мышления у детей шестого года жизни посредством занимательных задач
2.1 Особенности развития мышления у детей шестого года жизни посредством занимательных задач
2.2 Педагогические условия развития мышления посредством игровых занимательных задач у детей шестого года жизни
Заключение
Библиография
Введение
«Научные понятия не усваиваются и не заучиваются ребенком, не берутся памятью, а возникают и складываются с помощью величайшего напряжения всей активности его собственной мысли». [8; 5]
Мышление отражает предметы и явления действительности в их существенных признаках, связях и отношениях. Оно опирается на данные чувственного познания, но выходит за его пределы, проникая в суть явлений, постигая те свойства и отношения, которые непосредственно в восприятии не даны.
Познавательная деятельность начинается с ощущений и восприятий. Умственное развитие человека необходимо совершается в процессе усвоения знаний, выработанных человечеством в ходе общественно-исторического развития.
В дошкольном возрасте ребенку приходится разрешать все более сложные и разнообразные задачи, требующие выделения и использования связей и отношений между предметами, явлениями, действиями. По мере развития любознательности, познавательных интересов мышление все шире используется детьми для познания окружающего мира, которое выходит за рамки задач, выдвигаемых их собственной практической деятельностью.
Формированию и развитию основных структур мышления способствуют игры, насыщенные логическим и математическим содержанием. Эти игры не требуют от детей каких–нибудь особых знаний. В них моделируются такие логические и математические конструкции, а в процессе игры решаются такие задачи, которые способствуют ускорению формирования и развития у дошкольников шестого года жизни простейших логических структур мышления и математических представлений.
Исследованием данной проблемы занимались такие отечественные психологи как: Выготский Л.С., Венгер Л.А., Мухина В.С., Леонтьев А.Н., Поддъяков Н.Н.
Поэтому целью нашего исследования является поиск эффективных педагогических условий, способствующих развитию мышления у детей шестого года жизни посредством игровых занимательных задач.
Объект исследования: процесс развития мышления у детей шестого года жизни посредством игровых занимательных задач.
Предмет исследования: педагогические условия, способствующие развитию мышления у детей шестого года жизни посредством игровых занимательных задач.
Гипотеза: развитие мышления у детей шестого года жизни посредством занимательных задач будет эффективным, если:
1. Использовать в работе с детьми шестого года жизни занимательные и доступные по возрасту игровые математические задачи.
2. Игровые занимательные задачи вводить в обучение детей постепенно, в порядке усложнения трудности их решения.
3. Учить детей приемам самостоятельного поиска решения задач, не предлагая готовых образцов.
4. Дети будут решать занимательные задачи не только на занятиях, но и вне занятий.
Задачи исследования:
1. Проанализировать психолого-педагогическую литературу по проблеме развития мышления детей шестого года жизни.
2. Выявить особенности развития мышления детей шестого года жизни посредством игровых занимательных задач.
3. Разработать эффективные педагогические условия, способствующие развитию мышления у детей шестого года жизни посредством игровых занимательных задач.
Методы исследования: анализ психолого-педагогической и методической литературы по проблеме; педагогический эксперимент; качественный и количественный анализ экспериментальных данных.
Глава 1. Теоретические основы развития мышления у детей шестого года жизни посредством занимательных задач
Мышление – одно из высших психических проявлений; процесс познавательной деятельности человека, характеризующийся обобщенным и опосредованным отражением действительности. Мышление как процесс неразрывно связано с мышлением как деятельностью личности. Термин охватывает различные виды деятельности (творчество, интеллектуальные упражнения, решение проблем). Считается, что в каждом случае человек пользуется мышлением. Виды мышления имеют следующие особенности:
· Мышление символично (в нем участвуют слова и образы).
· Процесс мышления не поддается наблюдению, но его существование выводится через логические умозаключения.
· В процессе мышления происходит манипуляция с неким смысловым содержанием. [6; 180]
Мышлением называется отражение связей и отношений между предметами и явлениями действительности, ведущее к получению новых знаний. [1; 169]
По определению Леонтьева А.Н.: « Мышление – процесс отражения объективной реальности, составляющий высшую степень человеческого познания».
Отличие мышления от других психических процессов состоит в том, что оно почти всегда связано с наличием проблемной ситуации, задачи, которую надо решить, и активным изменением условий, в которых эта задача задана.
Мышление в отличие от других процессов совершается в соответствии с определенной логикой.
На практике мышление как отдельный психический процесс не существует, оно незримо присутствует во всех других познавательных процессах: в восприятии, внимании, воображении, памяти, речи. Высшие формы этих процессов обязательно связаны с мышлением, и степень его участия в этих познавательных процессах определяет их уровень развития. [13; 182]
В чем же суть мышления? Во-первых: мышление есть опосредованное познание. К опосредованному познанию человек прибегает в следующих случаях:
1. когда непосредственное познание, невозможно из-за совершенства наших анализаторов;
2. когда непосредственное познание невозможно в силу временных, пространственных, технических ограничений, так как мышление радикально расширяет возможности человека в его стремлении к познанию всего окружающего мира, вплоть до невидимого и не представляемого, поскольку оно оперирует не только первичными и вторичными образами, но и понятиями.
3. когда непосредственное познание возможно, но не рационально.
Во-вторых: мышление есть познание отношений и закономерных связей между предметами и явлениями окружающего мира. Благодаря мышлению мы можем понять причинно – следственные связи, как в природе, так и в обществе.
В-третьих: мышление есть обобщенное познание действительности.
Функция мышления – расширение границ познания путем выхода за предмет чувственного восприятия.
Задача мышления – раскрытие отношений между предметами, выявление связей и отделение их от случайных совпадений. [3; 31]
Одной из наиболее распространенных в психологии является классификация видов мышления в зависимости от содержания решаемой задачи. При этом выделяют следующие виды мышления:
Наглядно-действительное мышление - процесс мышления представляет собой практическую преобразованную деятельность, осуществляемую человеком с реальными предметами.
Наглядно-образное мышление – один из видов мышления. Связано с представлением ситуаций и изменений в них. С помощью этого вида мышления наиболее полно воссоздается все многообразие различных фактических характеристик предмета. В образе может быть зафиксировано одновременно виденье предмета с нескольких точек зрения.
Функции образного мышления связаны с представлением ситуаций и изменений в них, которые человек хочет получить в результате своей деятельности, преобразующей ситуацию.
Словесно - логическое мышление – это умение оперировать абстрактными понятиями, это управляемое мышление, это мышление путем рассуждений.
Теоретическое понятийное мышление - это такое мышление, пользуясь которым человек в процессе решения задачи обращается к понятиям, выполняет действия в уме, непосредственно, не имея дела с опытом, получаемым при помощи органов чувств. Он обсуждает и ищет решение задачи сначала до конца в уме, выраженное в понятийной форме, суждениях, умозаключениях.
Понятие – это форма мышления, в которой отражаются общие и существенные свойства предметов и явлений. [11; 485]
Суждение – это форма мышления, при которой что–то утверждается или отрицается. [11; 676]
Умозаключение – это форма мышления, позволяющая сделать вывод из ряда суждений. [11; 723]
Теоретическое образное мышление - отличается тем, что материалом, который здесь использует человек для решения задачи, являются не понятия, суждения или умозаключения, а образы. Они или непосредственно извлекаются из памяти, или творчески воссоздаются воображением.
Дискурсивное мышление (рассудочное) - мышление, носящее рассудочный характер основанное на системе умозаключений, имеющее последовательный ряд логических звеньев, каждая из которых определяется предыдущим и обусловливает последующее звено. Дискуссионное мышление приводит к выводному знанию.
Алгоритмическое мышление - осуществляется в соответствии с установленной последовательностью элементарных операций, необходимых для решения задач данного класса.
Эвристическое мышление - творческое решение нестандартных задач.
Мышление практическое – мышление связано с постановкой целей, выработкой планов, проектов и часто развертывается в условиях дефицита времени.
Мышление теоретическое – мышление направлено на открытие законов, свойств объектов.
Мышление творческое – характеризуется созданием субъективно нового продукта и новообразованиями в самой познавательной деятельности по его созданию. [12; 225-226]
В процессе мыслительной деятельности человек познает окружающий мир с помощью особых умственных операций. Эти операции составляют различные взаимосвязанные, переходящие друг в друга стороны мышления. Основными мыслительными операциями являются:
Анализ - это расчленение предмета, мысленное или практическое, на составляющие его элементы с последующим их сравнением. [11; 24]
Синтез - есть построение целого из аналитически заданных частей. [11; 624]
Анализ дает ответ на вопрос: какая часть целого обладает определенными признаками. Результаты анализа объединяются, синтезируются. Синтез объединяет элементы, части, на основе установления существенных в определенном отношении связей между ними.
Классификация – заключается в отнесении единичного объекта или явления к соответствующей общей группе на основе существенных и общих признаков. [11; 238]
Абстракция - это выделение какой либо стороны или аспекта явления, которые в действительности как самостоятельные не существуют. Абстрагирование выполняется для более тщательного их изучения и, как правило, на основе предварительно произведенного анализа и синтеза. [11; 17]
Обобщение выступает как соединение существенного (абстрагирование) и связывание его с классом предметов и явлений. Понятие становится одной из форм мысленного обобщения. [11; 369]
Конкретизация выступает как операция обратная обобщению. Она проявляется в том, что из общего определения – понятия - выводится суждение о принадлежности единичных вещей и явлений определенному классу. [11; 249]
Более глубокое проникновение в суть вещей требует раскрытия их внутренних связей, закономерностей и существенных свойств. Оно выполняется при помощи операций мышления – анализа и синтеза.
На анализе и синтезе основаны все ступени мыслительного процесса.
Мыслительный процесс классификации также играет важную роль в развитии познавательной деятельности дошкольников: он закрепляет представления об отдельных предметах в их признаках и свойствах, об общих группах предметов, тем самым способствует развитию логического мышления, приводит знания в определенный порядок, подготовляя к систематическому школьному обучению. [7; 72]
В историческом развитии мышления и в развитии мышления ребенка различаются три сменяющие друг друга стадии - виды мышления:
1. наглядно - действенное (сенсомоторное) 0-4 лет
2. наглядно - образное 2-7 лет
3. абстрактно-логическое. 5-10лет
.Работа над развитием мышления ребенка, начиная с раннего детства, будет эффективной тогда, когда воспитатель включает подлинную умственную активность детей в любой вид их деятельности, в занятия и труд, в игры и наблюдения природы, в обсуждение поступка героя книги и в рисование с натуры или по представлению. Эта разнообразная деятельность детей требует всегда основного и общего процесса – анализа – синтеза.
Первый шаг в развитии основного мыслительного процесса: анализ – синтез. Все дальнейшее развитие умственной деятельности ребенка – усложнение и совершенствование этого процесса. Он становится все более и более дробным, тонким и обобщенным. [14; 194]
Развитие мышления (в плане освоения самого процесса) сказывается в том, что:
1. анализ становится все более дробным, а синтез все более обобщенным и точным;
2. один и тот же предмет подвергается анализу в разных направлениях;
3. ребенок овладевает анализом – синтезом как общим методом умственной деятельности. [14; 195]
Так же одной из форм мышления является речь. В речи мысль не только формируется, но и развивается.
Таким образом, мышление является процессом производства умозаключений с логическими операциями над ними.
Существуют различные методы, с помощью которых человек производит мыслительные операции и действия:
Метод проб и ошибок зарождается в раннем детстве, когда ребенок начинает познавать мир: трогает руками, пробует, смотрит – накапливает образы и понятия, ищет связи между своими действиями и их результатами.
Метод фокальных объектов – метод наделения обычных предметов совершенно необычными свойствами. Для тех, у кого развито воображение и фантазия.
Метод контрольных вопросов:
Осведомительные – цель: получение новой информации.
Контрольные – направленные на проверку знаний.
Наводящие – на решение проблемы, вопросы, помогающие найти сильную идею или понять ситуацию.
Проблемные или развивающие вопросы, побуждающие думать.
Занимательные вопросы провоцируют интерес у детей к ответу, к мыслительной деятельности.
Детское мышление проходит определенные этапы в своем развитии. Первым средством решения задач для маленького ребенка является практическое действие. Совершая различные манипуляции с предметом, ребенок либо получает желаемый результат, либо обращается за помощью к взрослым или вообще отказывается от дальнейших проб. Подобное мышление получило название наглядно – действенного, или практического: задача дана наглядно и решается руками, то есть практическим действием. «Мышление руками» не исчезает по мере взросления, а остается в резерве даже у взрослых, когда какую – то задачу они не могут решить в уме и начинают действовать путем проб и ошибок. К среднему дошкольному возрасту появляются задачи нового типа, где результат действия будет не прямым, а косвенным и для его достижения ребенку необходимо будет учитывать связи между двумя или несколькими явлениями, происходящими одновременно или последовательно. При решении задач с косвенным результатом дети четырех – пяти лет начинают переходить от внешних действий с предметами к действиям с образами этих предметов, совершаемым в уме. Так развивается наглядно – образное мышление, которое опирается на образы: ребенку необязательно брать предмет в руки, достаточно отчетливо представить его. В процессе наглядно – образного мышления идет сравнение зрительных представлений, вследствие чего задача решается. Возможность решения задач в уме возникает благодаря тому, что образы, которыми пользуется ребенок, приобретают обобщенный характер. То есть в них отображаются не все особенности предмета, а только те, которые существенны для решения определенной задачи. То есть в сознании ребенка возникают схемы, модели. Овладение моделями выводит на новый уровень способы получения детьми знаний. Если при словесном объяснении ребенок не всегда может понять, например, некоторые первичные математические действия, звуковой состав слова, то с опорой на модель он это сделает легко. Образные формы обнаруживают свою ограниченность, когда перед ребенком возникают задачи, которые требуют выделения таких свойств и отношений, которые нельзя наглядно представить. При решении задач без наглядного перехода действий, ребенок не может независимо рассмотреть наглядно происходящие с объектом перемены, например изменение формы, площади. Ведь для этого требуется переход от суждений на основе образов к суждениям на основе словесных понятий. Словесно – логическое мышление самое сложное, оно оперирует не конкретными образами, а сложными отвлеченными понятиями, выраженными словами. К шести годам понятия детей становятся глубже, полнее, обобщеннее, в них включаются все более существенные черты предмета, явления. Чтобы слова превратились в понятия, требуется специально организованное обучение ребенка со стороны взрослого. Систематическое овладение понятиями начинается в процессе школьного обучения. В старшем дошкольном возрасте начинается овладение действиями с числами и математическими знаками. Важно управлять этим и стремиться формировать у детей отвлеченное понятие числа как характеристики любых предметов, математических действий, без опоры на образы. Также ребенок овладевает некоторыми абстрактными понятиями: о временных отношениях, причине и следствии, пространстве. При этом понятия о конкретных предметах образуются легче и быстрее. На протяжении дошкольного возраста получают развитие и такие формы мыслительной деятельности, как суждение и умозаключение. В работе над развитием у детей логического мышления воспитатель должен своими вопросами, указаниями и пояснениями вести детей к выделению существенных частей и элементов целого соответственно той задаче, которую поставил перед собой. Показывая детям сразу же взаимосвязи, существующие между этими частями, воспитатель завершает свою работу обобщением, т.е. возвратом снова к целому, но уже понятому детьми более глубоко и полно. Это движение от целого к частям и их связям, а от них снова к целому – характернейшая черта высших форм мышления. [14; 200-205]
Получение знаний – обязательное условие развития мышления детей. Одни знания дети получают из общения со взрослыми, другие из собственной деятельности. Основу развития мышления составляет формирование и совершенствование мыслительных действий. Овладение мыслительными действиями в дошкольном возрасте происходит по принципу внешних ориентировочных действий. В зависимости от того, каковы эти внешние действия, формирующиеся мыслительные действия ребенка принимают либо форму действия с образами, либо форму действия, то есть наглядно – действенное мышление, либо со знаками – словами, числами, то есть логическое мышление. [9; 205]
Слово начинает использоваться как самостоятельное средство мышления по мере усвоения ребенком выработанных человечеством понятий – знаний об общих и существенных признаках предметов и явлений действительности, закрепленных в словах. Для того чтобы слово стало употребляться как самостоятельное средство мышления, позволяющее решать умственные задачи без использования образов, ребенок должен усвоить понятия, закрепленные в словах. [4; 30]
Обучение в детском саду должно быть направлено на воспитание у детей привычки полноценной логической аргументации окружающего. Опыт обучения свидетельствует о том, что развитию логического мышления дошкольников в наибольшей мере способствует изучение начальной математики. Для математического стиля мышления характерны четкость, краткость, расчлененность, точность и логичность мысли, умение пользоваться символикой. [2; 45]
Под математическим развитием дошкольников понимают качественные изменения в формах познавательной активности ребенка, которые происходят в результате формирования элементарных математических представлений и связанных с ними логических операций. [15; 5]
Занятие математикой приобретает особое значение в связи с развитием у детей познавательных интересов, умений проявлять волевые усилия в процессе решения математических задач.
На занятиях по математике в детском саду формируются простейшие виды практической и умственной деятельности детей.
Виды деятельности – способы обследования, счет, объективные последовательные действия, которые должен выполнить ребенок для усвоения знаний: поэлементное сравнение двух множеств, накладывание меры.
На основе практических действий у детей формируются такие мыслительные операции, как анализ, синтез, сравнение, обобщение. Важной задачей является развитие у них мышления и речи (овладение математической терминологией). Развитие начальных умений индуктивного и дедуктивного мышления. [15;5]
Любая математическая задача на смекалку, для какого бы возраста она ни предназначалась, несет в себе определенную умственную нагрузку, которая замаскирована занимательным сюжетом, внешними данными и условием задачи. [8; 3]
Различные умственные задачи: (составление фигур и их видоизменение, нахождение путь решения) – реализуются средствами игры в игровых действиях. Смекалка, находчивость, инициатива проявляются в активной умственной деятельности, основанной на непосредственном интересе. [15; 4]
Занимательность математическому материалу придают игровые элементы, содержащиеся в каждой задаче, логическом упражнении, развлечении.
Разнообразный элементарный занимательный материал можно классифицировать, выделив в нем условно 3 основные группы:
· Развлечения
· Математические игры и задачи
· Развивающие игры и упражнения (дидактические)
Математические развлечения: головоломки, ребусы, лабиринты, игры на пространственное преобразование и др. они интересны по содержанию, занимательны по форме, отличаются необычностью решения, парадоксальностью результата.
Математические игры: это игры, в которых смоделированы математические построения, отношения, закономерности. Для нахождения ответа необходим предварительный анализ условий, правил, содержания игры или задачи. По ходу решения требуется применение математических методов и умозаключений. Разновидностью математических игр и задач являются логические игры, задачи и упражнения. Они направлены на тренировку мышления при выполнении логических операций и действий.
Дидактические игры и упражнения: они направлены на развитие у детей разного возраста логического мышления, пространственных представлений, дают возможность упражнять ребят в счете, вычислениях. [8; 5-6]
Используется занимательный материал с целью формирования представлений, ознакомления с новыми сведениями. При этом непременным условием является применение системы игр и упражнений.
Когда занимательная задача доступна ребенку, у него складывается положительное эмоциональное отношение к ней, что и стимулирует мыслительную активность. При этом дети пользуются двумя видами поисковых проб: практическими (действия в перекладывании, подборе) и мыслительными (обдумывание хода, предугадывание результата, предположение решения). В ходе поиска гипотез, решения дети проявляют и догадку, т.е. приходят к правильному решению. Практическими пробами пользуются дети 5 – 6 лет, а дети 7 лет осуществляют поиск путем сочетания мысленных и практических проб. [15; 6]
Н.А. Непомнящая определила следующие задачи математического развития детей старшего дошкольного возраста:
1. обучение обобщенным способам, формирование простейших абстрактных математических представлений, использование моделей и знаков.
2. передача определенных знаний и способов решения задач.
3. формирование психологических механизмов, которые обеспечивают в максимальной степени успешность обучения, возможности самостоятельности в дальнейшей учебной деятельности и практике применения знаний.
4. формирование промежуточного уровня знаний и действий, который и должен обеспечить связь математических абстракций с конкретной действительностью. [10; 182]
Таким образом, ребенка дошкольного возраста необходимо научить сравнивать, обобщать, анализировать, организуя различные виды деятельности. Когда дошкольника побуждают подробно, развернуто объяснять явления и процессы в природе, социальной жизни, то рассуждение превращается в способ познания и решения интеллектуальных задач. Усвоение системы знаний также позволяет дошкольнику более эффективно решать интеллектуальные проблемы.
Игры математического содержания помогают воспитывать у детей познавательный интерес, способность к исследовательскому и творческому поиску, желание и умение учиться. Необычная, с элементами проблемности, присущая занимательной задаче, интересна детям. Дети начинают осознавать, что в каждой из занимательных задач заключена какая-либо хитрость, выдумка, забава. Найти, разгадать ее невозможно без сосредоточенности, напряженного обдумывания, постоянного сопоставления цели с полученным результатом.
Глава 2. Педагогические условия развития мышления у детей шестого года жизни посредством занимательных задач
2.1 Особенности развития мышления у детей шестого года жизни посредством занимательных задач
С целью выявления особенностей развития мышления у детей шестого года жизни посредством занимательных задач нами был проведен констатирующий эксперимент.
Задачи констатирующего эксперимента:
1. Выявить уровень интереса к игровым занимательным задачам по математике у детей шестого года жизни.
2. Выявить уровень развития мыслительных процессов: обобщения, классификации, анализа у детей шестого года жизни.
3. Выявить уровень развития наглядно – образного и зачатков словесно-логического мышления у детей шестого года жизни.
Исследование проводилось на базе МДОУ № 3, в группе детей шестого года жизни с 23. 03. 2009 по 25.03. 2009 г. В эксперименте участвовало 10 человек (см. Таблицу 1).
Таблица 1.
Список детей экспериментальной группы
| № | Имя ребенка | Возраст |
| 1 | Данил К. | 5 лет 3мес. |
| 2 | Гоша И. | 5 лет 3мес. |
| 3 | Ваня Б. | 5 лет 1мес. |
| 4 | Денис Ш. | 5лет 5мес. |
| 5 | Евгений Н. | 5лет 5мес. |
| 6 | Катя П. | 5лет 3мес. |
| 7 | Полина В. | 5лет 3мес. |
| 8 | Алина К. | 5лет 4мес. |
| 9 | Зоя Р. | 5лет 5мес. |
| 10 | Настя Д. | 5лет 5мес. |
Для решения поставленных задач нами был проведен трехсерийный эксперимент.
В первой серии эксперимента у детей выявляли уровень интереса к игровым занимательным задачам. Для этого нами была использована методика «Выбор» (Н.Соколовой). Ребенку предлагалось в течение трех дней выбрать, чем он хочет заниматься: играть в настольную игру, читать или решать задачи. Каждый выбор оценивался в 1 балл. Затем подсчитывалось количество выборов по каждому виду деятельности.
Высокий уровень интереса к игровым занимательным задачам – ребенок выбирает занятия математическими задачами 3 раза.
Средний уровень интереса к игровым занимательным задачам - ребенок выбирает занятия математическими задачами 2 раза.
Низкий уровень интереса к игровым занимательным задачам - ребенок выбирает занятия математическими задачами 1 раз или не выбирает ни разу.
Результаты исследования по методике «Выбор» представлены в таблице 2, протокол в Приложении 1.
Таблица 2.
Уровень интереса к занимательным математическим задачам
| № п/п | Имя ребенка | Настольная игра | Чтение | Занимательные задачи | уровень |
| 1 | Данил К. | 0 | 0 | 1 | Низкий |
| 2 | Гоша И. | 2 | 0 | 0 | Низкий |
| 3 | Ваня Б. | 1 | 1 | 1 | Низкий |
| 4 | Денис Ш. | 3 | 0 | 0 | Низкий |
| 5 | Евгений Н. | 0 | 0 | 3 | Высокий |
| 6 | Катя П. | 1 | 2 | 0 | Низкий |
| 7 | Полина В. | 0 | 2 | 0 | Низкий |
| 8 | Алина К. | 3 | 0 | 0 | Низкий |
| 9 | Зоя Р. | 0 | 0 | 3 | Высокий |
| 10 | Настя Д. | 1 | 1 | 1 | Низкий |
детский мышление игровой задача

Рис.1. Уровень интереса к занимательным математическим задачам у детей шестого года жизни
Проведенное исследование показало (Рис.1), что:
Низкий уровень интереса к занимательным математическим задачам наблюдается у 80 % детей; средний уровень не выявлен; высокий уровень – у 20% детей.
Во второй серии констатирующего эксперимента у детей выявляли уровень развития мыслительных операций: обобщения, классификации, анализа.
Для оценки умственных операций анализа, обобщения и классификации использовалась методика «Лишний предмет» (Л.Парамоновой).
Ребенку последовательно предъявляли 6 карточек, на которых изображены различные предметы: по четыре на каждой карточке (см. Приложение 1). Вначале ребенку показывали первую (тренировочную) карточку и объясняли, что из четырех предметов один – лишний. Необходимо определить его и объяснить свое решение. После этого предлагали ребенку подумать и сказать, как можно назвать оставшиеся три предмета одним словом.
Результаты оценивались в баллах (по каждому критерию отдельно):
Анализ:
3 балла – ребенок смог самостоятельно определить лишний предмет и объяснить свое решение;
2 балла – ребенок определил предмет с подсказки взрослого, в объяснении решения были затруднения;
1 балл – ребенок не смог определить лишний предмет и обосновать решение.
Обобщение и классификация:
3 балла – ребенок смог самостоятельно обобщить и сказать правильный ответ;
2 балла – ребенок обобщил и сказал ответ с подсказки взрослого;
1 балл – ребенок не смог обобщить и сказать правильного ответа.
Полученные результаты развития мыслительных процессов представлены в таблице 3, протокол в Приложении 2.
Таблица 3.
Уровень развития мыслительных операций у детей шестого года жизни
| № п/п | Имя ребенка | Анализ | Обобщение и классификация | Сумма баллов | Средний балл | Уровень | ||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
4 |
5 |
6 |
|||||
| 1 | Данил К. | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 36 | 3 | В |
| 2 | Гоша И. | 3 | 3 | 3 | 0 | 0 | 3 | 3 | 3 | 3 | 0 | 0 | 3 | 24 | 2 | С |
| 3 | Ваня Б. | 3 | 3 | 3 | 3 | 3 | 0 | 2 | 3 | 3 | 3 | 3 | 0 | 29 | 2,4 | В |
| 4 | Денис Ш. | 3 | 0 | 3 | 3 | 3 | 3 | 3 | 0 | 3 | 3 | 3 | 2 | 29 | 2,4 | В |
| 5 | Евгений Н. | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 36 | 3 | В |
| 6 | Катя П. | 3 | 3 | 3 | 0 | 3 | 3 | 1 | 3 | 3 | 0 | 3 | 3 | 28 | 2,3 | С |
| 7 | Полина В. | 3 | 3 | 3 | 3 | 0 | 3 | 3 | 3 | 3 | 3 | 0 | 3 | 25 | 2,1 | С |
| 8 | Алина К. | 3 | 3 | 0 | 3 | 3 | 3 | 2 | 3 | 0 | 3 | 3 | 3 | 29 | 2,4 | В |
| 9 | Зоя Р. | 3 | 3 | 0 | 3 | 3 | 3 | 0 | 3 | 0 | 3 | 3 | 3 | 27 | 2,3 | С |
| 10 | Настя Д. | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 3 | 3 | 1 | 3 | 2 | 31 | 2,6 | В |
Исходя из этих показателей, мы определили уровни развития мыслительных операций: обобщения, классификации, анализа:
Высокий уровень (3 – 2,4 балла) – у ребенка развиты процессы анализа: он безошибочно находит лишний предмет, обосновывает свой выбор; самостоятельно обобщает и классифицирует предметы по определенным признакам;
Средний уровень (2,3 – 1,7 балла) – у ребенка развиты процессы анализа: он находит лишний предмет, но делает это при помощи взрослого, не всегда может обосновать свой выбор; обобщает и классифицирует предметы по определенным признакам, прибегая к помощи взрослого.
Низкий уровень (1,6 – 1 балл) – у ребенка плохо развиты процессы анализа: он не может определить лишний предмет; затрудняется в обобщении и классификации предметов по определенным признакам даже при подсказке взрослого.
Проведенное исследование показало (Рис.2), что: высокий уровень наблюдается у 60% детей; средний уровень у 40% детей; низкий уровень не выявлен.
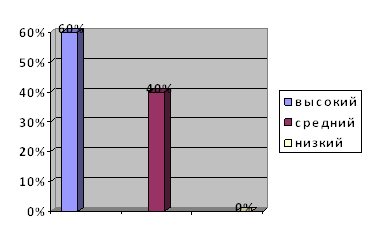
Рис. 2. Уровень развития мыслительных операций: обобщения, анализа и классификации у детей шестого года жизни
В третьей серии констатирующего эксперимента у детей выявляли уровень развития наглядно – образного и зачатков словесно-логического мышления у детей шестого года жизни.
Работа проводилась в два этапа: на первом этапе выявляли уровень зрительного восприятия; на втором - зачатки словесно – логического мышления.
I этап. Для выявления зрительного восприятия использовалась методика «Найди 10 отличий».
Ребенку предлагались две картинки с изображением предмета (см. Приложение 2.2). Ребенку необходимо было найти различия в изображении предмета.
Результаты оценивались в баллах:
3 балла – ребенок нашел 8-10 отличий.
2 балла – ребенок нашел 5-7 отличий.
1 балл – ребенок нашел 4 отличия и меньше.
II этап. Для выявления зачатков словесно – логического мышления использовалась методика «Что за чем?».
Ребенку предлагались три картинки с изображением трех стадий действий (см. Приложение 3.3). Необходимо было разложить картинки в логической последовательности и составить маленький рассказ из 3 – 4 предложений по этим картинкам.
Задание оценивалось по 2 критериям:
1. Умение раскладывать по порядку:
3 балла – разложил правильно, не думая долго;
2 балла – разложил правильно, но долго думал, сомневался;
1 балл – разложил неправильно.
2. Составление рассказа:
3 балла – ребенок составил рассказ из 4 и более предложений;
2 балла – ребенок составил рассказ из 1 – 3 предложений;
1 балл – ребенок не смог составить рассказ
Полученные результаты уровня развития наглядно – образного мышления заносились в таблицу 4, протокол в Приложении 3.
Таблица 4.
Уровень развития наглядно – образного и зачатков словесно-логического мышления у детей шестого года жизни
| № п/п | Имя ребенка | Зрительное восприятие | Зачатки логического мышления | Сумма баллов | Средний балл | уровень | |
| 1 | 2 | ||||||
| 1 | Данил К. | 2 | 3 | 2 | 7 | 2,3 | Средний |
| 2 | Гоша И. | 3 | 2 | 2 | 7 | 2,3 | Средний |
| 3 | Ваня Б. | 2 | 3 | 3 | 8 | 2,6 | Высокий |
| 4 | Денис Ш. | 1 | 3 | 2 | 6 | 2 | Средний |
| 5 | Евгений Н. | 3 | 3 | 2 | 8 | 2,6 | Высокий |
| 6 | Катя П. | 2 | 2 | 2 | 6 | 2 | Средний |
| 7 | Полина В. | 2 | 3 | 2 | 7 | 2,3 | Средний |
| 8 | Алина К. | 2 | 1 | 2 | 5 | 1,6 | Низкий |
| 9 | Зоя Р. | 3 | 1 | 3 | 7 | 2,3 | Средний |
| 10 | Настя Д. | 2 | 1 | 1 | 4 | 1,3 | Низкий |
Исходя из этих показателей, мы определили уровни развития наглядно-образного и зачатков словесно-логического мышления.
Высокий уровень (3 – 2,4 балла) – ребенок смог найти 8-10 отличий на картинках; не долго думая правильно, в логической последовательности разложил картинки; придумал по ним рассказ из четырех и более предложений.
Средний уровень (2,3 – 1,7 балла) – ребенок смог найти 5-7 отличий на картинках; разложил картинки правильно, но долго думал, сомневался в своем решении; составил рассказ по картинкам из 1-3 предложений.
Низкий уровень (1,6 – 1 балл) – ребенок смог найти 4 и менее отличий на картинках; не смог определить логическую последовательность и поэтому не смог разложить картинки правильно; также не смог составить рассказ.
Проведенное исследование показало (Рис.3), что: высокий уровень развития наглядно – образного и зачатков словесно-логического мышления наблюдается у 20% детей; средний уровень - у 60% детей; низкий уровень - у 20% детей.
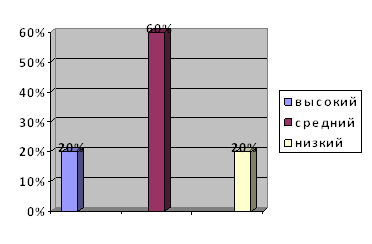
Рис. 3. Уровень развития наглядно – образного и зачатков словесно-логического мышления у детей шестого года жизни
Исходя из результатов констатирующего эксперимента по всем трем сериям, мы определили общий уровень развития мышления у детей шестого года жизни посредством занимательных задач.
Результаты представлены в таблице 4.
Высокий уровень (3 – 2,4 балла) – у ребенка устойчивый интерес к занимательным математическим задачам. Развиты процессы анализа: он безошибочно находит лишний предмет, обосновывает свой выбор; самостоятельно обобщает и классифицирует предметы по определенным признакам. Находит в двух изображениях 8-10 отличий. Не долго думая, раскладывает картинки в правильной последовательности, без затруднений придумывает рассказ из четырех и более предложений.
Средний уровень (2,3 – 1,7 балла) – у ребенка имеется интерес к занимательным математическим задачам. Процессы анализа развиты, но при определении лишнего предмета ребенку требуется помощь взрослого; также обобщает и классифицирует при помощи взрослого. Находит в двух изображениях 5-7 отличий. Ребенок способен определить логическую последовательность расположения картинок, но ребенок долго думает и сомневается в своем решении. Способен составить рассказ из 1-3 предложений.
Низкий уровень (1,6 – 1 балл) – у ребенка низкий уровень интереса к занимательным математическим задачам. Процессы анализа не развиты: ребенок не может найти лишний предмет, не способен обосновать свой выбор; не может обобщить и классифицировать предметы по определенным признакам. Находит 4 отличия и менее. Ребенок не способен определить логическую последовательность расположения картинок. Не может составить рассказа.
Таблица 4.
Уровень развития мышления у детей шестого года жизни посредством занимательных задач
| № п/п | Имя ребенка | 1 серия | 2 серия | 3 серия | Сумма баллов | Средний балл | Уровень |
| 1 | Данил К. | 1 | 3 | 2,3 | 6,3 | 2,1 | Средний |
| 2 | Гоша И. | 1 | 2 | 2,3 | 5,3 | 1,8 | Средний |
| 3 | Ваня Б. | 1 | 2,4 | 2,6 | 6 | 2 | Средний |
| 4 | Денис Ш. | 1 | 2,4 | 2 | 5,4 | 1,8 | Средний |
| 5 | Евгений Н. | 3 | 3 | 2,6 | 8,6 | 2,9 | Высокий |
| 6 | Катя П. | 1 | 2,3 | 2 | 5,3 | 1,8 | Средний |
| 7 | Полина В. | 1 | 2,1 | 2,3 | 5,4 | 1,8 | Средний |
| 8 | Алина К. | 1 | 2,4 | 1,6 | 5 | 1,6 | Низкий |
| 9 | Зоя Р. | 3 | 2,3 | 2,3 | 7,6 | 2,5 | Высокий |
| 10 | Настя Д. | 1 | 2,6 | 1,3 | 4,9 | 1,6 | Низкий |
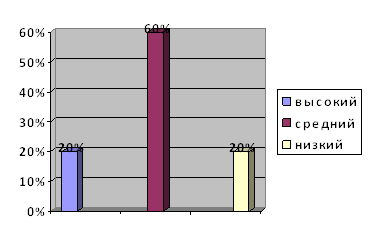
Рис 4. Уровень развития мышления у детей шестого года жизни посредством занимательных задач
Таким образом, проведенное исследование показало (рис 4), что: высокий уровень развития мышления у детей шестого года жизни посредством занимательных задач наблюдается у 20% детей; средний уровень - у 60% детей; низкий уровень - у 20% детей.
Проведенное нами исследование, которое было направлено на выявление уровня интереса детей к занимательным математическим задачам, уровня развития мыслительным процессов – анализа, обобщения и классификации; развития зрительного восприятия; зачатков словесно – логического мышления показало, что всего лишь у 20% детей шестого года жизни мышление на высоком уровне, то есть, развиты процессы анализа, классификации и обобщения - ребенок самостоятельно безошибочно находит лишний предмет, обосновывает свой выбор; самостоятельно обобщает и классифицирует предметы по определенным признакам. Развито зрительное восприятие - находит в двух изображениях 8-10 отличий. Присутствуют зачатки словесно – логического мышления - не долго думая, раскладывает картинки в правильной последовательности, без затруднений придумывает рассказ из четырех и более предложений. Лишь у 20% детей имеет высокий интерес к математическим задачам.
У 60% детей шестого года жизни мышление находится на среднем уровне, то есть процессы анализа развиты, но при определении лишнего предмета ребенку тре взрослого; также обобщает и классифицирует при помощи взрослого. Имеются некоторые трудности в зрительном восприятии - находит в двух изображениях 5-7 отличий. Имеются предпосылки к словесно – логическому мышлению - ребенок способен определить логическую последовательность расположения картинок, но долго думает и сомневается в своем решении. Способен составить рассказ из 1-3 предложений. Не выявлен средний уровень интереса к математическим задачам.
У 20% детей шестого года жизни мышление на низком уровне, то есть процессы анализа не развиты: ребенок не может найти лишний предмет, не способен обосновать свой выбор; не может обобщить и классифицировать предметы по определенным признакам. Имеются значительные проблемы со зрительным восприятием - находит на двух изображениях 4 отличия и менее. Зачатки словесно – логического мышления не выявлены - ребенок не способен определить логическую последовательность расположения картинок. Не может составить рассказа. У 80% детей выявлен низкий уровень к математическим задачам.
Мыслительная операция анализ – у 90% детей на высоком уровне. Ребенок самостоятельно безошибочно определяет лишний предмет и четко уверенно обосновывает свой ответ. У 10% на среднем уровне - ребенок определил лишний предмет с подсказки взрослого, при объяснении решения имелись затруднения.
Мыслительные операции обобщения и классификация – у 30% детей на высоком уровне. Эти дети могут самостоятельно обобщить и сказать правильный ответ. У 70% на среднем уровне. Дети обобщали и называли ответ с подсказки взрослого.
Зрительное восприятие – у 30% на высоком уровне. Детям не составило особого труда найти 8-10 отличий на двух изображениях. У 60% средний уровень. Дети долго рассматривали изображения и нашли 5-7 отличий. У 10% низкий уровень. Ребенок отвлекался, не мог сосредоточиться и с большим трудом нашел 4 отличия и менее.
Зачатки словесно – логического мышления:
1. умение раскладывать по порядку – у 50% детей на высоком уровне.
Дети разложили картинки правильно, не думая долго; у 20% на среднем уровне. Разложили правильно, но долго думали, сомневались; у 30% на низком уровне. Дети не смогли правильно разложить картинки.
2. умение составить рассказ – у 20% детей на высоком уровне.
Дети составили логически правильный рассказ из 4 и более предложений.
У 10% низкий уровень. Ребенок не способен составить рассказ. У 70% средний уровень. Дети смогли составить рассказ, но очень долго думали над каждым предложением, составили 1-3 предложения.
Таким образом, формирующая работа, главным образом, должна быть направлена на формирование интереса к занимательным задачам, развитие умения осуществлять последовательные умственные действия: анализировать, сравнивать, обобщать по признаку, целенаправленно думать. На этой основе будут развиваться зрительное восприятие. Необходимо учить детей искать путь решения, учиться планировать ход мысли, рассуждать, объясняя способ и путь решения. Игровые задания должны быть направлены на развитие мыслительных операций, смекалки, находчивости, сообразительности и логического мышления.
2.2 Педагогические условия развития мышления посредством игровых занимательных задач у детей шестого года жизни
Целью формирующей работы является развитие мышление у детей шестого года жизни посредством игровых занимательных задач.
Задачи:
1. Разработать систему игр и упражнений по развитию мышления у детей шестого года жизни посредством игровых занимательных задач.
2. Определить эффективные педагогические условия развития мышления у детей шестого года жизни посредством игровых занимательных задач.
Работу необходимо проводить в три этапа.
Целью первого этапа является развитие интереса к занимательной математике у детей шестого года жизни.
Задачи:
1. Развитие интереса к занимательным математическим задачам.
2. Развитие умения планировать ход мысли, рассуждать, объясняя способ и путь решения задачи.
На данном этапе проводятся игры и упражнения на решение простых задач на смекалку геометрического характера – головоломок с палочками. Важно, чтобы каждый ребенок смог решить задачу, почувствовал успех от решения и захотел решать более сложные задачи. Основная цель – учить детей приемам самостоятельного поиска решения задач, не предлагая готовых образцов.
Решение задач на смекалку используется в одной из частей занятия по математике, а так же вне занятий по математике, как в индивидуальной работе, так и в самостоятельной. На этом этапе детям даются задачи на составление заданной фигуры из определенного количества счетных палочек.
На первом занятии детей упражняют в составлении геометрических фигур на плоскости стола, анализе и обследовании их зрительно-осязательным способом (см. Приложение 4).
Детям предлагаются следующие задания:
1. Составить квадрат и треугольник маленького размера.
2. Составить маленький и большой квадраты.
3. Составить прямоугольник, верхняя и нижняя стороны которого будут равны 3 палочкам, а левая и правая – 2.
Целью второго занятия является упражнение детей в самостоятельных поисках путей составления фигур на основе предварительного обдумывания хода решения (см. Приложение 5).
Детям предлагаются следующие задания:
1. Отсчитать 10 палочек и составить из них 3 равных квадрата. Подумать, как надо составлять, и рассказать.
2. Из 5 палочек составить квадрат и 2 равных треугольника. Сначала рассказать, а затем составить.
3. Из 9 палочек составить квадрат и 4 треугольника. Подумать и сказать, как надо составлять.
В индивидуальной работе вне занятий для закрепления пройденного материала детям предлагаются следующие задания (см. Приложение 6).
1. Из 10 палочек составить 2 квадрата – маленький и большой.
2. Из 9 палочек составить 5 треугольников.
3. Составить 2 равных квадрата из 7 палочек.
Взрослый организует совместную игру с ребенком или подгруппой детей, стимулирует проявления самостоятельности, поощряет стремление достичь результата.
По мере усвоения детьми способов решения задач воспитатель оформляет в группе уголок занимательной математики. Художественное оформление уголка должно привлекать и заинтересовывать детей. Для этого можно использовать геометрические орнаменты или сюжетные изображения из геометрических фигур. Наборы счетных палочек ставят на видное место, чтобы ребенок по желанию мог воспользоваться ими.
Таким образом, на первом этапе дети, практически действуя с палочками, ищут путь решения, учатся планировать ход мысли, рассуждать, объясняя способ и путь решения. Интерес поддерживается желанием достичь успеха.
Целью второго этапа является развитие мышления у детей шестого года жизни.
Задачи:
1. Развитие смекалки и находчивости.
2. Развитие умения осуществлять последовательные умственные действия: анализировать, сравнивать, обобщать по признаку, целенаправленно думать.
3. Развивать логическое мышление и сообразительность.
Для решения первой задачи используются игры и упражнения с палочками на изменение фигур (см. Приложение 7). Данные задания даются на занятии по математике и вне занятий, с целью закрепления практических действий с палочками и поиска самостоятельного решения, а также создания ситуации успеха, что в свою очередь будет поддерживать интерес к занимательным задачам.
Детям предлагаются задания (см. Приложение 8):
1. В фигуре, состоящей из 5 квадратов, убрать 4 палочки, оставив один прямоугольник.
2. В фигуре, состоящей из 6 квадратов, убрать 2 палочки, чтобы осталось 4 равных квадрата.
3. Составить домик из 6 палочек, а затем переложить 2 палочки так, чтобы получился флажок.
На первом занятии для развития смекалки и находчивости применяются задачи – шутки и занимательные вопросы, которые используются в начале занятия по математике. Их целью является приобщение детей к активной умственной деятельности, выработке умения выделять главные свойства, математические отношения. Важно, чтобы ребенок понял шутку, выделил ее. На протяжении занятия, особенно при переходе от одной его части к другой, смене деятельности, занимательные вопросы и задачи - шутки могут служить средством активации, переключения внимания детей, интеллектуального отдыха (см. Приложение 9).
Детям предлагаются следующие задания:
1. Ты да я, да мы с тобой. Сколько нас всего? (Двое).
2. Если курица стоит на одной ноге, то она весит 2 кг. Сколько будет весить курица, если будет стоять на двух ногах? (2 кг.)
3. У трех братьев по одной сестре. Сколько всего детей в семье? (Четверо).
На втором занятии используются игры и упражнения на нахождение отличительных признаков, на поиск недостающих в ряду фигур путем зрительного и мыслительного анализа. Для успешного решения подобных задач необходимо развивать у детей обобщать ряд фигур по выделенным признакам, сопоставлять обобщенные признаки одного ряда с признаками другого (см. Приложение 10).
Детям предлагаются задания:
1. Продолжить ряд изображений.
2. Чем отличается одна картинка от другой?
3. Найди 2 одинаковых предмета?
Таким образом, на втором этапе дети учатся осуществлять последовательные умственные действия: анализировать, сравнивать, обобщать по признаку, целенаправленно думать. По мере освоения практических действий с палочками в уголок математики добавляются игры для развития логического мышления («Найди отличия», «Что лишнее»), головоломки (на палочках и механические); логические задачи и кубики, лабиринты; игры на составление целого из частей, игры на передвижение. Для стимулирования коллективных игр, творческой деятельности дошкольников необходимо использовать магнитные доски, фланелеграфы с наборами фигур, счетных палочек.
Целью третьего этапа является развитие у детей творчества и самостоятельности в решении занимательных задач.
Основная цель – выявить умения самостоятельно решать занимательные математические задачи. Для этого целесообразно провести математический КВН (см. Приложение 11). В математическом КВН будут использованы задания на составление геометрических фигур из палочек, на нахождение недостающей фигуры, задания на логику и зрительное восприятие и на знание числового ряда. В ходе проведения КВН будут выявлены знания, которые дети получали на занятиях по математике и в индивидуальной работе; также будет выявлен уровень коллективных навыков решения задач; уровень смекалки и находчивости.
Таким образом, формирующая работа должна быть направлена на развитие интереса к игровым занимательным задачам; развитие умения планировать ход мысли, рассуждать; развитие смекалки и находчивости; развитие умения осуществлять последовательные умственные действия: анализировать, сравнивать, обобщать по признаку, целенаправленно думать; развитие логического мышления и сообразительности.
Развитие мышления у детей шестого года жизни посредством занимательных задач будет эффективным, если:
1. Использовать в работе с детьми шестого года жизни занимательные и доступные по возрасту игровые математические задачи.
2. Игровые занимательные задачи вводить в обучение детей постепенно, в порядке усложнения трудности их решения.
3. Учить детей приемам самостоятельного поиска решения задач, не предлагая готовых образцов.
4. Дети будут решать занимательные задачи не только на занятиях, но и вне занятий.
Заключение
Мышление соотносит данные ощущений и восприятий, сопоставляет, сравнивает, различает и раскрывает отношения. Мышление глубже познает сущность окружающего мира, отражает бытие в его связях и отношениях.
Игры и задачи с математическим содержанием способствуют всестороннему развитию и воспитанию: активизируют умственную деятельность, заинтересовывают математическим материалом, увлекают и развлекают детей, развивают ум, расширяют и углубляют математические представления, закрепляют полученные знания и умения, упражняют в применении их в других видах деятельности. Когда занимательная задача доступна ребенку, у него складывается положительное эмоциональное отношение к ней, что и стимулирует мыслительную активность.
Данные констатирующего эксперимента показали, что 80% детей низкий уровень интереса к занимательной математике и лишь у 20% высокий; у 60% детей мыслительные операции: анализ, сравнение, обобщение на высоком уровне, низкого уровня развития мыслительных операций нет; у 50% детей присутствуют зачатки словесно-логического мышления, у 30% - нет зачатков логического мышления.
Формирующая работа должна быть направлена на повышение уровня интереса к игровым занимательным задачам, на развитие основных мыслительных операций: сравнения, анализа, классификации; на формирование словесно-логического мышления.
Таким образом, развитие мышления у детей шестого года жизни посредством занимательных задач будет эффективным, если:
1. Использовать в работе с детьми шестого года жизни занимательные и доступные по возрасту игровые математические задачи.
2. Игровые занимательные задачи вводить в обучение детей постепенно, в порядке усложнения трудности их решения.
3. Учить детей приемам самостоятельного поиска решения задач, не предлагая готовых образцов.
4. Дети будут решать занимательные задачи не только на занятиях, но и вне занятий.
Библиография
1. Венгер Л.А., Психология: Учеб. пособие для учащихся пед. уч-щ по спец. № 2002 «Дошкольное воспитание» и № 2010 «Воспитание в дошк. учреждениях» [Текст] / Мухина В.С. – М.: Просвещение, 1988. – 336 с. 5000 экз. ISBN 5-09-000760-8.
2. Венгер Л.А. Игры и упражнения по развитию умственных способностей у детей дошкольного возраста: Кн. для воспитателя дет. сада [Текст] / О.М. Дьяченко, Р.И. Говорова, Л.И. Цеханская – М.: Просвещение, 1989. – 127с. 1500 экз. ISBN 5-09-001129-Х.
3. Венгер Л.А. Развитие мышления дошкольника [Текст] – М.: «Дошкольное воспитание» 1974, №7. 260 с. 42000 экз. ISSN 0012-556Х.
4. Глуховеря Н.П. Познавательная деятельность детей, ее особенности [Текст] – М.: «Дошкольное воспитание» 1976, № 11. 42000 экз. ISSN 0012-556Х.
5. Жикалкина Т.К. Игровые занимательные задачи для дошкольников [Текст] – М.: Просвещение, 1990. 89 с. 5000 экз. ISBN 987-5-7659Х.
6. Кордуэлл М. Психология. А-Я: Словарь-справочник /Пер.с англ. К.С. Ткаченко [Текст] – М.: ФАИР-ПРЕСС, 1999. – 448с. 20000 экз. ISBN 5-8183-0105-2.
7. Люблинская А.А. О некоторых особенностях развития логического мышления у детей [Текст] – М.: «Дошкольное воспитание» 1960, № 7. 42000 экз. ISSN 0012-556Х.
8. Михайлова З.А. Игровые занимательные задачи для дошкольников: Кн. для воспитателя дет. сада [Текст] – 2-е изд., дораб. – М.: Просвещение, 1990. – 94 с. 10000 экз. ISBN 5-09-001638-0.
9. Мухина В.С. Психология дош-ка. Учеб. пособие для студентов пед. ин-тов и учащихся пед. училищ [Текст] / Под ред. Л.А. Венгера. М., Просвещение, 1975. – 239с. 3000 экз. ISBN 5-09-00247-9.
10. Непомнящая В.С. Психологический анализ обучения детей 3-7 лет (на материале математики) [Текст] – М.: Просвещение, 1983. 270 с. 40000 экз. 371.21 У-561.
11. Ожегов С.И. Словарь русского языка: Ок. 57000 слов [Текст] / Под ред. чл.-корр. АН СССР Н.Ю. Шведовой. – 17-е изд., стереотип. – М.: Рус. яз., 1985. – 797 с. 195000 экз. ББК 81.2Р-4 0-45.
12. Петровский А.В. Психология словарь [Текст] / Ярошевский М.Г. – М.: Просвещение, 1990. 585 с. 5000 экз. ISBN 5-769-0465-Х.
13. Поддъяков Н.Н. Умственное воспитание дошкольника [Текст] – М. 1972. 288 с. 40000 экз. 372.21 У-563.
14. Урунтаева Г.А. Дошкольная психология: Учеб. пособие для студ. сред. пед. учеб. заведений [Текст] – 5-е изд., стереотип. – М.: Издательский центр «Академия», 2001 – 336с. 5000 экз. ISBN 5-7695-0034-4.
15. Щербакова Е.И. Методика обучения математике в детском саду: Учеб. пособие для студ. дошк. отд-ний и фак. сред. пед. учеб. заведений [Текст] – 2-е изд., стереотип. – М.: Издательский центр «Академия», 2000 – 272 с. 25000 экз. ISBN 5-7695-0522-2.