Курсовая работа: Движение тела, брошенного под углом к горизонту: программное обеспечение
Курсовая работа по дисциплине
Высокоуровневые методы информатики и программирования
на тему:
Движение тела, брошенного под углом к горизонту: программное обеспечение
Содержание
Введение
1. Описание предметной области
1.1 Предметная область
1.1.1 Развитие направления
1.1.2 Движение тела, брошенного под углом к горизонту
2. Рабочий проект
2.1 Общие сведения о работе программе (на чем написано, какие технологии использованы)
2.2 Основные процедуры/классы системы
2.3 Инсталляция программного продукта
2.4 Руководство пользователя
2.5 Сообщения системы
2.6 Требования к техническому и программному обеспечению
2.6.1 Требования к программному обеспечению
2.6.2 Требования к техническому обеспечению
2.7 Тестирование системы
Заключение
Список литературы
Приложение 1. Блок-схема
Приложение 2. Программа на оптическом носителе
Введение
Меха́ника (греч. μηχανική — искусство построения машин) — область физики, изучающая движение материальных объектов и взаимодействие между ними. Важнейшими разделами механики являются классическая механика и квантовая механика.
Движение тела, брошенного под углом к горизонту, необходимо рассматривать, как криволинейное движение, которое в свою очередь является одним из разделов механики.
Целью данной курсовой работы является закрепление практических навыков программирования и разработка программы, реализующей модель движения тела, брошенного под углом к горизонту.
Практической значимостью данной работы является автоматизация расчетов физических величин движения тела, брошенного под углом к горизонту и, как следствие, экономия времени преподавателей или студентов при решении указанной задачи.
движение тело программный обеспечение
1. Описание предметной области
1.1 Предметная область
Меха́ника (греч. μηχανική — искусство построения машин) — область физики, изучающая движение материальных объектов и взаимодействие между ними. Важнейшими разделами механики являются классическая механика и квантовая механика.
Движение тела, брошенного под углом к горизонту, необходимо рассматривать, как криволинейное движение, которое в свою очередь является одним из разделов механики.
1.1.1 Развитие направления
Изучение особенностей такого движения началось довольно давно, еще в XVI веке и было связано с появлением и совершенствованием артиллерийских орудий.
Представления о траектории движения артиллерийских снарядов в те времена были довольно забавными. Считалось, что траектория эта состоит из трех участков: А - насильственного движения, В - смешанного движения и С - естественного движения, при котором ядро падает на солдат противника сверху (рис. 1.1).

Рис. 1.1. Траектория движения артиллерийских снарядов
Законы полета метательных снарядов не привлекали особого внимания ученых до тех пор, пока не были изобретены дальнобойные орудия, которые посылали снаряд через холмы или деревья - так, что стреляющий не видел их полета.
Сверхдальняя стрельба из таких орудий на первых порах использовалась в основном для деморализации и устрашения противника, а точность стрельбы не играла вначале особенно важной роли.
Близко к правильному решению о полете пушечных ядер подошел итальянский математик Тарталья, он сумел показать, что наибольшей дальности полета снарядов можно достичь при направлении выстрела под углом 45° к горизонту. В его книге "Новая наука" были сформулированы правила стрельбы, которыми артиллеристы руководствовались до середины ХVII века.
Однако, полное решение проблем, связанных с движением тел брошенных горизонтально или под углом к горизонту, осуществил все тот же Галилей. В своих рассуждениях он исходил из двух основных идей: тела, движущиеся горизонтально и не подвергающиеся воздействию других сил будут сохранять свою скорость; появление внешних воздействий изменит скорость движущегося тела независимо от того, покоилось или двигалось оно до начала их действия. Галилей показал, что траектории снарядов, если пренебречь сопротивлением воздуха, представляют собой параболы.Галилей указывал, что при реальном движении снарядов, вследствие сопротивления воздуха, их траектория уже не будет напоминать параболу: нисходящая ветвь траектории будет идти несколько круче, чем расчетная кривая.
Ньютон и другие ученые разрабатывали и совершенствовали новую теорию стрельбы, с учетом возросшего влияния на движение артиллерийских снарядов сил сопротивления воздуха. Появилась и новая наука – баллистика. Прошло много-много лет, и теперь снаряды движутся столь быстро, что даже простое сравнение вида траекторий их движения подтверждает возросшее влияние сопротивления воздуха.
На рисунке 1.2 идеальная траектория движения тяжелого снаряда, вылетевшего из ствола пушки с большой начальной скоростью, показана пунктиром, а сплошной линией - действительная траектория полета снаряда при тех же условиях выстрела.

Рис. 1.2.
В современной баллистике для решения подобных задач используется электронно-вычислительная техника - компьютеры, а мы пока ограничимся простым случаем - изучением такого движения, при котором сопротивлением воздуха можно пренебречь. Это позволит нам повторить рассуждения Галилея почти без всяких изменений.
1.1.2 Движение тела, брошенного под углом к горизонту
Точное описание характера движения тела, брошенного под углом к горизонту возможно только при рассмотрении некоторой идеальной ситуации. Будем считать, что влиянием воздуха на движение можно пренебречь.
На рисунке 1.3 показана траектория движения шарика, брошенного под некоторым углом к горизонту. Траекторией движения называется кривая, отображающая положение тела в любой момент движения этого тела в выбранной системе координат. Как покажет дальнейший анализ, это знакомая из алгебры кривая, называемая параболой.
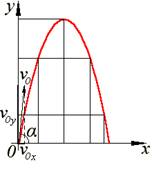
Рис. 1.3. Траектория тела, брошенного под углом а к горизонту
Если пренебречь влиянием воздуха на тело, то на тело, брошенное под углом к горизонту, как и на тело, свободно падающее, или на тело, получившую начальную скорость, направленную вертикально, действует только сила тяжести. Как бы тело не двигалось, сила тяжести может сообщить ему только ускорение g, направленное вниз. Этим и определяются и траектория движения тела, и характер его движения.
Пусть из некоторой точки O брошено тело с начальной скоростью v0, направленной под углом α к горизонту. Примем за начало отсчета координат точку, из которой брошено тело. Ось X направим горизонтально, а ось Y – вертикально вверх. Из рисунка видно, что проекции вектора v0 на оси X и Y соответственно равны v0cosα и v0sinα:
![]()
![]()
Так как на тело действует только сила тяжести, то при движении тела будет изменяться только проекция скорости v0y. Проекция же v0x изменяться не будет так же, как при прямолинейном равномерном движении:
![]() (1)
(1)
Координата же y изменяется так же, как при прямолинейном равномерном движении:
![]() (2)
(2)
Чтобы найти траекторию движения тела, надо подставить в уравнения последовательно увеличивающиеся значения t и вычислить координаты x и y и для каждого значения t при известных значениях модуля начальной скорости v0 и угла α. По полученным данным значениям x и y нанести точки, изображающие последовательное положение тела. Соединив их плавной кривой, мы и получим траекторию движения тела. Она окажется подобной той, что изображена на рисунке 1.1. Уравнение траектории можно очень просто получить из выражений (1) и (2). Подставив выражение для времени, полученное из выражения (1) в выражение (2), легко получаем уравнение траектории движения шарика, которая оказывается параболической:
![]()
2. Рабочий проект
2.1 Общие сведения о работе программе (на чем написано, какие технологии использованы)
Программа написана на языке высокого уровня Visual Basic.
При разработке были использованы следующие технологии:
· работа с массивами данных;
· работа с таблицей DataGridView;
· работа с библиотекой ZedGraph.dll и компонентом ZedGrarh, используемого для вывода графиков на экран;
· работа с компонентом MenuStrip, используемого для создания меню программы.
2.2 Основные процедуры/классы системы
В программе используются следующие основные процедуры:
1. Вычисление координат X и Y в момент времени t и заполнение списка координат list1 данными:
Dim t As New Integer
Dim Vx, Vy, x, y, g, rad, b, a1 As Double
g = 9.80665
Vx = 0, Vy = 0
x = 0, y = 0
rad = Math.PI / 180
Dim list1 As New ZedGraph.PointPairList
Dim ex As New Boolean
ex = False
t = 0
While ex = False
Vx = V * Math.Cos(a * rad)
x = Vx * t
Vy = V * Math.Sin(a * rad)
y = Vy * t - g * t * t / 2
If y < 0 Then
Dim x1, x2, y1, y2 As Double
x2 = x
y2 = y
x1 = Vx * (t - 1)
y1 = Vy * (t-1) - g * (t-1) * (t-1) / 2
a1 = (x2 - x1) / (y2 - y1)
b = y1 - a1 * x1
x = -b / a1
y = 0
ex = True
End If
list1.Add(x, y)
t = t + 1
End While
CreateGraph(zg1, list1)
zg1.Refresh()
2. Вывод графика на экран
Private Sub CreateGraph(
ByVal zg As ZedGraph.ZedGraphControl,
ByVal list1 As ZedGraph.PointPairList)
Dim myPane As ZedGraph.GraphPane
myPane = zg1.GraphPane
myPane.Title.Text = "Движение тела, брошенного
под углом к горизонту"
myPane.XAxis.Title.Text = "X(м)"
myPane.YAxis.Title.Text = "Y(м)"
myPane.CurveList.Clear()
myPane.AddCurve("График функции", list1,
Color.DarkGray, ZedGraph.SymbolType.VDash)
myPane.Chart.Fill = New ZedGraph.Fill(
Color.WhiteSmoke, Color.Azure, 45.0F)
myPane.Fill = New ZedGraph.Fill(Color.White,
Color.FromArgb(220, 220, 255), 45.0F)
zg1.AxisChange()
End Sub
Создание новых классов для реализации в программе методов движения тела, брошенного под углом к горизонту, не потребовалось.
2.3 Инсталляция программного продукта
Программа не требует предварительной установки. Необходимо лишь скопировать исполняемый файл «Движение тела, брошенного под углом к горизонту.exe» в папку «Program files» и запустить его двойным нажатием мыши на значке приложения.. При этом гарантируется полноценная работа данного приложением, даже если оно запущено не от имени администратора ПК.
При выдачи сообщения (рис. 2.1) об необходимо установить на компьютер microsoft.net framework 3.0. Для этого необходимо запустить файл «dotnetfx.exe» с диска и далее следовать указаниям инсталлятора.
Рис. 2.1. Сообщение об ошибке
2.4 Руководство пользователя
Тут вы пишете как пользоваться вашей программой. В общем виде должно быть написано следующее. Запустили экзешник удивили форму(рис. Х1). На форме есть такие то такие то поля и нужны они для того то. Далее идет скриншот формы. После этого мы заполняем поля значениями и жмем кнопку. После этого на форме появляется решение (рис. Х2). Скриншот формы с решением. После этого мы выбиравем пункт меню такой то, видим то то (рис Х3). Далее выбираем пункт выход и программа завершает свою работу
После запуска программы «Движение тела, брошенного под углом к горизонту.exe» в папку «Program files» вниманию пользователя предоставляется удобное и понятное в использовании окно программы (рис. 2.2).
В указанном окне есть поля «Начальная скорость» и «Угол к горизонту», предназначенные для задания основных параметров программы. Необходимо указать соответствующие параметры брошенного к горизонту тела. Программа автоматически выполнит необходимые вычисления и выведет график на экран. В таблице в правой части экрана выводятся значения высоты, угла движения к горизонту, времени полета при изменении дальности полета по оси X на 1 м (рис. 2.3).
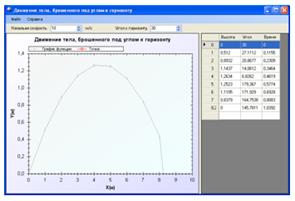
Рис. 2.2. Главное окно программы
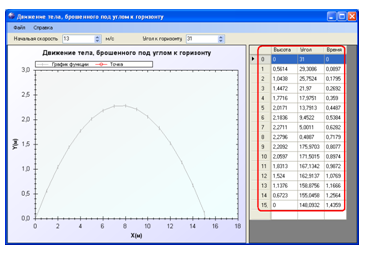
Рис. 2.3. Вывод в таблицу промежуточных значений
При выделении любой строки в таблице, соответствующая точка подсветится красным цветом (рис. 2.4).
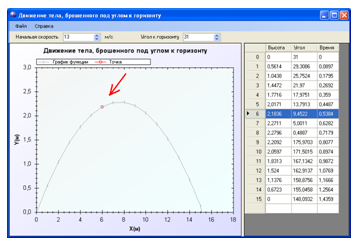
Рис. 2.4. Выделение точки на графике
2.5 Сообщения системы
При первом запуске программа может выдать ошибку, представленную на рисунке 2.1. Порядок ее устранения описан в п. 2.3.
Никаких других сообщений система не выдает, диапазоны вводимых данных контролируются автоматически.
2.6 Требования к техническому и программному обеспечению
Разрабатываемая программа должна соответствовать следующим минимальным требованиям, обусловленным заданием к проекту.
2.6.1 Требования к программному обеспечению
· ОС — Windows NT/2000/XP/2003/Vista;
· Microsoft.net framework 3.0.
2.6.2 Требования к техническому обеспечению
· IBM-совместимый компьютер с МП Intel Pentium III или AMD K6 с тактовой частотой 500 МГц и выше;
· 64 MB ОЗУ;
· НЖМД со свободным пространством 1 МБ;
· Клавиатура;
· Мышь.
2.7 Тестирование системы
Программа тестировалась на предмет наличия ошибок. На бумаге были рассчитаны эталонные значения высоты, угла и времени полета тела, брошенного под углов к горизонту, при заданных параметрах V0=10 и a=30. Полученные результаты представлены в таблице 2.1.
Таблица 2.1.Эталонные значения
| Длина полета (м) | Высота полета (м) | Угол наклона к горизонту | Время полета (с) |
| 0 | 0 | 30 | 0 |
| 1 | 0,512 | 27,1112 | 0,1155 |
| 2 | 0,8932 | 20,8677 | 0,2309 |
| 3 | 1,1437 | 14,0612 | 0,3464 |
| 4 | 1,2634 | 6,8262 | 0,4619 |
| 5 | 1,2523 | 179,367 | 0,5774 |
| 6 | 1,1105 | 171,929 | 0,6928 |
| 7 | 0,8379 | 164,7538 | 0,8083 |
| 8 | 0,4346 | 158,0351 | 0,9238 |
Программа показала идентичные результаты.
Заключение
Курсовой проект выполнен в среде MS Visual Studio 2008 с использованием языка высокого уровня Visual Basic.
Разработка проекта проходила в несколько стадий, заключавшихся в изучении предметной области задачи; изучении основных законов механики; разработке самой программы, позволяющей моделировать движение тела, брошенного под углом к горизонту.
Результатом проделанной работы стала программа, реализующая модель движения тела, брошенного под углом к горизонту. Программный продукт был протестирован в системах MS Windows XP, MS Windows 2003. В процессе тестирования ошибок выявлено не было. Практическая ценность программы была доказана при сопоставлении скорости выполнения расчетов вручную и с использованием разработанной программы.
В течение разработки курсовой работы закреплены практические навыки программирования, полученные на лабораторных занятиях по дисциплине "Высокоуровневые методы информатики и программирования", углублены теоретические и практические знаний в области методологии программирования и разработки программных комплексов.
Так же курсовая работа поспособствовала развитию навыков самостоятельного планирования и выполнения научно-исследовательской работы, получению опыта сбора и обработки исходного материала, анализа научно-технической литературы, справочников, стандартов и технической документации, приобретению навыков обоснования принимаемых проектных решений и профессионального оформления проектной документации.
Список литературы
1.В.В. Лабор «Visual Basic: создание приложений для Windows. Практическое пособие для новичков и профессионалов» Минск, «Харвест», 2003 г.
2.Ч. Петцольд «Программирование для Microsoft Windows на Basic, Пер. с англ. – М,: издательско-торговый дом «Русская Редакция», 2002 г.
3.Алешкевич В.А. Деденко Л.Г. Караваев В.А., «Механика», Академия 2004.
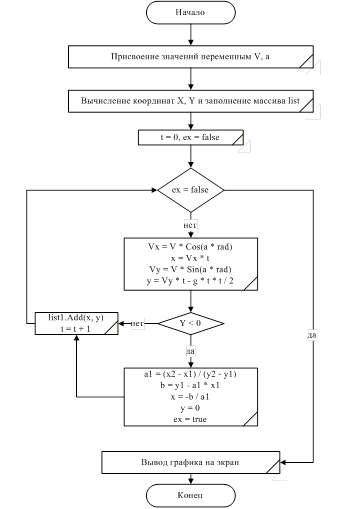
Приложение 1
Блок-схема
| Вычислительная математика | |
|
Содержание Введение Тема 1. Решение задач вычислительными методами. Основные понятия 1.1 Погрешность 1.2 Корректность 1.3 Вычислительные методы Тема 2 ... 2.3 - 2.6 показаны четыре случая взаимного расположения линий y = x и y = j(x) и соответствующие итерационные процессы. Производную y'(t) в каждой точке (t, y) можно геометрически интерпретировать как тангенс угла a наклона касательной к графику решения, проходящего через эту точку, т е.: k = tga ... |
Раздел: Рефераты по математике Тип: учебное пособие |
| Оборудование летательных аппаратов | |
|
Практическая работа N12-6 СИСТЕМА ВОЗДУШНЫХ СИГНАЛОВ СВС-72-3 (Продолжительность практической работы - 4 часа) I. ЦЕЛЬ РАБОТЫ Целью работы ячвляется ... Величина ухода ?=???t в плоскости горизонта, обусловленная вертикальной составляющей ?зв угловой скорости вращения Земли, является погрешностью ГПК в измерении курса. Уход же ГПК в плоскости горизонта ("в азимуте") из-за движения ЛА зависит от вида траектории. |
Раздел: Рефераты по авиации и космонавтике Тип: реферат |
| ... подготовки обработки детали станка с числовым программным управлением | |
|
... мехатронной системы станка с ЧПУ 1.1 Общая структура и классификация систем ЧПУ 1.2 Обоснование применения программного управления оборудованием 1.3 ... Использование данного программного модуля должно обеспечить корректное преобразование траектории движения инструмента и технологические команды в коды управления соответствующей ... Системы ЧПУ, обеспечивающие прямолинейное (под любым углом к координатным осям станка) формообразование и позиционирование, управляют движением инструмента при резании одновременно ... |
Раздел: Промышленность, производство Тип: дипломная работа |
| Математическая модель системы слежения РЛС | |
|
Содержание Содержание. 1 Введение. 3 1 Общая теория оптимального управления. 6 1.1 Допустимые управления. 6 1.2 Основные направления в теории ... Задача оптимального быстродействия заключается в отыскании такого управления u(t), для которого фазовая траектория x(t) проходит через точку x1 и переход из х0 в х1 осуществляется ... На рисунке 2.5 представлены усредненные траектории, а на рисунке 2.6. - интерполированные; рисунки а) представляют собой угол поворота, а рисунки б) - скорость. |
Раздел: Рефераты по математике Тип: дипломная работа |
| Разработка алгоритмов контроля и диагностики системы управления ... | |
|
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ "ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ" Факультет І Кафедра "Системи та процеси ... Имея непрерывно измеряемые значения p(t), q(t), r(t), вычислительная машина интегрирует кинематические уравнения углового движения и непрерывно определяет соответствующие три угла ... Поскольку скорость полета определяется законами небесной механики, постольку при изменении высоты полета на малую долю радиуса планеты скорость изменяется мало. |
Раздел: Рефераты по авиации и космонавтике Тип: реферат |