Реферат: Інтегральні характеристики векторних полів

інтегральні характеристики векторних полів

1. Диференціальні операції другого порядку

Нехай в області  задані скалярне поле  і векторне поле , причому функції  мають в області  неперервні частинні похідні другого порядку. Тоді  і  є диференційовними векторними полями, а  – диференційовним скалярним полем.

До векторних полів  і  можна застосувати операції обчислення дивергенції і ротора, а до скалярного поля  – операцію обчислення градієнта. Таким чином, отримуємо повторні операції:

.

Операцію  називають оператором Лапласа і позначають також символом :

.

З допомогою оператора Гамільтона оператор Лапласа записується у вигляді

.

Враховуючи, що

,

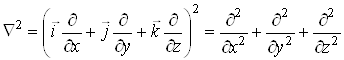дістаємо

.

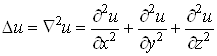Функція , яка задовольняє в деякій області рівняння Лапласа , називається гармонічною в цій області. Наприклад, лінійна функція  є гармонічною в довільній області. Оператор Лапласа широко застосовується в рівняннях математичної фізики. Відзначимо, зокрема, що потенціал електричного поля точкового заряду або поля тяжіння точкової маси, який має вигляд , при  задовольняє рівняння Лапласа:

(потенціальне векторне поле  є безвихровим) і

(векторне поле  є соленоїдальним).

1. Дві інші повторні операції  і  пов’язані співвідношенням

,                                             (1)

де – вектор-функція, координатами якої є результати застосування оператора Лапласа до функцій .

2. Розкладання векторного поля на суму потенціального і соленоїдального полів

Довільне неперервно диференційовне векторне поле  може бути зображено у вигляді

,                                              (2)

де  – потенціальне поле,  – соленоїдальне поле.

Дійсно, за означенням потенціальне векторне поле  є градієнтом деякого скалярного поля : . Тому для вектора  із рівності (2) маємо

.                                       (3)

Щоб векторне поле  було соленоїдальним, воно має задовольняти умову , звідси, враховуючи рівність (3), знаходимо

.

Таким чином, для скалярного потенціала поля  отримуємо рівняння

,                                                 (4)

де  – відома функція даного поля .

Отже, якщо функція  є розв’язком рівняння (4), то, поклавши , , отримаємо зображення поля  у вигляді (2), де  – потенціальне поле,  – соленоїдальне поле.

Рівняння (2) – неоднорідне рівняння в частинних похідних другого порядку, яке називається рівнянням Пуассона:

.

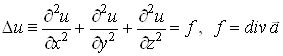Відзначимо, що це рівняння має (нескінченну) множину розв’язків, тому зображення поля  у вигляді (2) не є єдиним.

2. Потік векторного поля

Розглянемо векторне поле , визначене в просторовій області , і деяку кусково-гладку орієнтовну поверхню . Нехай  – поле одиничних нормалей на обраній стороні поверхні .

Як було відзначено в п. 4.2, поверхневий інтеграл

                                             (5)

називається потоком векторного поля  через поверхню  в сторону, яка визначається вектором  (кажуть також «потік через обрану сторону поверхні »).

Якщо взяти іншу сторону поверхні (змінити орієнтацію), то вектор  змінить напрям на протилежний; тому скалярний добуток , а отже, і потік (поверхневий інтеграл (5)) змінить знак.

Якщо  – швидкість рухомої рідини, то  є кількістю (об’ємом) рідини, яка протікає через поверхню  у напрямі нормалі  за одиницю часу. Ця величина називається у фізиці (гідродинаміці) потоком рідини через поверхню . Тому і у випадку довільного векторного поля  інтеграл (5) називається потоком векторного поля через поверхню .

Розглянемо електричне поле  точкового заряду , який міститься в точці . Знайдемо потік векторного поля  через зовнішню сторону сфери  радіуса  з центром у точці . Нехай  ( – точка на сфері ); тоді . Тому

,

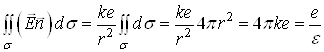де  – діелектрична проникність середовища, .

Якщо в системі координат  , а , то вираз (5) для потоку векторного поля  можна записати у вигляді

.          (6)

Кожен доданок у правій частині рівності (6) залежить від вибору системи координат, проте їх сума, тобто потік , очевидно, не залежить від вибору системи координат.

3. Формула Остроградського-Гаусса в векторній формі

Нехай в області  визначено векторне поле ;  – замкнена поверхня, яка обмежує область ;  – одиничний вектор зовнішньої нормалі до поверхні  у точці .

Нехай, далі,  та їхні частинні похідні 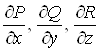 неперервні в області . Тоді справедлива формула Остроградського-Гаусса:

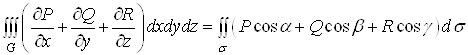.         (7)

Підінтегральна функція в потрійному інтегралі є , а поверхневий інтеграл – потік векторного поля  через поверхню . Тому формулу (7) можна записати у векторній формі:

.                                        (8)

Фізичний зміст формули Остроградського-Гаусса: потік векторного поля  через замкнену поверхню в сторону зовнішньої нормалі дорівнює потрійному інтегралу по області, обмеженій цією поверхнею, від дивергенції векторного поля . Щоб потік був відмінним від нуля, всередині області  мають бути джерела (або стоки) поля. Із формули Остроградського-Гаусса випливає, що тоді  є відмінною від нуля. Таким чином,  характеризує джерела поля. Само векторне поле як би розходиться від джерел. Звідси і походить назва «розбіжність» або «дивергенція».

4. Властивості соленоїдального поля

Як відомо, векторне поле , яке задовольняє в області  умову , називається соленоїдальним в цій області. Нехай область  є об’ємно однозв’язною. Це означає, що, якщо кусково-гладка замкнена поверхня  лежить в області , то і область, яка обмежує поверхню , цілком належить області . Прикладами об’ємно однозв’язних областей є куля, паралелепіпед, тор. Відзначимо, що тор не є поверхнево однозв’язною областю. Область, яка знаходиться між двома сферами, не є об’ємно однозв’язною (але є поверхнево однозв’язною).

Із формули Остроградського-Гаусса випливає, що соленоїдальне поле в взаємно однозв’язній області має таку властивість: потік соленоїдального поля через довільну замкнену поверхню, яка знаходиться в цій області, дорівнює нулю.

Відзначимо, що, якщо область не є об’ємно однозв’язною, то потік соленоїдального (в цій області) поля через замкнену поверхню, яка знаходиться в області, може бути відмінним від нуля. Так електричне поле  точкового заряду, який міститься в точці , є соленоїдальним в кулі з викинутим центром ( при ).

Слово «соленоїдальне» означає «трубасте». Для соленоїдального поля є справедливим закон збереження інтенсивності векторної трубки. З’ясуємо суть цього закону.

Нехай  – соленоїдальне поле. Розглянемо відрізок «векторної трубки», тобто область, обмежену двома перерізами  і  та боковою поверхнею , яка складається із векторних ліній (рис. 1). Застосуємо до такої області формулу Остроградського-Гаусса (8). Оскільки в соленоїдальному полі , то потік векторного поля  через поверхню області дорівнює нулю:  ( – одиничний вектор зовнішньої нормалі). На боковій поверхні  маємо , тому .

Отже,

.

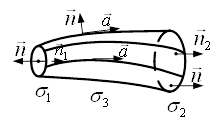
Рисунок 1 – Відрізок «векторної трубки»

Змінимо на перерізі  напрям нормалі  на протилежний ( – внутрішня нормаль до ). Тоді отримаємо

,

де обидва потоки через перерізи  і  обчислюються в напрямі векторних ліній.

Таким чином, у соленоїдальному (трубчастому) векторному полі  потік через будь-який переріз векторної трубки набуває одного й того самого значення. Це і є закон збереження інтенсивності збереження векторної трубки.

5. Інваріантне означення дивергенції

Нехай в області , обмеженій поверхнею , визначено векторне поле . Запишемо формулу (8) для векторного поля  в області . Застосовуючи до лівої частини цієї формули теорему про середнє, отримаємо

або

,

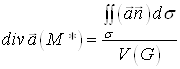де  – об’єм області , а  – деяка точка області .

Зафіксуємо точку  і стягуватимемо область  до точки  так, щоб  залишалася внутрішньою точкою області . Тоді , а  прямуватиме до . Внаслідок неперервності  значення  прямуватиме до . Таким чином, отримуємо

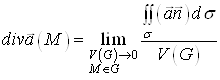.                                        (9)

У праву частину формули (9) входять величини, інваріантні відносно вибору системи координат (потік векторного поля через поверхню і об’єм області). Тому формула (9) дає інваріантне означення дивергенції векторного поля. Отже, дивергенція векторного поля залежить тільки від самого поля і не залежить від вибору системи координат.

6. Циркуляція векторного поля

Розглянемо векторне поле , визначене в просторовій області , і деяку кусково-гладку криву , на якій вказано напрям обходу (вибір напряму обходу називають також орієнтацією кривої). Нехай  – одиничний дотичний вектор до кривої  у точці , напрямлений в сторону обходу кривої.

Криволінійний інтеграл

                                        (10)

називається циркуляцією векторного поля  вздовж кривої  у заданому напрямі.

Якщо взяти інший напрям обходу кривої (змінити орієнтацію), то вектор  змінить напрям на протилежний, тому скалярний добуток , а, отже, і циркуляція (криволінійний інтеграл (10)) змінить знак.

Якщо  – силове векторне поле, тобто  – вектор сили, то циркуляція  визначає роботу силового векторного поля вздовж кривої  в заданому напрямі.

Якщо в прямокутній системі координат  , а , то вираз (10) для циркуляції векторного поля  можна записати в вигляді

.              (11)

Кожний доданок у правій частині (11) залежить від вибору системи координат, проте їхня сума, тобто циркуляція , очевидно, не залежить від вибору системи координат.

Якщо ввести вектор , то циркуляцію можна записати у вигляді  (порівняйте з правою частиною рівності (11)).

7. Формула Стокса у векторній формі

Нехай в області  визначено векторне поле ;  – замкнений контур, який лежить в області ;  – довільна поверхня, межею якої є контур ;  («поверхня  натягнута на контур »);  – одиничний вектор нормалі на обраній стороні поверхні .

Нехай функції  та їхні частинні похідні першого порядку неперервні на поверхні . Тоді справедлива формула Стокса

,

де орієнтація контуру  узгоджена з орієнтацією поверхні . Ліва частина формули Стокса є циркуляцією векторного поля  вздовж контура , а права частина визначає потік через поверхню  векторного поля з координатами 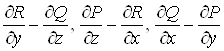, тобто потік  через поверхню . Тому формулу Стокса можна записати у векторній формі:

                                    (12)

або

.                                     (13)

Фізичний зміст формули Стокса: циркуляція векторного поля  вздовж замкненого контуру дорівнює потоку ротора векторного поля  через поверхню, натягнуту на цей контур.

8. Властивості потенціального поля

Як відомо, векторне поле , яке задовольняє в області  умову , називається потенціальним у цій області ( – скалярний потенціал поля ). Якщо поле  потенціальне в області , то 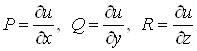 і вираз 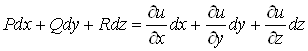 є повним диференціалом функції  в області . Це означає, що виконана умова незалежності криволінійного інтеграла від шляху інтегрування в просторі.

Таким чином, потенціальне в області  поле має такі властивості.

1. Циркуляція потенціального поля  вздовж довільного замкненого контуру  дорівнює нулю:

.

2. Для довільних точок  і  області  циркуляція потенціального поля  вздовж кривої  не залежить від вибору кривої  і дорівнює різниці значень потенціала  в точках  і :

.

У випадку силового потенціального поля ця властивість означає, що робота такого поля вздовж кривої  не залежить від вибору кривої, а залежить тільки від початкової і кінцевої точок  і .

3. Потенціальне поле  є безвихровим, тобто .

Нехай тепер дано векторне поле , яке задовольняє в області  умову . Чи випливає звідси, що поле  є потенціальним в області ? Відповідь на це запитання залежить від форми області . Якщо область  є поверхнево однозв’язною, то із умови  випливає, що існує функція  така, що

.

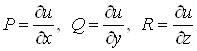Отже, 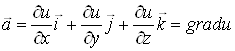, тобто поле  є потенціальним в області .

Таким чином, умова  є необхідною і достатньою умовою потенціальності поля  у поверхнево однозв’язній області.

Потенціал  потенціального поля  у поверхнево однозв’язній області можна обчислити за формулою:

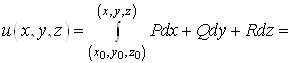
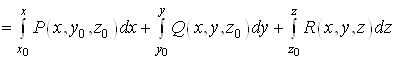.              (14)

Якщо область  не є поверхнево однозв’язною, то умова  не є достатньою для потенціальності поля  в області .

9. Інваріантне означення ротора

Нехай в області  визначено векторне поле . Зафіксуємо точку  і деяку площину, яка проходить через цю точку. Нехай  – одиничний вектор нормалі до площини,  – замкнений контур, який лежить в площині і обмежує область  таку, що  – внутрішня точка області . Запишемо формулу (12) для векторного поля  в області . Застосовуючи до правої частини цієї формули теорему про середнє, отримуємо

,

диференціальне векторне поле формула соленоїдальне

звідки

,

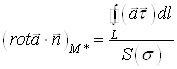де  – площа області ,  – деяка точка області .

Стягуватимемо область  до точки  так, щоб  залишалася внутрішньою точкою області . Тоді , а  прямуватимемо до . Внаслідок неперервності  значення  прямуватимемо до . Таким чином, отримуємо

.

У праву частину формули входять величини, інваріантні відносно вибору системи координат (циркуляція векторного поля вздовж замкненого контура і площа плоскої області). Тому дана формула дає інваріантне означення проекції  в точці  на напрям, який виражається заданим вектором .

Отже, проекція ротора векторного поля на довільний напрям, а отже, і сам  залежить тільки від векторного поля  і не залежить від вибору системи координат.

Для означення вектора  вищезазначеним способом достатньо розглянути в заданій точці  проекції  на три довільних некомпланарних напрями. Такими трьома проекціями  визначається однозначно.

Размещено на http://www.