Контрольная работа: Подвійний інтеграл
ПОДВІЙНИЙ ІНТЕГРАЛ
Содержание
1. Задачі, що приводять до поняття подвійного інтеграла
Задача про об'єм циліндричного тіла
Задача про масу пластини
2. Поняття подвійного інтеграла. Умови його існування та властивості
3. Обчислення подвійного інтеграла
1. Задачі, що приводять до поняття подвійного інтеграла Задача про об'єм циліндричного тіла
Нехай маємо тіло, обмежене
зверху поверхнею ![]() , знизу - замкненою обмеженою областю
, знизу - замкненою обмеженою областю
![]() площини
площини ![]() , з боків - циліндричною поверхнею, напрямна якої збігається з межею
області
, з боків - циліндричною поверхнею, напрямна якої збігається з межею
області ![]() , а
твірні паралельні осі
, а
твірні паралельні осі ![]() (рис.1). Таке тіло називають циліндричним.
(рис.1). Таке тіло називають циліндричним.
Обчислимо його об'єм ![]() .
Для цього довільним способом розіб'ємо область
.
Для цього довільним способом розіб'ємо область ![]() на
на ![]() частин
частин ![]() , які не мають спільних внутрішніх
точок, і площі яких дорівнюють
, які не мають спільних внутрішніх
точок, і площі яких дорівнюють ![]() ,
, ![]() . У кожній області
. У кожній області
![]() виберемо довільну
точку
виберемо довільну
точку ![]() , знайдемо
значення функції в цій точці
, знайдемо
значення функції в цій точці ![]() і обчислимо добуток
і обчислимо добуток ![]()
![]() . Цей добуток дорівнює об'єму
циліндричного стовпчика з твірними, паралельними осі
. Цей добуток дорівнює об'єму
циліндричного стовпчика з твірними, паралельними осі ![]() , основою
, основою ![]() і висотою
і висотою ![]() . Усього таких
стовпчиків є
. Усього таких
стовпчиків є ![]() , і сума їхніх об'ємів
, і сума їхніх об'ємів
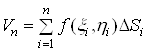 (1)
(1)
наближено дорівнює об'єму
циліндричного тіла ![]() . Це наближення тим точніше, чим більше
число
. Це наближення тим точніше, чим більше
число ![]() і чим
менші розміри областей
і чим
менші розміри областей ![]() . Назвемо діаметром
. Назвемо діаметром ![]() замкненої обмеженої області
замкненої обмеженої області
![]() найбільшу
відстань між двома точками межі цієї області. Позначимо через
найбільшу
відстань між двома точками межі цієї області. Позначимо через ![]() найбільший з діаметрів областей
найбільший з діаметрів областей
![]() . Тоді природно
об'єм даного тіла визначити як границю суми (1) при
. Тоді природно
об'єм даного тіла визначити як границю суми (1) при ![]() :
:
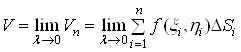 . (2)
. (2)
Нехай маємо плоску неоднорідну
матеріальну пластину, формою якої є область ![]() (рис.2). В області
(рис.2). В області ![]() задана неперервна функція
задана неперервна функція ![]() , яка визначає густину
пластини в точці
, яка визначає густину
пластини в точці ![]() . Знайдемо масу
. Знайдемо масу
![]() пластини. Для цього довільним способом розіб'ємо область
пластини. Для цього довільним способом розіб'ємо область ![]() на частини
на частини ![]() , які не мають спільних
внутрішніх точок, і площі яких дорівнюють
, які не мають спільних
внутрішніх точок, і площі яких дорівнюють ![]() ,
, ![]() .
.
У кожній області ![]() візьмемо будь-яку
точку
візьмемо будь-яку
точку ![]() і знайдемо
густину в цій точці:
і знайдемо
густину в цій точці:
![]() .
.
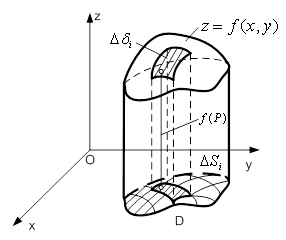
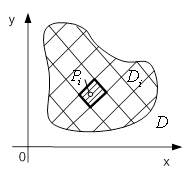
Рисунок 1 - Циліндричне тіло Рисунок 2 - Матеріальна пластина
Якщо розміри області ![]() достатньо малі,
то густина в кожній точці
достатньо малі,
то густина в кожній точці ![]() мало відрізнятиметься від значення
мало відрізнятиметься від значення
![]() . Тоді добуток
. Тоді добуток
![]()
![]() наближено визначає
масу тієї частини пластини, яка займає область
наближено визначає
масу тієї частини пластини, яка займає область ![]() , а сума
, а сума
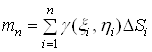 (3)
(3)
є наближеним значенням
маси ![]() всієї
пластини. Точне значення маси отримаємо як границю суми (3) при
всієї
пластини. Точне значення маси отримаємо як границю суми (3) при ![]() :
:
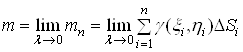 . (4)
. (4)
Таким чином, різні за змістом задачі ми звели до знаходження границь (2) і (4) одного й того самого виду. Можна навести ще ряд задач з фізики і техніки, розв'язання яких призводить до обчислення подібних границь. У зв'язку з цим виникає потреба у вивченні властивостей цих границь, незалежно від змісту тієї чи іншої задачі. Кожна така границя називається подвійним інтегралом. Дамо точні означення.
2. Поняття подвійного інтеграла. Умови його існування та властивості
Нехай функція ![]() визначена
в замкненій обмеженій області
визначена
в замкненій обмеженій області ![]() . Вважатимемо, що межа області
. Вважатимемо, що межа області ![]() складається із
скінченного числа неперервних кривих, кожна з яких визначається функцією виду
складається із
скінченного числа неперервних кривих, кожна з яких визначається функцією виду ![]() або
або ![]() .
Розіб'ємо область
.
Розіб'ємо область ![]() на
на ![]() частини
частини ![]() , які не мають спільних внутрішніх точок і площі яких дорівнюють
, які не мають спільних внутрішніх точок і площі яких дорівнюють
![]() ,
, ![]() .
У кожній області
.
У кожній області ![]() візьмемо довільну
точку
візьмемо довільну
точку ![]() і утворимо
суму
і утворимо
суму
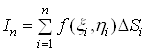 , (5)
, (5)
яку назвемо інтегральною сумою для функції![]() за областю
за областю
![]() . Нехай
. Нехай ![]() - найбільший з діаметрів областей
- найбільший з діаметрів областей
![]() . Якщо інтегральна сума (5) при
. Якщо інтегральна сума (5) при ![]() має скінченну границю, яка не залежить
ні від способу розбиття області
має скінченну границю, яка не залежить
ні від способу розбиття області ![]() на частинні області
на частинні області ![]() , ні від вибору
точок
, ні від вибору
точок ![]() в них,
то ця границя називається подвійним інтегралом і позначається
одним із таких символів:
в них,
то ця границя називається подвійним інтегралом і позначається
одним із таких символів:
![]() або
або ![]() .
.
Таким чином, за означенням
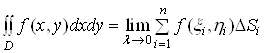 . (6)
. (6)
У цьому випадку функція
![]() називається
інтегровною в області
називається
інтегровною в області![]() ;
;
![]() - областю
інтегрування;
- областю
інтегрування; ![]() - змінними інтегрування;
- змінними інтегрування;
![]() (або
(або
![]() ) - елементом площі.
) - елементом площі.
Звернемося до задач п. Якщо границі в рівностях (2) і (4) існують, то з цих рівностей і формули (6) отримуємо формули для обчислення об'єму циліндричного тіла
![]() (7)
(7)
та маси пластинки
![]() . (8)
. (8)
Якщо у формулі (7) покласти
![]() ,
, ![]() , то отримаємо формулу
для обчислення площі
, то отримаємо формулу
для обчислення площі ![]() області
області ![]() :
:
![]() . (9)
. (9)
Рівності (7) і (8) розглядають
відповідно як геометричний та механічний зміст подвійного інтеграла, якщо підінтегральна
функція невід'ємна в області![]() .
.
Теорема (достатня умова інтегровності функції). Якщо функція ![]() неперервна в замкненій обмеженій області
неперервна в замкненій обмеженій області![]() , то вона інтегровна в цій області.
, то вона інтегровна в цій області.
Є ще й інші умови існування
подвійного інтеграла, але надалі ми вважатимемо, що підінтегральна функція ![]() в області інтегрування
в області інтегрування
![]() є неперервною.
є неперервною.
Порівнюючи означення подвійного інтеграла (6) та означення визначеного інтеграла
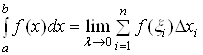 ,
,
бачимо, що конструктивно
ці означення цілком аналогічні: в обох випадках розглядається деяка функція ![]() , але в першому
випадку це функція однієї змінної, визначена на одновимірній області - відрізку
, але в першому
випадку це функція однієї змінної, визначена на одновимірній області - відрізку
![]() , а в другому
- це функція двох змінних, визначена у двовимірній області
, а в другому
- це функція двох змінних, визначена у двовимірній області![]() . В
обох випадках область визначення розбивається на частини, в кожній з яких береться
довільна точка і в ній знаходиться значення функції. Після цього знайдене значення
функції множиться на міру відповідної частини області визначення. У випадку однієї
змінної такою мірою була довжина
. В
обох випадках область визначення розбивається на частини, в кожній з яких береться
довільна точка і в ній знаходиться значення функції. Після цього знайдене значення
функції множиться на міру відповідної частини області визначення. У випадку однієї
змінної такою мірою була довжина ![]() відрізка
відрізка ![]() , а у випадку
двох змінних - площа
, а у випадку
двох змінних - площа ![]() області
області ![]() . Наступні кроки
знову однакові: утворюються інтегральні суми і знаходяться їхні границі, коли міра
частин області визначення прямує до нуля. Пізніше ми побачимо, що за цією самою
схемою будується і потрійний інтеграл, тільки мірою області там є об'єм.
. Наступні кроки
знову однакові: утворюються інтегральні суми і знаходяться їхні границі, коли міра
частин області визначення прямує до нуля. Пізніше ми побачимо, що за цією самою
схемою будується і потрійний інтеграл, тільки мірою області там є об'єм.
У зв'язку з цим, властивості подвійного інтеграла аналогічні відповідним властивостям визначеного інтеграла. Сформулюємо ці властивості.
Сталий множник можна винести за знак подвійного інтеграла:
![]() ,
, ![]() .
.
Подвійний інтеграл від суми двох функцій дорівнює сумі подвійних інтегралів від цих функцій:
![]() .
.
Ця властивість має місце для суми довільного скінченного числа функцій.
Якщо в
області ![]() функція
функція![]() , то
, то
![]() .
.
Якщо функції
![]() і
і ![]() визначені в одній і тій самій області
визначені в одній і тій самій області ![]() і
і ![]() , то
, то
![]() .
.
(Адитивність
подвійного інтеграла). Якщо область інтегрування функції ![]() розбити на області
розбити на області ![]() і
і ![]() , які не мають спільних внутрішніх точок, то
, які не мають спільних внутрішніх точок, то
![]() .
.
Ця властивість називається
адитивністю подвійного інтеграла і справедлива для довільного
скінченого числа областей, які складають область ![]() і не мають спільних внутрішніх точок.
і не мають спільних внутрішніх точок.
(Оцінка
подвійного інтеграла). Якщо функція неперервна в обмеженій замкненій області ![]() , яка має площу
, яка має площу ![]() , то
, то
![]() ,
,
де ![]() і
і ![]() - відповідно найменше і найбільше значення підінтегральної
функції в області
- відповідно найменше і найбільше значення підінтегральної
функції в області ![]() .
.
(Середнє
значення функції.) Якщо функція ![]() неперервна в замкненій
обмеженій області
неперервна в замкненій
обмеженій області ![]() , яка має площу
, яка має площу
![]() , то в цій області існує така точка
, то в цій області існує така точка ![]() що
що
![]() .
.
Величину
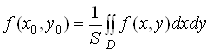
називають середнім значенням функції ![]() в області
в області
![]() .
.
подвійний інтеграл адитивність
3. Обчислення подвійного інтеграла
Обчислення подвійного інтеграла за формулою (6) як границі інтегральної суми, так само як і у випадку визначеного інтеграла, пов'язане із значними труднощами. Щоб уникнути їх, обчислення подвійного інтеграла зводять до обчислення так званого повторного інтеграла - двох звичайних визначених інтегралів.
Покажемо, як це робиться.
Припустимо, що при ![]() функція
функція ![]() . Тоді, згідно з формулою (7), подвійний
інтеграл виражає об'єм циліндричного тіла (рис.3) з основою
. Тоді, згідно з формулою (7), подвійний
інтеграл виражає об'єм циліндричного тіла (рис.3) з основою ![]() , обмеженого зверху поверхнею
, обмеженого зверху поверхнею
![]() . Обчислимо
цей об'єм за допомогою методу паралельних перерізів [6]:
. Обчислимо
цей об'єм за допомогою методу паралельних перерізів [6]:
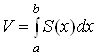 ,
,
де ![]() - площа перерізу тіла площиною,
перпендикулярною до осі
- площа перерізу тіла площиною,
перпендикулярною до осі ![]() , а
, а ![]() та
та ![]() - рівняння площин, які обмежують дане
тіло. Перед тим, як обчислювати площу зробимо певні припущення відносно області
- рівняння площин, які обмежують дане
тіло. Перед тим, як обчислювати площу зробимо певні припущення відносно області
![]() .
.
Припустимо спочатку, що
область інтегрування ![]() обмежена двома неперервними кривими
обмежена двома неперервними кривими
![]() та
та ![]() і двома прямими
і двома прямими
![]() та
та ![]() , причому
, причому ![]() для всіх
для всіх ![]() (рис.4). Проведемо
через точку
(рис.4). Проведемо
через точку ![]() ,
де
,
де ![]() , пряму, паралельну осі
, пряму, паралельну осі ![]() . Ця пряма перетинає
криві
. Ця пряма перетинає
криві ![]() та
та ![]() в
точках
в
точках ![]() і
і ![]() , які називатимемо відповідно точкою
входу в область
, які називатимемо відповідно точкою
входу в область ![]() і точкою виходу
з області
і точкою виходу
з області ![]() .
Ординати цих точок позначимо відповідно
.
Ординати цих точок позначимо відповідно ![]() та
та ![]() , тоді
, тоді ![]() ,
, ![]() .
.
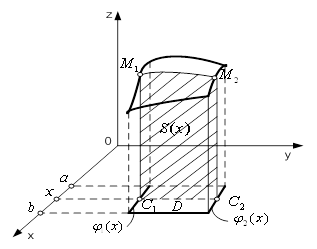
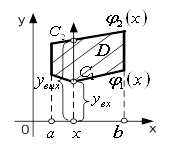
Рисунок 3 - Циліндричне
тіло Рисунок 4 - Область ![]()
Визначена таким чином
область називається правильною в напрямі осі ![]() . Інакше кажучи, область
. Інакше кажучи, область ![]() називається правильною в напрямі осі
називається правильною в напрямі осі
![]() , якщо довільна пряма, яка проходить через внутрішню точку області
, якщо довільна пряма, яка проходить через внутрішню точку області
![]() паралельно осі
паралельно осі ![]() , перетинає межу
області не більше, ніж у двох точках.
, перетинає межу
області не більше, ніж у двох точках.
Знайдемо тепер площу ![]() .
Для цього проведемо через точку
.
Для цього проведемо через точку ![]() площину, перпендикулярну осі
площину, перпендикулярну осі ![]() (рис.3).
У перерізі цієї площини і циліндричного тіла утворюється трапеція
(рис.3).
У перерізі цієї площини і циліндричного тіла утворюється трапеція ![]() . Апліката
. Апліката ![]() точки лінії
точки лінії ![]() при
фіксованому
при
фіксованому ![]() є функцією лише
є функцією лише ![]() , причому
, причому ![]() змінюється
в межах від
змінюється
в межах від ![]() до
до
![]() . Площа
. Площа ![]() трапеції
трапеції ![]() дорівнює визначеному
інтегралу
дорівнює визначеному
інтегралу
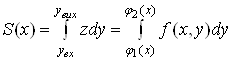 .
.
Підставивши знайдене значення
![]() у формулу
у формулу 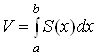 і враховуючи формулу
(7), отримаємо
і враховуючи формулу
(7), отримаємо
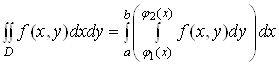
або в зручнішій формі
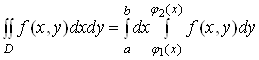 . (10)
. (10)
Це і є шукана формула
для обчислення подвійного інтеграла. Праву частину формули (10) називають повторним інтегралом від функції ![]() за областю
за областю![]() . У повторному інтегралі
(10) інтегрування виконується спочатку за змінною
. У повторному інтегралі
(10) інтегрування виконується спочатку за змінною ![]() (при цьому
(при цьому ![]() вважається
сталою), а потім за змінною
вважається
сталою), а потім за змінною ![]() . Інтеграл за
змінною
. Інтеграл за
змінною ![]() називають внутрішнім, а за змінною
називають внутрішнім, а за змінною ![]() - зовнішнім. У результаті обчислення
внутрішнього інтеграла (в межах від
- зовнішнім. У результаті обчислення
внутрішнього інтеграла (в межах від ![]() до
до ![]() ) одержуємо певну функцію від однієї
змінної
) одержуємо певну функцію від однієї
змінної ![]() . Інтегруючи цю функцію в межах від
. Інтегруючи цю функцію в межах від ![]() до
до ![]() ,
тобто обчислюючи зовнішній інтеграл, отримаємо деяке число - значення подвійного
інтеграла. Зауваження Наведені геометричні міркування при
одержанні формули (10) можливі у випадку, коли
,
тобто обчислюючи зовнішній інтеграл, отримаємо деяке число - значення подвійного
інтеграла. Зауваження Наведені геометричні міркування при
одержанні формули (10) можливі у випадку, коли ![]() . Проте формула (10) залишається справедливою
і в загальному випадку. Зауваження 2. Якщо область
. Проте формула (10) залишається справедливою
і в загальному випадку. Зауваження 2. Якщо область ![]() обмежена
двома неперервними кривими
обмежена
двома неперервними кривими ![]() і двома прямими
і двома прямими ![]() причому
причому ![]() для всіх
для всіх ![]() , тобто якщо область
, тобто якщо область ![]() правильна в напрямі осі
правильна в напрямі осі ![]() (рис.5),
то справедлива формула
(рис.5),
то справедлива формула
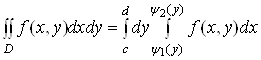 . (11)
. (11)
Тут внутрішнім є інтеграл
за змінною ![]() . Обчислюючи його в межах від
. Обчислюючи його в межах від ![]() до
до ![]() (при цьому
(при цьому ![]() вважається
сталою), отримаємо деяку функцію від однієї змінної
вважається
сталою), отримаємо деяку функцію від однієї змінної ![]() . Інтегруючи
потім цю функцію в межах від
. Інтегруючи
потім цю функцію в межах від ![]() до
до ![]() , отримаємо значення
подвійного інтеграла.
, отримаємо значення
подвійного інтеграла.
Зауваження
3. Якщо область ![]() правильна в обох напрямах, то подвійний
інтеграл можна обчислювати як за формулою (10), так і за формулою (11). Результати
матимемо однакові.
правильна в обох напрямах, то подвійний
інтеграл можна обчислювати як за формулою (10), так і за формулою (11). Результати
матимемо однакові.
Зауваження
4. Якщо область ![]() не є правильною ні в напрямі осі
не є правильною ні в напрямі осі ![]() , ні в напрямі осі
, ні в напрямі осі ![]() (тобто існують
вертикальні і горизонтальні прямі, які, проходячи через внутрішні точки області,
перетинають її межу більше, ніж у двох точках), то таку область необхідно розбити
на частини, кожна з яких є правильною областю у напрямі
(тобто існують
вертикальні і горизонтальні прямі, які, проходячи через внутрішні точки області,
перетинають її межу більше, ніж у двох точках), то таку область необхідно розбити
на частини, кожна з яких є правильною областю у напрямі ![]() чи
чи
![]() . Обчислюючи подвійні інтеграли по правильних областях і додаючи
результати (властивість адитивності), знаходимо шуканий подвійний інтеграл за областю
. Обчислюючи подвійні інтеграли по правильних областях і додаючи
результати (властивість адитивності), знаходимо шуканий подвійний інтеграл за областю
![]() . Для випадку,
зображеного на рис.6 (область
. Для випадку,
зображеного на рис.6 (область ![]() обмежена еліпсами
обмежена еліпсами  і прямою
і прямою ![]() ), при інтегруванні в напрямі
осі
), при інтегруванні в напрямі
осі ![]() маємо
маємо
![]() .
.
У напрямі осі ![]() тут
потрібно було б обчислити повторні інтеграли по семи областях.
тут
потрібно було б обчислити повторні інтеграли по семи областях.
Зауваження 5. Повторні інтеграли в правих частинах формули (10) і (11) називаються інтегралами з різним порядком інтегрування. Щоб змінити порядок інтегрування, потрібно від формули (10) перейти до формули (11) або навпаки.
У кожному конкретному
випадку, залежно від виду області ![]() та підінтегральної
функції
та підінтегральної
функції ![]() , потрібно
обирати той порядок інтегрування, який призводить до простіших обчислень.
, потрібно
обирати той порядок інтегрування, який призводить до простіших обчислень.
Зауваження
6. Правильну в напрямі осі ![]() область
область ![]() коротко позначатимемо
так:
коротко позначатимемо
так:
![]() .
.
Аналогічно
![]()
область правильна в напрямі
осі ![]() .
.
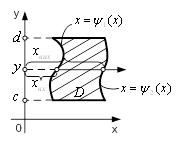
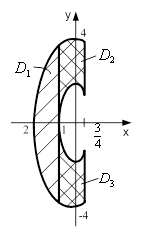
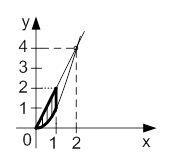
Рисунок 5 - Область ![]() Рисунок 6 - Область
Рисунок 6 - Область ![]() Рисунок 7 - Область
Рисунок 7 - Область
![]()