Контрольная работа: Экономико-математические модели управления
Федеральное агентство по образованию Федеральное образовательное учреждение высшего профессионального образования Нижегородский государственный университет имени Н.И. Лобачевского (ННГУ)
Финансовый факультет
Кафедра: «Налоги и налогообложение»
Контрольная работа
По дисциплине: Менеджмент
Тема: «Экономико-математические модели управления»
Выполнила студентка
заочного отделения 2-го курса
Группа 13н 23
Загорулько А.А.
Проверил: Синцов В.Г.
Нижний Новгород
2010
Содержание
Введение
Глава І Теоретические основы экономико-математических моделей управления
1.1 Основные понятия теории моделирования
1.2 Методология моделирования
1.3 Основные термины экономико-математического моделирования
Глава ІІ Экономико-математическое моделирование в принятии управленческих решений
2.1 Математические модели при принятии решений
2.2 Математический инструментарий принятия решений
Глава ІІІ Частные случаи экономико-математического моделирования в менеджменте
3.1 Экономико-математическое моделирование на примере прогнозирования и планирования
Заключение
Список использованной литературы
Введение
Тема моей контрольной работы - «Экономико-математические модели управления». Экономико-математические модели и методы - представляет собой логический системный подход к решению проблемы управления.
Менеджеру известно, что хорошо структурированные проблемы имеют многовариантные решения, элементы которых, а также связи между ними, хорошо изучены и могут быть выражены количественно. Оптимальное решение для таких проблем может быть найдено с помощью методов исследования операций и экономико-математических моделей. Например, выбор оптимального варианта развития и реконструкции предприятия, расчет оптимальной загрузки производственных мощностей, разработка оптимальных режимов технологических
процессов.
Слабо структурированные проблемы связаны с выработкой долгосрочных курсов действий, каждый из которых затрагивает многие стороны деятельности организации и поэтапно реализуется. Например, определение стратегии технического перевооружения производства, совершенствование организации управления и т.п. Эти проблемы содержат наряду с хорошо изученными, количественно формализуемыми элементами также неизвестные или неизмеряемые компоненты, отличающиеся значительной неопределенностью. Они решаются с помощью методов системно, анализа, сочетающих в себе сложные математические расчеты с большим объемом субъективных суждений руководителей и специалистов.
Неструктуризованные проблемы отличаются значительной неопределенностью и неформализуемостью как самих целей деятельности, так и возможных курсов действий.
Цель контрольной работы состоит в рассмотрении теоретических особенностей:
· Основных понятий теории моделирования;
· Методологии экономико-математического моделирования;
· Основных терминов экономико-математического моделирования;
· Математического инструментария;
· Экономико-математических моделей при принятии управленческих решений.
Задачи работы диктуются поставленной целью:
· Дать определения основных понятий теории моделирования;
· Рассмотреть методологию экономико-математического моделирования;
· Дать определения основных терминов экономико-математического моделирования;
· Рассмотреть математический инструментарий и его применение в решении конкретной задачи;
· Спрогнозировать экономико-математические модели на частном случае.
Глава І Теоретические основы экономико-математических моделей управления
1.1 Основные понятия теории моделирования
Модель (обобщенная модель) - создаваемый с целью получения и (или) хранения информации специфический объект (в форме мысленного образа, описания знаковыми средствами либо материальной системы), отражающий свойства, характеристики и связи объекта-оригинала произвольной природы, существенные для задачи, решаемой субъектом.
Для теории принятия решений наиболее полезны модели, которые выражаются словами или формулами, алгоритмами и иными математическими средствами.
Пример словесной модели.
Обсудим необходимость учета эффекта лояльности при управлении организацией в современных условиях.
Лояльность - честное, добросовестное отношение к чему-либо или к кому-либо.
Базу менеджмента, основанного на лояльности, заложил в 1908 году профессор Гарварда Джошуа Ройс. Он является автором книги «Философия лояльности», где впервые научно определено понятие «лояльность».
В рамках предлагаемой словесной модели бизнес-лояльность рассматривается с точки зрения трех самостоятельных базисных аспектов:
· лояльность потребителей;
· лояльность сотрудников;
· лояльность инвесторов.
Каждый раз за словом «лояльность» понимается:
· приверженность (с точки зрения покупателей);
· добросовестность (с точки зрения сотрудников);
· взаимное доверие, уважение и поддержка (с точки зрения инвесторов).
Несмотря на ярко выраженные компоненты, эта система должна рассматриваться только как единое целое, поскольку невозможно создать лояльных покупателей, не обращая внимания на лояльность сотрудников, или воспитать лояльность сотрудников без должного внимания к лояльности инвесторов. Ни одна из частей не может существовать отдельно от двух других, но все три вместе позволяют организации достигать невиданных высот в развитии.
Необходимо четко понимать, что менеджмент, основанный на лояльности, прежде всего обращен на людей. В первую очередь здесь рассматриваются именно люди и их роль в бизнесе. Это скорее модель мотивации и поведения, чем маркетингового, финансового или производственного развития. Лишь во вторую очередь менеджмент, основанный на лояльности, обобщает людей в более абстрактные категории и управляет техническими процессами.
Как показывает практика, люди всегда оказываются более готовыми работать на организацию, которая имеет цель служения, чем на организацию, которая существует только ради того, чтобы «делать деньги». Поэтому люди охотно работают в церкви или в общественных организациях.
Менеджеры, желающие успешно использовать модель управления, основанную на эффекте лояльности, не должны рассматривать прибыль как первоочередную цель, но как необходимый элемент благосостояния и выживания трех составляющих каждой бизнес-системы:
· покупателей;
· сотрудников;
· инвесторов.
Еще в начале ХХ в. Генри Форд говорил, что «организация не может работать без прибыли, ... иначе она умрет. Но и создавать организацию только ради прибыли ... значит привести ее к верной гибели, так как у нее не будет стимула к существованию».
Основа рассматриваемой модели лояльности - не прибыль, а привлечение дополнительного количества покупателей, процесс, который осознанно или неосознанно лежит в основе большинства преуспевающих организаций. Создание целевого количества покупателей пронизывает все сферы бизнеса компании. Силы, управляющие взаимосвязями между покупателями, сотрудниками и инвесторами, называют силами лояльности.
Критерий успешности - возвращаются ли покупатели, чтобы купить больше, или они идут куда-то еще, т.е. проявляют ли они лояльность.
Как причина лояльность инициирует несколько экономических эффектов, которые влияют на всю бизнес систему следующим образом:
1. Прибыли и рыночная доля растут, когда наиболее перспективные покупатели охватывают весь спектр деятельности компании, создавая о ней хорошее общественное мнение и повторно приходя за покупками. За счет большого и качественного предложения компания может себе позволить быть более привередливой при выборе новых покупателей и концентрироваться на более прибыльных и потенциально лояльных проектах их привлечения, дальше стимулируя свой долгосрочный рост.
2. Долгосрочный рост позволяет фирме привлекать и сохранять лучших сотрудников. Постоянное поддержание целевого количества покупателей увеличивает лояльность сотрудников, давая им чувство гордости и удовлетворения своей работой. В процессе взаимодействия постоянные сотрудники узнают больше о своих постоянных покупателях, как лучше их обслуживать, чтобы объем покупок рос. Этот увеличивающийся объем продаж подстегивает и лояльность покупателей, и лояльность сотрудников.
3. Лояльные сотрудники в долгосрочном периоде учатся снижать издержки и повышать качество работы (эффект научения). Организация может использовать эту дополнительную продуктивность для расширения системы вознаграждения, для покупки лучшего оборудования и обучения. Все это подстегнет продуктивность сотрудников, рост вознаграждений и лояльность.
4. Такая спираль продуктивности дает такое преимущество в издержках, которое очень сложно скопировать для чисто конкурентных организаций. Долгосрочные преимущества в издержках, соединенные с устойчивым ростом количества лояльных покупателей, приносят прибыль, очень привлекательную для инвесторов. Это расширяет возможности компании по привлечению и сохранению “правильных” инвесторов.
5. Лояльные инвесторы ведут себя как партнеры. Они стабилизируют систему, снижают издержки по поиску капитала и дают гарантии, что полученные отвлеченные денежные потоки будут вложены обратно в бизнес как инвестиции. Это укрепляет организацию и увеличивает ее производственный потенциал.
Покупатели - активы любой организации, и для достижения успеха ей необходимо управлять ими также эффективно, как и другими активами. Но для этого нужно быть в состоянии сегментировать покупателей, предсказывать их поведение, а также жизненный цикл их денежных потоков.
В основе большинства провалов лежит общепринятый бизнес-язык организации - бухгалтерский учет, который в настоящий момент ограничивает возможности формирования лояльности. Бухгалтеры не в состоянии провести черту между выручкой, полученной от вновь пришедших покупателей, и выручкой, полученной от постоянных, лояльных покупателей. Это происходит потому, что они не знают, а точнее, их не заботит тот факт, что обслуживание нового покупателя оказывается более дорогим, нежели обслуживание постоянного покупателя. В большинстве организаций бухгалтеры считают вложения в привлечение покупателей краткосрочными. И это вместо того, чтобы относить их на специальный счет покупателя и амортизировать в течение всего времени отношений с ним.
Итак, как же сформировать портфель лояльных покупателей? Существует два варианта действий:
· первый - увеличение списка покупателей. Организация постоянно добавляет новых покупателей к началу списка, но ее старые покупатели также постоянно вымываются снизу из этого списка. Получается эффект дырявой корзины. Чем больше в ней дыра, тем тяжелее ее наполнить и сохранять наполненной.
· второй - заключен в эффекте прибыли от каждого покупателя. В большинстве организаций прибыль, которую приносит каждый покупатель, растет, пока он остается ее клиентом. Для организации невыгодно терять постоянных покупателей, даже заменяя их новыми. Получается ситуация, когда «за одного битого двух небитых дают».
При подборе покупателей необходимо помнить, что существует три основных типа лояльных покупателей. Это помогает определить, сможет ли организация сделать покупателя лояльным:
1. Некоторые покупатели изначально предсказуемы и лояльны, вне зависимости от того, как организация с ними работает. Они просто лояльны по природе своей. Они предпочитают более стабильные и длительные отношения.
2. Некоторые покупатели более прибыльны, чем другие. Они тратят деньги в большем количестве, чем другие, оплачивают покупки безотлагательно и требуют меньше внимания обслуживающего персонала.
3. Некоторые покупатели находят продукты или услуги организации (в силу их особенностей) более привлекательными, чем у конкурентов. Нет такой организации, товары которой нравились бы всем без исключения. Сильные стороны ее товаров или услуг будут просто лучше подходить для определенных покупателей, более полно удовлетворяя их желаниям и возможностям.
Каждая организация уникальна, но все же в той или иной мере показатели ее прибылей будут укладываться в общую модель экономических эффектов, получаемых от постоянства или лояльности покупателей.
Среди них стоит особо отметить следующие:
v издержки привлечения (реклама, направленная новым покупателям, комиссионные по продажам новым покупателям, накладные расходы продаж и т.д.);
v базовая прибыль (цена, которую платят вновь появившиеся покупатели, превышает затраты организации на создание товара);
v рост выручки (как правило, если покупатель доволен параметрами товара, он склонен увеличивать объемы покупок с течением времени);
v издержки сбережений (близкое знакомство с товарами организации уменьшает зависимость покупателей от ее сотрудников в вопросах информации и советов);
v отзывы (удовлетворенные уровнем обслуживания покупатели рекомендуют организацию своим друзьям и знакомым);
v дополнительная цена (постоянные покупатели, сотрудничающие с организацией достаточно долго, чтобы изучить все ее товары и услуги, получают несоизмеримо больше от продолжения отношений и не нуждаются в дополнительных скидках или рекламных акциях).
Чтобы оценить истинный долгосрочный потенциал лояльности покупателя или группы покупателей, необходимо знать их предрасположенность к проявлению постоянства. Так некоторые покупатели перебегут к конкуренту и за 2% скидку, а другие останутся и при 20% разнице в цене.
Количество усилий, которое требуется для переманивания различных типов покупателей, называется коэффициентом лояльности. В некоторых организациях для оценки коэффициентов лояльности используется история развития или поведение покупателей на отдельных сегментах. В других, особенно в тех, чье будущее слабо связано с прошлым, пытаются методами анализа данных нащупать, на сколько велика должна быть скидка, чтобы покупатели перешли к их организации. Но, несмотря на все трудности в измерении, использование коэффициента лояльности позволяет организациям идентифицировать сохранение покупателей и внедрять оправданную практику, проверенную на одном департаменте, во всю организацию.
Развитие систем измерения, анализа и управления денежными потоками, полученными от лояльности, может привести организацию к инвестициям, которые в дальнейшем обеспечат рост количества покупателей и организации в целом.
Модель лояльности подробно обоснована на словесном уровне. В этом обосновании упоминалось математическое и компьютерное обеспечение. Однако для принятия первоначальных решений их использование не требуется.
1.2 Методология моделирования
математическая модель управленческое решение
Моделирование процессов управления предполагает последовательное осуществление трех этапов исследования:
· первый - от исходной практической проблемы до теоретической чисто математической задачи;
· второй - внутриматематическое изучение и решение этой задачи;
· третий - переход от математических выводов обратно к практической проблеме.
В области моделирования процессов управления целесообразно выделять четверки составляющих (рис. 1.1):

Рис.1.1 Составляющие области моделирования
Обсудим каждую из только что выделенных составляющих.
Задача порождена потребностями той или иной прикладной области. При этом происходит одна из возможных математических формализаций реальной ситуации. Например, при изучении предпочтений потребителей у экономистов - маркетологов возникает вопрос: различаются ли мнения двух групп потребителей. При математической формализации мнения потребителей в каждой группе обычно моделируются как независимые случайные выборки, т.е. как совокупности независимых одинаково распределенных случайных величин, а вопрос маркетологов переформулируется в рамках этой модели как вопрос о проверке той или иной статистической гипотезы однородности. Речь может идти об однородности характеристик, например, о проверке равенства математических ожиданий, или о полной (абсолютной однородности), т.е. о совпадении функций распределения, соответствующих двух совокупностям.
Задача может быть порождена также обобщением потребностей ряда прикладных областей. Приведенный выше пример иллюстрирует эту ситуацию: к необходимости проверки гипотезы однородности приходят и медики при сравнении двух групп пациентов, и инженеры при сопоставлении результатов обработки деталей двумя способами, и т.д. Одна и та же математическая модель может применяться для решения самых разных по своей прикладной сущности задач.
Выделение перечня задач находится вне математики. Этот перечень является сутью технического задания, которое специалисты различных областей деятельности дают специалистам по математическому моделированию.
Метод, используемый в рамках определенной математической модели - это дело математиков.
В эконометрических моделях речь идет о методе оценивания, о методе проверки гипотезы, о методе доказательства той или иной теоремы, и т.д.
Для решения той или иной задачи в рамках одной и той же принятой исследователем модели может быть предложено много методов. Приведем примеры. Для специалистов по теории вероятностей и математической статистике наиболее хорошо известна история Центральной Предельной Теоремы теории вероятностей. Предельный нормальный закон был получен многими разными методами, из которых напомним теорему Муавра-Лапласа, метод моментов Чебышева, метод характеристических функций Ляпунова, завершающие эпопею методы, примененные Линдебергом и Феллером.
В настоящее время для решения практически важных задач могут быть использованы современные информационные технологии на основе метода статистических испытаний и соответствующих датчиков псевдослучайных чисел. Они потеснили асимптотические методы математической статистики. В рассмотренной выше проблеме однородности для проверки одной и той же гипотезы совпадения функций распределения могут быть применены самые разные методы - Смирнова, Лемана - Розенблатта, Вилкоксона и др.
Последний элемент четверки - условия применимости. Он - полностью внутриматематический. С точки зрения математика замена условия (кусочной) дифференцируемости некоторой функции на условие ее непрерывности может представляться существенным научным достижением, в то время как прикладник оценить это достижение не сможет. Для него, как и во времена Ньютона и Лейбница, непрерывные функции мало отличаются от (кусочно) дифференцируемых. Точнее, они одинаково хорошо (или одинаково плохо) могут быть использованы для описания реальной действительности.
Методологический анализ - первый этап моделирования процессов управления, любого исследования. Он определяет исходные постановки для теоретической проработки, а потому во многом и успех всего исследования. Анализ динамики развития методов моделирования позволяет выделить наиболее перспективные методы. При вероятностно-статистическом моделировании наиболее перспективными оказались методы нечисловой статистики.
1.3 Основные термины математического моделирования
Прежде чем начать рассматривать конкретные математические модели процессов управления, необходимо дать определения основных терминов:
· компоненты системы - части системы, которые могут быть вычленены из нее и рассмотрены отдельно;
· независимые переменные - они могут изменяться, но это внешние величины, не зависящие от проходящих в системе процессов;
· зависимые переменные - значения этих переменных есть результат (функция) воздействия на систему независимых внешних переменных;
· управляемые (управляющие) переменные - те, значения которых могут изменяться исследователем;
· эндогенные переменные - их значения определяются в ходе деятельности компонент системы (т.е. «внутри» системы);
· экзогенные переменные - определяются либо исследователем, либо извне, т.е. в любом случае действуют на систему извне.
При построении любой модели процесса управления желательно придерживаться следующего плана действий:
1) Сформулировать цели изучения системы;
2) Выбрать те факторы, компоненты и переменные, которые являются наиболее существенными для данной задачи;
3) Учесть тем или иным способом посторонние, не включенные в модель факторы;
4) Осуществить оценку результатов, проверку модели, оценку полноты модели.
Модели можно разделить на виды (рис. 1.2):
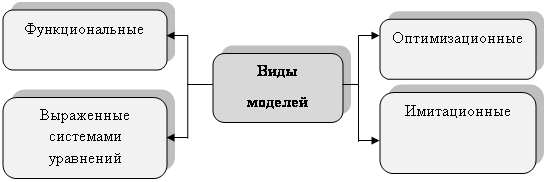
Рис. 1.2 Виды моделей
Их определения:
v Функциональные модели - выражают прямые зависимости между эндогенными и экзогенными переменными.
v Модели, выраженные с помощью систем уравнений относительно эндогенных величин. Выражают балансовые соотношения между различными экономическими показателями (например, модель межотраслевого баланса).
v Модели оптимизационного типа. Основная часть модели - система уравнений относительно эндогенных переменных. Цель - найти оптимальное решение для некоторого экономического показателя (например, найти такие величины ставок налогов, чтобы обеспечить максимальный приток средств в бюджет за заданный промежуток времени).
v Имитационные модели - весьма точное отображение экономического явления. Математические уравнения при этом могут содержать сложные, нелинейные, стохастические зависимости.
С другой стороны, модели можно делить на управляемые и прогнозные. Управляемые модели отвечают на вопрос: «Что будет, если ...?»; «Как достичь желаемого?», и содержат три группы переменных:
1) переменные, характеризующие текущее состояние объекта;
2) управляющие воздействия - переменные, влияющие на изменение этого состояния и поддающиеся целенаправленному выбору;
3) исходные данные и внешние воздействия, т.е. параметры, задаваемые извне, и начальные параметры.
В прогнозных моделях управление не выделено явно. Они отвечают на вопросы: «Что будет, если все останется по-старому?»
Модели можно делить по способу измерения времени на:
· непрерывные;
· дискретные.
Если в модели присутствует время, то модель называется динамической. Чаще всего в моделях используется дискретное время, т.к. информация поступает дискретно: отчеты, балансы и иные документы составляются периодически. Но с формальной точки зрения непрерывная модель может оказаться более простой для изучения. В физической науке продолжается дискуссия о том, является ли реальное физическое время непрерывным или дискретным.
Обычно в достаточно крупные социально-экономические модели входят материальный, финансовый и социальный разделы.
Материальный раздел - балансы продуктов, производственных мощностей, трудовых, природных ресурсов. Это раздел, описывающий основополагающие процессы, это уровень, обычно слабо подвластный управлению, особенно быстрому, поскольку весьма инерционен.
Финансовый раздел содержит балансы денежных потоков, правила формирования и использования фондов, правила ценообразования и.т.п. На этом уровне можно выделить много управляемых переменных. Они могут быть регуляторами. Социальный раздел содержит сведения о поведении людей. Этот раздел вносит в модели принятия решений много неопределенностей, поскольку трудно точно правильно учесть такие факторы как трудоотдача, структура потребления, мотивация и.т.п.
При построении моделей, использующих дискретное время, часто применяют методы эконометрики. Среди них популярны регрессионные уравнения и их системы. Часто используют лаги (запаздывания в реакции). Для систем, нелинейных по параметрам, применение метода наименьших квадратов встречает трудности.
Глава ІІ Экономико-математические модели при принятии управленческих решений
2.1 Математические модели при принятии решений
При принятии решений в менеджменте производственных систем используются:
· модели технологических процессов (модели контроля и управления);
· модели обеспечения качества продукции (модели оценки и контроля надежности);
· модели массового обслуживания;
· модели управления запасами (модели логистики);
· имитационные и эконометрические модели деятельности предприятия в целом, и др.
Можно выделить такие этапы процесса принятия и реализации решения (рис. 1.3):

Рис. 1.3 Этапы процесса принятия и реализации решения
Приведенная последовательность этапов процесса принятия и реализации решения не означает, что руководитель обязан выполнить все эти этапы и подэтапы, чтобы прийти к хорошему решению.
Ряд из подэтапов может быть опущен. Цель и задача могут быть очевидны или заданы (например, в приказе «разработать к данному числу проект мероприятий» цель и задача даны). Альтернативных вариантов в силу ряда причин (например, отсутствия необходимой информации) может не быть. Задача может быть столь стандартна, что нет нужды придумывать что-то новое, и руководитель просто использует уже встречавшийся ему способ деятельности, что снимает необходимость в проведении этапа «выбора окончательного решения».
Выделение этапов и подэтапов процесса принятия и реализации решения позволяет:
v легче отбирать, анализировать и оценивать как сами возможные варианты
решений, так и мотивы, побудившие их выбрать;
v легко находить причину затруднений в выработке решений;
v легко определить причины отклонений в ходе реализации решения;
v проанализировать склонности руководителя к использованию тех или иных способов и средств решения проблем с целью обучения.
Не следует рассматривать приведенную последовательность как заданную раз и навсегда. Эти этапы в ряде случаев проходят перпендикулярно, а не параллельно или сплетаются еще более сложными способами.
Проблема возникает обычно под воздействием внешней среды из-за несовершенства протекания самих материально-вещественных процессов, когда их результаты отклоняются от запланированных параметров, т.е. когда имеет место разрыв между желаемым состоянием системы (целью) и ее фактическим состоянием.
Процесс управления в этом случае рассматривается как последовательное принятие решений по возникающим проблемам.
Проблемы могут быть разделены на четыре типа:
· стандартные;
· хорошо структурированные;
· слабо структурированные;
· неструктурированные.
Решение стандартных проблем отличается ясностью и однозначностью целей, альтернатив и требуемых затрат. Для разработки их применяются заранее выработанные процедуры и правила, например, известные методики составления бизнес-плана, расчет потребности в оборудовании, в материалах, в рабочей силе, исходя из заданной производственной программы.
При решении неструктуризованных проблем суждения, опыт, интуиция руководителей и квалифицированных специалистов приобретает решающее значение.
Правильная организация экспертных спросов, квалифицированная обработка данных, четкая формулировка руководящих и основополагающих правил для решения проблем во многом обеспечивают выработку рациональных решений.
Стандартные и хорошо структуризованные проблемы относятся к числу программируемых, а слабо структуризованные и неструктуризованные проблемы являются непрограммируемыми.
Вместе с тем даже в принятии программируемых решений роль субъектного фактора, искусства руководителей и специалистов достаточно велика.
Целесообразно различать два аспекта работы по подготовке решений. Один из них касается «конструирования» самого проекта, его моделирования, другой -соответствующих процедурных правил и организационных мероприятий.
Выбор методов подготовки и обоснования решения зависит от характера решаемых проблем.
Сообразно вышеприведенной классификации могут быть использованы и четыре типа методов решения проблем:
· стандартные процедуры и правила определения решений;
· экономико-математические методы поиска оптимальных решений;
· системный анализ для построения рациональных альтернатив;
· экспертно-интуитивные методы принятия решений.
Поскольку решения направлены прежде всего на поиск и разрешение задач в той или иной обстановке, внимание во многом концентрируется на новых методах их разработках. Отсюда попытки некоторой формализации встречающихся ситуаций, которая позволяет типизировать их и определять наиболее характерные признаки.
В результате осмысливания проблемы порождается цель (иногда цели) будущего решения и его содержание.
Методы выбора и обоснование рациональных решений являются важнейшим компонентом процесса принятия решения в управлении. Усложнение управленческих ситуаций, резкое возрастание объемов информации, на основании которой принимается решение, требуют использования экономико-математических методов и компьютеризации процесса анализа и выбора решения.
Методы выбора решения сами по себе еще не гарантируют правильности решения.
Различают две группы методов выбора решений:
- методы нахождения решения путем формализации задачи и дальнейшего ее решения средствами математики;
- методы выбора решения, имеющие эвристическую оценку, т.е. такие методы выбора решения, которые базируются на интуитивно-логических заключениях.
По мере совершенствования формальных методов управления роль человека в принятии решений не только не уменьшается, но и возрастает, поскольку он высвобождается от выполнения работы формализуемых процедур.
При принятии решения очень важно обеспечить правильное сочетание формальных и неформальных методов, максимально использовать те возможности, которые несет с собой автоматизация процессов принятия решений, но и не следует переоценивать эти возможности.
Моделирование заключается в том, что создается модель, т.е. нечто похожее на реальную систему и сохраняющие существенные свойства ее как оригинала.
Модели могут быть:
· физическими;
· аналоговыми;
· математическими.
Физическая модель представляет то, что исследуется с помощью увеличенного или уменьшенного описания объекта или системы.
Аналоговая модель представляет собой исследуемый объект аналогом, который ведет себя как реальный объект, но не выглядит как таковой.
Математические модели характеризуют реальную систему символическими уравнениями или неравенствами.
Универсальность математического языка делает математические модели наиболее удобным инструментом изучения объекта, его основных свойств.
Применение математических методов для подготовки решений имеет несколько этапов:
· определяется круг проблем, подлежащих решению, причем должна быть четко сформулирована цель решения;
· разбивается на составные части - постоянные и переменные величины;
· требуется формализовать задачу и построить модель, которая выражает качественное содержание явлений через количественные характеристики.
Вторая часть модели - ее ограничение - представляет собой математическую запись условий, при которых осуществляется выбор решения.
После того как модель построена, начинается ее экономико-математический анализ, основной целью которого является нахождение оптимального решения.
Моделирование может охватывать все виды аналитических действий, совершаемых при непосредственной подготовке решений.
Каждый вид моделирования – это способ, метод возможного отображения социально-экономических процессов и отыскания на основе определенных критериев и оценок оптимального варианта решения. Модели могут применяться как относительно самостоятельно, так и в сочетании друг с другом, в виде системы моделей.
На выбор оптимального варианта решения влияет и информация. Информация необходима как для разработки и принятия решений, так и для насыщения управляющей системы такими исходными данными, которые позволяют сформулировать и осуществить управляющее воздействие, команду. Соотношение между ними всегда должно быть в пользу времени и труда, затрачиваемого на обработку информации. В противном случае принятие решений превратится в беспрерывный механический процесс. Информация необходима и на стадии реализации решения.
Важное значение имеет своевременность сбора и обработки информации. Нельзя допускать преждевременного сбора информации, когда еще не созрели условия для появления факта или изменения обстановки. Равным образом недопустимо проводить сбор и анализ информации с опозданием.
«Баланс» информации и решений достигается благодаря поиску и установлению обоснованной меры информации для каждого органа управления, соответствующей выполняемым им функциям. Необходимо также увязывать виды и объем информации по отдельным функциям вышестоящих и нижестоящих органов. Несовпадение каналов и видов собираемой информации ведет к тому, что вышестоящее звено «собирает» от нижестоящих такую информацию, которую оно не «накапливает» для себя.
Иногда еще до сбора всей информации уже можно предвидеть цель и основное содержание решения, тогда роль информации сводится к более точному их обоснованию. Но чаще всего именно анализ информации позволяет выявить обоснования и цели решений, определить их направленность и т.п.
Полнота, объективность и оптимальность информации позволяют наиболее правильно оценить все фактические данные, выработать варианты решений и выбрать оптимальные из них.
Моделирование позволяет заранее предвидеть ход событий и тенденции развития, присущие управляемой системе, выяснить условия ее существования и установить режим деятельности с учетом влияния разных факторов.
2.2 Математический инструментарий принятия решений
Этот инструментарий (экономико-математические модели и методы - ЭМММ) представляет собой логический системный подход к решению проблемы управления. Схематически его можно изобразить, как это показано на рис. 1.4.
С точки зрения ЭМММ центральным моментом становится конструирование модели - абстрактного представления существующей проблемной ситуации. Обычно такая модель представляется в виде математического соотношения или графика.

Рис. 1.4 Использование ЭМММ при принятии решения
Предположим, фирма продает продукт по цене 20$, а его себестоимость - 5$. Полная прибыль: z = 20x-5x,
где x - число проданных единиц продукта, x и z - переменные, причем x - независимая, z - зависимая переменная; числа 20 и 5 - параметры.
Это соотношение - модель определения прибыли фирмы. Предположим, что продукт делается из стали и что фирма имеет 100 кг стали в своем распоряжении. На единицу продукта идет 4 кг стали. Следовательно, 4x = 100 кг.
Теперь модель выглядит так:
z = 20x - 5x. (1)
4x = 100. (2)
Здесь уравнение (1) - целевая функция, а уравнение ресурсов (2) - ограничение, то есть управленческое решение будет моделироваться так:
max z = 20x - 5x при 4x = 100.
Итак, если менеджер решает продать 25 единиц продукта (x = 25), фирма получит прибыль z = 375$. Эта величина не действительное решение, а скорее информация, которая служит рекомендацией или руководством, помогающим менеджеру принять решение.
Некоторые модели не дают ответа и рекомендаций по решению. Однако они обеспечивают описательные результаты: эти результаты описывают моделируемую систему (например, дисперсия продаж некоторых товаров по месяцам в течение года).
Менеджер не прямо применяет полученный результат как решение, а сопоставляет его со своими оценками и прогнозами. Если менеджер не использует результаты ЭМММ, то они нереализуемы. Если это так, то должны быть введены дополнительные ресурсы или усилия при решении проблемы, конструировании модели и ее решении.
Результаты моделирования и решения основаны на сравнении путем обратной связи с первоначальной моделью, которая может модифицироваться при испытаниях в различных условиях и будущих решениях менеджера. Результаты могут указывать, что проблема полностью не охвачена ранее и это требует изменений или реконструкции первоначальной модели. В этом случае ЭМММ представляют непрерывный процесс, а не одиночное решение одиночной проблемы.
Классификация ЭМММ приведена на рис. 1.5. Далее содержится краткая оценка их практической применимости в современном менеджменте.
Наиболее популярна техника линейного программирования. К ней проводят задачи, связанные с ограничениями (по ресурсам, времени, рабочей силе, энергии, финансам, материалам) и с целевой функцией типа максимизации прибыли. Существенным является линейность функциональных соотношений в математической модели. Конкретная техника решений состоит в использовании алгоритма последовательных шагов (т. е. программы).
При использовании вероятностных процедур, в отличие от линейного программирования, результаты носят вероятностный характер и должны содержать некоторую неопределенность и возможность присутствия альтернативных решений.
Процедуры управления запасами специально разработаны для анализа проблем запасов, что характерно для большинства коммерческих фирм. Эта частная функция управления вносит существенный вклад в издержки любого бизнеса.
Сетевые модели скорее более диаграммы, чем точные математические соотношения. Они представляют в наглядной форме систему действий для их анализа.
Другие процедуры являются многоступенчатыми (программными), но отличными по постановке от линейной задачи.
В практическом менеджменте наибольшее значение придается:
- имитационным моделям;
- линейному программированию;
- графам (деревьям) решений;
- сетевым моделям;
- теории очередей (задачам массового обслуживания);
- анализу замещения;
- интегральному программированию.

Рис. 1.5 Классификация ЭМММ
Частота использования различных методов респондентами отражена в табл.1.1:
Таблица 1.1
Доля респондентов, использующих конкретные методы
| Сфера управления | % респондентов |
| Статистический анализ | 98,4 |
| Имитация на компьютерах | 87,1 |
| Сетевые методы | 74,1 |
| Линейное программирование | 74,2 |
| Теория очередей | 59,7 |
| Нелинейное программирование | 46,8 |
| Динамическое программирование | 38,7 |
| Теория игр | 30,6 |
Следует отметить определенную переоценку значимости экономико-математических моделей в реальной практике управления экономико-производственными системами. Это связано с непреодолимыми пока сложностями моделирования процессов в экономико-производственных системах из-за непрерывности изменений продукции, нерегулярности производства, внутренних дестабилизирующих факторов, нерегулярности снабжения, финансирования, сбыта и т.д.
Большинство этих факторов носит нестационарный характер, что фактически исключает возможность использования эконометрических моделей в планировании и управлении реальным производством.
Экономико-математические модели отражают наиболее существенные свойства реального объекта или процесса с помощью системы уравнений. Единой классификации экономико-математических моделей также не существует, хотя можно выделить наиболее значимые их группы в зависимости от признака классификации.
По степени агрегирования объектов моделирования различают модели:
· микроэкономические;
· одно-, двухсекторные (одно-, двухпродуктовые);
· многосекторные (многопродуктовые);
· макроэкономические;
· глобальные.
По учету фактора времени модели подразделяются на:
· статические;
· динамические.
В статических моделях экономическая система описана в статике, применительно к одному определенному моменту времени. Это как бы снимок, срез, фрагмент динамической системы в какой-то момент времени. Динамические модели описывают экономическую систему в развитии.
По цели создания и применения различают модели:
· балансовые;
· эконометрические;
· оптимизационные;
· сетевые;
· систем массового обслуживания;
· имитационные (экспертные).
По учету фактора неопределенности модели подразделяются на:
· детерминированные (с однозначно определенными результатами);
· стохастические (с различными, вероятностными результатами).
По типу математического аппарата различают модели:
· линейного и нелинейного программирования;
· корреляционно-регрессионные;
· матричные;
· сетевые;
· теории игр;
· теории массового обслуживания и т.д.
Глава ІІІ Частные случаи экономико-математического моделирования в менеджменте
3.1 Экономико-математическое моделирование на примере прогнозирования и планирования
Прогнозирование - это взгляд в будущее, оценка возможных путей развития, последствий тех или иных решений.
Планирование - это разработка последовательности действий, позволяющей достигнуть желаемого.
В работе менеджера они тесно связаны. Разберем простой пример, показывающий взаимосвязь прогнозирования и планирования.
Представим, что вы находитесь в степи, а ваша максимальная скорость ходьбы - 6 километров в час. Тогда можно предсказать, что через час вы будете находиться в какой-то точке круга радиуса 6 километров с центром в начальной точке. Результаты прогнозирования вы можете использовать для планирования. Если место, куда вы направляетесь, отстоит от начальной точки не более чем на 6 километров, то вы доберетесь туда пешком не более чем за час. Если же это расстояние - 18 километров, то прогноз показывает невозможность решения поставленной задачи. Что же делать? Либо отказаться от своего намерения, либо увеличить выделенной время (до 3 часов), либо воспользоваться более быстрым транспортным средством, чем ноги (автомобилем, вертолетом). Иногда прогноз основан на хорошо изученных закономерностях и осуществляется наверняка. Встающие перед менеджером проблемы прогнозирования обычно не позволяют дать однозначный обоснованный прогноз. Почему же остается неопределенность?
Рассмотрим классификацию различных видов неопределенностей. Часть связана с недостаточностью знаний о природных явлениях и процессах, например:
· неопределенности, связанные с недостаточными знаниями о природе;
· неопределенности природных явлений, таких, как погода, влияющая на урожайность, на затраты на отопление, на туризм, на загрузку транспортных путей и др.;
· неопределенности, связанные с осуществлением действующих (неожиданные аварии) и проектируемых (возможные ошибки разработчиков или физическая невозможность осуществления процесса, которую заранее не удалось предсказать) технологических процессов.
Возможные неопределенности связаны с ближайшим окружением фирмы, менеджер которой занимается прогнозированием:
v неопределенности, связанные с деятельностью участников экономической жизни (прежде всего партнеров и конкурентов нашей фирмы), с их деловой активностью, финансовым положением, соблюдением обязательств;
v неопределенности, связанные с социальными и административными факторами в конкретных регионах, в которых фирма имеет деловые интересы.
Большое значение имеют неопределенности на уровне страны:
v неопределенность будущей рыночной ситуации в стране, отсутствие достоверной информации о будущих действиях поставщиков в связи с меняющимися предпочтениями потребителей;
v неопределенности, связанные с колебаниями цен (динамикой инфляции), нормы процента, валютных курсов и других макроэкономических показателей;
v неопределенности, порожденные нестабильностью законодательства и текущей экономической политики (т.е. с деятельностью руководства страны, министерств и ведомств), связанные с политической ситуацией, действиями партий, профсоюзов, экологических и других организаций в масштабе страны.
Приходится учитывать и внешнеэкономические неопределенности, связанные с ситуацией в зарубежных странах и международных организациях, с которыми поддерживаются деловые отношения.
Менеджеру приходится прогнозировать будущее, принимать решения и действовать при таком наборе неопределенностей.
Введём их классификацию на СТЭП-факторы (по первым буквам от слов - социальные, технологические, экономические, политические) и факторы конкурентного окружения.
СТЭП-факторы действуют независимо от менеджера, а вот конкуренты к фирме не безразличны. Возможно, они будут бороться, стремиться к вытеснению фирмы с рынка. Но возможны и переговоры, ведущие к обоюдовыгодной договоренности. Каждая из перечисленных видов неопределенности может быть структуризована. Имеются крупные разработки по анализу неопределенностей при технологических авариях, в частности, на химических производствах и на атомных электростанциях. Аварии типа Чернобыльской существенно влияют на значения СТЭП-факторов и на поступления и выплаты из бюджета как на местном, так и на федеральном уровне. Прогнозы всегда опираются на некоторые предположения. Наиболее обычным является предположение стабильности: «если существующие тенденции и связи сохранятся», «если не произойдет ничего необычного»... Иногда надо спрогнозировать развитие интересующего процесса как раз в необычных условиях. Например, что произойдет с экономикой России в целом и с фирмой, если будут отменены все таможенные сборы и пошлины на экспорт и импорт, т.е. Россия перейдет к политике «свободной торговли», пропагандируемой во многих американских учебниках по экономике?
Если рассмотреть ситуацию, в которой события могут развиваться по нескольким принципиально различным вариантам, то применяют метод сценариев.
Метод сценариев - это метод декомпозиции (т.е. упрощения) задачи прогнозирования, предусматривающий выделение набора отдельных вариантов развития событий (сценариев), охватывающих все возможные варианты развития. Каждый отдельный сценарий должен допускать возможность достаточно точного прогнозирования, а общее число сценариев - быть обозримым.
В конкретной ситуации сама возможность подобной декомпозиции не всегда очевидна. При применении метода сценариев необходимо осуществить два этапа исследования:
v построение исчерпывающего, но обозримого набора сценариев;
v прогнозирование в рамках каждого конкретного сценария с целью получения
ответов на интересующие менеджера вопросы.
Каждый из этих этапов лишь частично формализуем.
Некоторые прогнозы имеют свойство самоосуществляться. Само их высказывание способствует их осуществлению. Например, высказанный по телевидению прогноз банкротства конкретного банка приводит к тому, что многие вкладчики сразу заявляют о желании забрать свои вклады из этого банка. Но ни один банк не может вернуть вклады одновременно всем вкладчикам или даже достаточно большой их доле (например, 4 из 10), поскольку часть средств выдана в качестве кредитов, часть вложена в ценные бумаги той или иной степени ликвидности, часть истрачена на содержание банка (здание, компьютеры, зарплата сотрудников, ...). В результате банк действительно оказывается банкротом..
Один из вариантов применения методов прогнозирования - выявление необходимости изменений путем «приведения к абсурду». Если население Земли каждые 100 лет будет увеличиваться вдвое, то нетрудно подсчитать, через сколько лет на каждый квадратный метр поверхности Земли будет приходиться по 10000 человек. Из такого прогноза следует, что закономерности роста численности населения должны измениться.
Учет нежелательных тенденций, выявленных при прогнозировании, позволяет принять необходимые меры для их предупреждения, а тем самым помешать осуществлению прогноза.
Прогнозирование - частный вид моделирования как основы познания и управления.
Простейшие методы восстановления зависимостей в детерминированном случае исходят из заданного временного ряда, т.е. функции, определенной в конечном числе точек на оси времени. Временной ряд часто рассматривается в рамках вероятностной модели, вводятся иные факторы (независимые переменные), помимо времени, например, объем денежной массы (агрегат М2).
Временной ряд может быть многомерным, т.е. число откликов (зависимых переменных) может быть больше одного. Основные решаемые задачи - интерполяция и экстраполяция (т.е. собственно прогноз). Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан немецким математиком К.Гауссом в 1794-1795 гг. Могут оказаться полезными предварительные преобразования переменных. Для игроков на финансовых рынках такой подход называется «техническим анализом».
Опыт прогнозирования индекса инфляции и стоимости потребительской корзины накоплен в Лаборатории эконометрических исследований Московского государственного института электроники и математики (технического университета). При этом оказалось полезным преобразование (логарифмирование) переменной - текущего индекса инфляции. При стабильности условий точность прогнозирования оказывалась достаточно удовлетворительной - 10-15 %. Однако спрогнозированное значительное повышение уровня цен не осуществилось. Дело в том, что руководство страны перешло к стратегии сдерживания роста потребительских цен путем массовой невыплаты зарплаты и пенсий. Условия изменились - и статистический прогноз оказался непригодным.
Для применения статистических методов прогнозирования нужны длинные временные ряды. Альтернативой статистическим методам служат экспертные методы прогнозирования, опирающиеся на опыт и интуицию специалистов.
Для прогнозирования могут использоваться также эконометрические и экономико-математические модели, а также создаваться специальные компьютерные системы, позволяющие совместно применять все перечисленные методы. Целью является учет всех возможных факторов, с помощью которых есть надежда улучшить прогноз. Для игроков на финансовых рынках такой подход называется «фундаментальным анализом».
Заключение
Исходя из проведенных мною исследований данной темы, я пришла к выводу, что моделирование позволяет заранее предвидеть ход событий и тенденции развития, присущие управляемой системе, выяснить условия ее существования и установить режим деятельности с учетом влияния разных факторов. При этом, может показаться, что чем большее количество факторов учтено в модели, тем лучше сама модель. На самом деле детализированная модель не всегда целесообразна, так как это излишне усложняет модель и труднее ее анализировать.
Может оказаться, что решение, оптимальное для системы в целом, является неоптимальным для отдельных частей этой системы – ее подразделений. Поэтому вместе с оптимальными решениями должен быть продуман механизм, позволяющий сделать его оптимальным для всех участников.
Существует проблема адекватности критерия оптимальности целям функционирования моделируемой системы. Например, точная формулировка цели не всегда дает возможность сформулировать критерий оптимальности. Другая проблема связана с неоднозначностью определения самой цели. При использовании экономико-математических методов обычно принято считать, что существует единственный критерий оптимизации. Однако организация может иметь несколько.
Если цели не противоречат друг другу, то достижение одной из них не мешает выполнению других. Например, цель увеличения прибыли и максимизация выпуска продукции не противоречивы. В то же время максимизировать выпуск и одновременно затраты невозможно. В задачах с несколькими критериями оптимальности «оптимальное» решение не всегда бывает единственным. Поэтому сужается проблема выбора, и в этом случае для окончательного решения требуется неформальный подход.
Список использованной литературы
1. Справочник директора предприятия. - М.,1997;
2. Менеджмент: учебник / Э.М. Коротков. – М.: Издательство Юрайт, 2010, - 640 с. – (Университеты России);
3. Акофф Р. Планирование будущего корпорации. – М.: Прогресс, 1985;
4. Антикризисное управление: учебник / под редакцией Э.М. Короткова. – М.: Инфра-М, 2000;
5. Годин В.В. Информационное обеспечение управленческой деятельности / В.В Годин, И.К. Корнеев. – М.: Мастерство, Высшая школа, 2001;
6. Глухов В. Менеджмент: учебник для вузов. – СПб.: Питер, 2007;
7. В. Бугера. Собственность и управление (философско-экономические очерки). – М.: МАИК-Наука, 2003;
8. Евланов Л.Г. Принятие решений в условиях неопределенности. – М., 1976;
9. Информационные системы в экономике / коллектив авт., под ред. В.В. Година. – М.: ГУУ, 2006;
10. Междисциплинарный словарь по менеджменту. – М.: Дело, 2007;
11. Прохоров А.П. Русская модель управления. – М.: Эксмо, 2006;
12. Мильнер Б.З. Организационные структуры управления производством. – М.,1980;
13. Менеджмент. Учебник. / А.И.Орлов.- М.: Издательство «Изумруд», 2003. - 298 с.;
14. Д.К. Лафта. Эффективность менеджмента организации. – М.: Дело, 1999.