Курсовая работа: Интегралы, зависящие от параметра
Министерство образования и науки РФ
Федеральное Агентство по образованию
ГОУ ПВО «Таганрогский государственный педагогический институт»
Курсовая работа
на тему: Интегралы, зависящие от параметра
Таганрог. 2009 г.
Введение
Математический анализ - общеобразовательная математическая дисциплина, объектом изучения которой является большая часть математики, связанная с понятиями функции, производной и интеграла. Цель дисциплины «Математический анализ»- ознакомление с фундаментальными методами исследования переменных величин посредством анализа бесконечно малых, основу которого составляет теория дифференциального и интегрального исчисления.
Объектами изучения в данной дисциплине являются прежде всего функции. С их помощью могут быть сформулированы как законы природы, так и разнообразные процессы, происходящие в технике. Отсюда объективная важность математического анализа как изучения функций. 2 Интегралы, зависящие от параметра.
1.![]() Несобственные интегралы
Несобственные интегралы
Несобственные интегралы первого рода.
Пусть f :[a, +![]() R и интегрируема
по Риману на любом отрезке [a, A] (A
R и интегрируема
по Риману на любом отрезке [a, A] (A![]() (а,
(а,![]()
![]() Формальное выражение
Формальное выражение
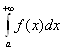
назовем несобственным интегралом первого рода.
Определени2.1 Несобственный интеграл первого рода назовем сходящимся, если существует
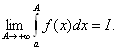
В этом случае будем говорить, что число I является значением интеграла и писать
![]()
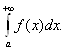
Если же указанный предел равен бесконечности или вовсе не существует, то будем говорить, что интеграл расходится.
При аналогичных предложениях определим несобственные интегралы
![]() и
и ![]()
Пример.2.1. Исследовать на сходимость интеграл
![]()
∆Пусть ![]() тогда
тогда
![]()
Если ![]() , то существует конечный
, то существует конечный
![]() то есть
интеграл J сходится, причем
то есть
интеграл J сходится, причем ![]() Если
Если ![]() то
то ![]() и поэтому интеграл J расходится.
При
и поэтому интеграл J расходится.
При ![]() интеграл
также расходится, так как
интеграл
также расходится, так как ![]() при
при ![]()
Таким образом, интеграл J
сходится при ![]() и расходится при
и расходится при ![]() ▲
▲
Теорема 2.1(критерий Коши) Для сходимости несобственного интеграла
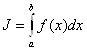
Необходимо и достаточно, чтобы выполнялось условие Коши
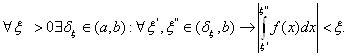 (1)
(1)
Обозначим
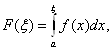
![]() (2)
(2)
Тогда сходимость
интеграла J означает существование конечного предела функции ![]() при
при ![]() а этот предел, согласно
критерию Коши для функций, существует в том и только том случае, когда функция
F удовлетворяет условию
а этот предел, согласно
критерию Коши для функций, существует в том и только том случае, когда функция
F удовлетворяет условию
![]() (3)
(3)
Из формулы (2) в силу свойств интеграла следует, что
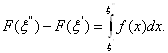
Поэтому условие (3),
являясь необходимым и достаточным для сходимости интеграла J, выполняется тогда
и только тогда, когда выполняется условие (1), если взять ![]() ●
●
Если использовать определение предела функции по Гейне, то можно сформулировать
Предложение 2.1  сходится тогда
и только тогда, когда
сходится тогда
и только тогда, когда
для любой
последовательности ![]() →+∞, последовательность
интегралов
→+∞, последовательность
интегралов 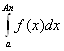 сходится.
сходится.
Определение 2. 2. Назовем
интеграл  абсолютно
сходящимся, если сходится интеграл
абсолютно
сходящимся, если сходится интеграл 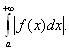
Теорема 2.2. Если  сходится
абсолютно, то он сходится.
сходится
абсолютно, то он сходится.
Доказательство. Так как
интеграл сходится абсолютно, то по критерию Коши ![]() выполняется условие
выполняется условие
![]()
Но тогда и
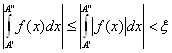
При любых ![]() ■
■
Определение 2.3. Если сходится, но
не сходится абсолют-
сходится, но
не сходится абсолют-
но, то будем называть его условно сходящимся.
Теорема 2.3
(Вейерштрасс). Пусть функции f, g: [а; +∞) →R, интегрируемы по
Риману на [а; А] при любом А > а, ![]() для всех
для всех ![]() и
и 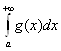 сходится. Тогда
сходится. Тогда  тоже сходится и притом
абсолютно.
тоже сходится и притом
абсолютно.
Доказательство. Так как 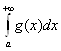 сходится, то
по критерию Коши
сходится, то
по критерию Коши
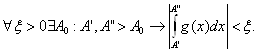
Но тогда при А’, А” > ![]() имеем:
имеем:
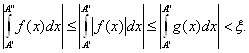
Из полученной оценки, в силу критерия Коми, вытекает и сходимость и абсолютная сходимость интеграла от f(x) •
Замечание 2.1.
Неравенство ![]() в
формулировке теоремы может выполняться лишь для
в
формулировке теоремы может выполняться лишь для ![]() , где b>a. Это
вытекает из того, что всегда можно представить
, где b>a. Это
вытекает из того, что всегда можно представить 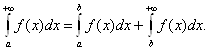
Первый интеграл в этом представлении не особенный, а ко второму можно применить доказанную теорему.
Пример 2.2 Рассмотрим интегралы
![]()
Решение. Так как ![]() а
а ![]() сходится, если
р> 1 (пример2.1) то и
сходится, если
р> 1 (пример2.1) то и ![]() сходится, и притом абсолютно, при
р > 1. Второй интеграл рассматривается аналогично.
сходится, и притом абсолютно, при
р > 1. Второй интеграл рассматривается аналогично.
Теорема 2.4 (Дирихле)
Пусть функции f, g: ![]() и интегрируемы по Риману на [а;
А] при любом А > а. Тогда
и интегрируемы по Риману на [а;
А] при любом А > а. Тогда 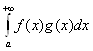 сходится, если выполнены следующие
два условия:
сходится, если выполнены следующие
два условия:
1) 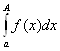 ограничен на [а; +∞);
ограничен на [а; +∞);
2) функция g(x) монотонно
стремится к нулю при ![]()
Доказательство. По
первому условию существует постоянная М такая, что 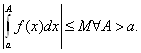 .
.
По второму условию ![]() такое, что при
А >
такое, что при
А > ![]() будет
выполняться неравенство
будет
выполняться неравенство ![]() . По второму же условию функцию
g(x) можно считать неотрицательной. Возьмём
. По второму же условию функцию
g(x) можно считать неотрицательной. Возьмём ![]() и применим к интегралу
и применим к интегралу ![]() вторую теорему о среднем значении
(формулу Боннэ), согласно которой найдётся
вторую теорему о среднем значении
(формулу Боннэ), согласно которой найдётся ![]() такое, что
такое, что
![]()
Но тогда, поскольку
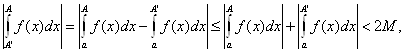
справедлива оценка
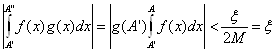
для любых А’, А” > ![]() . По критерию
Коши интеграл сходится.
. По критерию
Коши интеграл сходится.
Теорема 2.5 (Абель) Пусть
функции f, g : [а; +∞)→R и интегрируемы по Риману на [а; А] при
любом А > а. Тогда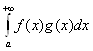 сходится, если выполнены
следующие два условия:
сходится, если выполнены
следующие два условия:
1) 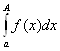 сходится;
сходится;
2) функция g(x) монотонна и ограничена на [а; +∞).
Доказательство. В силу
второго условия существует![]() .
.
Тогда 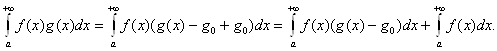
Первый из интегралов справа сходится по признаку Дирихле, поскольку
![]() монотонно стремится к нулю при х→+∞,
а второй сходится в силу условия 1 доказываемой теоремы. ■
монотонно стремится к нулю при х→+∞,
а второй сходится в силу условия 1 доказываемой теоремы. ■
Замечание 2.2 При доказательстве теоремы Абеля было использовано очевидное свойство
несобственных интегралов:
если сходятся интегралы 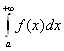 и
и 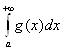 , то сходится и
, то сходится и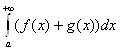 , при этом
, при этом 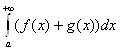 =
=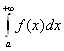 +
+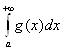
Пример 2.3 Вернемся к
рассмотренным выше примерам ![]()
Решение. По признаку
Дирихле эти интегралы сходятся при р > 0, поскольку при этом условии дробь ![]() ↓ 0, а
интегралы
↓ 0, а
интегралы ![]()
![]() очевидно,
ограничены.
очевидно,
ограничены.
Пример 2.4 Рассмотрим![]()
Решение. Этот интеграл
сходится по признаку Абеля. Действительно, сходимость интеграла ![]() установлена в
предыдущем примере, а
установлена в
предыдущем примере, а
функция arctg х монотонна и ограничена. ■ Несобственные интегралы второго рода
Пусть функция f : (а; b] →R, неограниченна в окрестности точки а, но интегрируема по Риману на [а + δ, b] при любом 0<δ<b-a.
Формальное выражение 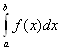 назовём
несобственным интегралом второго рода.
назовём
несобственным интегралом второго рода.
Определение 2.4 Несобственный интеграл второго рода назовём сходящимся, если существует
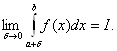
В этом случае будем говорить, что число I являемся значением интеграла и писать
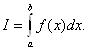
Если же указанный предел равен бесконечности или вовсе не существует, то будем говорить, что интеграл расходится. Аналогично определяется
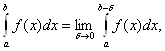
если функция f определена на [а; b), интегрируема на [а; b-ξ] при любом 0<δ<b-a и неограниченна в окрестности точки b.
Если же функция f определена на [а; b]\{c}, а < с < b, неограниченна в окрестности точки с, но интегрируема на отрезках [а; с-δ] и [с-δ; b] при любом допустимом положительном δ, то определим
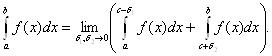
Пример 2.5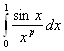 сходится при р<1 и
расходится при р
сходится при р<1 и
расходится при р![]() .
.
Теорема 2.6 (критерий
Коши) Если функция f: (a; b]→R, неограниченна в окрестности точки а, но
интегрируема по Риману на [а + δ, b] при любом О<δ<δ-a, то
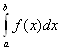 сходится
тогда и только тогда, когда
сходится
тогда и только тогда, когда ![]() такое, что
такое, что ![]() а’, а” : а <а’, а”
< а + δ. Будет выполняться условие
а’, а” : а <а’, а”
< а + δ. Будет выполняться условие 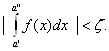
Это утверждение доказывается так же, как и аналогичное утверждение для несобственных интегралов первого рода. Так же вводится понятие абсолютной и условной сходимости и устанавливается соотношение между ними. Так же формулируется и доказывается признак сходимости Вейерштрасса. Интегралы в смысле главного значения
Определение 2.5 Пусть
функция f: R→ R, интегрируема по Риману на любом конечном отрезке, но
несобственный интеграл ![]() не существует. Тогда, если существует
не существует. Тогда, если существует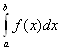 , мо он
называется интегралом в смысле главного значения и обозначается символом
, мо он
называется интегралом в смысле главного значения и обозначается символом
(![]() p.)
p.) ![]()
Определение 2.6 Пусть функция f: [а;b ]\{с} → R, а <с < b, неограниченна в окрестности точки с, интегрируема по Риману на отрезках
[а; с — δ] и [с +
δ; b] при любом δ> 0, но 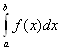 не существует. Тогда, если
существует
не существует. Тогда, если
существует 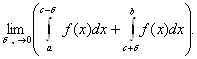 то
он называется интегралом в смысле главного значения н обозначаемся символом (
то
он называется интегралом в смысле главного значения н обозначаемся символом (![]() p.)
p.) 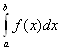
Пример 2.6 Рассмотрим ![]()
Решение. Это — расходящийся интеграл второго рода, поскольку показатель степени p =1. Однако
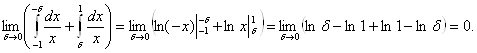
Следовательно, рассматриваемый интеграл существует в смысле главного значения и
(![]() p.)
p.) ![]()
Пример 2.7 Рассмотрим ![]()
Решение. Этот интеграл
расходится, так как подынтегральная функция f(х)~![]() .
.
Но ![]()
Следовательно, этот
интеграл существует в смысле главного значения и (![]() p.)
p.) ![]()
Собственные интегралы, зависящие от параметра
Пусть f: [а; b] х Y →
R, где [а; b] ![]() R, Y- любое множество,
R, Y- любое множество,
а [а; b] х Y = {(х, у): х
![]() [а; b], у
[а; b], у![]() Y}. Предположим, что
Y}. Предположим, что ![]() функция f интегрируема по Риману
на отрезке [а; b].
функция f интегрируема по Риману
на отрезке [а; b].
Определение 2.7 Функцию
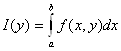 (2.1)
(2.1)
определённую на множестве Y при описанных выше условиях, будем называть собственным интегралом, зависящим от параметра. Изучим свойства этого интеграла, ограничившись простейшим случаем:
У = [с; d] ![]() R, и введя обозначение
R, и введя обозначение
П [а b] х [с; d] = {(х,
у): х ![]() [а;
b], у
[а;
b], у ![]() [с;
d]}.
[с;
d]}.
Теорема 2.7 Пусть функция f непрерывна на прямоугольнике П. Тогда функция I(у) непрерывна на отрезке [а; b].
Доказательство. Функция
непрерывна на множестве, если она непрерывна в каждой точке множества. Возьмём,
поэтому, любое ![]() [с; d] и
[с; d] и
любое ![]() > 0 и покажем, что
найдётся
> 0 и покажем, что
найдётся ![]() >
0 такое, что если у
>
0 такое, что если у ![]() [с; d] и
[с; d] и
![]() , то будет выполняться неравенство
, то будет выполняться неравенство
![]() Прямоугольник
П — компактное множество в
Прямоугольник
П — компактное множество в ![]() , поэтому по теореме
, поэтому по теореме
Кантора функция f
равномерно непрерывна на П, следовательно, по выбранному ![]() >0 можно указать
такое
>0 можно указать
такое ![]() >
0, что если
>
0, что если
![]()
то будет выполняться неравенство
![]()
Положим х' = х"= х,
у' = у, у" =![]() . Тогда
. Тогда
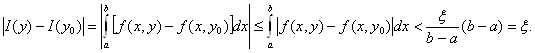
Полученная оценка
доказывает не только непрерывность, но и равномерную (поскольку δ не
зависит от ![]() )
непрерывность функции I(у) на отрезке [а; b].■
)
непрерывность функции I(у) на отрезке [а; b].■
Теорема 2.8 Пусть функция f непрерывна на прямоугольнике П. Тогда функция I(у) интегрируема на отрезке [с; d] и справедливо равенство
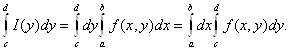 (2.2)
(2.2)
Доказательство.
Интегрируемость I(у) вытекает из предыдущей теоремы и теоремы об
интегрируемости непрерывных функций. Равенство же 2.2 следует из теоремы о
сведении кратного интеграла к повторному. для непрерывной на прямоугольнике П
функции существует ![]() , который может быть сведен к
повторному в любом порядке.
, который может быть сведен к
повторному в любом порядке.
Теорема 2.9 Если функция
f непрерывна и имеет непрерывную частную производную ![]() на прямоугольнике П, то функция
I(у) дифференцируема на отрезке [с; d] и справедливо равенство
на прямоугольнике П, то функция
I(у) дифференцируема на отрезке [с; d] и справедливо равенство
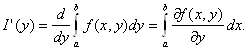 (2.3)
(2.3)
Доказательство. Так как ![]() непрерывна на
П, то, используя предыдущую теорему, для любого у
непрерывна на
П, то, используя предыдущую теорему, для любого у ![]() [с; d] можем написать равенство
[с; d] можем написать равенство
 (2.4)
(2.4)
Упростим левую часть равенства 2.4 с помощью формулы Ньютона-Лейбница.
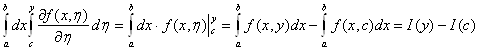
Обозначим через J(η) внутренний интеграл в правой части равенства (2.4). Тогда равенство (2.4) примет вид:
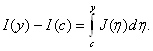 (2.5)
(2.5)
По теореме 2.7 J(η) — непрерывная на [с; d] функция. Но тогда по теореме о производной интеграла с переменным верхним пределом правая часть равенства (3.5) (следовательно, и левая) дифференцируема на отрезке [с; d]. По той же теореме из равенства (3.5) получаем:
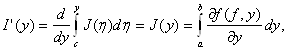
что и требовалось. ■
Рассмотрим теперь более общий случай, когда не только подынтегральная функция,
но и пределы интегрирования зависят от параметра. Итак, пусть функция f(x, у)
определена на прямоугольнике П =[а; Ь] х [с; d], интегрируема по х на отрезке
[а; b] для каждого у ![]() [с; d], функции а (у) и b(у)
заданы на отрезке [с; d] и
[с; d], функции а (у) и b(у)
заданы на отрезке [с; d] и ![]() [с; d] выполняется а ≤ а(у)
≤ b(у) ≤ b. Рассмотрим интеграл
[с; d] выполняется а ≤ а(у)
≤ b(у) ≤ b. Рассмотрим интеграл
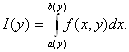 (2.6)
(2.6)
Теорема 2.10 Пусть функция f(x, у) непрерывна на П, а функции а(у), b(у) непрерывны на [с; d]. Тогда функция I(у), определённая равенством (2.6),непрерывна на [с; d].
Доказательство. Пусть y ![]() [с; d].
Покажем, что
[с; d].
Покажем, что ![]() Для этого разобьём интеграл на три
слагаемых, используя свойство аддитивности интеграла.
Для этого разобьём интеграл на три
слагаемых, используя свойство аддитивности интеграла.
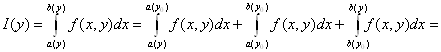
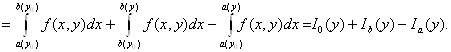 (2.7)
(2.7)
Здесь интегралы
обозначены в порядке следования. Рассмотрим каждый из них в отдельности. Первый
из интегралов — интеграл с постоянными пределами вида 2.1, его непрерывность
доказана в теореме 2.7. Поэтому ![]()
Займемся вторым интегралом. Функция f(x, у) непрерывна на П, следовательно, ограничена. Поэтому существует постоянная М такая, что
![]() П.
П.
Но тогда
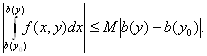
А так как функция b(у)
непрерывна на [с; d], то ![]() при
при ![]() , поэтому
, поэтому ![]()
Совершенно аналогично
доказывается, что и ![]()
Таким образом,
![]()
что и требовалось доказать.
Теорема 2.11 Пусть функция f непрерывна на прямоугольнике П и
имеет на нём непрерывную
частную производную ![]() , а функции а(у) и
, а функции а(у) и
b(у) дифференцируемы на отрезке [с; d]. Тогда функция I(у), определяемая равенством (2.6), дифференцируема на отрезке [с; d] и её производная может быть вычислена по формуле
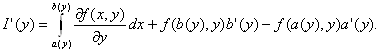 (2.8)
(2.8)
Доказательство. Поскольку
дифференцируемость на промежутке есть дифференцируемость в каждой точке
промежутка, то возьмём ![]() на отрезке [с; d] и покажем, что I(у) дифференцируема в точке
на отрезке [с; d] и покажем, что I(у) дифференцируема в точке ![]() , и что
, и что ![]() представляется
в виде правой части формулы (2.8). Для этого воспользуемся представлением I(у) в виде (2.7) и покажем, что
каждое слагаемое
представляется
в виде правой части формулы (2.8). Для этого воспользуемся представлением I(у) в виде (2.7) и покажем, что
каждое слагаемое
правой части (2.7) дифференцируемо и вычислим его производную. Первый из интегралов в правой части (2.7) имеет постоянные пределы
интегрирования. Его дифференцируемость установлена в теореме 2.9.
Поэтому
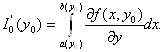 (2.9)
(2.9)
Теперь докажем
дифференцируемость и вычислим производную второго слагаемого в правой части (2.7).
(Отметим, что ![]() .) По определению производной
.) По определению производной
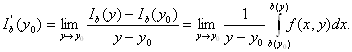
Так как подынтегральная функция непрерывна (по х), то по свойству
определённого интеграла
найдётся с = с(у), ![]() , такое, что
, такое, что
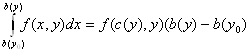 .
.
Но тогда
![]()
![]()
так как первый предел существует по теореме о трёх функциях и в силу непрерывности функции f на прямоугольнике П, а второй — в силу
дифференцируемости функции b(у). Итак,
![]() . (2.10)
. (2.10)
Совершенно аналогично доказывается, что третье слагаемое в (2.7) дифференцируемо и что
![]() . (2.11)
. (2.11)
Итак, все три слагаемых в
правой части равенства (2.7) дифференцируемы в точке ![]() , значит, и функция I(у) дифференцируема в точке
, значит, и функция I(у) дифференцируема в точке ![]() и
и ![]() . (2.12)
. (2.12)
Подставив сюда значения
производных (формулы (2.9), (2.10), (2.11)), получим представление (2.8) в
точке ![]() .■
.■
Замечание 2.3 Условия теорем 2.7 — 2.11 являются достаточными.
декларируемые в теоремах свойства могут выполняться и при нарушении условий этих теорем. Но быть уверенным в их выполнении при нарушении условий теорем нельзя. Рассмотрим соответствующие примеры.
Пример 2.8 Рассмотрим 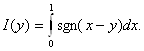
Решение. Подынтегральная функция на прямой у = х терпит разрыв.
Однако, вычислив интеграл, убедимся, что он представляет непрерывную функцию от у на всей вещественной прямой.
1. Пусть у≤ 0.
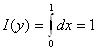 ;
;
2.Пусть о< у <1.
I(у)=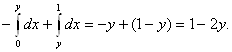
3.Пусть у ≥ 1. 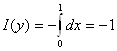 Нетрудно
убедиться, что функция ‚ I(у) имеет одинаковые пределы
Нетрудно
убедиться, что функция ‚ I(у) имеет одинаковые пределы
слева и справа в точках у
= 0 и у = 1, поэтому непрерывна. Пример 2.9 Рассмотрим 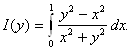
Решение. Подынтегральная функция терпит разрыв в точке (0; 0), однако, вычислив интеграл, убедимся, что он представляет интегрируемую
на отрезке [0; 1] функцию.
несобственный интеграл параметр непрерывность
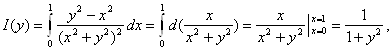
поэтому
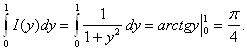
Однако попытка проинтегрировать по параметру под знаком интеграла приведёт к иному результату.
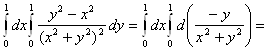
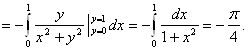 ■
■
Пример 2.10 Рассмотрим 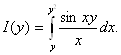
Решение. Легко видеть, что интеграл удовлетворяет условиям теоремы 2.11 на любом отрезке [с; d]. Найдём производную I’(y), используя формулу 2.8.
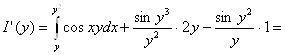
![]()
![]()
Несобственные интегралы, зависящие от параметра
Пусть Y — произвольное
множество, f: [а; +∞) х Y → R. Предположим, что для каждого у ![]() сходится
сходится 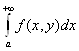 .
.
Тогда на множестве
Y определена функция
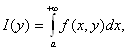 (2.13)
(2.13)
которую будем называть несобственным интегралом первого рода, зависящим от параметра.
Равномерная сходимость
Понятие равномерной сходимости для несобственных интегралов, зависящих от параметра, столь же важно, как и для функциональных рядов.
Определение 2.8 Будем
говорить, что интеграл (2.13) сходится равномерно на множестве Y, если его остаток равномерно
стремится к нулю на этом множестве, то есть, если ![]() такое, что
такое, что ![]() выполняется неравенство
выполняется неравенство
![]() (2.14)
(2.14)
Теорема 2.12 (критерий
Коши) для того, чтобы интеграл (2.13) сходился равномерно на множестве Y, необходимо и достаточно выполнение следующего
условия (условие Коши): ![]() , зависящее
, зависящее
только от ![]() , такое, что
, такое, что ![]() будет
выполняться неравенство
будет
выполняться неравенство
![]() (2.15)
(2.15)
Доказательство. Пусть
интеграл (2.13) сходится равномерно на множестве Y. Тогда, взяв любое ![]() > 0, подберем
> 0, подберем ![]() так, чтобы для
так, чтобы для
любых А> А![]() и у
и у![]() выполнялось
неравенство
выполнялось
неравенство ![]() .
.
Возьмём любые ![]() и любое у
и любое у![]() . Тогда
. Тогда
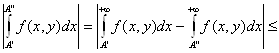
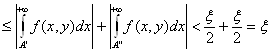
и необходимость доказана.
Наоборот, если выполнено
условие (2.15), то оно выполнено для любого фиксированного у![]() . Но тогда по теореме
2.1 для любого фиксированного у
. Но тогда по теореме
2.1 для любого фиксированного у ![]() интеграл (2.13) сходится, то
есть, для каждого у
интеграл (2.13) сходится, то
есть, для каждого у ![]() существует
существует 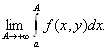 Поэтому, положив в (2.15)
Поэтому, положив в (2.15)
![]() и устремив
А" к +∞, получим для любого у
и устремив
А" к +∞, получим для любого у ![]()
![]()
что означает равномерную на Y сходимость интеграла (2.13).
Теорема 2.13 (Вейерштрасс) Пусть f: [a, +∞) → R и для любых
А(> а) и у![]() функция f
интегрируема по Риману на отрезке [а; A].
функция f
интегрируема по Риману на отрезке [а; A].
Пусть g : [а; +∞) →R,
для всех х ![]() [а;
+∞), у
[а;
+∞), у ![]() выполняется неравенство
выполняется неравенство ![]() и
и 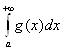 сходится.
Тогда интеграл (2.13) сходится равномерно (и абсолютно) на множестве Y.
сходится.
Тогда интеграл (2.13) сходится равномерно (и абсолютно) на множестве Y.
Доказательство. По критерию
Коши для несобственных интегралов первого рода (см. 2.1) для любого![]() > 0
найдётся
> 0
найдётся ![]() такое,
что для любых
такое,
что для любых ![]() будет выполняться неравенство
будет выполняться неравенство 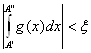 Но тогда для
любого у
Но тогда для
любого у![]() ,
для любых
,
для любых![]() имеем:
имеем:
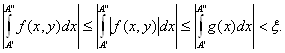
Остаётся применить теорему 2.12. .
Пример 2.11 Рассмотрим 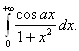
Решение. Этот интеграл сходится равномерно на R, так как имеет место
Оценка ![]() а
а 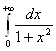 сходится. ■
сходится. ■
Теорема 2.14 (Дирихле) Пусть функции f, g: [а; +∞) х Y→ R и
интегрируемы по Риману на
[а; А] при любых А > а и у![]() .
.
Тогда 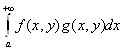 сходится равномерно на
Y, если выполнены следующие два условия:
сходится равномерно на
Y, если выполнены следующие два условия:
1)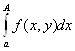 равномерно
ограничен на [а; +∞), то есть, существует постоянная М такая, что для
любых А> а и у
равномерно
ограничен на [а; +∞), то есть, существует постоянная М такая, что для
любых А> а и у ![]()

2)функция у(х, у)
монотонно по х при каждом у![]() и равномерно по у
и равномерно по у![]() стремимся к нулю при х→+∞.
стремимся к нулю при х→+∞.
Доказательство. Доказательство этой теоремы такое же, как и доказательство теоремы 2.4, нужно лишь проследить, чтобы все оценки выполнялись равномерно по параметру. По первому условию существует постоянная М такая, что для всех
A> а и у![]() имеет место оценка:
имеет место оценка:
 (2.16)
(2.16)
По второму условию для любого
![]() > 0
найдётся
> 0
найдётся ![]() (>
а) такое, что
(>
а) такое, что
для любых А> ![]() и у
и у![]() выполнено
выполнено
![]() (2.17)
(2.17)
Возьмём![]() и применим к интегралу
и применим к интегралу![]() вторую
теорему о среднем значении (только на этот раз в общем виде, поскольку неизвестен
знак g(х, у)), согласно которой найдётся А = А(у), А
вторую
теорему о среднем значении (только на этот раз в общем виде, поскольку неизвестен
знак g(х, у)), согласно которой найдётся А = А(у), А ![]() [А’, А”], такое, что
[А’, А”], такое, что
![]() (2.18)
(2.18)
Оценим (2.18) с помощью (2.16) и (2.17).
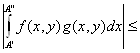
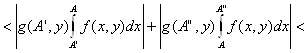
![]()
для любого у из множества Y. Используя критерий Коши, получаем требуемое утверждение. ■
Теорема 2.15 (Абель) Пусть функции f, g : [а; +∞) х Y→R и
интегрируемы по Риману на
[а; А] при любых А > а и у![]() . Тогда
. Тогда 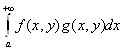 сходимся равномерно на Y, если
выполнены следующие два условия:
сходимся равномерно на Y, если
выполнены следующие два условия:
1) 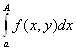 сходимся равномерно на
множестве Y;
сходимся равномерно на
множестве Y;
2)функция g(х, у)
монотонна по х при каждом у![]() и равномерно
и равномерно
по у ![]() ограничена, то есть,
существует постоянная М такая, что
ограничена, то есть,
существует постоянная М такая, что
![]() для всех х
для всех х ![]() [а; +∞) и у
[а; +∞) и у![]() .
.
Пример 2.12 Рассмотрим 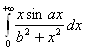 , где b> 0
постоянная, а параметр а удовлетворяет условию
, где b> 0
постоянная, а параметр а удовлетворяет условию ![]()
Решение. Положим f(x,a)=
sinax, g(x,a) ![]() Тогда
Тогда
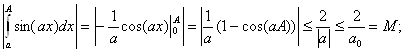
![]()
при х → +∞, и это условие (ввиду независимости функции g от а) выполнено равномерно по а. Так как оба условия признака Дирихле выполнены, то рассматриваемый интеграл сходится равномерно в указанной области.
Пример 2.13 Рассмотрим 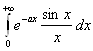 (a≥0)
(a≥0)
Решение. Положим f(x, а)
= ![]() , g(х,
а) =
, g(х,
а) = ![]() . Так
как
. Так
как 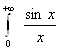
сходится равномерно по а
(ввиду его отсутствия) по признаку Дирихле, а функция ![]() , очевидно, монотонна по х и при х
≥ 0, у ≥0 ограничена, то рассматриваемый интеграл сходится
равномерно в указанной области по признаку Абеля. 2.4 Свойства
несобственных интегралов, зависящих от параметра.
, очевидно, монотонна по х и при х
≥ 0, у ≥0 ограничена, то рассматриваемый интеграл сходится
равномерно в указанной области по признаку Абеля. 2.4 Свойства
несобственных интегралов, зависящих от параметра.
Изучим свойства несобственных интегралов первого рода, зависящих от параметра, ограничившись простейшим случаем: множество Y есть отрезок [с; d] вещественной оси. Введём обозначение
![]()
и докажем предварительно следующую лемму.
Лемма 2.1 Если интеграл (2.13) сходится равномерно на множестве Y
то последовательность функций
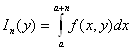 ,(
,(![]() ) (2.19)
) (2.19)
тоже равномерно сходится на множестве Y к функции I(y).
Теорема 2.16 Если функция
f(x, у) определена и непрерывна на П![]() , а интеграл (2.13) сходится равномерно
на отрезке [с; d], мо функция I(у),
определяемая этим интегралом, непрерывна на [с; d].
, а интеграл (2.13) сходится равномерно
на отрезке [с; d], мо функция I(у),
определяемая этим интегралом, непрерывна на [с; d].
Доказательство. По
теореме 2.7 функции I![]() (y) (n
(y) (n ![]() N) непрерывны на отрезке [с; d].
По лемме 2.1 последовательность функций I
N) непрерывны на отрезке [с; d].
По лемме 2.1 последовательность функций I![]() (y) (n
(y) (n ![]() N) сходится равномерно на отрезке
[с; d] к функции ‚I(у). Но тогда по
теореме о пределе равномерно сходящейся последовательности непрерывных функций
функция I(у) непрерывна на отрезке [с; d].
N) сходится равномерно на отрезке
[с; d] к функции ‚I(у). Но тогда по
теореме о пределе равномерно сходящейся последовательности непрерывных функций
функция I(у) непрерывна на отрезке [с; d].
Следующая теорема является в некотором роде обратной к предыдущей.
Теорема 2.17 (Дини) Если
функция f(x, у) непрерывна и неотрицательна П![]() , а функция I(у), определяемая интегралом (2.13),
непрерывна на отрезке [с; d], то интеграл (2.13) сходится равномерно на отрезке
[с; d].
, а функция I(у), определяемая интегралом (2.13),
непрерывна на отрезке [с; d], то интеграл (2.13) сходится равномерно на отрезке
[с; d].
Доказательство. По
теореме 2.7 функции I![]() (y) (n
(y) (n ![]() N) (см. (2.19)) непрерывны на
отрезке [с; d]. Так как функция f(x, у) неотрицательна, то последовательность
функций I
N) (см. (2.19)) непрерывны на
отрезке [с; d]. Так как функция f(x, у) неотрицательна, то последовательность
функций I![]() (y)
(n
(y)
(n ![]() N) монотонно
не убывает.
N) монотонно
не убывает.
Но тогда, поскольку
предельная функция ‚I(у) этой
последовательности тоже непрерывна, к ней можно применить теорему Дини для
последовательностей, согласно которой последовательность I![]() (у) сходится к функции
I(у) равномерно на отрезке [с; d]. Последнее означает, что для любого
(у) сходится к функции
I(у) равномерно на отрезке [с; d]. Последнее означает, что для любого ![]() > 0
найдётся номер n
> 0
найдётся номер n![]() такой, что при n > n
такой, что при n > n![]() для всех у
для всех у ![]() [с; d] справедливо
неравенство
[с; d] справедливо
неравенство ![]() .
.
Положим ![]() и возьмём
и возьмём ![]() . Тогда,
учитывая неотрицательность функции f(x, y), для всех у
. Тогда,
учитывая неотрицательность функции f(x, y), для всех у ![]() получаем:
получаем:
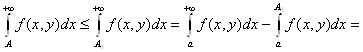
![]()
и равномерная сходимость интеграла доказана.
Теорема 2.18 Если функция f(x, у) определена и непрерывна на а интеграл (2.13) сходится равномерно на отрезке [с; d], то функция I(у), определяемая этим интегралом, интегрируема на [с; d] и справедливо равенство
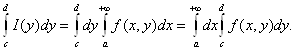 (2.20)
(2.20)
Доказательство. Снова рассмотрим
последовательность I![]() (у). По лемме 2.1 она сходится
равномерно на отрезке [с; d] к функции I(у), а по теореме 2.8 функции последовательности интегрируемы
на отрезке [с; d].
(у). По лемме 2.1 она сходится
равномерно на отрезке [с; d] к функции I(у), а по теореме 2.8 функции последовательности интегрируемы
на отрезке [с; d].
Тогда по теореме об интегрируемости предельной функции равномерно
сходящейся последовательности функция I(у) интегрируема на отрезке [с; d] и
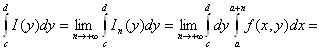
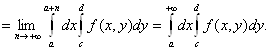
Возможность изменения порядка интегрирования следует из той же теоремы 2.8.
Теорема 2.19 Ecли функция
f(x, у) непрерывна на множестве П![]() и
и
имеет на нём непрерывную
частную производную ![]() (х, y), интеграл (2.13) сходится,
а интеграл
(х, y), интеграл (2.13) сходится,
а интеграл
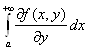 (2.21)
(2.21)
сходится равномерно на [с; d], то функция I(у) дифференцируема на отрезке [с; d] и справедливо равенство
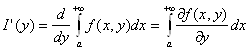 (2.22)
(2.22)
Доказательство. Рассмотрим
последовательность функций I![]() (y). По условию теоремы эта
последовательность сходится на отрезке [с; d] (поскольку сходится интеграл
(2.13)). По теореме 2.9 функции I
(y). По условию теоремы эта
последовательность сходится на отрезке [с; d] (поскольку сходится интеграл
(2.13)). По теореме 2.9 функции I![]() (у) (
(у) (![]() N) дифференцируемы на отрезке [с;
d], а по лемме 2.1 последовательность производных I
N) дифференцируемы на отрезке [с;
d], а по лемме 2.1 последовательность производных I![]() (у) сходится на этом отрезке
равномерно. Но тогда по теореме о дифференцируемости предельной функции
равномерно сходящейся последовательности функция I(у) дифференцируема на
отрезке [с; d]
(у) сходится на этом отрезке
равномерно. Но тогда по теореме о дифференцируемости предельной функции
равномерно сходящейся последовательности функция I(у) дифференцируема на
отрезке [с; d]
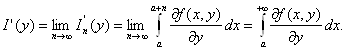
В некоторых случаях бывает необходимо изменить порядок интегрирования, когда и переменная х и параметр у изменяются на бесконечных промежутках. Пусть
![]()
Теорема 2.20 Пусть функция f(x, у) непрерывна и неотрицательна на К. Интегралы
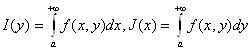 (2.23)
(2.23)
оба сходятся и являются непрерывными функциями соответственно на [с; +∞) и [а; +∞). Тогда равенство
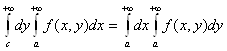 (2.24)
(2.24)
справедливо при условии существования одного из повторных интегралов.
Доказательство. Допустим, что существует левый из интегралов в равенстве (2.24). Покажем, что в таком случае существует и правый интеграл, и что они равны. Для этого достаточно установить, что для любого
с > 0 найдётся А![]() такое, что для
любого А> А
такое, что для
любого А> А![]() будет выполняться неравенство
будет выполняться неравенство
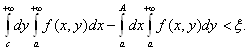 (2.25)
(2.25)
Преобразуем левую часть (2.25). Так как для интеграла
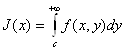
выполнены условия теоремы Дини (теорема 2.17), то он равномерно сходится на любом сегменте [а; А], следовательно по теореме 2.18
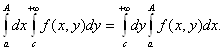
Поэтому
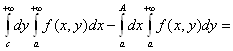
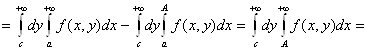
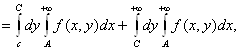
где число С пока не определено.
Выберем ![]() > О и оценим оба
последних интеграла. Так как
> О и оценим оба
последних интеграла. Так как
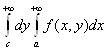
сходится, найдётся С![]() такое, что для
любого С> С
такое, что для
любого С> С![]() будет иметь место неравенство
будет иметь место неравенство
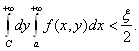
Но тогда, ввиду неотрицательности функции f (x, y), каково бы ни было
А ≥ а, и
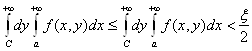 (2.26)
(2.26)
Выберем и зафиксируем С
> С![]() и
оценим первый интеграл. По теореме Дини
и
оценим первый интеграл. По теореме Дини 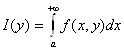 сходится равномерно на отрезке [с;
С],
сходится равномерно на отрезке [с;
С],
поэтому существует ![]() такое, что
если А>
такое, что
если А>![]() , то для любого у
, то для любого у![]() [с; С]
[с; С]
![]()
Поэтому
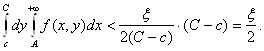 (2.27)
(2.27)
Оценка (2.25) получена, следовательно, теорема доказана. ■
Вычисление интегралов, зависящих от параметра Рассмотрим интеграл, зависящий от параметра α:
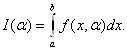
Укажем без
доказательства, что если функция f(x,α) непрерывна по x на отрезке ![]() , то функция
, то функция
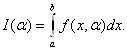
Является непрерывной
функцией на отрезке ![]() . Следовательно, функцию I(α)
можно интегрировать по α на отрезке
. Следовательно, функцию I(α)
можно интегрировать по α на отрезке![]() :
:
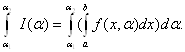
Выражение, стоящее справа, есть двукратный интеграл от функции f(x,α) по прямоугольнику, расположенному в плоскости Oxα. Можно изменить порядок интегрирования в этом интеграле:
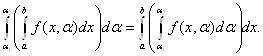
Эта формула показывает, что для интегрирования интеграла, зависящего от параметра α, достаточно проинтегрировать по параметру α подынтегральное выражение. Эта формула также бывает полезна при вычислении определенных интегралов.
Так как существует
конечный 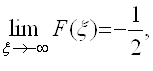 то
интеграл J существует и сходится (по определению), причем
то
интеграл J существует и сходится (по определению), причем ![]() .▲
.▲
Пример2.15 Вычислить
интеграл 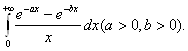
Неопределенный интеграл от подынтегральной функции не берется в элементарных функциях. Для его вычисления рассмотрим другой интеграл, который можно легко вычислить:
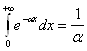 (α>0).
(α>0).
Интегрируя это равенство в пределах от α=a до α=b, получим
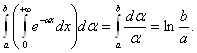
Меняя порядок интегрирования в первом интеграле, перепишем это равенство в следующем виде:
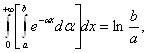
Откуда, вычисляя внутренний интеграл, получаем
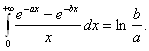 ■
■
Литература
1. Тер-Крикоров А.М., Курс математического анализа: Учебное пособие для вузов. -2-е изд, М.:Физмалит: Лаборатория Базовых Знаний, 2003.
2. Пискунов Н.С. Дифференциальное и интегральное исчисление: Учебное пособие для втузов.т.2,13-е изд. М.: Наука , Главная редакция физико-математической литературы, 1985.
3. Ильин В.А., Позняк Э.Г., Основы математического анализа. Части 1,2, М.: Наука, 1971, 1973.
4. Рудин У., Основы математического анализа, М.: Мир, 1966.
5. Зорич В.А., Математический анализ. Части 1,2, М.: Наука, 1981, 1984.
6. Фихтенгольц Г.М., Основы математического анализа. Тома 1.2, М.: Наука, 1968.
| Шпаргалки по математическому анализу для 1-го семестра в МАИ | |
|
Экзаменационная программа По курсу математического анализа для студентов групп 03-112 - 116. 1. Понятие n-мерного арифметического пространства Rn ... 49 Пусть ф-ция y=f(x) интегрируема на отр[a,b] тогда она интегрируема на отр[a,x] при a x b по св-ву опред F(x)= aтxf(t)dt, x [a,b] - которая называется интегралом с переменным ... Так как |aтb"f(x)dx| aтb" |f(x)| dx то после перехода к пределу при b' b для абсолютно сходящегося интеграла aтb f(x)dx получим |aтb f(x)dx| aтb |f(x)| dx {Глав зн не соб }Пусть ф ... |
Раздел: Рефераты по математике Тип: реферат |
| Ряды | |
|
Фун 2 числовых аргументов. Пусть имеется Е (х1;у1) - элементы принадлеж точке Е Сущ закон или правило по которому каж точке (xi;yi) ставится в соот-е ... Сущ закон или правило по которому каж точке (xi;yi) ставится в соот-е число Wi или любой точке (xi;yi) или паре чисел ставится в соот-е zi след-но zi=F(х;у), где Е-обл опред-я F(х ... Пусть область D ограничена линиями y=f1(x), y=f2(x), y=a, y=b (a<b, f1(x)<f2(x)). Пусть f(x,y) непрерывна в области D. 2) и 3) на любом отрезке [a,b], целиком принадлежащем интервалу сходимости(-R;R), ф-я F(x) является непрерывной, а следовательно степенной ряд можно почленно интегрировать и ... |
Раздел: Рефераты по математике Тип: шпаргалка |
| Теория вероятности и мат статистика | |
|
Киевский политехнический институт Кафедра КСОИУ Конспект лекций по курсу: "Теория вероятности и математическая статистика" Преподаватель: Студент II ... Согласно терминологии, если функция y=f(x) непрерывна на отрезке [a, b], то она ограничена. Пусть случайная величина Y является функцией f(x) от случайной величины X. Построим вероятностное пространство случайной величины Y. |
Раздел: Рефераты по математике Тип: реферат |
| Динамические системы в плоской области | |
|
... 1. Введение Мы будем рассматривать системы дифференциальных уравнений вида (I) где Р (х, у) и Q (х, у) - непрерывные функции, определенные в некоторой ... Так как в силу настоящей теоремы эти функции непрерывны по переменным х0, у0 и равномерно непрерывны относительно t на всяком замкнутом конечном промежутке значений t, то, очевидно ... Пусть какая-нибудь точка области G. В силу теоремы о существовании и единственности решения, если при значениях , P(), то существует единственное решение y=f(x), соответствующее ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| Построение систем распознавания образов | |
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ ДОНЕЦКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА О С Н О В Ы П О С Т Р О Е Н И Я С И С Т Е М Р А С П О З Н ... Но для равномерного распределения на интервале [a,b] имеем Это случается, например, когда интеграл от f(x) не выражается через элементарные функции или когда плотность f(x) задана только графически. |
Раздел: Рефераты по психологии Тип: реферат |