Научная работа: Оптические методы исследования процессов горения
Министерство общего и профессионального образования Российской Федерации
Чувашский государственный университет им. И.Н. Ульянова
ОПТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ ГОРЕНИЯ
А.Е. Давыдов
Чебоксары 2000 - 2007
1. ПРЯМОТЕНЕВОЙ МЕТОД
Прямотеневой метод позволяет приближенно определить вторую производную показателя преломления. Поэтому он нашел широкое применение при изучении явлений, связанных с резким изменением показателя преломления n, таких как ударные волны, зоны горения предварительно перемешанной горючей смеси, контроля оптических стекол.
I. Схема теневого метода
Один из наиболее простых вариантов установки для теневого метода приведен на рис. 1.1.
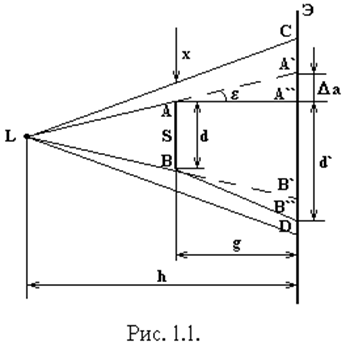
Здесь L - точечный источник света, Э - экран. Между ними помещается исследуемая неоднородность S. Свет от источника L при прохождении через шлиру отклоняется.
Пусть световой луч LA испытывает при прохождении через оптическую неоднородность отклонение на угол e (рис. 1.1). Вследствие этого он попадает не в точку А`, а в точку А``, которая удалена от А` на расстояние Dа=g×tge. Но так как угол e мал (а только такие случаи и имеет смысл исследовать теневым методом), то tge@e, и поэтому
Dа=e×g, (1.1)
где g - расстояние от оптической неоднородности до экрана.
Смещение точки падения луча на экране вызывает изменение освещенности, которое и указывает на наличие неоднородности на пути лучей. Относительное изменение освещенности экрана, то есть чувствительность теневого метода, пропорциональна отношению Dа/d`, где Dа - смещение точки падения луча на экране, d` - размер теневого изображения неоднородности.
Выясним, как зависит это отношение от параметров теневой установки. Из рис. 1.1 имеем:
![]() или
или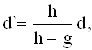 (1.2)
(1.2)
где d - размер неоднородности.
Поэтому
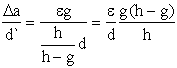 . (1.3)
. (1.3)
Отношение e/d зависит только от характера и размера неоднородности, и поэтому мы его можем считать заданной величиной.
Обозначим в (1.3) g/h через x. Тогда
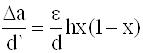 . (1.4)
. (1.4)
Функция f(x)=x(1-x) имеет максимум при x=0.5, то есть чувствительность максимальна при g/h=0.5 или при g=h/2.
Следовательно, для увеличения чувствительности теневого метода необходимо:
а) увеличить расстояние h от источника света до экрана насколько позволяет помещение;
б) помещать оптическую неоднородность приблизительно в середине между источником света и экраном Э.
Однако качество теневой картины на экране определяется не только указанным отношением Da/d`, но и другими факторами, например, не резкостью, вызванной дифракцией света на краю неоднородности, не резкостью, обусловленной конечными размерами источника света и необходимостью установки больших габаритов.
Исходя из вышеизложенного следует, что исследование фазовых объектов прямотеневым методом крайне затруднительно, поэтому для исследования оптических неоднородностей в данной работе используется обращенный теневой метод.
II. Обращенный теневой метод
Рассмотрим его оптическую схему, приведенную на рис. 1.2.
В качестве источников света в обращенном теневом методе обычно используются источники света с высокой яркостью. Эти источники можно использовать непосредственно сразу или для получения большой резкости теневой картины получить вначале с помощью конденсора промежуточное изображение на точечной диафрагме.
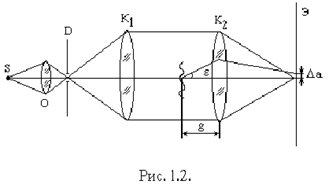
Свет от источника S проходит через конденсорную линзу О, диафрагму D и между линзами K1 и K2 образуется параллельный пучок. Неоднородность можно помещать в сходящемся, расходящемся и в параллельных пучках. Чувствительность метода может быть выражена формулой
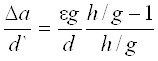 (1.5)
(1.5)
Из формулы (1.5) следует, что чувствительность, то есть отношение Da/d` теоретически может расти до бесконечности, если сделать сколь угодно малой величину теневого изображения оптической неоднородности на экране при постоянном значении Da. Если сохранить g постоянным и увеличивать отношение h/q, то чувствительность возрастает от 0 для h=g до значения eg/d при h®¥. h®¥ означает, что оптическая неоднородность просвечивается параллельным пучком света. Поэтому изображение ее равно размерам самой неоднородности. Если же оптическую неоднородность просвечивать сходящимся пучком света, оставляя постоянным g, то изображение шлиры будет меньше самой неоднородности. Так как при этом Da остается постоянным, то чувствительность существенно увеличивается. Но для получения сходящегося пучка лучей необходимо оптическое оборудование, так что основное преимущество теневого метода теряется.
В заключении отметим основные преимущества и недостатки теневого метода.
Основным преимуществом теневого метода является чрезвычайная простота установки, которая не требует почти никакого оптического оборудования, и возможность исследования объектов, имеющих значительные размеры.
Недостатком теневого метода является невозможность проведения точных количественных исследований структуры оптической неоднородности.
2. МЕТОД ТЕПЛЕРА
Метод исследования оптических неоднородностей, основанный на измерении угловых отклонений света e ~ grad n называется методом Теплера или шлирен-методом. Оптические установки, предназначенные для работы методом Теплера, называются приборами Теплера. Они встречаются в самых разнообразных вариантах в зависимости от их назначения.
I. Принципиальная схема прибора Теплера
Принципиальная схема прибора Теплера приведена на рис. 2.1.
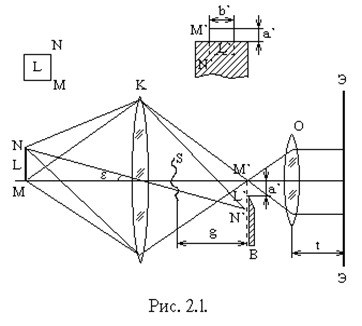
Источник света L представляет собой равномерно ярко светящуюся площадку MN, ограниченную по линии М прямолинейным краем. В верхней части рис. 2.1 слева приведен вид источника света L по направлению оптической оси. Длиннофокусный объектив К, исправленный на сферическую и хроматическую аберрации, создает в плоскости М`N` изображение источника L`. Диаметр объектива К должен быть больше размеров исследуемой неоднородности, которая помещается на пути света между объективом К и плоскостью М`N`. Острый край ножа Фуко должен располагаться строго параллельно прямолинейному краю изображения источника света. В верхней части рис. 2.1 справа приведено относительное расположение диафрагмы В и изображения источника света L`. Ширина незакрытой части изображения источника света обозначена через а`. Объектив О дает изображение объектов, находящихся в плоскости исследуемой шлиры S, на экране Э. Соответствующим подбором объектива О можно в известных пределах изменять размер изображения объектов на экране Э и выбрать подходящую для каждого случая освещенность. Обозначения расстояний между различными деталями установки приведено на рис. 2.1.
При отсутствии на пути света шлиры S и если нож Фуко не задерживает лучи в плоскости М`N`, экран Э будет освещен равномерно во всех точках. Освещенность экрана в этом случае обозначим через Е. Если ножом Фуко, перемещая его перпендикулярно оптической оси, задержать часть лучей, падающих на экран, то при отсутствии шлиры равномерность освещения экрана не нарушится, но величина освещенности, пропорциональная а`, уменьшится и станет равной Е`.
При наличии шлиры часть лучей света отклонится на некоторый угол e и вызовет смещение изображения источника света относительно начального изображения, создаваемого не отклоненными лучами на Dа`. На эту же величину оно будет смещено и относительно острого края ножа. Поэтому соответствующие места изображения шлиры получат больше или меньше света в зависимости от того, в какую сторону происходит смещение: если вверх, то освещенность будет больше, если вниз, то меньше, чем освещенность свободного поля при данном положении острого края ножа.
В отличие от теневого метода в шлирен-методе более освещенные и менее освещенные по сравнению со свободным полем части изображения неоднородности соответствуют тем местам шлиры, где происходит отклонение света, но только отклонения имеют противоположные направления.
Так как изменение освещенности экрана DЕ пропорционально смещению изображения источника света Dа`, а последнее однозначно зависит от угла отклонения света e, то по изменению освещенности точки на экране можно определить углы отклонения и, следовательно, grad n в соответствующей точке неоднородности.
Чувствительность метода Теплера
Наличие неоднородности на пути лучей в приборе Теплера выявляется по изменению освещенности экрана, что можно регистрировать, например, фотоэлементом. В этом случае под чувствительностью метода Теплера следует понимать наименьшее абсолютное изменение освещенности (соответствующее наименьшему углу отклонения), которое можно еще зафиксировать с достаточной точностью.
Если же экран наблюдается визуально или фотографируется, то под чувствительностью метода Теплера понимается относительное изменение освещенности экрана a=DЕ/Е, которое еще можно хорошо различить. Изменение освещенности экрана происходит вследствие смещения изображения источника света, создаваемого отклоненными лучами, относительно острого края диафрагмы. Это смещение Dа` пропорционально углу отклонения света в шлире:
Dа`=e×g,
где g - расстояние от неоднородности до плоскости изображения источника света. Тогда на основании выражения для вычисления освещенности экрана, полученного Г.Шардиным
Е+DЕ=hВb`(a`+Dа`)/t2, (2.1)
где h - коэффициент, учитывающий потери в стекле объектива К на отражение и поглощение,
В - яркость источника света,
t - расстояние от главной плоскости объектива О до плоскости экрана Э, можно написать
Е+DЕ=hВb`(a`+Dа`)/t2= hВb`(a`+em g)/t2, (2.2)
где em - наименьший угол отклонения, который можно еще зафиксировать. Разделим почленно полученное выражение на (2.1):

откуда a=em g/a`. (2.3)
Полученное соотношение показывает, что чувствительность метода Теплера прямопропорциональна расстоянию g между диафрагмой и оптической неоднородностью и обратно пропорциональна степени перекрытия диафрагмой изображения источника света.
Теоретически из (2.3) следует, что чувствительность стремится к бесконечности при а`®0. Практически этому мешают дифракционные явления, которые становятся тем заметнее, чем уже делается пропускаемый диафрагмой пучок света. Кроме того, для хорошей различимости изображения необходима известная освещенность поля изображения на экране. Исходя из уравнения (2.1) можно было бы, изменяя ширину изображения щели b`, поддерживать определенную освещенность Е при любом расстоянии а`, однако по техническим причинам желательное увеличение ширины изображения источника света невозможно.
II. Юстировка и настройка прибора Теплера.
Установка диафрагмы
Диафрагма, которая устанавливается в плоскости изображения источника света и служит для перекрытия части лучей, приходящих на экран, играет существенную роль в методе Теплера и от правильной ее установки зависит точность количественных исследований.
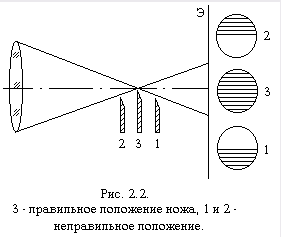
Рассмотрим приемы определения правильного положения диафрагмы с одним острым прямолинейным краем (ножа Фуко) при применении в качестве источника света ярко освещенного прямоугольника. Наиболее универсальным является следующий способ. После определения приблизительного положения диафрагмы начинают вдвигать (с помощью микрометрического винта) нож перпендикулярно оптической оси с одной какой-нибудь стороны (рис. 2.2). Вероятно, поле на экране при этом начинает темнеть с одной стороны. Если на экране тень будет надвигаться с той же стороны, что и нож, то это значит, что диафрагма находится между плоскостью изображения источника света и экраном (положение 1 на рис. 2.2). Поэтому диафрагму следует поставить дальше от экрана. Если в новом положении диафрагмы, при ее вдвигании тень будет надвигаться в направлении, противоположном движению диафрагмы, то это означает, что диафрагма находится между плоскостью изображения источника света и объективом, следовательно, ее надо поставить подальше от объектива. Повторяя далее эти операции, можно установить диафрагму точно в плоскости изображения источника света. В этом случае, при диафрагмировании изображения источника света, поле на экране будет темнеть равномерно во всех точках. Возможные при этом неравномерности в освещенности поля на экране могут быть вызваны только недостатками объектива. Можно для правильной установки ножа рекомендовать другой способ. Вблизи изображения источника света (между ним и экраном) устанавливают лупу, которая проектирует увеличенное изображение источника света и края диафрагмы на какой-нибудь экран. Перемещая лупу вдоль оптической оси системы, добиваются резкого изображения на экране источника света. Закрывая далее ножом приблизительно половину изображения источника света и передвигая нож вдоль оптической оси, добиваются резкого изображения острого края диафрагмы (ножа) на экране, что означает, что диафрагма находится в плоскости изображения источника света. Так как изображения прямолинейного края диафрагмы и источника света на экране получаются увеличенными, то, наблюдая взаимное расположение края ножа и изображения источника света на экране и, поворачивая нож в его плоскости вокруг оптической оси, легко установить параллельность прямолинейного края диафрагмы и прямолинейного края изображения источника света. Так же, как и при первом способе, необходимо, чтобы на пути лучей не было оптических неоднородностей и посторонних предметов, так как это ведет к размытости краев изображения источника света. Описанный прием удобен тем, что изображение на экране можно получить значительно увеличенным и одновременно контролировать наличие зазубрин и пылинок на прямолинейном краю диафрагмы и на краях источника света и равномерную освещенность поверхности источника света.
Немалую роль для точности количественных исследований играет правильный выбор расстояния а` - расстояния от прямолинейного края ножа до края изображения источника света. Если ожидаются большие отклонения света при прохождении через неоднородность, то расстояние а` нужно выбирать большим, если же предполагаются малые отклонения, то - малым. Это легко определить предварительным визуальным наблюдением картины в плоскости изображения источника света.
Определение правильного положения экрана
Изображение на экране Э предметов и оптических неоднородностей, находящихся в плоскости s, создается при помощи объектива О.
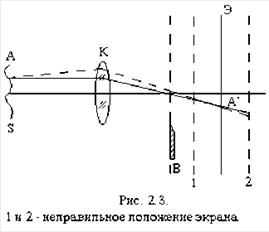
Чаще в качестве объектива О используется один из двух шлирен-объективов, когда оптическая неоднородность помещается на пути параллельных пучков света (рис. 2.3). В последнем случае плоскость расположения оптической неоднородности и плоскость экрана являются сопряженными относительно объектива К. При малых углах отклонения света в оптической неоднородности можно считать, что даже после ее введения изображение плоскости s на экране Э остается идентичным изображению, проектируемому невозмущенным пучком света. На рис. 2.3 приведен ход луча, проходящего через точку А при отсутствии неоднородности (сплошная линия) и в случае наличия неоднородности, когда он получает малое отклонение (пунктирная линия). В обоих случаях луч попадает в одну и ту же точку экрана А`. Заметим, что сплошная и пунктирная линии пересекают плоскость изображения источника света, где находится нож, в разных точках, т.е. каждый луч удален от края ножа на различные расстояния а`. Если же экран расположен неправильно (положения экрана 1 и 2, проведены пунктиром), то лучи, отмеченные сплошной линией и пунктирной линией, не попадают в одну и ту же точку экрана, что создает теневой эффект от шлиры. Следовательно, для правильной установки экрана необходимо определить такое положение экрана, в котором при убранной диафрагме оптическая неоднородность не видна. Конечно, сильные оптические неоднородности могут быть несколько заметны и при не правильном положении экрана, например, плоский фронт кинетического пламени, или когда оптическая неоднородность имеет значительную глубину.
Прибор интерференционно-теневой ИАБ-458
Прибор интерференционно-теневой ИАБ-458 предназначен для качественных и количественных исследований теневым методом неоднородностей оптически прозрачных сред. В приборе реализуются следующие методы исследования: светящейся точки, щели и ножа, щели и нити, сдвиговой интерферометрии и голографии.
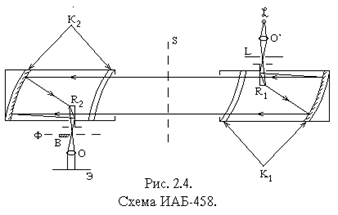
На рис. 2.4 приведена принципиальная схема прибора Теплера ИАБ-458. Он состоит из двух оптических систем: коллиматорной, которая создает параллельный пучок света для просвечивания исследуемой неоднородности, и наблюдательной, которая служит для наблюдения и фотографирования теневой картины.
Коллиматорная часть состоит из зеркально-менискового объектива К1 диаметром 230 мм и фокусным расстоянием 1917 мм, плоского зеркала R1 для изменения направления лучей, закрепленного на одной каретке со щелью L. Последняя устанавливается в фокусе объектива К1. На каретке имеются механизмы поворота и изменения ширины щели.
Наблюдательная часть состоит из точно такого же зеркально-менискового объектива К2, что и в коллиматорной части, плоского зеркала R2 для изменения направления лучей, закрепленного на каретке с ножом В. Последний устанавливается в фокальной плоскости ФФ зеркально-менискового объектива К2. Объектив О может перемещаться вдоль оптической оси и служит для получения резкого изображения шлир и других объектов, находящихся в плоскости ss, на экране Э. На каретке с ножом установлены механизмы перемещения и поворота ножа.
Изменение ширины щели и перемещение ножа в фокальной плоскости объектива К1 производится микрометрическими винтами с точностью до сотых долей миллиметра. Высоту щели можно менять с помощью вставной диафрагмы. Кроме того, имеется вставная диафрагма с отверстиями различных диаметров, которой пользуются при необходимости иметь источник света в форме светящегося круга. В качестве диафрагмы, кроме ножа, можно пользоваться "нитями" различных диаметров.
К каретке наблюдательной системы прикреплен откидной кронштейн, выполненный в виде самостоятельной части. На нем укреплены объектив О, фотозатвор "Темп" и приспособления, позволяющие одновременно наблюдать и фотографировать теневую картину.
Ход лучей в приборе ИАБ-458 показан на рис. 2.4. Щель L с помощью конденсора О` равномерно ярко освещается лампочкой накаливания (12 вольт, 50 ватт) или одной из ртутных ламп ДРШ 250-3 или ДКсШ-200. Свет через щель проходит на зеркало R1 и, отражаясь, падает на зеркало объектива K1 и после второго отражения идет к мениску объектива К1. Так как щель L находится в фокусе объектива К1, то после мениска получается параллельный пучок света. Далее свет проходит через мениск и отражается от зеркала объектива К2 и падает на зеркало R2. После отражения от него в фокальной плоскости объектива К2 создается изображение щели - изображение источника света. Так как зеркально - менисковые объективы К1 и К2 совершенно идентичны, то размеры изображения щели равны размерам самой щели.
К прибору прилагается ряд принадлежностей, из которых следует отметить: окуляры (увеличение в 2.5 и в 5 раз), фотоприставки (ФЭД и рамка от "фотокора"), лупа для проектирования изображения источника света на экран, блок питания для лампочки накаливания и для ДРШ 250-3 и ДКсШ-200, футляры для установки и удержания их, набор призм Волластона, набор "нитей", голографическая приставка РП-460.
III. Методы измерения отклонения света на приборе Теплера
При исследовании относительно грубых шлир удобно пользоваться методами измерения e, не требующими кропотливого процесса фотометрирования. К таким методам относятся метод щели и ножа, метод щели и нити и метод щели и решетки. При применении этих методов в качестве источника света в приборе Теплера используется равномерно ярко освещенная щель.
Как показали исследования Д.Д. Максутова, щель имеет ряд преимуществ перед другими формами источников света и, в частности перед точкой:
1. При той же ширине, что и диаметр точки, и при той же степени перекрытия ее изображения диафрагмой, щель посылает на экран значительно больше света.
2. Значительно повышается чувствительность метода.
3. Дифракционный интерферометр на базе ТЕНЕВОГО прибора ТЕПЛЕРА ИАБ-458 (ИАБ-451)
Среди различных оптических интерферометров широкое применение находит интерферометр с дифракционной решеткой. Применение интерферометров с дифракционной решеткой объясняется тем, что использование дифракционных решеток является удобным способом создания когерентных пучков света.
Вторым положительным качеством интерферометров рассматриваемого типа является то, что при использовании решеток из натянутых нитей или отражательных решеток интерферометрические исследования можно проводить в ультрафиолетовом, инфракрасном и даже СВЧ диапазонах электромагнитных колебаний. Эта особенность является очень важной, так как позволяет применять их для изучения объектов новых классов, имеющих большое практическое значение, например, лазерных систем на углекислом газе, дающих излучение с длиной волны 10.6 мкм.
Наконец, интерферометры с дифракционной решеткой просты и их легко можно, использовать совместно с приборами других типов, например, теневыми приборами.
I. Основы теории интерферометра с дифракционной решеткой
1.1 Основные положения
Свойства интерферометров с дифракционной решеткой в первую очередь определяются характеристиками решетки. Под решеткой обычно понимают периодическую структуру, состоящую из системы прозрачных или отражающих штрихов, вносящих амплитудные, фазовые или в общем случае амплитудно-фазовые изменения в проходящую через них световую волну. Как правило, штрихи прямолинейны и параллельны между собой, однако находят применение интерферометры, в которых решетка представляет собой систему концентрических окружностей.
Основной характеристикой решетки является ее период d-расстояние между аналогичными линиями штрихов, измеренное в направлении, перпендикулярном штрихам. Иногда в качестве характеристики используют частоту - величину, обратную периоду. Второй характеристикой является форма штриха, определяющая зависимость величины амплитудно-фазовых изменений, вносимых решеткой в световой поток, от координаты, перпендикулярной штрихам. Как правило, используют решетки с простой формой штриха - трапецеидальной, синусоидальной, прямоугольной, треугольной.
Период дифракционных решеток изменяется в широких пределах от 10 до 104 штрихов на 1 мм, но для целей интерферометрии чаще всего используют решетки с малой частотой штриха - от 10 до 102 штрихов на 1 мм.
Как известно, после взаимодействия света с дифракционной решеткой пучок параллельных световых лучей разбивается на серию отдельных пучков - дифракционных максимумов. Направление распространения этих пучков определяется из соотношения
sina - sinb = Nl/d, (3.1)
где a и b - соответственно углы, составляемые направлениями распространения идущего от решетки и падающих на решетку световых потоков и нормалью к ней; N - порядковый номер дифракционного максимума, N=0, ±1, ±2, ...; l - длина световой волны.
Если первоначальный пучок света падает нормально к решетке, то вместо равенства (3.1) имеем
sina = Nl/d. (3.2)
При сравнительно грубых решетках, когда углы дифракции малы, равенства (3.1) и (3.2) принимают вид
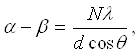 (3.3)
(3.3)
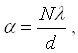 (3.4)
(3.4)
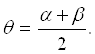
Так как для большинства схем интерферометров N = 0; 1 или 2, а частота штрихов не превышает 100 штрихов на 1 мм, то почти всегда следует пользоваться равенствами (3.3) и (3.4).
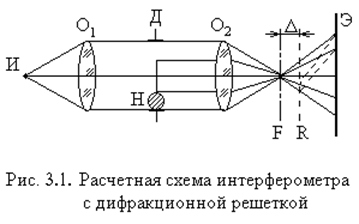
Одна из распространенных оптических схем, на примере которой удобно описать явления, происходящие в интерферометрах с дифракционной решеткой, дана на рис. 3.1.
Источник света И находится в фокальной плоскости основного объектива О1 осветительной части прибора. Часто вместо источника, устанавливаемого непосредственно в фокальной плоскости, применяют систему конденсорных объективов и в качестве источника используют промежуточное изображение светящегося тела. Это удобно, так как промежуточное изображение легко ограничить диафрагмами нужной формы и тем самым удовлетворить требованиям, предъявляемым к источнику света с точки зрения необходимости ограничения его размеров в одном или двух направлениях. Чаще всего такими диафрагмами являются щель или осветительная дифракционная решетка. Из объектива О1 выходит коллимированный пучок света, который проходит через исследуемую неоднородность Н. В плоскости предметов интерферометра, где расположена Н, устанавливают также и диафрагму Д, выделяющую в поле прибора рабочий участок и поле волны сравнения. В практических условиях иногда невозможно поставить Д в плоскость предметов. В этих случаях отступают от идеальной схемы и помещают диафрагму поля предметов Д между неоднородностью и объективом О2. Так как в пространстве О1 и О2 световой пучок коллимирован, то, как правило, такое отступление не приводит к существенному изменению интерференционной картины. За плоскостью предметов устанавливают О2 - основной объектив приемной части прибора, размер которого выбирают так, чтобы его оправа не ограничивалась ни одной из интерферирующих волн. Вблизи от F - второй фокальной плоскости объектива О2 установлена дифракционная решетка R. За решеткой располагается плоскость экрана Э, который устанавливают в том месте, где находится изображение неоднородности Н. При использовании результатов экспериментов необходимо умножить все линейные размеры изображения на масштаб.
На экране наблюдается серия изображений, не закрытых непрозрачными зонами диафрагмы Д участок плоскости предметов, каждое из которых оборудовано светом одного из дифракционных максимумов. Эти изображения сдвинуты относительно нулевого, не сдвинутого изображения, на величину
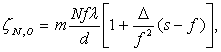 (3.5)
(3.5)
где m - масштаб изображения; f — фокусное расстояние объектива О2; s - расстояние от плоскости предметов до первой главной плоскости объектива О2.
Расстояние между изображениями различных порядков
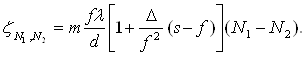 (3.6)
(3.6)
Для того чтобы рабочая волна и волна сравнения полностью накладывались одна на другую, необходимо, чтобы величина сдвига равнялась расстоянию b между изображениями отверстий диафрагмы. Это достигается при
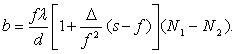 (3.7)
(3.7)
Как правило, величины s и f одного порядка, а D значительно меньше, чем каждая из них. Это позволяет пренебречь вторым членом в квадратных скобках выражений (3.5) - (3.7) и записать их в упрощенном виде:
![]()
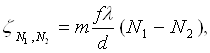
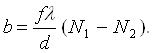
Практически, если в качестве основы прибора используется теневой прибор ИАБ-458, имеющий световой диаметр основных объективов 230 мм и f=1918 мм, то при l=5,25.10-4 мм и интерференции +1 и -1 максимумов для b=60 мм необходимо иметь решетку с частотой 30 штрихов на 1 мм. При интерференции нулевого и первого максимумов можно для рабочего участка использовать половину поля прибора, и для b=100 мм необходимо взять решетку с частотой 100 штрихов на 1 мм.
1.2 Схема интерферометра
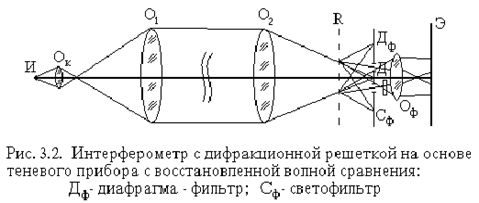
Интерферометр с дифракционной решеткой на основе теневого прибора с восстановлением волной сравнения приведен на рис. 3.2.
II. Юстировка и настройка интерферометра
До ввода в действие прибор должен быть отъюстирован. Сборка и юстировка большинства основных деталей интерферометра существенно не отличаются от аналогичных операций для других оптических приборов.
Однако существует несколько операций юстировки, специфичных только для интерферометров с дифракционной решеткой. Это установка диафрагм, выделяющих рабочее поле и поле сравнения, и особенно юстировка дифракционных решеток в осветительной и приемной частях прибора.
Установка диафрагм довольно проста. Их размер и расположение определяются по формулам. Контроль точности установки ведут визуально по совмещению интерферирующих полей. Допустимая погрешность установки обычно велика. Необходимо только, чтобы несовпадение полей было много меньше размера каждого из полей, а это обычно достигается при погрешности установки, примерно равной 0.5-1 мм.
Установка и юстировка дифракционных решеток более сложна, поэтому опишем ее подробно.
Дифракционная решетка приемной части прибора должна быть перпендикулярна оптической оси. Кроме этого необходимо знать положение решетки относительно плоскости изображения осветительной диафрагмы, которая, как правило, совпадает с фокальной плоскостью основного объектива приемной части прибора. Решетку в фокальной плоскости прибора устанавливают одним из двух способов.
Первый способ - автоколлимационный. У основного объектива устанавливают плоское зеркало и через микроскоп одновременно наблюдают дифракционную решетку и ее изображение, образованное после двукратного прохождения через основной объектив и отражения от плоского зеркала. Решетку передвигают вдоль оптической оси до тех пор, пока она и ее изображение не будут одновременно резко видны. Перпендикулярность решетки оптической оси устанавливают и проверяют путем наблюдения периферийных участков решетки, где решетка и ее изображение должны быть одновременно так же резко видны, как и на оптической оси. Этот метод позволяет совмещать решетку с фокальной плоскостью с погрешностью ±0.1 мм для систем, основанных на использовании прибора ИАБ-458.
Второй способ установки решетки в фокусе перпендикулярно оптической оси основан на наблюдении интерференционной картины. При выведенной из фокуса решетке поле освещено неравномерно. Передвигая решетку вдоль оси, добиваются равномерности освещенности поля. При этом считают, что решетка находится в фокусе.
Специфичным этапом юстировки является установка диафрагмы осветительной части прибора, которая ограничивает промежуточное изображение источника света. Если такой диафрагмой служит щель, то она должна быть расположена перпендикулярно оптической оси и параллельно штрихам осветительной решетки.
Не параллельность штрихов приемной и осветительной решеток приводит к увеличению эффективной ширины источника света в направлении, перпендикулярном штрихам решетки, и к снижению контраста интерференционной картины.
Параллельность штрихов решетки обеспечивают одним из двух способов. При первом способе после грубой установки решеток, которая определяет направление интерферирующих полос, поворачивают одну из решеток и наблюдают интерференционную картину в плоскости изображений. Штрихи считают параллельными при таком положении решетки, при котором контраст максимален. Способ используют при настройке на конечную ширину полос, и он имеет то преимущество, что при настройке добиваются максимальной величины наиболее важного при измерениях параметра картины- контраста.
Этим способом нельзя устанавливать решетки параллельно при настройке на бесконечную ширину полос, так как при сдвиге решетки в плоскости изображения источника света юстировка может нарушиться. Поэтому часто приемную решетку устанавливают, совмещая ее с изображением осветительной решетки. Изображение наблюдают через микроскоп или на экране. Грубую настройку можно осуществлять по муаровой картине пересекающихся штрихов осветительной и приемной решеток. Для дальнейшего уточнения положения решеток необходимы наблюдения приемной решетки и изображения осветительной решетки через микроскоп.
Из-за неточности изготовления основных объективов их фокусные расстояния могут иметь некоторый разброс. Поэтому даже при точной установке решеток в фокус периоды изображений осветительной и приемной решеток могут иметь некоторый разброс. Это приводит к ухудшению контраста картины. Для устранения действия этого фактора осветительную решетку сдвигают относительно фокуса объектива приемной части и тем самым меняют масштаб ее изображения. При этом решетку осветительной части каждый раз устанавливают в плоскость изображения осветительной решетки. Наблюдая в микроскоп за соответствием периодов решетки и изображения, добиваются того, чтобы они были равными.
Опыт показывает, что с помощью описанных методик можно добиваться того, чтобы характеристики реального прибора незначительно отличались от идеального. При этом контраст интерференционных полос получается практически равным теоретически рассчитанному.
4. ПОЛЯРИЗАЦИОННЫЙ ИНТЕРФЕРОМЕТР СДВИГА НА БАЗЕ ПРИБОРА ТЕПЛЕРА ИАБ-458 (ИАБ-451)
В поляризационных интерферометрах для получения смещенных волновых фронтов (световых пучков) используются поляризационные призмы - преимущественно призмы Волластона, иногда - полярископ Савара. Для поляризации света и получения интерферограммы применяются поляроиды. Поляризационные интерферометры работают по схеме компенсации разности хода, что дает возможность использовать широкий источник света и обеспечивать получение яркой интерферограммы. То есть в этих интерферометрах та часть разности хода, которая зависит от положения светящейся точки источника, компенсируется путем пропускания света через вторую призму.
Поляризационные интерферометры сдвига очень просты в юстировке и регулировках.
I. Схема поляризационного интерферометра сдвига на базе прибора ИАБ-458
Поляризационный интерферометр может быть получен на основе двухобъективного теневого прибора типа ИАБ-458, если в последнем щель и нож заменить призмами Волластона W1 и W2, установленными перпендикулярно к оптической оси прибора (рис 4.1.). Для получения поляризованного света и наблюдения интерференционной картины перед первой призмой и за второй необходимо соответствующим образом установить поляроиды Р1 и Р2.
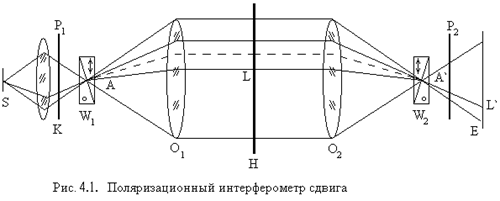
Перемещением призмы в приемной части вдоль оптической оси относительно фокуса возможна настройка на интерференционные полосы различной ширины. Если призмы Волластона стоят так, что фокусы приходятся на преломляющие грани, то интерферометр настроен на полосы бесконечной ширины.
Конденсор К образует изображение источника света S в фокальной плоскости первого главного объектива О1. Второй раз изображение источника, перевернутое по отношению к первому, образуется в фокальной плоскости второго объектива О2. Исследуемый объект Н помещается между линзами О1 и О2 в параллельном пучке. Средние плоскости призм параллельны друг другу. Плоскость поляризации поляризатора Р1 составляет угол 450 с оптическими осями призмы. Анализатор Р2 параллелен или скрещен с поляризатором.
На рис 4.1. изображен ход одной пары интерферирующих лучей в случае, когда призмы находятся "в фокусах" главных объективов, т.е. по отношению к оптической системе линз О1 и О2 плоскости локализации изохроматических полос совпадают со взаимосопряженными плоскостями. Падающий луч выходит из внеосевой точки источника. В призме W1 он разделяется на лучи 1 и 2. Каждый из лучей 1 и 2, пересекая призму, отклоняется в противоположных направлениях на угол q/2.
Продолжение падающего луча пересекает исследуемый объект в точке L. После прохождения главных объективов лучи 1 и 2 направляются на вторую призму. Их мнимые продолжения пересекаются в точке А` - изображения точки А в первой призме. В призме W2 лучи 1 и 2 снова отклоняются на угол q/2 и соединяются в один луч. При этом во второй призме лучи 1 и 2 должны отклоняться в том же направлении, что и в первой призме.
Оптические пути лучей в воздухе вычислим в приближении, что толщина призмы 2d мала по сравнению с фокусным расстоянием F главных объективов. При вычислении оптических длин лучей в призмах будем пренебрегать наклоном лучей к оси прибора.
Начальная разность хода D между лучами 1 и 2 после пересечения ими второй призмы равна сумме разности de оптических длин в воздухе при распространении света от точки А до точки А` и сумме разностей D1 и D2 оптических длин в призмах. Согласно свойству идеальной оптической системы de=0. Поэтому для получения D достаточно знать Dw=D1+D2.
Призмы вносят разность хода
D1=q1(x1-x1) и D2q2(x2-x2). (4.1)
В компенсационных интерферометрах призмы по отношению одна к другой располагаются таким образом, чтобы осуществлялась компенсация разности хода, зависящей от положения светящейся точки, т.е. чтобы q1x1 и q2x2 имели противоположные знаки. Этому условию удовлетворяют два различных положения второй призмы. В первом положении призмы обращены друг к другу с одинаковыми оптическими осями, но преломляющие углы имеют противоположный знак. Во втором положении призмы обращены друг к другу разными оптическими осями, а преломляющие углы имеют одинаковый знак.
Когда фокусные расстояния главных объективов равны, компенсация разности хода для различных точек источника света происходит при выполнении условия
q1x1 + q2x2 = 0.
Обычно увеличение оптической системы О1-О2 равно единице, поэтому /х1/=/х2/. Следовательно, призмы должны иметь одинаковый преломляющий угол. В этих условиях
D=qx, (4.2)
где x=x1+x2 определяют взаимное расположение средних плоскостей двух призм. Когда призмы находятся в "фокусах" главных объективов, то есть во взаимосопряженных плоскостях, начальная разность хода по всему полю интерференции есть постоянная величина. С немонохроматическим источником на экране наблюдается один цвет - интерферометр настроен на бесконечную полосу.
Когда реализовано условие компенсации разности хода, начальная разность хода не зависит от положения светящейся точки источника света и в интерферометре можно использовать широкий источник света.
При смещении призмы на z1 вдоль оси пучка абсцисса точки падения данного луча на призму изменяется на
Dх`= z1х/F,
где х - абсцисса луча в плоскости главного объектива, или практически то же самое в области исследуемого объекта.
С призмами, не находящимися во взаимосопряженных плоскостях, с учетом формул (4.1) и (4.2), начальная разность хода в поле интерференции определяется соотношением:
D=q(x+zx/F), (4.3)
где z=z2-z1 есть взаимная расфокусировка призм.
Следовательно, в этом случае поле интерференции состоит из системы прямолинейных полос, перпендикулярных направлению сдвига. Ширина полос равна
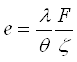 . (4.4)
. (4.4)
I. Сборка и настройка поляризационного интерферометра сдвига на базе теневого прибора ИАБ-458
При работе в режиме интерферометра сдвига в коллиматоре необходимо снять механизм щели и на его место установить узел с призмой Волластона с поляроидом.
В приемной части вместо ножа Фуко установить призму Волластона таким образом, чтобы была нужная ориентация сдвига и нужная настройка интерференционной картины.
Затем добиться резкости изображения объекта исследования. Если надо, установить фотокамеру и фотографировать. Но прежде, необходимо проделать следующие этапы юстировки.
1. Отъюстировать каждый светоделительный узел в отдельности, т.е. определенным образом установить поляроиды относительно призмы.
При правильной юстировке интенсивности интерферирующих пучков должны быть равны и, кроме того, максимальны. Для этого достаточно установить поляроид и призму относительно друг друга на глаз, разглядывая сквозь них отдаленный предмет (лучше всего в виде креста - например, оконный переплет на противоположной стороне улицы) и, поворачивая поляроид до тех пор, пока оба изображения предмета не окажутся одинаково яркими. Рекомендуется при этом держать узел поляроидом к предмету.
2. Дальше правильно ориентировать светоделительные узлы относительно друг друга.
Для этого заметить направление двоения каждого узла. Затем сложить оба узла вместе, призмами внутрь, таким образом, чтобы эти направления совпадали, и снова посмотреть на предмет. Возможны два случая:
а) предмет виден нераздвоенным
б) предмет раздваивается вдвое сильнее
Случаи а) и б) переводятся один в другой поворотом одного из узлов на 1800. Правильной ориентации отвечает второй случай.
В таком положении светоделительные узлы устанавливаются в прибор.
3. После того, как светоделительные узлы выставлены и ориентированы относительно друг друга, приступить к окончательной юстировке интерферометра.
Определить правильное начальное положение светоделительных узлов по отношению к фокальным плоскостям коллиматорного и приемного объективов. (Начальным положениям обоих узлов будем называть такое, при котором в поле интерференции видна бесконечно широкая полоса).
Для этого в фокальной плоскости коллиматора установить щель. Между щелью и источником света поместить поляроид. Установить в прибор приемный светоделительный узел так, чтобы направление двоения его было перпендикулярно щели. Поляроид, стоящий перед щелью, повернуть так, чтобы два изображения рабочего поля казались одинаково яркими. Сузить щель до ширины не более 0.1 мм. Поворотами светоделительного узла добиться появления интерференционной картины. Подвижкой узла вдоль оптической оси установить его так, чтобы в плоскости наблюдения образовалась бесконечно широкая полоса. Затем сместить светоделительный узел перпендикулярно оптической оси в направлении сдвига до получения картины с насыщенной окраской, т.е. полосы приблизительно нулевого порядка.
4. Снять узел щели и установить в прибор, светоделительный узел осветительной части, ориентируя его по отношению к светоделительному узлу приемной части так, как сказано в пункте 2. Слегка разворачивая светоделительный узел осветительной части вокруг оптической оси, добиться появления интерференционной картины. Затем подвижкой этого же узла вновь установить в плоскости наблюдения бесконечно широкую полосу.
5. Светоделительный узел приемной части повернуть так, чтобы сдвиг имел требуемое направление (например, по оси модели или перпендикулярно ей). При этом наблюдать раздвоенное изображение модели либо должным образом ориентированного перекрестия.
6. Светоделительный узел осветительной части повернуть вновь, добиваясь появления интерференционной картины (бесконечно широкой полосы). Поперечной подвижкой приемного осветительного узла получить полосу нулевого порядка.
7. Выполнить заключительные операции - настройку прибора. Ввести светофильтр для монохроматизации излучения и настройте прибор на полосы необходимой ширины и требуемого знака клина интерференции. Это обеспечивается подвижкой светоделительных узлов от начального положения вдоль оптической оси. Их перемещают на одинаковые отрезки навстречу друг другу либо наоборот. Величиной подвижки задается ширина полос, направлением - знак клина интерференции.
8. Фокусировать фотоприставку на выбранную плоскость исследуемого объекта, рассматривать интерференционные полосы на изображении этой плоскости. Если контраст полос неудовлетворителен, то следует повысить его. Для этого светоделительные узлы переместить по оптической оси на равные отрезки в одном направлении и найти для них положение, обеспечивающее наибольший контраст.
9. Убрать светофильтр, и поперечной подвижкой приемного светоделительного узла привести нулевую полосу в требуемое положение.
Юстировка поляризационного интерферометра
Юстировка поляризационного интерферометра чрезвычайно проста и не требует специальных приборов и приспособлений. Ограничимся лишь краткими замечаниями. Юстировка интерферометра должна привести к тому, чтобы в данных условиях интерферограмма имела самые насыщенные цвета (с немонохроматическим источником) или максимальный контраст и самую высокую яркость. Для этого одна призма по отношению к другой должна быть ориентирована таким образом, чтобы происходила компенсация разности хода. Плоскость поляризации поляроидов должна составлять угол 45° с главными сечениями призм. При этом достаточно выставить призмы перпендикулярно к световому пучку простыми механическими средствами. Высокое качество юстировки обеспечивает методика, в которой основным является получение равенства освещенностей двух изображений какого-нибудь предмета, находящегося в рабочем поле интерферометра ("правило равных освещенностей"). По этой методике юстировка компенсационного интерферометра проводится в следующей последовательности:
а) Вторая (по ходу света) призма и первый поляризатор устанавливаются на свои места и, наблюдая удвоение изображения какого-нибудь предмета на пути света, выбирают нужное направление сдвига световых пучков. Затем поворотом поляризатора добиваются равенства освещенностей двух изображений. Это положение и будет соответствовать тому, что плоскость поляризации падающего света составляет 45° с оптическими осями призмы.
б) Ставят на место анализатор и снова получают равенство освещенностей двух изображений. Это, очевидно, произойдет тогда, когда поляроиды будут параллельны или скрещены.
в) Помещают на место первую призму. При вращении этой призмы равенство освещенностей получается в четырех различных положениях. Но компенсация разности хода может происходить только в одном из этих положений. Небольшими и медленными поворотами одной из призм в вертикальной плоскости вблизи положения равенства освещенностей находят интерференционную картину.
Как было показано выше, компенсация разности хода происходит независимо от того, какими поверхностями призмы обращены друг к другу, что на практике очень облегчает юстировку компенсационного интерферометра.
При сравнительно больших угловых сдвигах необходимо соблюдать еще такое условие. Когда юстировку интерферометра проводят с источником белого света, с самого начала призмы должны быть выставлены так, чтобы изображение источника света приходилось на их центральную часть. Только в этом случае начальная разность хода будет мало отличаться от нуля и можно сразу получить интерференционную картину. При настройке на один цвет для уменьшения влияния хроматизма и недостатков изготовления призмы их следует располагать как можно ближе к фокусам светового пучка. После получения интерференционной картины перемещениями призмы вдоль оси светового пучка интерферометр можно настроить на бесконечную полосу или на полосы.
При малых угловых сдвигах нет смысла говорить о месте локализации интерференционных полос: полосы четкие в любой плоскости области переналожения двух пучков. При больших сдвигах полосы локализованы в плоскости, проходящей через мнимые точки пересечения интерферирующих лучей в пространстве предметов. Плоскость локализации полос можно совместить с плоскостью исследуемого объекта изменением соотношения между смещениями z1 и z2.
Несколько слов об элементах конструкции поляризационного интерферометра сдвига по схеме компенсации. Когда интерферометр собирается в лабораторных условиях, то с целью упрощения его конструкции можно снабдить регулировочными винтами только вторую (по ходу луча) призму. При этом регулировочные винты должны обеспечивать смещение призмы перпендикулярно к оси светового пучка с точностью в несколько угловых минут. Для получения достаточно узких полос расфокусировка призмы должна достигать примерно 0.1 фокусного расстояния главных объектов.
5. АВТОКОмПЕНСАЦИОННЫЙ ИНТЕРФЕРОМЕТР сДВИГА
В автокомпенсационных интерферометрах свет пересекает исследуемый объект два и более раз. Такие интерферометры лучше приспособлены для исследования слабых оптических неоднородностей.
I. Интерферометр со сферическим зеркалом
Принципы действия автокомпенсационного интерферометра рассмотрим на примере установки со сферическим зеркалом М в качестве главного объектива (рис. 5.1). Призма Волластона W установлена вблизи центра кривизны сферического зеркала.
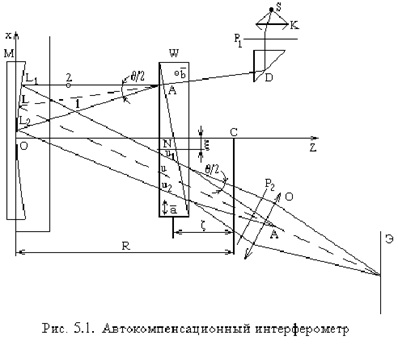
Световой
пучок, идущий от источника S поляризован под углом 45° к оптическим осям ![]() и
и ![]() призмы. K – конденсор, D – призма полного
внутреннего отражения, P1 и P2
– поляроиды. О – проектирующий объектив, Э – экран.
призмы. K – конденсор, D – призма полного
внутреннего отражения, P1 и P2
– поляроиды. О – проектирующий объектив, Э – экран.
Вычислим начальную разность хода. Рассмотрим общий случай, когда центр кривизны зеркала не расположен в призме ("призма не в центре"). Пусть N – есть точка, в которой ось О пересекает призму. L – длина отрезка СN. Падающий луч в точке A разделяется на два луча 1 и 2. Лучи 1 и 2, образующие между собой угол, падают на зеркало в точках L1 и L2. Затем лучи направляются снова к призме и их мнимые продолжения сходятся в точке A` – изображение точки А по отношению к зеркалу M. На рис. 5.1 L – отрицательная величина. Лучи 1 и 2 пересекают призму второй раз соответственно в точках u1 и u2 и каждый из них отклоняется еще раз на угол q/2. Лучи выходят из призмы слегка расходящимися. В приближении Гаусса можно показать, что мнимые продолжения лучей сходятся на зеркале, в точке L середины L1L2. Лучи 1 и 2 проходят через фокусирующий объектив и сходятся на экране в точке L`, сопряженной с L по отношению к объективу О.
Начальная разность хода D между лучами 1 и 2 после их второго пересечения призмы равна сумме разности db оптических длин в воздухе от точки A до точки L` и разности dn оптических длин в призме. Согласно свойству идеальной оптической системы db=0. Поэтому для получения D достаточно вычислить dn. Пусть u и T есть точки, в которых соответственно прямая LA` и радиус LC пересекает призму. От вершины зеркала направим ось OX перпендикулярно к средней плоскости П призмы. Пусть x– абсцисса плоскости П, x – абсцисса точки L; x(A), x(u) и x(T)= -xx/R - абсциссы точек А, u и T. В соответствии с формулой для разности оптических путей D,
D= q(x-x), (5.1)
Имеем
dm = q[x(A)-x]+ q[x(u)-x].
В приближении Гаусса точка Т находится в середине отрезка Au, следовательно
D = q[x(A)+x(u)-2x] = -2q[x-x(T)] = -2q(x+zx/R). (5.2)
Этот результат не зависит от направления оси Ox. Разность хода в точке L` или в точке L не зависит от положения точки А в призме, т. е. положения светящейся точки источника. С широким источником света имеем, следовательно, полосы, локализованные на зеркале. Так как D зависит лишь от x, то полосы прямолинейны и перпендикулярны Ox.
Когда призма находится не в центре z¹0, то интерферометр настроен на полосы конечной ширины. Когда z=0, разность хода D постоянна по всему полю наблюдения. С немонохроматическим источником за анализатором наблюдается однородный свет. Цвет зависит от положения средней плоскости призмы. Следовательно, когда "призма в центре", интерферометр настроен на бесконечную полосу.
Исследуемый объект помещается перед зеркалом как можно ближе к нему. Основным недостатком интерферометра со сферическим зеркалом является то, что исследуемый объект находится в непараллельном световом пучке. Несовпадение светового пучка с самим собой при падении его на зеркало и после отражения от него может быть устранено использованием полупрозрачного зеркала за счет значительного (примерно в 4 раза) уменьшения освещенности.
Пусть сферическое зеркало интерферометра имеет R=400 см, а расстояние между фокусами светового пучка - 2 см. Если расстояние между зеркалом и объектом составляет 10 см, то расхождение точек встречи луча с объектом составляет 0,05 см. Во многих случаях такое смещение, если его направить в сторону наименьшего изменения толщины неоднородности, не вносит заметной ошибки. В этих условиях ошибка в основном будет вызываться отклонением луча в неоднородности.
Используя линзу и плоское зеркало или вогнутое и плоское зеркало, можно получить такой автокомпенсационный интерферометр, в котором исследуемый объект будет находиться в параллельном пучке. Интерферометр, схема которого приведена на рисунке 1, можно преобразовать так, что световой пучок будет проходить через исследуемый объект 4 раза и, тем самым, чувствительность интерферометра будет повышена еще в два раза.
II. Юстировка и настройка поляризационных интерферометров
Юстировка автокомпенсационных интерферометров осуществляется согласно "правилу равных освещенностей" (см. лабораторную работу №4 "Поляризационный интерферометр сдвига на базе теневого прибора Теплера ИАБ-458" данного описания).
6. Изучение работы и снятие характеристик газового лазера
Лабораторная работа знакомит студентов со свойствами излучения оптического квантового генератора работающего на смеси газов Не-Ne, применяемого в качестве источника света в оптических установках.
Такой источник световой энергии состоит из активной среды, обеспечивающей усиление оптического сигнала, и резонатора. Последний создает положительную обратную связь, необходимую для генерации. Свойства излучения лазера - монохроматичность, направленность, когерентность - обусловливаются свойствами как активной среды, так и резонатора. Характеристики отдельно взятых резонатора или активной среды существенно отличаются от соответствующих характеристик лазера.
I. Активная среда оптического квантового генератора
1. для того чтобы уяснить себе, как работает газовый лазер, сначала рассмотрим упрощенную атомную систему, в которой возможны лишь два состояния: невозбужденный (основной) уровень, обозначим его 1 (см. рис. 6.1) и возбужденный уровень 2.
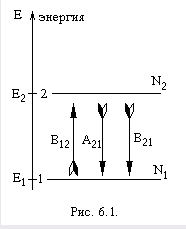
При температуре 0oК все атомы такой системы находятся на первом уровне, а при повышении температуры начинает заселяться и уровень 2, и чем больше температура, тем больше атомов перейдет с уровня 1 на уровень 2. Обозначим N1 - число атомов в единице объема на уровне 1, N2 - число атомов в единице объема на уровне 2. В случае термодинамического равновесия с окружающей средой при температуре ToK распределение атомов по состояниям подчиняется закону Больцмана:
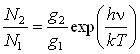 , (6.1)
, (6.1)
где hn=E2 - E1,
g1, g2 - кратности вырождения уровней 1 и 2 соответственно.
Естественно, что часть атомов с уровня 2 будет спонтанно переходить на уровень 1 и, если переход 2®1 излучательный, то появится спонтанное излучение. Если на уровне 2 находится N2 атомов, то полное число переходов в секунду с уровня 2 на уровень 1 будет N2A21, где A21 - вероятность перехода с уровня 2 на уровень 1.
Заметим, что это излучение некогерентно: фазы электромагнитных колебаний, излученных разными атомами, не связаны между собой.
2. Теперь представим себе, что на нашу атомную систему падает извне излучение с плотностью rv и частотой, удовлетворяющей соотношению
hn = E2 - E1.
В этом случае, кроме спонтанных переходов, появляются, еще и вынужденные (индуцированные) переходы с уровня 2 на уровень 1 и полная вероятность того, что атомная система перейдет с уровня 2 на уровень 1 (за единицу времени), будет
r21 = A21 + rvB21, (6.2)
где B21 - вероятность индуцированного перехода.
Заметим, что вынужденное излучение уже не является хаотическим, его фаза будет совпадать с фазой внешнего излучения. Совпадают также и остальные характеристики: волновые векторы, поляризации и частоты.
Попадающее в вещество внешнее излучение вызывает также и переходы с уровня 1 на уровень 2 с вероятностью r12 = rvB12. Между величинами А и В (их называют коэффициентами Эйнштейна) существует связь
g1B12 = g2B21,
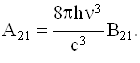 (6.3)
(6.3)
Внешнее излучение, попадая в вещество, будет поглощаться, и нарушать термодинамическое равновесие атомной системы. Рассмотрим взаимодействие такого ансамбля атомов с излучением на частоте n. Число переходов в секунду с уровня 2 на уровень 1 будет (A21+ rvB21)N2, а число переходов с уровня 1 на уровень 2 rvB12N1.
Потери падающего пучка электромагнитного излучения будут составлять: (N1- N2)rvB12 (6.4) квантов в секунду, и при N1- N2<0 излучение при прохождении через вещество будет ослабляться. Испущенные A21N2 квантов в секунду дадут рассеянное (по направлению) излучение и поэтому в формуле (6.4) не фигурируют. Интенсивность излучения будет убывать внутри вещества по закону:
![]() , (6.5)
, (6.5)
где JO - интенсивность на входе в вещество,
Kn - коэффициент поглощения на частоте n.
В газовом разряде возбуждается линейчатый спектр, и поглощение происходит лишь в пределах ширины спектральных линий. Контур их чаще всего определяется доплеровским уширением.
Типичная зависимость Kn от частоты показана на рис. 6.2. существует связь между площадью под кривой Kn(n) и разностью населенностей уровней [см. 4]:
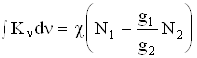 , (6.6)
, (6.6)
где 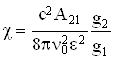 - интегральное (по
частотам) поперечное сечение поглощения одного атома.
- интегральное (по
частотам) поперечное сечение поглощения одного атома.
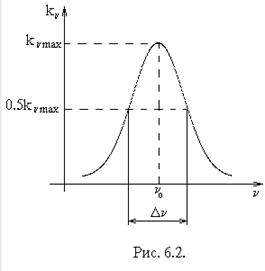
Таким образом видно, что интегральный коэффициент поглощения атомной системы будет положительным при N2<N1, что обычно имеет место, так как населенность верхних уровней атомной системы (если не принимать специальных мер), всегда меньше населенности основного уровня.
Представим себе, что нашли способ сделать так, что населенность верхнего уровня стала больше населенности нижнего уровня. В этом случае коэффициент поглощения будет отрицательным и атомная система с инверсной населенностью будет усиливать падающее в нее излучение по закону
![]() , где a=-Кn >0.
, где a=-Кn >0.
Если замкнуть такой усилитель цепью обратной связи, то можно получить оптический генератор.
3. Рассмотрим теперь, каким образом создается инверсия населенности в газовом Не-Ne лазере. Конструктивно Не-Nе лазер представляет собой стеклянную трубку, наполненную смесью гелия и неона и помещенную в оптический резонатор. С помощью высоковольтного источника питания в трубке создается разряд постоянного тока и этим возбуждаются атомы обоих газов.
Состояния Не, соответствующие уровням 21SO и 23S1 (см. рис. 6.3), являются метастабильными - переходы с этих уровней в основное, невозбужденное состояние запрещены в дипольном приближении, а других уровней, лежащих между основным состоянием и 21SO и 23S1 нет.
Практически это выражается в том, что время жизни этих уровней в 104-105 раз больше времени жизни других уровней, с которых имеются разрешенные дипольные переходы. Поэтому в результате переходов с верхних уровней атомы скапливаются в этих состояниях.
В энергетическом спектре Ne состояния 2S (символика Пашена) и 3S (точнее, четыре состояния каждого типа) случайно оказались совпадающими с метастабильными уровнями Не. Благодаря этому в возбужденной смеси Не и Ne происходит обмен энергией, носящий резонансный характер, между возбужденным Не в состояниях 21SO и 23S1 и невозбужденными атомами Ne. В результате неупругих столкновений с Ne метастабильные состояния Не разрушаются, а Ne возбуждаются в 3S и 2P состояния:
He*(21SO)+Ne ® He.
Разряд возбуждает практически все уровни Ne, заселяя их приблизительно в соответствии с больцмановским законом. В результате резонансного взаимодействия Не с Ne происходит дополнительное избирательное дозаселение уровней 3S и 2S Ne. Процесс оказался достаточно эффективным, чтобы обеспечить инверсию на некоторых переходах, начинающихся с 2S и 3S.
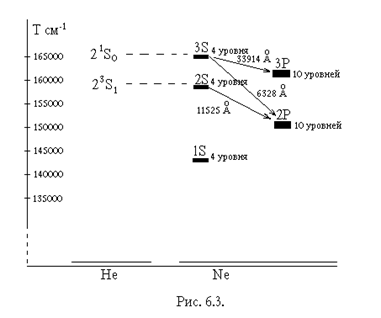
С уровней типа 3S существуют разрешенные переходы на уровни типа 3P и 2P (всего около 60 переходов), а с уровней типа 2s на 2Р (около 30 переходов), наиболее сильная генерация наблюдается на следующих переходах:
3S2 ® 2P4![]() ;
;
3S2 ® 3P4![]() ;
;
2S2 ® 2P4![]() .
.
4. Конструкция лазера, используемого в данной лабораторной работе, представляет собой разрядную трубку, заполненную смесью газов Не и Ne, и помещенную в оптический резонатор. Излучение из трубки выходит через два окна из оптического стекла, расположенных под углом Брюстера к оси трубки. Такой наклон окон позволяет свести к нулю отражение на границе стекло - (Не и Ne) и стекло - воздух для определенной поляризации световой волны. Этим заметно уменьшаются потери в резонаторе, так как при окнах расположенных перпендикулярно оси резонатора, френелевское отражение на границе стекло - воздух составляет около 4%.
Зеркала резонатора имеют диэлектрическое покрытие, нанесенное методом вакуумного напыления на кварцевые или стеклянные подложки. Пленка покрытия имеет толщину порядка нескольких длин волн и может быть легко повреждена при неосторожном обращении.
II. Резонатор оптического квантового генератора
Как и в диапазоне СВЧ, в
оптическом диапазоне наиболее эффективное взаимодействие электромагнитного поля
с активной средой осуществляется при помещении ее внутрь резонатора. Однако в
оптическом диапазоне не могут быть использованы резонаторы, моделирующие (в
отношении длин волн) типичные системы диапазонов СВЧ, размеры которых порядка
длины волны, а спектр собственных частот в рабочем диапазоне разрежен настолько,
что в конкретных приложениях оказывается возможным ограничиться рассмотрением
лишь нескольких или даже одного типа колебаний. Дело здесь не только в
трудности изготовления резонаторов микроскопически малых размеров, и в
недостаточной их вместимости для получения значительных мощностей. Есть
обстоятельства принципиального характера, которые практически ограничивают
область применения резонаторных систем с размерами порядка длины волны
миллиметровым диапазоном. Одним из этих обстоятельств является увеличение
потерь в стенках с ростом частоты электромагнитных колебаний (при нормальном
скин-эффекте, как ![]() ).
).
Это диктует необходимость перехода в коротковолновых диапазонах к многомодовым резонаторам, размеры которых велики по сравнению с длиной волны, и, следовательно, собственные типы колебаний, попадающие в рабочий диапазон активного вещества, имеют высокий порядок.
Но и в этом случае использование замкнутых резонансных объемов, характерных для диапазона СВЧ, оказывается не приемлемым. Это связано со сгущением собственных частот таких резонаторов при переходе к более высоким типам колебаний. Число типов колебаний замкнутой полости объема V, приходящихся на интервал частот Dw, равно
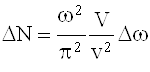 , (6.7)
, (6.7)
где v - скорость света в веществе, заполняющем резонатор.
Резонансные кривые при этом оказываются перекрывающимися, и, следовательно, резонатор теряет свои резонансные свойства. Таким образом, для успешного применения многомодовых резонаторов в оптическом диапазоне необходимо найти: 1) пути разрежения их спектра; 2) желательно при одновременном уменьшении потерь энергии в резонирующем объеме. Таких путей, в принципе, может быть несколько. В настоящее время наибольшее распространение получил способ разряжения спектра при сохранении высоких значений добротности, заключающийся в применении открытых резонаторов, в частности, резонаторов типа интерферометра Фабри-Перо [см. литературу 1, 2].
Интерферометр Фабри-Перо представляет собой систему из двух плоских или сферических зеркал, установленных параллельно друг другу или (случай сферических зеркал) таким образом, чтобы их оптические оси совпадали.
В классической оптике используются обычно пассивные интерферометры, световая энергия, к которым подводится от внешнего источника. Расстояние между зеркалами сравнимо с диаметром зеркал и имеют порядок одного - нескольких сантиметров. При такой геометрии дифракционные потери на краях зеркал даже с учетом многократности отражения не существенны и внутреннее поле резонатора фактически представляет собой поле однородных плоских волн.
Если излучение источника света можно представить в виде суммы бесконечного числа плоских волн, то действие такого интерферометра сводится к селекции некоторых из них, остальные же отражаются зеркалами Фабри-Перо в сторону источника света.
В работающем лазере мощность подводится только из внутренних областей интерферометра, а многократные потери мощности из-за дифракции на краях вызывают заметные нарушения однородности амплитуды и фазы волны у зеркала.
Что же тогда подразумевать под типами колебаний ("модами") такого резонатора? И существуют ли они вообще? Впервые эта проблема рассмотрена в работе А.Фокса и Т.Ли [см. литературу 1]. В этой работе путем численного расчета, выполненного на ЭВМ показано, что в двухзеркальном интерферометре, как со сферическим, так и с плоскими зеркалами могут существовать стационарные распределения поля, которые являются результатом многократных проходов волн между зеркалами. Эти стационарные распределения и называют модами резонатора. При расчете Фокс и Ли брали однородное распределение амплитуды и фазы на поверхности одного зеркала и вычисляли распределение амплитуды и фазы на поверхности другого. Полученная функция использовалась для следующего вычисления и так далее. После того, как волна испытывает 300 отражений, флюктуации, наблюдающиеся от прохода к проходу, составляют менее 0.03% от средней величины - распределение можно считать стационарным.
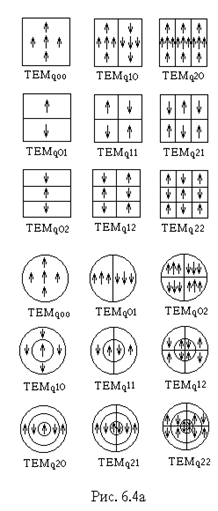
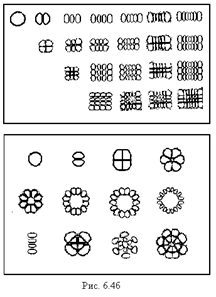
Моды обозначают символом ТЕМqmn ; ТЕМ - чтобы показать, что электрические и магнитные поля в большинстве случаев перпендикулярны (Т®"transversal") продольной оси резонатора; индексы m, n отличают одну конфигурацию поля на поверхности зеркала от другой - они обозначают число изменений знака поля на зеркалах резонатора:
а) в случае прямоугольных зеркал - по осям x и y (рис. 6.4a),
б) в случае круглых зеркал по радиусу r и углу j (при изменении последнего от 0 до p) (рис. 6.4б).
Индексы m, n таким образом, отличают одну поперечную моду от другой. Для каждой поперечной моды существует последовательность продольных мод, характеризующихся разными значениями индекса q; индекс показывает число полуволн, укладывающихся вдоль длины резонатора.
На рис. 6.4а представлено символическое изображение распределения поля на прямоугольном и круглом зеркалах, соответствующее различным поперечным модам. На рис. 6.4б приведены фотографии распределения интенсивности по поперечному сечению луча лазера для некоторых типов колебаний.
Каждой моде ТЕМqmn соответствует вполне определенная резонансная частота n. Для резонатора, образованного плоскими зеркалами, n можно вычислить, пользуясь выражениями, приведенными в работе [3]:
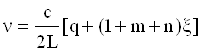 , (6.8)
, (6.8)
где L - расстояние между зеркалами резонатора;
c - скорость света;
x - коэффициент расщепления.
Коэффициент расщепления с точки зрения геометрической оптики определяет, как в пространстве разнесены лучи, образующие тот или иной поперечный тип колебаний (моду). Величина коэффициента x определяется геометрическими размерами и может быть вычислена по формуле
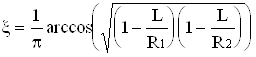 , (6.9)
, (6.9)
где R1 и R2 - радиусы кривизны зеркал.
Из формулы (6.8) следует, что разность частот между соседними продольными модами, соответствующими одному поперечному распределению (одной поперечной моде: m=const, n=const) равна
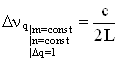 , (6.10)
, (6.10)
причем эта величина одна и та же для всех поперечных мод.
Типы колебаний с одинаковыми значениями суммы индексов (вырожденные типы колебаний) имеют, согласно формуле (6.8), совпадающие (при одинаковых q) резонансные частоты, но различное распределение поля в поперечном сечении луча. Однако в реальном резонаторе вследствие наличия в нем активной среды и асимметрии резонансные частоты вырожденных типов колебаний несколько отличаются.
В лазере генерация происходит на частотах, близких к резонансным частотам резонатора и заключенных в пределах ширины линии ансамбля атомов, где им соответствует заметный коэффициент усиления. Это иллюстрирует рис. 6.5, на котором показана "естественная" ширина атомной линии, ширина линии излучения ансамбля атомов, обусловленная доплеровским уширением, и частотный спектр резонансных мод [см. литературу 4].
При расстоянии между зеркалами L=1 м, Dn=150 МГц. Так как доплеровская ширина линии составляет величину около 900 МГц, то одновременно могут быть возбуждены несколько продольных мод, соответствующих определенному поперечному распределению интенсивности. Из рис. 6.5 видно, что порог самовозбуждения для различных мод будет неодинаков. Поэтому меняя величину разрядного тока или ухудшая добротность резонатора можно возбудить одну моду (одномодовый режим генерации).
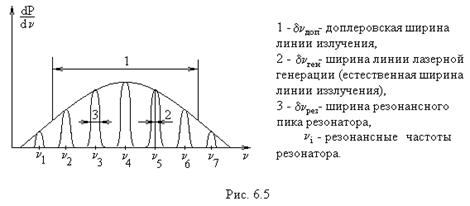
Спектральная ширина моды существенно уже ширины, определяемой добротностью резонатора.
III. Интерферометр Фабри-Перо
Для исследования спектрального состава излучения газового лазера в данной лабораторной работе используется прибор, обладающий высокой разрешающей силой - эталон Фабри-Перо.
Для выполнения работы необходимо ознакомится с теорией эталона Фабри-Перо [2].
Интерферометр, предложенный в 1897 году Фабри и Перо, удивляет простотой своего устройства и удобством применения. Интерферометр Фабри-Перо состоит из двух плоских и параллельно расположенных стеклянных или кварцевых пластин (зеркал), покрытых полупрозрачным слоем металла с высоким коэффициентом отражения, порядка 80-90%. В последнее время все чаще в интерферометрах применяются зеркала с многослойными диэлектрическими покрытиями, для которых может быть обеспечен еще более высокий коэффициент отражения при исчезающе малых потерях в отражающих покрытиях. Если на две такие пластины, расстояние между которыми равно l см., падает свет с длиной волны l от сравнительно большого по размерам источника, то получаются кольца равного наклона. Практически картину колец можно наблюдать в фокусе линзы, помещенной после интерферометра. Свет, падающий вдоль поверхности конуса с углом q, дает светлое кольцо, если выполняется условие
ml = 2nl×cos(q), (6.11)
где m - порядок интерференции, n - показатель преломления cреды между пластинами. Обычно этой средой является воздух, поэтому можно принять без особой ошибки, что n=1.
Так как, cos(q) принимает максимальное значение при q=0, то центральное кольцо соответствует наибольшему порядку интерференции m. При переходе к каждому из последующих колец порядок интерференционного максимума m убывает на единицу.
Изменяя длину интерферометра l, можно достигнуть желаемого интервала в длинах волн между максимумами соседних порядков. Этот интервал Dl равен
Dl = l2/(2l) (6.12)
и называется областью дисперсии интерферометра.
Распределение интенсивности в полосах интерферометра Фабри-Перо выражается классической формулой Эйри.
Пусть Т и R обозначают
соответственно коэффициенты пропускания и отражения зеркал интерферометра (если
пренебречь потерями в покрытиях зеркал, то Т=1-R). Тогда распределение
интенсивности в полосах легко выразит как функцию разности фаз d между двумя соседними лучами. Для
света, падающего под углом q, разность хода между соседними лучами, испытывающими многократное
отражение, рана 2nl×cos(q). Отсюда
разность фаз равна ![]() . Распределение
интенсивности в полосах выражается в этом случае формулой
. Распределение
интенсивности в полосах выражается в этом случае формулой
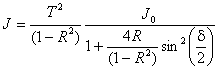 , (6.13)
, (6.13)
где JO -
интенсивность света, падающего на интерферометр. Так как ![]() меняется от 0 до 1, то
интенсивность непрерывно изменяется от максимального значения
меняется от 0 до 1, то
интенсивность непрерывно изменяется от максимального значения 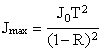 до минимального значения
до минимального значения 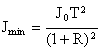 . Распределение
интенсивности может быть записано в виде:
. Распределение
интенсивности может быть записано в виде:
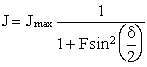 , (6.14)
, (6.14)
где ![]() . Величина зависящая только
от коэффициента отражения R, определяет резкость полос, и поэтому Фабри назвал
ее "коэффициентом резкости".
. Величина зависящая только
от коэффициента отражения R, определяет резкость полос, и поэтому Фабри назвал
ее "коэффициентом резкости".
Важной характеристикой
интерферометра Фабри-Перо является предел разрешения dl и разрешающая сила ![]() .
.
Согласно критерию Рэлея, две линии равной интенсивности считаются разрешенными, если минимум интенсивности суммарного контура линии составляет приблизительно 0.8 интенсивности каждого из двух равных максимумов. Применяя этот критерий к уравнению (6.13), можно получить
![]() , (6.15)
, (6.15)
или переходя к волновым
числам ( см-1):
см-1):
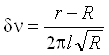 . (6.16)
. (6.16)
Длину интерферометра Фабри-Перо l при заданном коэффициенте отражения R выбирают исходя из того, какое необходимо обеспечить разрешение dl и какой диапазон Dl занимают анализируемые длины волн.
IV. Описание экспериментальной установки
Схема установки приведена на рис. 6.6.
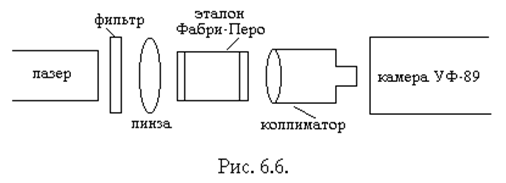
В состав установки входят:
· фабричный лазер типа ЛГН-215 (длина
волны излучения l=6328![]() );
);
· эталон (интерферометр) Фабри-Перо;
· фотографическая камера УФ-89;
· набор линз, вставляемых в держатель;
· набор светофильтров (фильтры могут вставляться в специальный держатель);
· матовое стекло;
· лупа для рассматривания картины на матовом стекле камеры УФ-89.
Установка смонтирована на оптической скамье.
В настоящей лабораторной работе используется интерферометр Фабри-Перо типа ИТ-17а. Прибор установлен на оптический столик, который может наклоняться или разворачиваться в горизонтальном направлении с помощью винтовой подачи. Зеркала интерферометра - плоские тщательно обработанные стеклянные пластины с напыленными зеркальными слоями, зажаты внутри полированного корпуса с помощью трех юстировачных винтов. Диэлектрические слои зеркал обращены навстречу друг другу, внутрь корпуса.
Чтобы избежать помех от добавочной интерференции лучей, отражающихся от зеркальной и незеркальной поверхностей, пластина обычно изготовляется так, чтобы две ее поверхности составляли угол от 1o до 30¢ (в нашем интерферометре 30¢).
Расстояние между зеркалами в ИТ-17а может варьироваться от 0.3 до 50 мм. Для этой цели в комплект интерферометра входит набор распорных промежуточных колец, изготовленных из инвара или плавленного кварца. Промежуточное кольцо имеет с каждой стороны три выступа, прошлифованных до равной толщины с высокой точностью. Степень параллельности очень высока: например, кольцо длиной 150 мм отличается от номинала в различных точках не более чем 10-4 мм. Зеркала прижимаются к выступам на промежуточном кольце с помощью трех легких юстировочных винтов, действующих на одно из зеркал через упругие стальные пластины. Второе зеркало фиксируется опорным кольцом.
Для выполнения задачи интерферометр собран с распорным кольцом толщиной l=150 мм. Учитывая, что коэффициент отражения зеркал R=95%, область дисперсии прибора (6.12) будет:
Dl=1.3×10-2 ![]() (Dn=3×10-2 см-1)
(Dn=3×10-2 см-1)
а теоретически предел разрешения (6.15)
dl=6×10-4 ![]() (Dn=1.5×10-3 см-1).
(Dn=1.5×10-3 см-1).
Практическое разрешение прибора во многом зависит от качества его юстировки.
Юстировка интерферометра Фабри-Перо. Способы параллельной установки зеркальных поверхностей интерферометра зависят от величины промежутка между пластинами. Для промежутков меньше 2 см юстировка параллельности относительно легка, для промежутков от 2 до 5 см она несколько труднее, а для промежутков больше 5 см - очень трудна. С увеличением расстояния между зеркалами интерферометра угловой диаметр колец постепенно уменьшается, и кольца для глаза начинают сливаться. Поэтому при больших толщинах промежуточного кольца приходится пользоваться зрительной трубой, установленной на бесконечность. Кроме того, при увеличении толщины промежуточного кольца область дисперсии интерферометра уменьшается, в то время как спектральная ширина используемого источника света остается, естественно, неизменной. Поэтому общая резкость картины колец падает. Желательно пользоваться при юстировке источником, дающим минимальное количество спектрально "узких" и ярких линий. Уникальным источником в этом смысле является газовый лазер, работающий в режиме, когда генерируется малое число (1-4) продольных мод.
Наиболее распространен следующий способ юстировки интерферометра.
Согласно формуле (6.11) угловой диаметр какого-либо (выбранного) кольца зависит от величины промежутка между зеркалами, поэтому, если зеркала параллельны, то при перемещении глаза (аккомодированного на бесконечность) вдоль пластин интерферометра диаметр колец не должен изменяться. Если же между пластинами имеется небольшой угол, то при движении глаза в направлении от вершины к основанию клина кольца будут стягиваться к середине системы, параллельность пластин достигается путем легкого нажима на ту пружину, по направлению к которой кольца расширяются.
Центр системы особенно чувствителен к изменению толщины промежутка. Если картина колец наблюдается через зрительную трубку, то вместо глаза можно перемещать диафрагму с отверстием 5-6 мм, которая располагается между интерферометром Фабри-Перо и объективом зрительной трубы. При этом следует помнить, что обычно используемые зрительные трубы системы Кеплера переворачивают изображение.
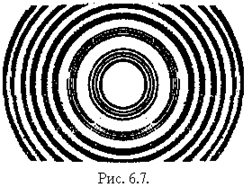
При величинах промежутков между зеркалами l³10 мм юстировку интерферометра производят обычно без диафрагмы по общей четкости картины колец. Зрительная труба при этом должна быть особенно тщательно установлена на бесконечность, а ее апертура не меньше апертуры Фабри-Перо. Кольца оказываются "нерезкими" в том направлении, в котором наклонено зеркало. Юстировку можно считать выполненной, если кольца (хотя бы в двух центральных порядках) надежно разрешаются в любом месте (рис. 6.7).
Обработка интерферограммы. Если в падающем на интерферометр Фабри-Перо излучении содержится р близких спектральных компонент, то каждый порядок в интерференционной картине будет расщеплен на р колец (если предел разрешения dl меньше спектрального интервала между компонентами).
Для того чтобы интерферограмму можно было обработать, ширина анализируемого спектра должна быть меньше области дисперсии интерферометра Dl.
Измерив диаметры колец, соответствующих интересующим нас спектральным компонентам (а и b), можно вычислить разность между компонентами в волновых числах (в см-1) по формуле
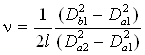 , (6.17)
, (6.17)
где  - волновое число; Db1
и Da1 - диаметры колец одного порядка интерференции, принадлежащих
двум разным частотам; Da2 - диаметр кольца следующего, более
низкого, порядка, принадлежащего одной из частот.
- волновое число; Db1
и Da1 - диаметры колец одного порядка интерференции, принадлежащих
двум разным частотам; Da2 - диаметр кольца следующего, более
низкого, порядка, принадлежащего одной из частот.
Камера УФ-89
Камера УФ-89 состоит из длиннофокусной линзы (F=800 мм) и фотокассеты. Кассетную часть камеры можно передвигать относительно линзы для получения резкого изображения на фотопластинке ("настройка на резкость"). Камера может перемещаться во всех направлениях. При необходимости кассета может быть заменена на матовое стекло.
Кассетная часть снабжена выдвижной шторкой с прорезью (диафрагмой) которая ограничивает засвеченное поле горизонтальной полоской высотой 7 мм.
Передвигая кассету в вертикальном направлении (имеется механизм для калиброванного смещения), можно на одну фотопластинку сделать несколько снимков.
Кассета заряжается
фотопластинами размером 9х12. Для фотографирования излучения с длиной волны l=6328![]() лучше
всего использовать пластины "панхром". Вместо пластины в кассету
может быть помещен отрезок пленки (располагается вертикально).
лучше
всего использовать пластины "панхром". Вместо пластины в кассету
может быть помещен отрезок пленки (располагается вертикально).
6. Изучение работы и снятие характеристик импульсного оптического квантового генератора
преломление оптический свет квантовый
Оптическими квантовыми генераторами (ОКГ) на твердом теле называются такие приборы, в которых в качестве активной управляющей среды используется кристаллический или аморфный диэлектрик. Примерами твердотельных ОКГ могут служить широкоизвестные рубиновые ОКГ или генераторы на стекле, активированные неодимом. Для них инверсия населенности образуется на энергетических уровнях атомов и ионов вещества, находящегося в твердом агрегатном состоянии. Причем концентрация активных частиц в твердом материале на несколько порядков превышает концентрацию активных частиц в газовых средах. Поэтому в твердом теле абсолютная величина инверсии населенности может быт существенно больше, чем в газах. Отсюда понятно, что твердые активные среды должны характеризоваться высоким коэффициентом усиления. Это в свою очередь позволяет получать большие мощности генерации и добиваться генерации при малой длине активного элемента.
Твердое тело как оптическая среда обладает гораздо меньшей оптической однородностью по сравнению с газами. Это приводит к возникновению объемных потерь на рассеяние, снижению добротности резонатора при значительной длине активного элемента. Поэтому активные элементы твердотельных ОКГ имеют длину не более 50-60 см. для наиболее оптически однородных материалов. Оптическая неоднородность среды приводит к тому, что сверхпороговая инверсия создается не по всему сечению активного элемента, а в определенных узких каналах. Поэтому угол расхождения пучка генерируемого излучения, оцениваемый даже из дифракционных соображений, оказывается значительным.
В твердом теле взаимодействие между частицами существенно искажает структуру энергетических уровней. Так для спонтанного излучения характерна ширина полосы в несколько ангстрем. Ширина линии генерации в лучшем случае составляет доли ангстрем.
Способ создания инверсии в твердотельных ОКГ принципиально отличается от накачки газовых лазеров. Он не может быть связан с прохождением электрического тока через твердый диэлектрик. Для них характерна оптическая накачка, при которой заселение возбужденных состояний достигается путем интенсивного облучения активного элемента излучением внешнего источника. Специально подобранный спектральный состав этого излучения или определенное соотношение между вероятностями соответствующих переходов приводит к преимущественному заселению верхнего рабочего уровня и возникновению инверсии.
Действие ОКГ на твердых телах основано на тех же квантовомеханических принципах, что и газовые лазеры. Поэтому, здесь, основные математические выкладки, показывающие условия генерации в твердотельных ОКГ, не приводятся (смотрите лабораторную работу №6 "Изучение работы и снятие характеристик газового лазера").
Цель лабораторной работы - ознакомить студентов с принципом работы твердотельных ОКГ и свойствами его излучения, на основе активного элемента рубина.
I. Рубин как активная среда для импульсных ОКГ.
Рубин - кристаллический минерал, имеющий окраску от бледно-розового до ярко-красной. Структурой рубина является кристаллическая решетка Al2O3 с внедренными в нее трехзарядными ионами хрома Cr3+. Содержание хрома колеблется обычно в пределах от 0.05 до 0.5 %. Цвет кристалла определяется содержанием хрома - чем больше хрома, тем более красный оттенок имеет рубин. Рубин обладает очень большой твердостью, а также хорошей теплопроводностью, что способствует быстрому охлаждению рубинового стержня. Он вырезается в виде цилиндрического стержня, торцы которого шлифуются до параллельности.
Активный элемент - рубин ОКГ должен удовлетворять следующим требованиям:
* допускать активировку элементами, на которых осуществляется генерация;
* быть химически стойким и механически прочным, чтобы обеспечить долговечность среды;
* выдержать значительные нагревы, которые возможны при высокой плотности излучения оптической накачки и генерации;
* технология должна быть доступна для массового производства;
* быть прозрачным для излучения накачки и генерации;
* быть оптически однородным, так как рассеяние на неоднородностях среды вносит дополнительные потери и снижает добротность резонатора.
Электронная конфигурация основного состояния трехзарядного иона хрома-3.
Вследствие взаимодействий между ионами кристаллической решетки основное состояние расщеплено на ряд уровней. Схема нижних энергетических уровней приведена на рис. 7.1. Два близко расположенных уровня 2 - метастабильные долгоживущие состояния. Время жизни данного состояния в квантовой механике определяется суммой вероятностей всех спонтанных переходов в низшие состояния 1
![]()
где t2 - характеризует время, в течение которого населенность состояния уменьшается в е раз.
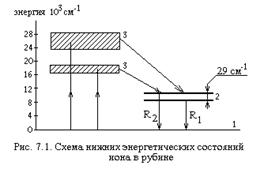
Ширина энергетического уровня DW2 связана со временем жизни данного состояния соотношением:
DW2 = h/t2,
где h – постоянная Планка.
Таким образом, чем больше время жизни данного состояния, тем меньше ширина его энергетического уровня.
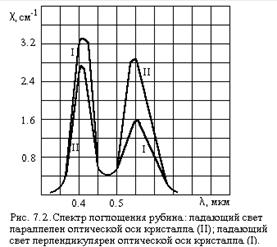
Переход 2 ® 1 в трехзарядном ионе Cr3+ запрещен правилом отбора. Два широких уровня 3 соответствуют состояниям с малым временем жизни, причем наиболее вероятен спонтанный переход 3 ® 2. Этот переход безизлучательный - избыток внутренней энергии иона переходит в тепловую энергию кристаллической решетки.
Инверсное заселение состояний происходит по трехуровневой схеме.
Излучение накачки поглощается в кристалле на переходах 1 ® 3.
Спектр поглощения рубина
соответствует раздвоенной структуре состояния 3. Он содержит две широкие (Dl»1000![]() ) полосы поглощения, максимумы
которых приходятся на зеленую и фиолетовую области спектра. Спектр поглощения
рубина представлен на рис. 7.2, где две зависимости соответствуют двум
ориентациям падающего излучения относительно оптической оси кристалла. В
результате поглощения излучения накачки ионы хрома переходят в одно из
состояний 3. Затем за счет спонтанного безизлучательного распада этих состояний
ионы оказываются в метастабильных состояниях 2. Поскольку в данном случае
выполняется условие
) полосы поглощения, максимумы
которых приходятся на зеленую и фиолетовую области спектра. Спектр поглощения
рубина представлен на рис. 7.2, где две зависимости соответствуют двум
ориентациям падающего излучения относительно оптической оси кристалла. В
результате поглощения излучения накачки ионы хрома переходят в одно из
состояний 3. Затем за счет спонтанного безизлучательного распада этих состояний
ионы оказываются в метастабильных состояниях 2. Поскольку в данном случае
выполняется условие ![]() населенность
состояния 2 при соответствующей плотности накачки может превысить населенность
невозбужденного состояния и на переходах 2 ® 1 возникает генерация. В рубиновом ОКГ генерация
осуществляется на двух линиях, которые обычно обозначают R1 и R2.
Длина волны этих линий зависит от температуры кристалла, так как температура
изменяет характер внутрирешеточного расщепления основного ионного состояния.
Зависимость длины волны генерации от температуры кристалла является
специфической особенностью твердотельных ОКГ. Значение длины волны генерации на
рубине при комнатной и азотной температурах приведены в таблице 7.1.
населенность
состояния 2 при соответствующей плотности накачки может превысить населенность
невозбужденного состояния и на переходах 2 ® 1 возникает генерация. В рубиновом ОКГ генерация
осуществляется на двух линиях, которые обычно обозначают R1 и R2.
Длина волны этих линий зависит от температуры кристалла, так как температура
изменяет характер внутрирешеточного расщепления основного ионного состояния.
Зависимость длины волны генерации от температуры кристалла является
специфической особенностью твердотельных ОКГ. Значение длины волны генерации на
рубине при комнатной и азотной температурах приведены в таблице 7.1.
Таблица 7.1
| Линии |
l, |
|
|
T=300oK |
T=77oK |
|
|
R1 |
6943 | 6934 |
|
R2 |
6929 | 6929 |
Генерация на рубине в настоящее время реализуется как в импульсном, так и в непрерывном режиме. Для импульсного режима характерны миллисекундные импульсы генерации, в этом случае используются импульсные ксеноновые лампы. Пороговая энергия накачки зависит при выбранной лампе от объема и температуры кристалла, а также от конструкции системы накачки. Стержень и лампа обычно располагаются параллельно друг к другу внутри круглого цилиндрического осветителя, иногда используются эллиптические или же двойные эллиптические отражатели. В практике применяются кристаллы диаметром от (12-15) мм. и длиной (15-20) см. На торцы рубина наносится серебряное или диэлектрическое покрытие, так, чтобы один был полностью, а другой частично отражающим или же отшлифованный рубин помещается внутри открытого резонатора Фабри-Перо. Пороговая энергия для рубина составляет сотни джоулей, а коэффициент полезного действия не превышает 1%.
II. Монохроматичность и когерентность твердотельных ОКГ.
Одной из основных характеристик излучения является ширина его спектра, то есть диапазон частот или длин волн, который занимает излучение. Ширину спектра излучения удобно характеризовать степенью монохроматичности. В случае спектральной линии степень монохроматичности равна:
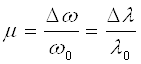
где ![]() полуширина линии, а
полуширина линии, а ![]() центральная частота.
центральная частота.
Если ![]() то излучение идеально
монохроматично. Если
то излучение идеально
монохроматично. Если ![]() то излучение
называется квазимонохроматическим или почти монохроматическим. Из определения
степени монохроматичности следует, что идеально монохроматическое излучение -
это излучение, ширина спектра которого равна нулю. Такое излучение можно
сопоставить лишь с колебанием электромагнитной энергией, бесконечной продолжительности.
то излучение
называется квазимонохроматическим или почти монохроматическим. Из определения
степени монохроматичности следует, что идеально монохроматическое излучение -
это излучение, ширина спектра которого равна нулю. Такое излучение можно
сопоставить лишь с колебанием электромагнитной энергией, бесконечной продолжительности.
В случае, когда излучение занимает протяженный участок спектра, степень монохроматичности определяется логарифмом отношения крайних частот спектра: m = ln(w2/w1) = 2.3 lg(l1/l2).
Современные ОКГ на рубине
имеют мощность в импульсе несколько киловатт, а некоторые ОКГ обладают
мощностью порядка сотен и тысяч мегаватт при площади сечения пучка 1 см2.
Излучение рубиновых ОКГ состоит из нескольких очень узких спектральных линий,
шириной примерно 10-4 - 10-3 ![]() .
.
В оптическом диапазоне излучения лазеров различают временную (разность фаз для двух фиксированных точек вдоль направления луча не зависит от времени или, то же самое, разность фаз измеренная в одной точке пространства в начале и конце фиксированного интервала времени Dt, не изменяется со временем) и пространственную (разность фаз для двух фиксированных точек в плоскости, перпендикулярной к направлению луча, не зависит от времени) когерентности.
При оценке временной когерентности весьма полезно пользоваться понятием длины когерентности источника. Предположим, что источник излучает монохроматический волновой цуг определенной длины l и, что мгновенные значения амплитуды можно одновременно измерить в двух точках z1 и z2, расположенных на одной нормали к волновому фронту. Если разность Dz= z2 - z1 немного меньше чем l, то в течение короткого периода может казаться, что источник обладает временной когерентностью. Интервал Dz=l, для которого сохраняется некоторая степень постоянства разности фаз во времени, есть мера длины когерентности волнового источника. Длину когерентности l можно выразить через произведение l=с×Dt, где Dt- время, в течение которого источник излучает непрерывный цуг. В голографии, как мы увидим, длина когерентности накладывает ограничение на допустимую разность в длине пути опорного и рабочего пучков.
Длину когерентности можно выразить через другие физические величины. Так, например, разложив одночастотный волновой цуг продолжительностью Dt на фурье-компоненты и, учитывая пропорциональность интенсивности света квадрату фурье-образа, можно установить связь длины когерентности с шириной полосы частот Dn
l=c/Dn
Временную когерентность можно также связать с контрастом полос интерференционной картины, то есть со степенью различия освещенности экрана в максимумах и минимумах. Количественной характеристикой контрастности интерференционной картины служит безразмерная величина - видность полос g, которую Майкельсон определил следующим образом:
![]()
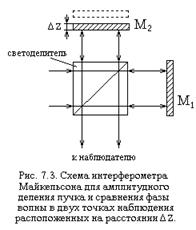
Контраст интерференционной картины зависит от размеров и формы источника света.
Методы амплитудного деления пучков (например, с помощью интерферометра Майкельсона) позволяют сравнить фазы плоской волны в различных точках вдоль направления распространения рис. 7.3.
Если наклонить одно из зеркал, то сравнение облегчается, поскольку в этом случае плоские волны, выделенные из пучка, пересекаются и образуют систему линейных интерференционных полос, интенсивность которых в плоскости наблюдения дается выражением:
![]()
Более общее выражение для интенсивности, справедливое и для частично когерентного света, можно получить заменяя комплексные амплитуды а1 и а2 комплексными напряженностями электрических полей v1, v2, и добавляя скобки, означающие усреднение по времени. Тогда:
![]()
Следует отметить, что операция усреднения по времени дает разные результаты в случае частичной и в случае абсолютной когерентности. Это проявляется в видности полос. При g=1 видность имеет максимальное значение, равное единице, что соответствует абсолютной когерентности.
Комплексная степень когерентности h(t), устанавливающая связь между электрическими полями Vp1(t) и Vp2(t) в точках p1 и p2 (как показано на рис. 7.4) и усредненным по времени интерференционным членом в точке Q определяется согласно Борну и Вольфу, как нормированная корреляция между Vp1(t) и Vp2(t):
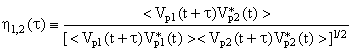 .
.
Связь между h(t) и ![]() устанавливается
формулой
устанавливается
формулой
![]() ,
,
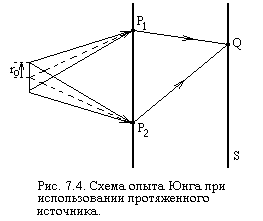
где J1 и J2 - интенсивности света, приходящих в точку Q из p1 и p2 соответственно, t - разность времени прохождения света в точку Q из точек p1 и p2, b1,2 - фаза величины h1,2(t).
Подставляя эти величины в выражение, определяющее видность полос, получим:
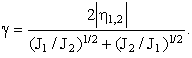
Когда интерферирующие волны имеют равную интенсивность, то видность полос определяется абсолютной величиной степени когерентности.
При t®0 видности полос, полученных в установке с двумя отверстиями (см. рис. 7.4), по существу является мерой пространственной когерентности. Согласно теореме Ван-Циттерта-Цернике степень пространственной когерентности связана с поперечным размером источника посредством преобразования Фурье. Здесь, мы, ограничимся формулировкой этой теоремы. Для протяженного источника, содержащего взаимные некогерентные осцилляторы излучения в узкой спектральной полосе шириной Dn теорема Ван-Циттерта-Цернике читается следующим образом: когда малый источник освещает две близко расположенные точки, лежащие в плоскости, находящейся на большом расстоянии от источника, степень когерентности комплексных электрических полей в этих двух точках дается величиной нормированного Фурье-образа распределения интенсивности источника.
В отличие от обычных источников ОКГ обладают высокой степенью пространственной и временной когерентности.
III. Мощность и направленность твердотельных ОКГ
Излучение, распространяющееся в пределах небольшого телесного угла, называется направленным. Направленный световой пучок должен иметь плоский или почти плоский волновой фронт.
Обычные источники обладают очень низкой направленностью излучения. Диаграмма направленности элементарных излучателей (атомов и молекул), из которых состоит источник, при определенной их ориентации характеризуется телесным углом примерно 2p. Параллельные лучи для этих источников можно получит при установлении диафрагмы на очень большом расстоянии от самого источника. Однако выделенные таким путем параллельные лучи несут небольшую часть энергии излучаемой источником. Почти параллельные лучи обычных источников можно также получить, если поместить источник в фокальной плоскости линзы коллиматора. Если при этом допустить, что источник представляет собой точку, аберрации оптики отсутствуют, то получим параллельный пучок, расходимость которого будет определяться дифракцией на линзе коллиматора. Здесь, как и в первом случае, энергия такого пучка будет ничтожной, так как источник очень малого размера будет излучать чрезвычайно малую энергию. Если же в фокальной плоскости линзы поместит источник конечных размеров, то коллиматор даст пучок с расходимостью равной размеру источника деленному на фокусное расстояние линзы.
Излучение твердотельных ОКГ является когерентным и поэтому фронт волны представляет собой почти плоскость или часть сферы большого радиуса. Расходимость для них определяется дифракцией на выходном отверстии.
Дифракционный угол расхождения лучей из ОКГ определяется соотношением:
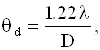
где l - длина волны излучения, D - диаметр излучающей поверхности.
Если в случае обычных источников степень параллельности лучей прямо связывается с энергией излучения, то для ОКГ такой непосредственной связи нет и поэтому почти параллельные лучи могут переносить большую энергию.
Мощность оптического излучения представляет собой энергию, переносимую излучением за единицу времени. Импульсная мощность определяется как отношение величины энергии в импульсе к длительности импульса:
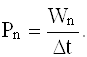
Средняя мощность определяет собой величину
![]()
где Т - период повторения импульсов.
Мощность, отнесенная к единице спектрального интервала, в котором происходит излучение, называется спектральной интенсивностью.
Мощность тепловых источников излучения определяется температурой и является вследствие этого ограниченной. По своей импульсной мощности и спектральной плотности интенсивности мощные ОКГ значительно превосходят все существующие источники излучения в оптическом диапазоне спектра.
ОКГ излучают всю энергию в узком спектральном диапазоне, оно когерентно и распространяется в пределах очень небольшого телесного угла.
| Лекции по Физической оптике | |
|
я2Московский Физико-Технический Институт я2Факультет Физической и Квантовой Электроники я_я3Л. Н. КУРБАТОВ. я_я3КВАНТОВАЯ ЭЛЕКТРОНИКА. я_я2Москва ... Пусть объектив равномерно освещен, т.е. U=const, ия2вычислим интеграл я2Т.е.я2Величина r=R/b есть угловой радиус на экране, соответствующийя2радиусу-вектору R точки Р. я2Идеальный ... 11.9 показаны главная ия2побочная оптические оси объектива, определяющие центры системя2колец на фокальной плоскости. |
Раздел: Рефераты по физике Тип: реферат |
| Оптоволоконные линии связи | |
|
Обзор существующих методов передачи на волоконно-оптических системах передачи городских телефонных сетей. 1.1.Принципы построения и основные ... В основе ВСМ/Д лежит известный объемный анализатор спектра типа эшелона Майкельсона, представляющий собой фазовую решетку со сравнительно небольшим числом интерферирующих лучей и ... Пучки, симметрично смещенные относительно щели, отклоняются призмой под углом 90° и направляются в отраженный канал (порт 3), где установлен двулучепреломляющий рутиловый элемент 9 ... |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Анализ погрешностей волоконно-оптического гироскопа | |
|
Содержание. Введение 1. Принципы волоконно-оптической гироскопии 1.1. Основные характеристики ВОГ Принцип взаимности и регистрация фазы в ВОГ Модель ... Луч света приходит в точку А и с помощью зеркал и расщепляется на два луча, один из которых распространяется по часовой стрелке в контуре, а другой - против часовой стрелки. Рассмотрение идеального кольцевого оптического контура с системой из двух зеркал позволяет получить тот же результат для разности времен распространения встречных лучей. |
Раздел: Рефераты по радиоэлектронике Тип: реферат |
| Реконструкция волоконно-оптической линии связи | |
|
Содержание Приложение 3 Введение 4 Обоснование реконструкции магистральной ВОЛС 6 Глава 1. Основные принципы цифровой системы передачи STM-64 7 1.1 ... 4.1.3. Компенсаторы хроматической дисперсии на основе планарных интерферометров и микро-оптических устройств. Мультиплексирование осуществляется с помощью специальных оптических призм, например, призмы Рошона. |
Раздел: Рефераты по коммуникации и связи Тип: реферат |
| Разработка систем передачи информации нового поколения | |
|
Содержание Введение 1. Основы технологии DWDM 1.1 Устройства волнового уплотнения DWDM 1.2 Модель взаимодействия DWDM с транспортными технологиями 1.3 ... Волоконная брэгговская решетка - это, по сути, оптический интерферометр, встроенный в волокно. Наиболее распространенные в оптике обычные дифракционные решетки отражают световой пучок под разными углами в плоскости падения, причем угол, в которых отраженный свет достигает ... |
Раздел: Рефераты по коммуникации и связи Тип: дипломная работа |