Реферат: Устойчивость линейной системы авторегулирования
Введение
Современная
теория автоматического регулирования является основной частью теории управления.
Система автоматического регулирования состоит из регулируемого объекта и элементов
управления, которые воздействуют на объект при изменении одной или нескольких регулируемых
переменных. Под влиянием входных сигналов (управления или возмущения), изменяются
регулируемые переменные. Цель же регулирования заключается в формировании таких
законов, при которых выходные регулируемые переменные мало отличались бы от требуемых
значений. Решение данной задачи во многих случаях осложняется наличием случайных
возмущений (помех). При этом необходимо выбирать такой закон регулирования, при
котором сигналы управления проходили бы через систему с малыми искажениями, а сигналы
шума практически не пропускались.
Теория
автоматического регулирования прошла значительный путь своего развития. На начальном
этапе были созданы методы анализа устойчивости, качества и точности регулирования
непрерывных линейных систем. Затем получили развитие методы анализа дискретных и
дискретно-непрерывных систем. Можно отметить, что способы расчета непрерывных систем
базируются на частотных методах, а расчета дискретных и дискретно-непрерывных —
на методах z-преобразования.
В
настоящее время развиваются методы анализа нелинейных систем автоматического регулирования.
Нарушение принципа суперпозиции в нелинейных системах, наличие целого ряда чередующихся
(в зависимости от воздействия) режимов устойчивого, неустойчивого движений и автоколебаний
затрудняют их анализ. Еще с большими трудностями встречается проектировщик при расчете
экстремальных и самонастраивающихся систем регулирования.
1.Устойчивость
линейной системы авторегулирования. Общие сведения
Устойчивость системы означает, что она принципиально
может выполнять свои функции. Для линейных систем можно пользоваться следующим определением
устойчивости: линейная система устойчива, если при ограниченном входном воздействии
выходной процесс тоже ограничен.
Прямым методом анализа устойчивости является решение
дифференциального уравнения, описывающего систему:
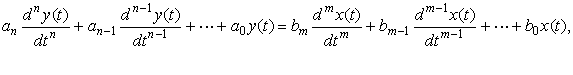
где  и
и 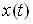 - соответственно выходной и
входной процессы в системе.
- соответственно выходной и
входной процессы в системе.
Устойчивость линейной системы не зависит от вида входного
воздействия, и можно взять его любым, в том числе и нулевым, но удобнее принять
x(t) = 1(t). В этом случае решением
дифференциального уравнения будет переходная характеристика. И по виду ее можно
определить устойчивость системы. Если переходная характеристика стремится к постоянному
значению, то система устойчива. Если же переходная характеристика уходит в бесконечность,
то неустойчива. Из решения дифференциального уравнения следует, что выходной процесс
ограничен, если корни характеристического уравнения располагаются в левой
полуплоскости.
anpn + an-1pn-1 +…+ a0 = 0
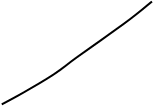
При анализе устойчивости систем авторегулирования
наиболее часто используется критерий устойчивости Найквиста. Согласно этому критерию
замкнутая система устойчива при устойчивой разомкнутой, если годограф частотной
характеристики разомкнутой системы не охватывает точки с координатами (-1, 0).Типовой
вид годографа частотной характеристики разомкнутой системы, описываемой передаточной
функцией
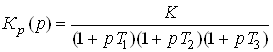 ,(3)
,(3)
Годограф начинается на действительной оси, так как
на нулевой частоте коэффициент передачи разомкнутой системы является действительной
величиной Кр(0) = К. С ростом частоты модуль коэффициента
передачи Кр(w) уменьшается и вносится отрицательный фазовый сдвиг
jр(w), поэтому вектор Кр(jw)
поворачивается по часовой стрелке. При w = ¥ Кр(w) = 0 и jр(w) = - 3p¤2. Для устойчивой системы
точка ( -1, 0) должна лежать вне фигуры, образованной годографом частотной характеристики
и действительной положительной полуосью.
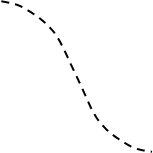
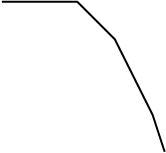
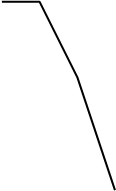
Если в разомкнутую систему входят интеграторы, то
годограф частотной характеристики разомкнутой системы начинается в бесконечности.
Такие системы называются астатическими. Количество интеграторов равно порядку астатизма.
Для системы с одним интегратором, имеющей передаточную функцию годограф
начинается в третьем квадранте (рис. 2), а для системы с двумя интеграторами с
передаточной функцией
 ,(4)
,(4)
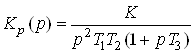 - (5)
- (5)
во втором квадранте, т.к. уже на нулевой частоте интегратор
вносит фазовый сдвиг, равный p¤2.
Для построения замкнутого контура в этих случаях требуется
к годографу добавить столько четвертей окружности бесконечного радиуса, сколько
интеграторов в разомкнутой системе. На рис. 2 и рис. 3 это добавление условно показано
пунктирной линией. Замкнутая система с годографом Кр(jw),
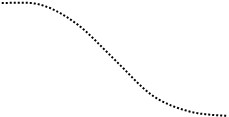
изображенном на рис. 2, устойчива, а на рис. 3 – неустойчива. Причем последняя является
структурно-неустойчивой, т.е. неустойчивой при любом коэффициенте передачи разомкнутой
системы.
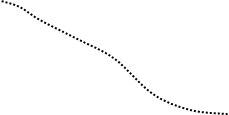
По годографу частотной характеристики разомкнутой
системы можно оценить степень устойчивости. Для этого вводится понятие запасов устойчивости
по усилению и по фазе. Запас устойчивости по усилению DК показывает, во сколько раз
нужно изменить коэффициент передачи разомкнутой системы, чтобы замкнутая из устойчивой
стала неустойчивой. Запас устойчивости по фазе Dj показывает, какой фазовый
сдвиг нужно ввести в разомкнутую систему, чтобы замкнутая из устойчивой стала неустойчивой.
На рис. 4 показано, как эти запасы определяются по годографу частотной характеристики
разомкнутой системы. Запас устойчивости по усилению DК = =1¤К1, где К1
– коэффициент передачи разомкнутой системы на частоте, для которой jр(w) = -p.Запас устойчивости по фазе
равен углу Dj между отрицательной действительной полуосью и линией,
соединяющей начало координат с точкой пересечения годографа с окружностью единичного
радиуса.
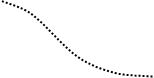
На практике удобнее пользоваться не годографом частотной
характеристики, а амплитудно-частотной и фазочастотной характеристиками. И еще более
удобно использовать логарифмические АЧХ и ФЧХ, т.е. ЛАХ и ЛФХ. Критерий Найквиста
в этом случае формулируется так: замкнутая линейная система устойчива при устойчивой
разомкнутой, если в области частот, где ЛАХ разомкнутой системы положительна, ЛФХ
разомкнутой системы или не пересекает значения -p, или пересекает его сверху
вниз и снизу вверх одинаковое количество раз. При монотонной ЛФХ разомкнутой системы
устойчивость можно определить, сравнивая две характерные частоты: частоту среза
wср, на которой ЛАХ пересекает ось частот, и критическую частоту wкр, на которой ЛФХ пересекает
значение -p. Для устойчивой системы wкр>wср. Запас устойчивости по усилению
DL определяется на критической частоте как расстояние от ЛАХ до оси
частот, а запас устойчивости по фазе – на частоте среза как расстояние от -p до ЛФХ (рис.5).
Логарифмические частотные характеристики позволяют
легко и наглядно исследовать влияние параметров системы на ее устойчивость. Рассмотрим
это на примере системы с передаточной функцией (3).
На рис. 6 изображены ЛАХ и ЛФХ разомкнутой системы
для следующих значений постоянных времени: Т1 = 10-1
с, Т2 = 10-2 с, Т3 = =10-3
с и различных значений коэффициента передачи К = 10; 100; 103.
При К = 10 замкнутая система устойчива. Запас устойчивости по фазе: 45 град,
по усилению: 20 дБ. При К= 100 система находится на грани устойчивости и
при К= 1000 неустойчива.
На рис.7 изображены логарифмические характеристики
разомкнутой системы при К = 100, Т2 = 10-2 с, Т3 = 10-3 с и различных значений Т1: 1 с; 0,1 с и 0,01 с. Видно,
что увеличение постоянной времени Т1 делает систему устойчивой и чем больше Т1, тем больше запасы устойчивости.
Уменьшение Т1 приведет к неустойчивости системы. Наиболее неблагоприятной будет
ситуация, когда все постоянные времени максимально близки друг к другу, т.е. при
Т1 = (Т2 + Т3) ¤ 2. При дальнейшем уменьше-
нии Т1 ЛФХ приподнимается в области частот, близких к частоте
среза, и склонность системы к неустойчивости будет уменьшаться. При Т1
= 0 ЛФХ не будет пересекать значения -p, и система будет
устойчивой при любом коэффициенте передачи.
Схема моделирования показана на рис. 8.
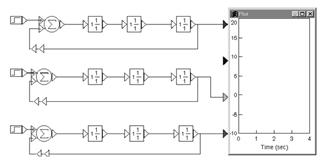
Рис.8
Исследование устойчивости для удобства сравнения проводится
на трех моделях, отличающихся структурой или параметрами.
2.Оптимальные линейные
САР
Задача оптимального синтеза линейной системы
авторегулирования при случайных воздействиях заключается в определении такой структуры
и параметров системы, при которых ошибки минимальны. Это так называемая задача оптимальной
линейной фильтрации. Она была решена Колмогоровым, Винером, Калманом. В постановке
Винера и Колмогорова входные процессы задаются их энергетическими спектрами. Для
САР входными процессами являются задающее xз(t) и возмущающее xв(t) воздействия
с энергетическими спектрами Sxз(w) и Sxв(w). Оптимальная частотная
характеристика без учета физической реализуемости системы имеет вид:
Копт(jw) = Sxз(w)/[Sxз(w) + Sxв(w)].
Объясняется такая форма частотной характеристики
просто. В области частот, где Sxв(w) = 0 АЧХ замкнутой системы равна 1, что и
требуется для безошибочного слежения. В области частот, занятых спектром возмущающего
воздействия, коэффициент передачи должен быть тем меньше, чем больше интенсивность
помехи.
Неудобство данного подхода для синтеза САР
заключается в том, что определяется только частотная характеристика замкнутой системы,
а структура системы неочевидна. В этом отношении удобнее подход Калмана, определяющий
структуру оптимальной системы. В отличие от предыдущего подхода, описывающего задающее
воздействие энергетическим спектром, в подходе Калмана задающее воздействие образуется
пропусканием белого шума через формирующий фильтр, который строится как устройство
с обратной связью. Формирующий фильтр описывается векторным дифференциальным уравнением,
которое называется уравнением состояния:
dXз(t)/dt = AXз(t) + Bn(t),
где n(t) – белый шум,
Xз(t) – вектор-столбец переменных состояния, которыми обычно являются сам
процесс xз(t) и его производные,
А – матрица системы,
В – матрица управления.
Для формирования задающего воздействия к уравнению
состояния добавляется уравнение наблюдения:
xз(t) = CXз(t),
где С – матрица наблюдения, устанавливающая
связь процесса xз(t) с вектором
переменных состояния Xз(t).
По этим уравнениям построена модель, представленная
на рис. 9. Сформированное таким образом задающее воздействие поступает на вход САР
вместе с возмущающим воздействием, которое считается белым шумом. Доказано, что
оптимальный фильтр Калмана повторяет структуру формирующего фильтра с точностью
до матричного коэффициента передачи К (рис. 10).Элементы матрицы К
и определяют оптимальность системы.
Проиллюстрируем сказанное на примере системы
первого порядка. Пусть в качестве формирующего фильтра используется интегрирующая
цепь с постоянной времени Тф. Ее передаточная функция: Кф(р)
= 1/(1 + рТф). Этой передаточной функции соответствует дифференциальное
уравнение в операторной форме:
(рТф + 1)xp(t) = n(t).
В обычной форме оно записывается так:
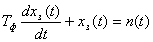 .
.
Отсюда
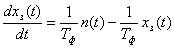 .
.
Модель, построенная по этому уравнению, изображена
на рис. 31
Оптимальная система представлена на рис. 12.
Оптимальное значение коэффициента передачи:
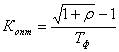 , (13)
, (13)
где r - отношение спектральных плотностей случайных процессов n(t) и xв(t).
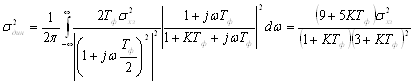
Дисперсия ошибки слежения в оптимальной системе:
 .(14)
.(14)
Рассмотрим ошибки в системе, отличающейся от
оптимальной. Отличие системы от оптимальной может заключаться как в отличии коэффициента
К от оптимального при оптимальной структуре системы, так и в неоптимальности
самой структуры.
Отличие коэффициента передачи К от оптимального
приведет к увеличению ошибки. Ошибка складывается из динамической ошибки и ошибки
по возмущению. Дисперсия динамической ошибки
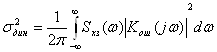 .
.
Спектральная плотность задающего воздействия
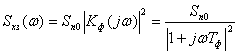 .
.
Дисперсия задающего воздействия
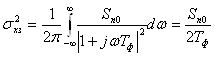 .
.
Выразим спектральную плотность Sn0 процесса n(t) через дисперсию задающего воздействия: Sn0 = 2Tфs2xз.
Частотная характеристика разомкнутой системы
для схемы, изображенной на рис. 32, имеет вид:

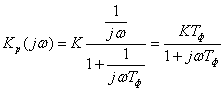 .
.
И соответственно,
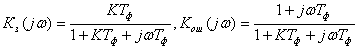 .
.
Тогда
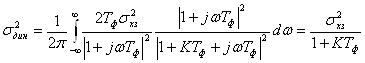 . (15)
. (15)
Для пояснения причины уменьшения динамической
ошибки с ростом коэффициента передачи К обратимся к рис. 13, на котором представлены
энергетический спектр процесса xз(t) (пунктирная линия) и АЧХ замкнутой системы при различных значениях
КТф (сплошные линии). Видим, что чем больше КТф,
тем меньше отличие коэффициента передачи замкнутой системы от 1 в области частот,
занятых спектром задающего воздействия.
Дисперсия ошибки по возмущению вычисляется
по формуле:
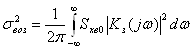 .
.
Так как спектральная плотность возмущающего
воздействия в r раз меньше спектральной
плотности Sn0, то
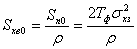
и
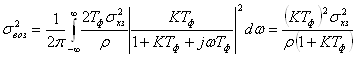 . (16)
. (16)
Дисперсия ошибки по возмущению увеличивается
с ростом КТф, так как увеличивается площадь под АЧХ замкнутой
системы. Зависимость дисперсии суммарной ошибки s2 = s2дин +
s2воз от
КТф показана на рис. 14 для различных значений r. Минимум достигается при оптимальном значении
коэффициента передачи. Следует отметить, что оптимум не очень критичен и при двукратном
отличии коэффициента передачи от оптимального дисперсия ошибки увеличивается на
15 – 20 %.
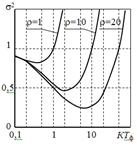
Рис.
Рассмотрим теперь, к какому увеличению дисперсии
приведет отличие структуры системы от оптимальной. Допустим, что система первого
порядка (рис. 32) осуществляет слежение за процессом xз(t), образованным
из белого шума формирующим фильтром второго порядка с пере-даточной функцией Кф(р)
= =1/(1 + рТф1)2. Подберем Тф1 так,
чтобы площади под |Кф(jw)½2 для
однозвенного и двухзвенного фильтров были одинаковыми. Тогда будет соблюдаться равенство
дисперсий выходных процессов обоих фильтров при одинаковой спектральной плотности
входного белого шума. Это условие выполняется при Тф1 = Тф/2.
На рис. 15 представлены АЧХ фильтров: однозвенного (сплошная линия) и двухзвенного
(пунктирная линия). Из-за отличия спектров задающего воздействия изменится динамическая
ошибка. Дисперсия динамической ошибки станет равной:
 .
.
Дисперсия ошибки по возмущению останется прежней,
так как частотная характеристика замкнутой системы не изменилась. На рис. 36 показано,
во сколько раз увеличивается минимальная дисперсия суммарной ошибки в системе с
неоптимальной структурой по сравнению с дисперсией ошибки в оптимальной системе
в зависимости от r.
Дисперсия ошибки в оптимальной системе рассчитана
по формуле:
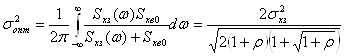 .
.
Исследуемая модель, содержащая формирующий
фильтр и оптимальную систему, приведена на рис. 17.
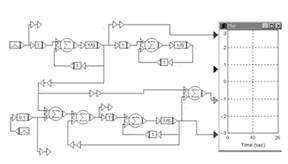
Рис. 17
В верхней части модели расположен формирующий
фильтр: одно- и двухзвенный, а в нижней части – оптимальная система для задающего
воздействия, сформированного однозвенным фильтром.
Заключение
Формирование систем
автоматического регулирования, как правило, выполняют на основе аналитических методов
анализа или синтеза. На этом этапе проектирования систем регулирования на основе
принятые допущений составляют математическую модель системы и выбирают предварительную
ее структуру. В зависимости от типа модели (линейная или нелинейная) выбирают метод
расчета для определения параметров, обеспечивающих заданные показатели устойчивости,
точности и качества. После этого уточняют математическую модель и с использованием
средств математического моделирования определяют динамические процессы в системе.
При действии различных входных сигналов снимают частотные характеристики и сравнивают
с расчетными. Затем окончательно устанавливают запасы устойчивости системы по фазе
и модулю и находят основные показатели качества.
Далее, задавая
на модель типовые управляющие воздействия; снимают характеристики точности. На основании
математического моделирования составляют технические требования на аппаратуру системы.
Из изготовленной аппаратуры собирают регулятор и передают его на полунатурное моделирование,
при котором объект регулирования набирают в виде математической модели.
Развитие теории
автоматического регулирования на основе уравнений состояния и z-преобразований,
принципа максимума и метода динамического программирования совершенствует методику
проектирования систем регулирования и позволяет создавать высокоэффективные автоматические
системы для самых различных отраслей народного хозяйства. Полученные таким образом
системы автоматического регулирования обеспечивают высокое качество выпускаемой
продукции, снижают ее себестоимость и увеличивают производительность труда.
Список литературы
1. Коновалов Г.Ф. Радиоавтоматика: Учебник для вузов. М.: Радиотехника,
2003. 288 с.
2. Первачев С.В. Радиоавтоматика: Учебник для вузов. М.: Радио
и связь, 1982. 296 с.
3. Радиоавтоматика: Учебное пособие / Под ред. В.А.Бесекерскогока: Учебник для вузов. М.: Радиотехника,
2003. 288 с.
2. Первачев С.В. Радиоавтоматика: Учебник для вузов. М.: Радио
и связь, 1982. 296 с.
3. Радиоавтоматика: Учебное пособие / Под ред. В.А.Бесекерского.
М.: Высшая школа, 1985.271 с.
4. Системы радиоавтоматики и их модели: Учеб. пособие / Ю.Н.Гришаев;
Рязан. радиотехн. институт. Рязань, 1977. 46 с.
5. Шахгильдян В.В., Ляховкин А.А. Системы фазовой автоподстройки
частоты. М.: Связь, 1972.448 с.
6. Синтез частотных характеристик линейных систем автоматического
регулирования: Метод. указания / Рязан. гос. Радиотехн.акад.; Сост. Ю.Н.Гришаев.
Рязань, 2000. 12 с.
автоматический регулирование линейный система
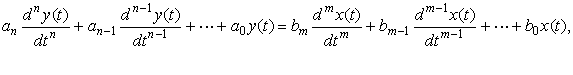
![]() и
и ![]() - соответственно выходной и
входной процессы в системе.
- соответственно выходной и
входной процессы в системе.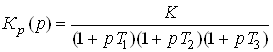 ,(3)
,(3)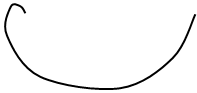
 ,(4)
,(4)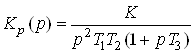 - (5)
- (5)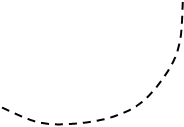













![]() .
.![]() .
.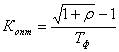 , (13)
, (13)
 .(14)
.(14)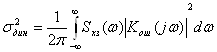 .
.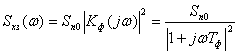 .
.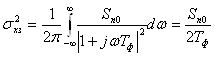 .
.![]()
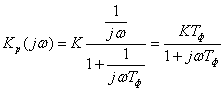 .
.![]() .
.![]()
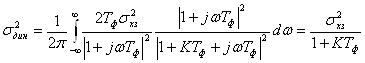 . (15)
. (15)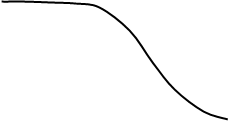

![]() .
.![]()
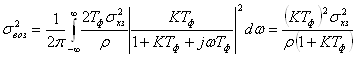 . (16)
. (16)
 .
.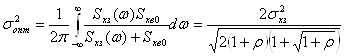 .
.