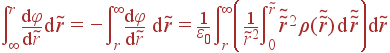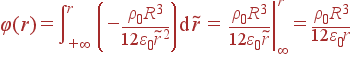Статья: Уравнение Пуассона. Его применение для расчета полей в вакууме
М.И. Векслер, Г.Г. Зегря
Уравнение Пуассона для ε = 1 выглядит:
|
|
(16) |
Это уравнение - основа практических численных расчетов.
В задачах, решаемых аналитически, φ и ρ обычно зависят только от одной координаты. При интегрировании можно вычислять интегралы как неопределенные, не забывая выписывать +const, а затем отдельно находить эти константы. Если раccматриваются отдельные диапазоны координат, то на незаряженных границах необходимо "сшивать" потенциал: φ и - для вакуума - d φ/dx (или dφ/dr) не должны иметь разрыва. Если граница заряжена (σ), то dφ/dx испытывает скачок на величину –σ/ε0. Кроме того, если ρ и суммарный заряд конечны, то φ всюду конечен.
Другой
вариант - сразу правильно писать пределы интегрирования. Для этого используется
известное (или очевидное из симметрии задачи) значение поля (![]() ) в
одной какой-либо точке и значение потенциала в какой-либо точке (не обязательно
в той же, где знаем поле). Если в задаче не оговорено иное, то следует
принимать φ|∞ = 0. Так, например, для случая зависимости потенциала
только от одной сферической координаты r
) в
одной какой-либо точке и значение потенциала в какой-либо точке (не обязательно
в той же, где знаем поле). Если в задаче не оговорено иное, то следует
принимать φ|∞ = 0. Так, например, для случая зависимости потенциала
только от одной сферической координаты r
|
|
(17) |
после переноса r2 в правую часть и двух последовательных интегрирований получаем:
|
|
= |
|
(18) |
| φ(r) | = |
|
(19) |
При этом взято φ|r = ∞ = 0 и учтено то обстоятельство, что при всюду конечном ρ поле в центре равно нулю (–dφ/dr|r = 0 = 0).
Задача. Пластина ширины 2a (ее ε≈ 1) заряжена равномерно по объему (ρ(x) = ρ0); при x = 0 (центр пластины) φ = 0. Найти φ(x).
Ответ:
![]() , |x|<a;
, |x|<a; ![]() ,
|x|>a
,
|x|>a
|
|
Задача. Пластина ширины 2a (ее ε≈ 1) заряжена как ρ(x) = α x2; при x = 0 (центр пластины) φ = 0. Найти φ(x).
Решение: Мы работаем в декартовой системе координат, причем очевидно, что и поле, и потенциал зависят только от x. Если ρ>0 (α >0) то поле - из симметрии задачи - направлено по оси x при x>0 и против оси x при x<0. Согласно уравнению Пуассона:
|
|
= |
|
|
|
|
= | 0 x>a или x<–a |
После первого интегрирования (интеграл берем как неопределенный)
|
|
= |
|
|
|
|
= | AL, x<–a | |
|
|
= | AR, x>a |
Неверным было бы записать одну общую константу для dφ /dx при x>a и x<–a. Второе интегрирование дает:
| φ(x) | = |
|
|
| φ(x) | = | ALx+BL, x<–a | |
| φ(x) | = | ARx+BR, x>a |
Для нахождения шести констант у нас есть четыре условия сшивания (по два для границ x = –a и x = a). Кроме того, дано указание взять φ(0) = 0. Видно также, что Ex|x = 0 = –dφ/ dx|x = 0 = 0. Последнее очевидно из симметрии задачи. Отсюда сразу
| Ac = 0, Bc = 0 |
Из симметрии следует также, что φ(x) = φ(–x) и что Ex(x) = –Ex(–x), вследствие чего
| AR = –AL, BR = BL |
Это делает достаточным рассмотрение условий сшивания только на одной из границ, например при x = a:
|
|
= | (ARx+BR)|x = a | |
|
|
= | AR|x = a |
Сначала получаем AR (AR = –α a3/3ε0), а затем BR (BR = α a4/4ε0), после чего остается выписать ответ:
| φ(x) | = |
|
|
| φ(x) | = |
|
|
| φ(x) | = |
|
Альтернативой было бы интегрирование с выписыванием пределов сразу:
| Ex(x) | = |
|
|
| φ | = |
|
Такое интегрирование верно всегда, в том числе при x<0. Точки x = ± a при этом ничем не выделены, но надо помнить, что вне участка –a<x<a ρ = 0 и учитывать это при подстановке плотности заряда в выражение для интеграла. После взятия интеграла в таком виде сшивание потенциала не требуется.
|
|
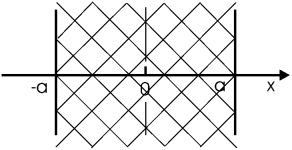
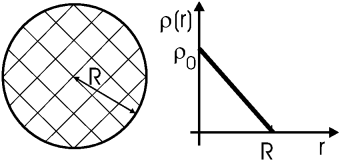
Задача. Шар радиуса R заряжен как ρ(r) = ρ0(1–r/R). Найти полный заряд шара Q, поле Er(r), а также потенциал φ(r) при r = 0... +∞.
Решение: Полный заряд шара находится как
| Q | = |
|
|
| = |
|
При вычислении мы использовали выражение для элемента объема dV в сферических координатах (не следует смешивать фигурирующий при этом φ с обозначением потенциала). Уравнение Пуассона записывается:
|
|
= |
|
Поcле однократного интегрирования в пределах 0... r имеем
|
|
= |
|
|
| = |
|
Заметим,
что - с точностью до знака - мы уже получили поле, поскольку ![]() . Для нахождения потенциала
φ(r) требуется повторное интегрирование:
. Для нахождения потенциала
φ(r) требуется повторное интегрирование:
| r>R | : |
|
|
| r<R | : |
|
|
| = |
|
Список литературы
1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.
2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.
3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.: Наука, 1992. - 661 с.
Для подготовки данной работы были использованы материалы с сайта http://edu.ioffe.ru/r
| Курс лекций по теории вероятностей | |
|
Раздел 1. Классическая вероятностная схема 1.1 Основные формулы комбинаторики В данном разделе мы займемся подсчетом числа "шансов". О числе шансов ... 1. Точка с координатами ѭ, ѭ бросается наудачу в квадрат со стороной 1. Доказать, что для любых х, у R события A = { ѭ <x} и B= { ѭ <y} независимы. Пусть х R, и область Dx R2 состоит из точек (x1 x2 ) таких, что g (x1 x2 ) < x. Тогда случайная величина ѭ = g(ѭ1 , ѭ2). имеет функцию распределения |
Раздел: Рефераты по математике Тип: реферат |
| Ряды Фурье и их приложения | |
|
Министерство общего и профессионального образования Сочинский государственный университет туризма и курортного дела Педагогический институт ... Из доказанного свойства вытекает, что при вычислении коэффициентов Фурье мы можем заменить промежуток интегрирования (-ѭ, ѭ) промежутком интегрирования (ѭ, ѭ +2ѭ), т. е. можем ... Электрический ток в проводе характеризуется величиной ѭ(x, t) и напряжением ѭ(x, t), которые зависят от координаты х точки провода и от времени t. Рассматривая элемент провода =х ... |
Раздел: Рефераты по математике Тип: реферат |
| Шпора | |
|
Билет №1 Пусть в обл. P плоскости XOY задана некоторая фун-ия z=f(x;y). Разобъём обл. P на n частичных обл. Рi , где i=1.n, возмём произвольную точку ... P плоскости XOY задана некоторая фун-ия z=f(x;y). Разобъём обл. Если же функция f(x;y) такова, что существует двойной интеграл по области R, существуют оба од- номерных J(y) и Ѭ(x), то одновременно имеют место формулы (1) и (2) D на части и выбора точек (xi,yi,zi) , то этот предел называют тройным интегралом по обл.D от ф-ции f(x,y,z) lim( n= f(x,y,z)dx dy dz Следовательно m= (x,y,z)dxdydz |
Раздел: Рефераты по математике Тип: реферат |
| Исследование движения центра масс межпланетных космических аппаратов | |
|
2. ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ 2.1. ВВЕДЕНИЕ В данной работе проводится исследование движения центра масс МКА под действием различных возмущающих ... Чтобы найти возмущающее ускорение от нецентральности поля тяготения Земли в проекциях на оси абсолютной системы координат OXYZ, надо взять производные от возмущающего потенциала Uв ... После интегрирования мы получаем вектор состояния КА (x, y, z, Vx, Vy, Vz) в любой момент времени. |
Раздел: Рефераты по астрономии Тип: реферат |
| Физические модели при изучении интеграла в курсе алгебры и начал ... | |
|
Содержание. Введение Глава1. Теоретические основы изучения темы "Интеграл" с помощью моделей 1.1. Модели и моделирование в обучении 1.2. Психолого ... При рассмотрении понятия интеграла в школах с углубленным изучением математики возможно также и обучение простейшим методам интегрирования (технике вычисления интеграла). Покажем, что координата центра масс равна .Разобьем отрезок [a; b] на n равных частей точками a=x0<x1<.<xn=b. На каждом из n этих отрезков плотность можно считать при больших n ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |